Pythagorean模糊環(huán)境下基于交叉熵和TOPSIS的多準(zhǔn)則決策方法

范建平，閆 彥，吳美琴

FAN Jianping,YAN Yan,WU Meiqin

山西大學(xué) 經(jīng)濟(jì)與管理學(xué)院，太原 030006

School of Economics and Management,Shanxi University,Taiyuan 030006,China

1 引言

隨著參與人數(shù)的增加，決策速度變得更緩慢，決策過程也變得更復(fù)雜。因而多屬性群決策在現(xiàn)代決策理論和決策科學(xué)中發(fā)展為一個極為重要的研究領(lǐng)域，在工程、物流、醫(yī)學(xué)及軍事等諸多方面都有著廣泛的應(yīng)用。Zadeh提出用隸屬度表示決策信息的不確定性和模糊性，模糊集[1]（Fuzzy Set，F(xiàn)S）理論迅速發(fā)展起來。然而僅僅通過隸屬度描述不確定性是不夠的，因此Atanassov等提出同時用非隸屬度和猶豫度的概念來表達(dá)決策信息的模糊性和不確定性，將其擴(kuò)展到了直覺模糊集[2]（Intuitionistic Fuzzy Set，IFS）理論。隨后Gau和Buehrer定義了Vague集[3]。Torra等[4-5]提出猶豫模糊集（Hesitant Fuzzy Set，HFS）的概念，允許隸屬度可以以多個可能值集合的形式存在，用來表達(dá)專家在決策過程中表達(dá)目標(biāo)偏好時的猶豫程度。雖然模糊集已經(jīng)發(fā)展很廣泛，但仍然無法解決隸屬度和非隸屬度之和大于等于1的情況。比如，一位專家表達(dá)他認(rèn)為方案滿足某準(zhǔn)則的程度是0.8，不滿足程度是0.4。這種情況就無法用直覺模糊集解決。因此，Yager[6]提出Pythagorean模糊集（Pythagorean Fuzzy Set，PFS），擴(kuò)大了隸屬度和非隸屬度的空間范圍，即拓展到隸屬度與非隸屬度平方之和小于等于1。Pythagorean隸屬度和復(fù)數(shù)之間的關(guān)系也很好地被Yager和Abbasov[7]討論，并證明Pythagorean隸屬度是復(fù)數(shù)的一個子集，稱作π-i數(shù)，并提出集結(jié)算子對準(zhǔn)則滿意度進(jìn)行集結(jié)。

各位學(xué)者將不同的方法引入PFS中。Ren等[8]基于前景理論，將TODIM方法運用在Pythagorean模糊集中，并分析了風(fēng)險如何影響心理行為。Zhang[9]在多準(zhǔn)則Pythagorean模糊環(huán)境下提出一個分層的QUALIFLEX方法，并用貼近度索引排名法對Pythagorean模糊數(shù)（Pythagorean Fuzzy Number，PFN）進(jìn)行排名，同時提出區(qū)間PFS的概念。Garg[10]提出一個新的相關(guān)系數(shù)和加權(quán)相關(guān)系數(shù)公式來計算兩個Pythagorean模糊集的關(guān)系，并用在模式識別和醫(yī)療診斷。Garg[11]在解決多準(zhǔn)則決策問題時基于區(qū)間Pythagorean模糊環(huán)境提出了一個新的精確函數(shù)，它考慮到了未知的猶豫度。Zhang[12]提出了一個新的基于相似度測量的方法來解決基于PFN的多準(zhǔn)則群決策問題。Peng等[13]定義了兩個新的運算，除法和減法，并對其性質(zhì)深入研究，也拓展了一個Pythagorean模糊優(yōu)勢和劣勢排序法來解決多準(zhǔn)則不確定群決策問題。Peng等[14]將PFS的特征和軟集的參數(shù)化相結(jié)合構(gòu)造了畢達(dá)哥拉斯模糊軟集，并對其德摩根定律進(jìn)行討論，還設(shè)計了基于Pythagorean模糊整合算子的決策算法，并對其計算復(fù)雜度進(jìn)行了分析。Gou等[15]對Pythagorean模糊信息的一些基本性質(zhì)進(jìn)行研究，把PFN看作變量，并根據(jù)其基本運算把所有變化的值分為8個區(qū)域，同時對其基本性質(zhì)中的連續(xù)性、可導(dǎo)性和可微性進(jìn)行詳細(xì)探討。

為了對決策信息進(jìn)行集結(jié)，Ma等[16]、Peng 等[17]、Garg[18]和 Peng 等[19]基于對稱性、Choquet積分、Einstein運算和語言集分別提出了對應(yīng)的集結(jié)算子。Peng等[20]提出了區(qū)間Pythagorean模糊加權(quán)平均（IVPFWA）算子和區(qū)間Pythagorean模糊加權(quán)幾何（IVPFWG）算子，以及一個新的區(qū)間Pythagorean模糊ELECTRE方法來解決不確定多屬性群決策問題。Peng等[21]提出了幾個新的Pythagorean模糊點集結(jié)算子，可以根據(jù)某些參數(shù)調(diào)整集結(jié)信息的大小。Zeng等[22]提出了新的集結(jié)算子和距離測度，在集結(jié)算子中使用了距離測度，同時考慮到了每個概念的重要程度，并提出了一個混合的TOPSIS方法來解決Pythagorean模糊多準(zhǔn)則決策問題。

基于Luca等[23]提出的模糊熵概念，Bhandari等[24]在模糊集中通過隸屬函數(shù)定義了交叉熵。最大交叉熵原理[25]可以被用來從大數(shù)據(jù)庫中選擇有代表性的樣本，被用在機(jī)器學(xué)習(xí)和決策樹中。Mao等[26]基于直覺模糊集提出了一個新穎的交叉熵和熵測度，并將其應(yīng)用到模式識別和決策中。

Zhang等[27]將TOPSIS擴(kuò)展到了PFS中，并基于PFN定義了得分函數(shù)和距離的概念。首先提出得分函數(shù)來確認(rèn)Pythagorean模糊正理想解和負(fù)理想解，同時定義了兩個PFN之間的距離，采取了歐氏距離的表示形式，但是根據(jù)所定義的距離對PFN進(jìn)行集結(jié)時會忽略掉一些模糊信息。因此，本文定義了兩個PFN之間的交叉熵，并采用交叉熵來測定它們之間的“距離”，以此消除在距離測度中使用歐氏距離引起的不確定性，可以更大程度地保留不確定信息。本文主要在TOPSIS原理的基礎(chǔ)上，采取交叉熵描述兩個PFN之間的差異程度，最終通過每個方案和正、負(fù)理想解之間的相對貼近度來選出最優(yōu)的方案。本文最主要的創(chuàng)新之處便是將交叉熵概念引入Pythagorean模糊集中，并提出了兩個Pythagorean模糊集交叉熵測度。最后通過算例，以及與其他文獻(xiàn)中所提方法的比較分析驗證了本文方法的有效性。

2 相關(guān)概念

2.1 Pythagorean模糊集

定義1[7]設(shè)X是一個非空集合，則X中任意的Pythagorean模糊集P表達(dá)如下：

函數(shù)μP(x)和νP(x)分別表示集合P中元素x∈X的隸屬度和非隸屬度，滿足約束條件表示元素x屬于P的猶豫度（不確定程度），πp(x)的值越小說明關(guān)于x的信息越多，也越為精確；反之亦然。

為了簡便，PFS的元素(μP(x),νP(x))稱作一個Pythagorean模糊數(shù)[27]，記為γ=P(μP,νP)，其猶豫度同樣滿足

定義2[27]P的補集定義為PC,PC={＜x,νP(x),μP(x)＞|x∈X}。

定義3[6]γ1=P(μP1,νP1) 和γ2=P(μP2,νP2) 是 兩 個PFN，二者之間的一個擬排序定義如下：

γ1≥γ2當(dāng)且僅當(dāng)μP1≥μP2且νP1≤νP2

定義4[27]記γ=P(μP,νP)是一個PFS，則γ的得分函數(shù)定義如下：

定義5[11]一個PFN記作γ=P(μP,νP)，則γ的精確函數(shù)定義如下：

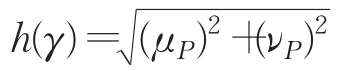
γ1=P(μP1,νP1)，γ2=P(μP2,νP2)，可分別根據(jù)二者的得分函數(shù)和精確函數(shù)對其比較大小，方法如下：

（1）若S(γ1)＞S(γ2)，則γ1＞γ2。

（2）若S(γ1)=S(γ2)，則：

① 若h(γ1)＞h(γ2)，則γ1＞γ2；

② 若h(γ1)=h(γ2)，則γ1=γ2；

③ 若h(γ1)＜h(γ2)，則γ1＜γ2。

2.2 TOPSIS方法

在Pythagorean模糊環(huán)境下根據(jù)TOPSIS原理，定義Pythagorean模糊正理想解（PIS）和Pythagorean模糊負(fù)理想解（NIS）[27]。TOPSIS的原則是最優(yōu)方案應(yīng)該與正理想解PIS有著最小距離，同時與負(fù)理想解NIS有著最大距離。考慮到?jīng)Q策信息采取PFN的格式，因此使用定義4中得分函數(shù)來確定Pythagorean模糊PIS和Pythagorean模糊NIS。將Pythagorean模糊PIS[27]定義為x+，并且具有下列形式：

在實際的多準(zhǔn)則決策問題中，并不一定存在Pythagorean模糊PIS，即x+并非可行的方案，不滿足x+∈X。反之x+就是多準(zhǔn)則決策問題中的最優(yōu)方案。然而，方案與x+有最短距離并不能保證與Pythagorean模糊負(fù)理想解（NIS）有最大距離。定義Pythagorean模糊NIS[27]為x-，表達(dá)如下：

同樣，通常在實際的多準(zhǔn)則決策問題中，也不一定存在x-，即x-也許是一個非可行方案，x-∈X。否則，x-在多準(zhǔn)則決策問題中就應(yīng)該是最差的方案，在決策過程中應(yīng)該首先被剔除。

2.3 Pythagorean模糊交叉熵

基于模糊集交叉熵的定義，本文提出兩個PFS的交叉熵定義。

定義7 設(shè)A、B為兩個PFS，A=(μA(xi),νA(xi)),B=(μB(xi),νB(xi))，則A、B之間的Pythagorean模糊交叉熵IPFS(A,B)定義為：

式（3）和式（4）中，IPFS(A,B)均說明了A、B之間的差異程度，也稱為兩個PFS之間包含的差異信息。因為IPFS(A,B)均不具有對稱性，所以A、B之間的對稱差異測度表示為：

定義6[24]設(shè)A、B是兩個模糊集，X={x1,x2,…,xn}是一個有限論域，A,B∈X，則A相對于B的交叉熵為：

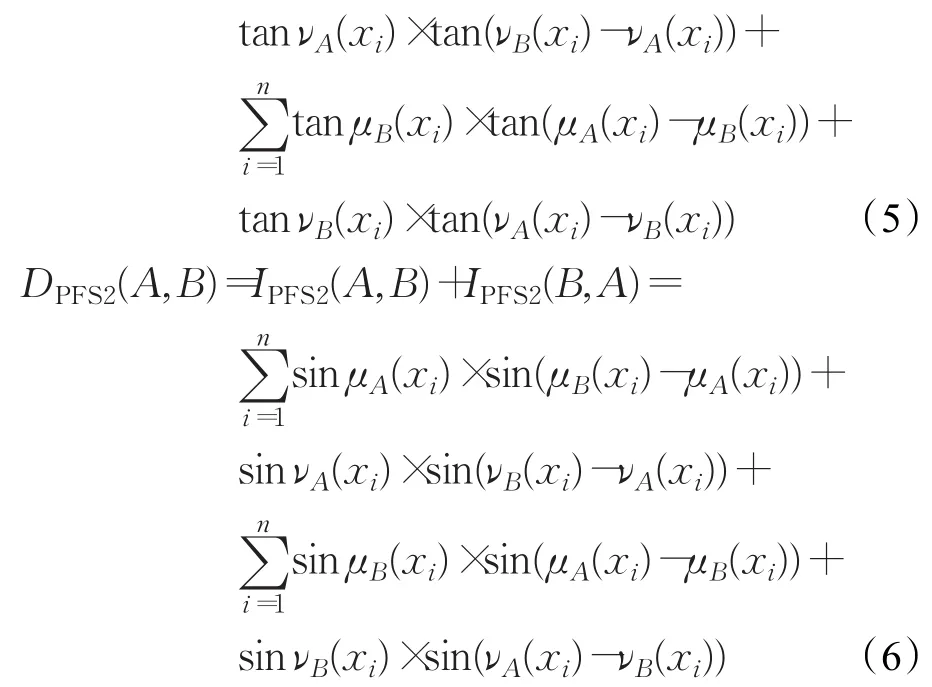
DPFS(A,B)稱為兩個PFS的對稱差異信息測度。

定理1A、B是兩個PFS，將A、B之間的對稱差異信息測度定義為DPFS(A,B)，則下列定理成立：

（1）DPFN1(A,B)=DPFN1(B,A)且

DPFN2(A,B)=DPFN2(B,A)；

（2）DPFN1(A,B)=DPFN1(AC,BC)且

DPFN2(A,B)=DPFN2(AC,BC)，AC和BC分別是A和B的補集，見定義2；

（3）DPFN1(A,B)≥0（DPFN1(A,B)=0當(dāng)且僅當(dāng)A=B)，DPFN2(A,B)同樣成立；

（4）A、B之間區(qū)別越大，則DPFN1(A,B)、DPFN2(A,B)越大。

證明 很顯然定理中（1）和（2）是成立的，（3）和（4）的證明如下。

首先證明定理（3）。考慮等式（7）：

x∈[0,1]且y∈[0,1]。顯然不論x≥y或y≥x，函數(shù)f1(x,y)≥0總是成立。

根據(jù)交叉熵公式（5），下列公式可以得到：

因為 ?(μA(xi),μB(xi),νA(xi),νB(xi))∈[0,1],且由式（7）有f1(x,y)≥0，所以 (tanμA(xi)-tanμB(xi))×tan(μA(xi)-μB(xi))≥0,(tanνA(xi)-tanνB(xi))×tan(νA(xi)-νB(xi))≥0。則有DPFS1(A,B)≥0成立。尤其是DPFS1(A,B)=0成立當(dāng)且僅當(dāng)μA(xi)=μB(xi)，νA(xi)=νB(xi)，即A=B。

然后證明定理（4）。A=(μA,νA)，B=(μB,νB)和C=(μC,νC)是3個PFS。假設(shè)A≥B≥C，根據(jù)定義3有，μA≥μB≥μC，νA≤νB≤νC，由式（8）可得：

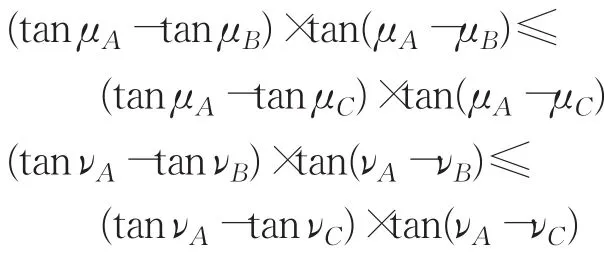
此外，容易得到下列不等式是正確的。顯然，DPFS1(A,C)≥DPFS1(A,B)成立。同樣可證明DPFS1(A,C)≥DPFS1(B,C)成立。

同理可證DPFS2，此處略。

3 模型構(gòu)建

多準(zhǔn)則決策問題可通過一個決策矩陣來表達(dá)，它的元素即每個方案在每個準(zhǔn)則下的估計值。現(xiàn)考慮一個Pythagorean模糊環(huán)境下的多準(zhǔn)則決策問題，X={x1,x2,…,xm}(m≥2)是m個方案的集合，C={C1,C2,…,Cn}是n個準(zhǔn)則的決策準(zhǔn)則集，W=(w1,w2,…,wn)T是所有準(zhǔn)則對應(yīng)的權(quán)重向量，滿足0≤wj≤1且現(xiàn)在定義方案xi(i=1,2,…,m)在準(zhǔn)則Cj(j=1,2,…,n)下的估計值為Cj(xi)=(uij,vij)，則R=(Cj(xi))m×n就是一個Pythagorean模糊決策矩陣。因此，元素是PFN的多準(zhǔn)則決策問題有如下的矩陣形式：

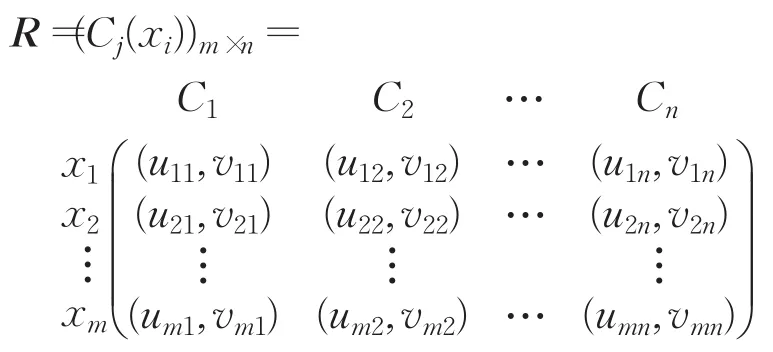
矩陣中的每一個元素Cj(xi)=P(uij,vij)是一個PFN，uij表示方案xi滿足準(zhǔn)則Cj的值，vij表示方案xi不滿足準(zhǔn)則Cj的值。

為了有效求解包含PFN的多準(zhǔn)則決策問題，本文提出一個Pythagorean模糊環(huán)境下基于交叉熵和TOPSIS方法，具體步驟如下：

步驟1標(biāo)準(zhǔn)化決策矩陣。

決策矩陣R中決策信息Cj(xi)必須是標(biāo)準(zhǔn)化后的。對于一個元素是PFN的多準(zhǔn)則決策問題，先建立決策矩陣元素是Cj(xi)(i=1,2,…,m,j=1,2,…,n)，表示方案xi∈X在準(zhǔn)則Cj∈C下的評估值。準(zhǔn)則可以分為成本準(zhǔn)則和效益準(zhǔn)則，可以根據(jù)下列公式標(biāo)準(zhǔn)化決策信息：

B是效益型的準(zhǔn)則集，C是成本型的準(zhǔn)則集，的補集。標(biāo)準(zhǔn)化后的矩陣為：

R=(Cj(xi))m×n

步驟2計算x+和x-。

根據(jù)式（1）和式（2）確定Pythagorean模糊正理想解x+和負(fù)理想解x-。

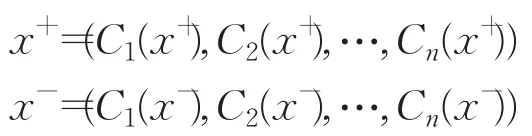
步驟3計算方案xi和x+以及x-之間的交叉熵。

根據(jù)式（5）和式（6）分別計算第i個方案xi與Pythagorean模糊正理想解x+和負(fù)理想解x-之間的交叉熵，以xi和x+以及x-之間的交叉熵分別來替代xi和x+與x-之間的距離。

步驟4計算方案xi的相對貼近度。

基于TOPSIS原理計算方案xi的相對貼近度[8]，記為ζ(xi)(i=1,2,…,m)，其計算公式如下：

步驟5確定最優(yōu)方案。

ζ(xi)越大，則方案越優(yōu)；反之亦然。基于所有方案的最優(yōu)順序確定最優(yōu)方案。

4 算例分析

算例是一個綠色供應(yīng)商的選擇問題。有5個待選的綠色供應(yīng)商X={x1,x2,x3,x4,x5}，6個準(zhǔn)則C={C1,C2,C3,C4,C5,C6}，分別代表“產(chǎn)品質(zhì)量”、“柔性”、“安全因素”、“服務(wù)”和“提前期”，以選出最優(yōu)的綠色供應(yīng)商。表1是其Pythagorean模糊決策表，表內(nèi)每一個元素分別代表該供應(yīng)商在相對應(yīng)準(zhǔn)則下的評價值，用PFN的形式表示，相對于決策矩陣的權(quán)重向量為W=(0.20,0.10,0.30,0.15,0.15,0.10）T。

步驟1標(biāo)準(zhǔn)化決策矩陣。

因為準(zhǔn)則都是效益型準(zhǔn)則，所以決策矩陣不變。

步驟2計算x+和x-。

根據(jù)式（1）和式（2）計算x+、x-，結(jié)果如下：

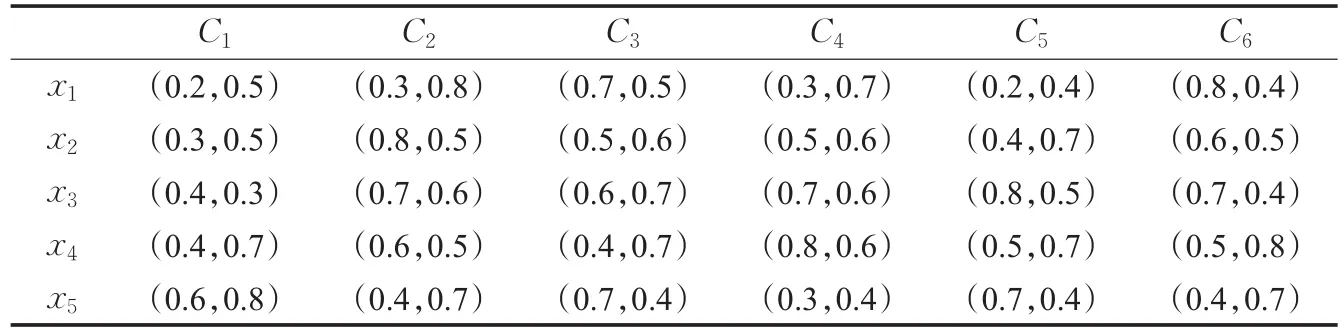
表1 Pythagorean模糊決策矩陣

步驟3根據(jù)式（5）中DPFS1(A,B)計算供應(yīng)商xi分別與x+和x-之間的交叉熵，結(jié)果見表2；根據(jù)式（6）中DPFS2(A,B)計算供應(yīng)商xi分別與x+和x-之間的交叉熵，結(jié)果見表3。

表2 由本文交叉熵DPFS1(A,B)得到的結(jié)果

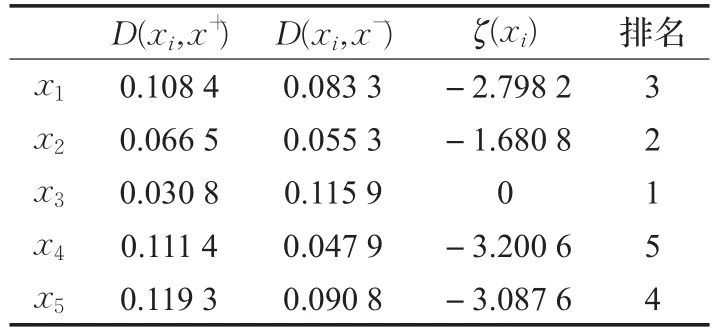
表3 由本文交叉熵DPFS2(A,B)得到的結(jié)果

步驟4由式（9）分別計算供應(yīng)商xi的相對貼近度ζ(xi)，結(jié)果見表2和表3。

步驟5根據(jù)相對貼近度選出最優(yōu)的綠色供應(yīng)商。由表2得4個供應(yīng)商的排序為：

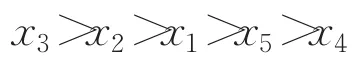
因此最優(yōu)的供應(yīng)商是x3，最劣的供應(yīng)商是x4。

表4是本文所提的方法（有序數(shù)對分別為各方案與正、負(fù)理想解的交叉熵，根據(jù)相對貼近度進(jìn)行排序）和文獻(xiàn)[27]中TOPSIS法（有序數(shù)對分別為各方案與正、負(fù)理想解的距離，根據(jù)相對貼近度進(jìn)行排序）和文獻(xiàn)[6]（有序數(shù)對分別為各方案經(jīng)過算子集結(jié)后的結(jié)果，根據(jù)得分函數(shù)進(jìn)行排序）中提出的兩個集結(jié)算子以及文獻(xiàn)[26]中提出的交叉熵計算結(jié)果的比較。為了更形象、直觀地表示各方案的排名結(jié)果，包括TOPSIS方法、PFWA算子、PFWG算子以及本文提出的交叉熵1和2，將所有結(jié)果繪于圖1。與已有方法的排名結(jié)果相比較，最優(yōu)供應(yīng)商是一樣的，都是x3，其他方案之間的排名有偏差，但是兩個交叉熵公式結(jié)果對于最優(yōu)方案和最劣方案的一致性驗證了其穩(wěn)定性和可行性。與文獻(xiàn)[27]中的TOPSIS方法相比較，文獻(xiàn)[27]計算兩個PFS之間的“距離”時采用簡單的歐幾里德距離，會丟失掉一些不確定信息，本文方法采用交叉熵對PFS之間進(jìn)行差異測度，考慮到評價過程中信息具有的模糊性和評價準(zhǔn)則之間的關(guān)聯(lián)，消除了歐氏距離帶來的不確定性，是一個較為合適的不確定信息和不連續(xù)信息測量。

表4 對于算例不同方法的計算結(jié)果

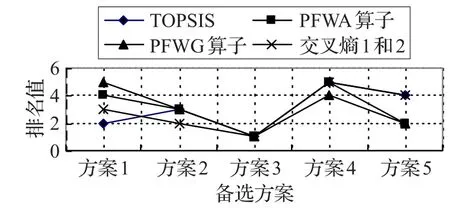
圖1 5種方法的比較結(jié)果

5 結(jié)語

Pythagorean模糊集由于比直覺模糊集有更廣闊的范圍，因此可以被用于解決現(xiàn)實中直覺模糊集所不能解決的包含不確定、不完整和不一致信息的問題。本文的主要貢獻(xiàn)如下：（1）在一般的TOPSIS方法中，采用歐氏距離測度，本文用交叉熵替代其中的距離測度，使其決策過程中包含的不確定信息更加完整，具有較高的準(zhǔn)確性，同時減少了因為采用的測度不確定性而帶來的誤差。（2）本文將直覺模糊環(huán)境下的基于交叉熵與TOPSIS的方法拓展運用在Pythagorean模糊環(huán)境下，并提出Pythagorean模糊集中交叉熵的概念，同時提出兩個交叉熵公式，豐富了Pythagorean模糊集的研究。最后，基于相同算例下本文方法和其他不同方法得到結(jié)果的比較分析也表明了本文方法的有效性和應(yīng)用性。

未來，根據(jù)實際應(yīng)用領(lǐng)域的不同需求，可以對Pythagorean模糊集中的交叉熵的形式以及應(yīng)用范圍進(jìn)行更多的研究。