在數學解題中培養學生的元認知能力

黃銀色

[摘 要] 高元認知能力者解決問題的能力明顯高于低元認知能力者，在數學解題上則表現得更為突出. 解題教學的目的不是純粹為了教會學生解幾道題或幾類題，而是要讓學生在解題的實踐中獲得題感，再從題感中提煉和升華數學思想方法，最終內化成學生的一種元認知能力.

[關鍵詞] 數學解題；元認知能力；調節；監控；完善

數學元認知能力是指學生在數學學習，特別是在數學解題活動過程中，對數學認知過程的自我意識、自我監控、自我調節的能力. 它以元認知知識和元認知體驗為基礎，并在數學認知活動過程中起指導、支配、決策、監控、調節的作用.

元認知理論告訴我們，有較強數學元認知能力的學生，在數學解題時，一方面能充分認識自身的知識水平、能力水平、智力水平、認知方式等，能對當前數學問題的結構特征、呈現方式、知識要求、任務目標等有較清晰的認識和預見，另一方面又懂得根據當前數學問題隨機應變，自主計劃、主動監控、自如調節，以最優化的思路、方法、路徑去實現解題目標. 有研究資料表明，高元認知能力者解決問題的能力明顯高于低元認知能力者，在數學解題上則表現得更為突出.

根據波利亞的《怎樣解題》，數學解題的一般步驟為：弄清問題、擬訂計劃、實施計劃、回顧解題. 本文將通過例題，淺談在解題的各個階段中該如何培養學生的元認知能力.

案例

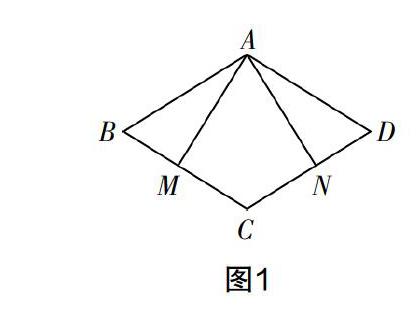
如圖1，在四邊形ABCD中，AD∥BC， AM⊥BC，垂足為M，AN⊥DC，垂足為N. 若∠BAD=∠BCD， AM=AN，求證四邊形ABCD是菱形.

1. 弄清問題

學生讀題后，教師提示：

（1）題目的條件和目標分別是什么？

（2）根據每一個條件思考給出此條件的目的是什么？

（3）是否明確了要完成的任務？

若老師能經常用這些提示語啟發和引導學生思考并逐漸將這些知識內化為學生的自覺行動，幫助學生養成了元認知習慣，往往能打破思維的僵局，找到解決問題的切入點或突破口.

2. 擬訂計劃

提示1：要實現目標，有幾種解決目標的方法？它們都是什么？

要證明一個四邊形是菱形，學生必須在頭腦中構建一個菱形判定方法的知識網絡：

（1）一組鄰邊相等的平行四邊形是菱形；

（2）四條邊都相等的四邊形是菱形；

（3）對角線互相垂直的平行四邊形是菱形；

（4）對角線互相垂直且相等的四邊形是菱形.

提示2：這些方法能用來解決本問題的有哪些？怎樣尋找思路？

提示3：是否在幾種思路中優先考慮最優思路？

學生們通過分析對比，發現本題特殊之處在于：已知一組對邊平行，一組對角相等，所以優先考慮“一組鄰邊相等的平行四邊形是菱形”來證明，其他方法的證明都不可取.

方法1：因為AD∥BC，所以∠BAD+∠B=180°. 因為∠BAD=∠BCD，所以∠BCD+∠B=180°，所以AB∥DC，所以四邊形ABCD是平行四邊形. 所以∠B=∠D. 因為AM=AN，AM⊥BC，AN⊥DC，所以Rt△ABM≌Rt△ADN. 所以AB=AD，所以平行四邊形ABCD是菱形.

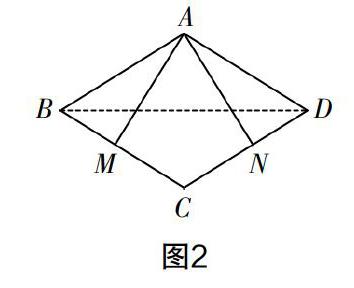
方法2：如圖2，連接BD，因為AD∥BC，所以∠ADB=∠DBC. 因為∠BAD=∠BCD， BD=BD，所以△ABD≌△CDB，所以AD=BC. 所以四邊形ABCD是平行四邊形，所以∠ABC=∠ADC. 因為AM=AN，AM⊥BC，AN⊥DC，所以Rt△ABM≌Rt△ADN，所以AB=AD. 所以平行四邊形ABCD是菱形.

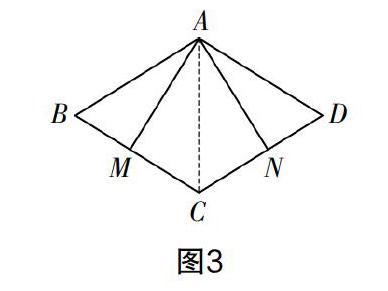
方法3：如圖3，連接AC，因為AM=AN，AC=AC，AM⊥BC，AN⊥DC，所以Rt△ACM≌Rt△ACN，所以∠ACB=∠ACD. 因為AD∥BC，所以∠ACB=∠CAD，所以∠ACD=∠CAD，所以DC=AD. 因為∠BAD=∠BCD，所以∠BAC=∠ACD，所以AB∥DC，所以四邊形ABCD是平行四邊形，所以平行四邊形ABCD是菱形.

通過以上的提示，學生的數學元認知知識對問題解決有目標導向作用，在頭腦中建立一個解決該問題的知識網絡，從中尋找解決問題的最佳方法，最后形成穩定、有效、可控制的元認知技能，從而促進學生解決問題能力的提高和思維方式的遷移.

3. 實施計劃

當學生找到解題思路后，教師繼續提示：

（1）你充分地進行雙向推理了嗎？

（2）你選擇的方法需要添加必要的輔助線嗎？

通過提示，讓學生理清了雙向推理的證明思路. 例如第一種方法（不需添加輔助線）的分析過程：

①要證四邊形ABCD是菱形四邊形ABCD是平行四邊形（要證），AB=AD（要證）；

②要證四邊形ABCD是平行四邊形？圯AD∥BC（已知），AB∥DC（要證）；

③要證AB∥DC？圯AD平行BC（已知）？圯∠BAD+∠B=180° ∠BAD=∠BAC？圯∠BAC+∠B=180°（證平行）；

④要證AB=AD？圯△ABM≌△ADN？圯AM⊥BC，AN⊥DC，∠B=∠C，AM=AN.

幾何證明題關鍵在于分析推理，在分析的過程中教師要通過一些提示語，教會學生如何從問題找條件來分析推理，或從條件推結論分析推理，使學生能展示思考分析過程. 這樣學生的思維才能得到有效訓練，慢慢積累元認知經驗，形成元認知習慣，提高元認知能力.

4. 回顧解題

解完題目之后，教師引導學生思考：（1）本題的思路特點是什么？（2）這個思路還可以用來解決什么問題？學生據此展開討論.

解題后，引導學生再現解題的經歷，抽取解決問題的關鍵，總結解題過程的經驗與教訓，反思解題過程的成敗得失及其原因，從思維策略的高度對解題過程進行總結，從中概括出一般性規律，概括出點點滴滴的新經驗、新見解、新體會，以及對問題進行推廣、深化，可以有效培養學生評價、調節、監控、完善等元認知能力.

結束語

在解題教學中，數學元認知的監控、調節作用能幫助學生正確解題，所以必須注重培養學生養成良好的認知方法和思維策略.

1. 對于復雜的題目，應當幫助學生建立一個有層次的目標體系，即把問題的解決分成幾個有序的階段，建立階段目標，一步一步地逼近整個問題的解決. 這樣可以在整個解題過程中都能清楚地認識自己目前所處的位置，養成優質的元認知經驗.

2. 在解題中注重對學生解題思維的訓練，利用一些在數學解題過程中常用的思維方法，指導學生根據問題的特點和要求靈活和綜合運用數形轉換、分類討論、歸納猜想、類比聯想等常用的數學解題策略去分析問題和解決問題. 還應著重強調這些策略使用的條件，使策略成為“條件化的知識”，最后形成穩定而有效的、可控的元認知技能.

3. 不斷引領學生對學習過程及其結果、學習策略及其效果進行監控、評價，充分發揮元認知本身所具有的監控、調節特點，加強元認知體驗訓練，使學生的元認知能力得到充分的發展.

總之，解題教學的目的不是純粹為了教會學生解幾道題或幾類題，而是要讓學生“既看到樹木，又見到森林”. 要在解題的實踐中讓學生獲得題感，再從題感中提煉和升華數學思想方法，最終內化成為學生的一種元認知能力.