倒掛井壁法豎井襯砌結構受力分析

張增峰

（上海市城市建設設計研究總院（集團）有限公司,上海市 200125）

0 引言

地鐵暗挖車站一般埋置較深，且地面建筑物多，交通繁忙，施工時為運輸隧道內材料并增加土石的出入口需設置施工臨時豎井。

豎井結構設計計算時通常是將其簡化為平面問題處理，采用半經驗的方法。但是豎井結構為保證足夠剛度，往往在內部設置圈梁、腰梁等加強結構，同時豎井壁承受的側向荷載隨深度的增加也在不斷變化，這與平面問題的假設條件不符。因此在設計中應考慮豎井結構的空間效應。

井壁側土壓力的分布主要可歸納為兩種：（1）線性增加型——不考慮井筒掘進半徑的影響，隨深度呈曲線增加。（2）極限型——地壓力與井筒半徑有關，深度達到一定值時，地壓力趨于一極限值。徐偉等[1]通過三維離型機模型試驗，得到深厚覆蓋層下豎井井壁外側的應變數據，其變化趨勢為豎井井壁環向應變整體上先增后減，在距地表0.5H（H為豎井深度）處，豎井應變達到最大值。崔廣心[2]通過研究指出，深層地壓的復雜性大于目前的認知，對于達到某一深度后水平地壓趨于定值的結論并未得到足夠的工程實測資料證實，人為減小地壓值很可能給工程造成隱患。胡金平等[3]通過有限元模擬認為，由于井筒周圍圍巖開挖卸載，應力迅速減少，可能因井底成為臨空面而導致井筒側壁出現拉力。朱正國等[4]研究認為：豎井圍護結構是一種四邊相互支撐的閉合結構，具有顯著的空間受力特性，經典土壓力理論與假設工程實際相差較大，導致圍護結構設計偏于保守。

圍巖壓力計算是豎井結構設計的基礎，若側壓力值取值太大將使結構設計過于保守，造成不必要的浪費，若取值太小則結構設計偏于不安全。目前設計院一般采用半經驗方法，將其簡化為平面應變模型，取最大側壓力處的襯砌內力進行包絡設計。該方法雖未發生較大的問題，但井壁在不同深度、不同土層采用相同的格柵間距不符合客觀實際且設計概念不清晰。

本文以貴陽市軌道交通3號線北京路站1號豎井結構設計為背景，建立三維有限元數值模型，分析不同側向土壓力模型下結構的受力情況并與傳統平面應變模型計算結果比較，得出相應結論，為以后類似工程提供優化設計借鑒。

1 工程背景

貴陽市軌道交通3號線北京路站位于安云路與北京路十字交叉路口下方，與軌道交通1號線換乘，1號線車站沿安云路呈南北方向布置，3號線車站沿北京路呈東西方向布置。從經濟角度考慮，1號豎井與車站風井結合設置，位于車站西南角（見圖 1）。

1.1 車站豎井地質情況

圖1 1號豎井總平面圖

本站豎井開挖深度范圍內主要涉及＜1-3＞塊石層、＜4-1-1＞硬塑紅黏土、＜4-1-2＞可塑紅黏土、＜14-2-3＞中風化白云巖。紅黏土呈黃褐色、棕黃色，軟塑狀，土質純，具有高液限、遇水軟化、失水強烈收縮、裂隙發育、易剝落的工程性質，局部具弱膨脹性；中風化白云巖呈灰色、淺灰色厚層至塊狀細-中晶白云巖或紫紅、肉紅、灰黃薄至中厚層泥晶灰白云巖夾膏鹽巖，時夾溶塌角礫巖，巖芯敲擊聲較脆，節理較發育。車站豎井地層參數見表1。表1中：hi為各土層厚度，m；γ為土體天然重度，kN/m3；ν為泊松比；Eref為地層彈性模量，MPa；cref為土體粘聚力，kN/m2；φy為土體內摩擦角，（°）。

表1 地層參數表

1.2 支護結構參數

豎井采用倒掛井壁法施工，井壁初期支護采用C25噴射混凝土，厚度350 mm，格柵鋼架采用4根25主筋，每榀格柵鋼架中心間距0.5 m，側壁采用22砂漿錨桿，長3.5 m，梅花形布置，水平間距1.0 m，水平夾角30°。井口設置1.0 m×1.5 m鎖口圈梁，開橫通道馬頭門上方設置0.6 m×0.8 m腰梁。豎井設計深度為32.1 m，豎井底部采用8@200 mm×200 mm鋼筋網（雙層）封底。1號豎井平、剖面如圖2所示。

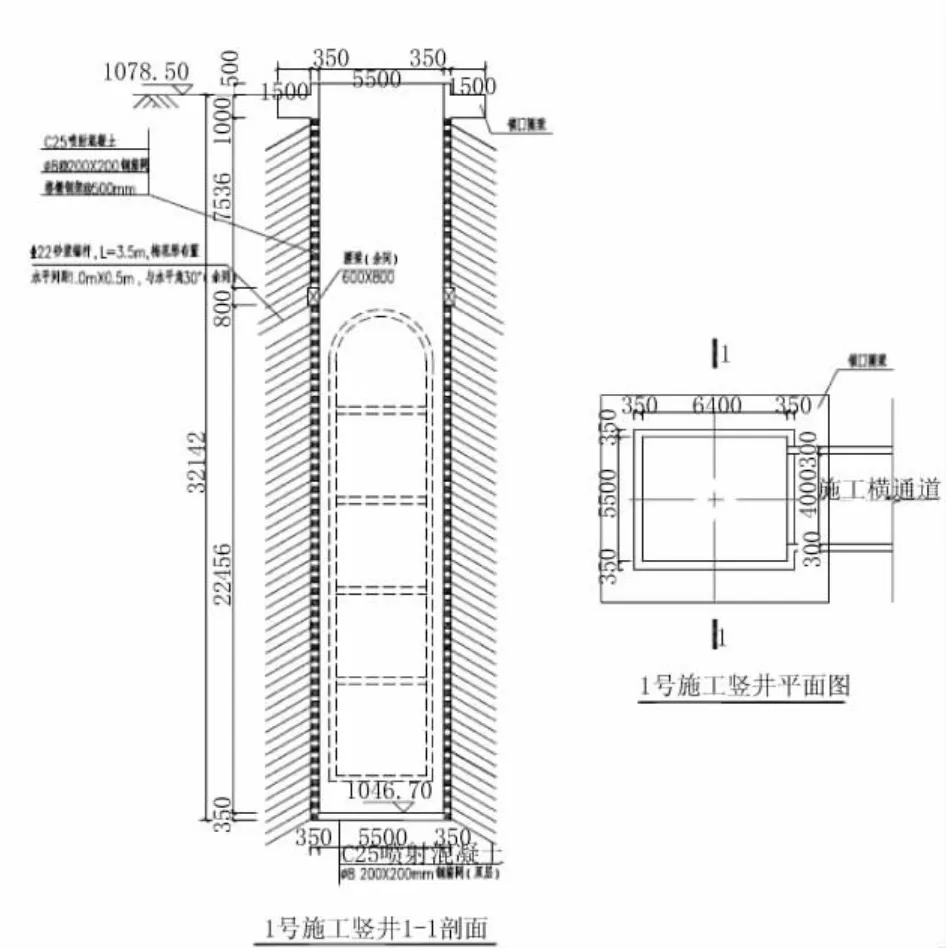
圖2 豎井支護結構平、剖面圖（單位：mm）

2 豎井側向壓力

2.1 側向壓力模型的選擇

（1）朗肯土壓力公式因概念清晰、計算簡單而被廣泛應用于土壓力計算中。根據朗肯土壓力計算公式可得：

式中：Pka為主動土壓力系數；γi、hi分別為第 i層地層重度（kN/m3）和厚度（m）；φi為第 2 層土體內摩擦角，（°）；ci為第 2 層土體的黏聚力，kPa。

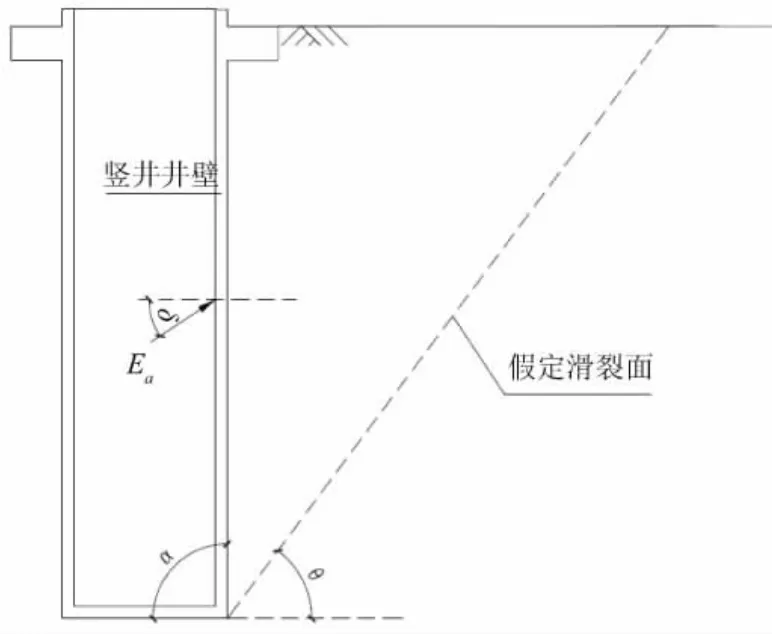
圖3 豎井井壁土壓力計算

（2）側向巖土壓力也可采用庫倫土壓力公式求解。根據平面滑裂面假定（見圖3），主動土壓力合力可按照下列公式計算：式中：Ea為相應于荷載標準組合的主動土壓力合力，kN/m；H為豎井深度，m；δ為土對擋土墻墻背的內摩擦角，α為支擋結構墻背與水平面的夾角；其余符號含義同公式（1）。

擋墻側壓力分布可根據錨桿層數、擋墻位移大小、支護結構剛度和施工方法等因素，簡化為三角形、梯形或當地經驗圖形。北京路站豎井主要位于中風化灰巖中，側壓力可近似按照圖4確定。

圖4 豎井井壁側壓力分布圖

圖中 豎井井壁的側壓力:

式中：eah為相應于作用的標準組合時側向巖土壓力水平分力，kN/m2。

（3）《公路隧道設計細則》（JTL/T D70—2010）中指出，對于公路隧道通風豎井圍巖壓力可按秦氏方法進行計算，假定豎井周圍每層巖石受到破壞時出現滑動棱柱體，將其上的覆蓋層視為作用于破壞棱柱體上的均布荷載，則豎井的圍巖壓力為：

2.2 側向壓力計算

（1）根據朗肯土壓力計算公式（1），豎井側向壓力隨深度的變化值見表2。表2中，當計算值Pka＜0 時，取 Pka=0。

表2 圍巖側向壓力變化表（朗肯土壓力）

（2）采用庫倫土壓力公式（2），豎井側壁承受的主動土壓力Ea計算如下：

取 c=90 kPa，γ=27 kN/m3，H=32.1 m，φ=27°，因墻背粗糙，可取δ=0.5φ=13.5°，將以上參數代入公式（2）可得：

由公式（3）可得：

（3）采用秦氏算法進行計算，豎井側向壓力隨深度的變化值見表3，根據《公路隧道設計細則》中表20.2.7-1，其中的λn取相應土層的平均值。

表3 圍巖側向壓力變化表（秦氏算法）

3 有限元計算

3.1 模型建立

3.1.1 平面應變模型

平面應變模型基于結構分析軟件ANSYS，采用荷載-結構模型平面桿系有限元法進行豎井襯砌結構的計算與分析。襯砌結構選取梁單元（beam3），圍巖彈性抗力采用彈性桿（link10），豎井的側向彈簧剛度取所在土層水平基床系數。荷載結構計算簡圖見圖5。

3.1.2 三維梁-殼單元模型

三維梁-殼單元模型同樣基于結構分析軟件ANSYS，采用荷載-結構模型三維梁-殼有限元法進行豎井襯砌結構的計算與分析。襯砌結構選取殼單元（shell63），鎖口圈梁采用梁單元（beam188）。荷載結構計算模型見圖6。

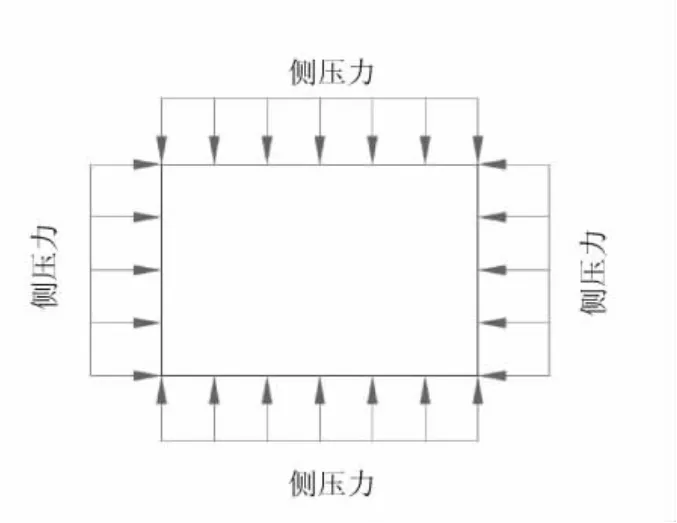
圖5 豎井襯砌計算簡圖

圖6 豎井襯砌三維梁-殼單元模型

3.2 計算結果及安全分析

取各側向土壓力計算模型計算所得的側向壓力最大值加載于平面應變模型中，分別得出結構的彎矩、軸力及最不利截面出現的位置。

將各測向土壓力計算模型計算所得的側向壓力隨深度變化值加載于三維梁-殼單元模型中，得出豎井井壁的彎矩、軸力以及最不利截面出現的位置。

平面應變模型計算結果見圖7～9，平面應變模型最不利截面處內力及配筋量見表4。

圖7 朗肯土壓力計算襯砌內力

三維梁-殼單元模型計算結果見圖10～12，三維梁-殼最不利截面處內力及配筋量見表5。

圖8 庫倫土壓力計算襯砌內力

圖9 秦氏土壓力計算襯砌內力

表4 平面應變模型最不利截面處內力及配筋量

圖10 朗肯土壓力計算井壁內力（單位：kN·m）

圖11 庫倫土壓力計算井壁內力（單位：kN·m）

對平面應變模型與三維梁-殼單元模型計算結果進行對比可知，平面應變模型所得的彎矩及軸力均大于三維梁-殼單元模型的計算結果，且無法了解最不利斷面所處深度；后者考慮到豎井結構的空間效應，更符合豎井襯砌的實際受力工況。

圖12 秦氏土壓力計算井壁內力（單位：kN·m）

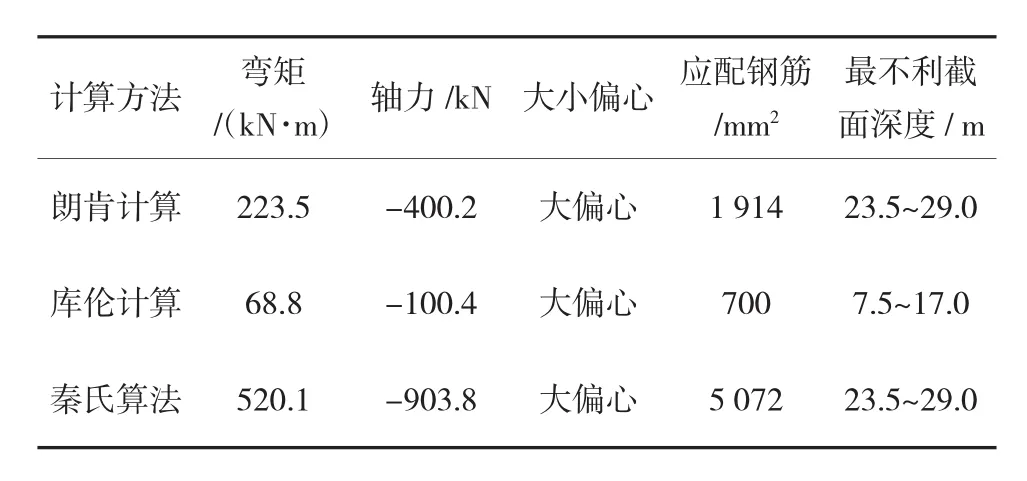
表5 三維梁-殼單元模型最不利截面處內力及配筋量

三維梁-殼單元模型計算所得井口至馬頭門上方（深度約6～7 m）豎井井壁的內力較小。豎井襯砌最不利斷面往往處于井底以上5～8 m范圍內。

根據計算結果，采用朗肯土壓力公式、秦氏算法計算所得井壁的彎矩及軸力均遠遠大于庫倫土壓力計算結果。若采用秦氏算法計算所得的結果進行襯砌配筋，則初支結構襯砌配筋量過大。

對本地區相似車站及區間豎井支護后的工程進行類比，實際襯砌每延米配筋為425（實配受拉鋼筋面積As=1 964 mm2/m），配筋量均遠小于以上秦氏算法計算所得的理論值。每榀格柵鋼架配筋見圖13。

根據類似工程的監測數據，采用朗肯土壓力計算結果進行設計的襯砌結構，在使用期間井壁的水平變形已收斂，井壁周邊無明顯裂縫，基本處于穩定狀態。

圖13 格柵鋼架配筋詳圖（單位：mm）

4 結論

（1）采用秦氏算法計算的圍巖側向壓力在同一巖層中線性增加，井底處圍巖壓力較大。根據開挖應力分析表明，因井壁周圍圍巖開挖卸載而使應力迅速減小，用秦氏算法計算所得豎井側向壓力過于保守，造成設計過程中配筋困難。

（2）朗肯主動土壓力的計算假定為：墻背直立光滑、土體表面水平，而豎井襯砌結構為噴射混凝土，且每榀格柵周邊均勻打設砂漿錨桿，墻背粗糙且與周邊地層結合較好，故若圍巖側向壓力直接采用朗肯土壓力計算可能與實際工況存在偏差，但按此方法計算可基本滿足安全施工的要求。

（3）庫倫土壓力假設破裂面不確定，若豎井開挖深度內巖（土）層分布復雜，則破裂面無法確定，從而導致墻背主動土壓力計算結果偏差較大，在復雜地層中難以把握井壁的實際承受側向壓力，按庫倫土壓力設計襯砌結構可能給工程造成隱患。

（4）豎井設計忽略了鎖口圈梁、腰梁、封底格柵的剛度，未考慮其對豎井的約束作用，且豎井在馬頭門上方的襯砌內力較小，宜適當增大格柵間距。

（5）豎井的圍巖應力場研究不夠透徹，導致豎井襯砌結構設計過于保守。建議豎井圍巖設計時根據更多工程經驗，修訂或改進傳統朗肯土壓力理論，便于設計人員在工程中應用。