時間序列數據挖掘中的特征表示與相似性度量方法研究分析

王培屹

（鄭州幼兒師范高等專科學校，河南 鄭州 450000）

1 引言

時間序列數據能夠隨著時間而變化，它的產生過程極易受環境的影響，而且會伴隨一定的噪聲。由于數據極為繁雜，研究的難度很大，然而其中蘊含著有非常價值的信息，這類信息對于社會實踐具有重要的意義。時間序列數據相較于普通數據而言，它是高維的，在實踐過程中，針對時間序列數據，通常都必須對其進行降維，具體方法有兩種：其一是進行全局特征分解；其二是局部特征提取。時間序列相似性度量的作用是挖掘時間序列數據中存在的有價值的信息，使其更好地應用于社會生產實踐。

2 特征表示方法

時間序列特征表示的含義：針對原時間序列數據，使之轉變成另外一個不同論域中的數據，并實現其降維，在進行降維之后，對于低維空間的數據，也能最大限度地反映出原時間序列的信息。就目前而言，已經出現很多特征表示方法，下面就簡單介紹幾種：

2.1 分段線性表示方法

分段線性表示方法與其他表示方法相比，更加直觀和簡單，它在時間序列數據挖掘中的應用最為普遍，通常和時間序列相似性度量方法相互配合來使用。利用這種方法來分割時間序列，需要建立線性模型。根據分割方法的不同，采用的分割策略也不同。據分析研究可知，對于滑動窗口方法和自底向上的方法而言，其時間復雜度和序列長度的關系是前者為后者的平方階；而對于自頂向下的方法而言，其時間復雜度為線性階。滑動窗口的方法，在某些情形下，對時間序列的擬合程度不夠好，對于原時間序列中蘊含的變化信息，不能夠全面地反映出來。對于自頂向下方法而言，其時間復雜度雖然相對來說更高一些，然而，在圖像處理以及機器學習方面，它的應用極為廣泛。通過對時間序列進行識別和掃描，尋找其中的關鍵性片段，如：波谷和波峰，然后再自頂向下切割。遺憾的是，對于噪聲數據，它一樣比較敏感。通過對比可知，自底向上方法具有其他方法不具備的兩大優點：第一，這種方法的時間復雜度對數據集擁有線性擴展性；第二，在分割大部分時間序列數據集時，它的效果更好。通過對比以上三種分割方法，各有優點和不足，經過研究提出了一種更好的分割方法，這種方法集中了自底向上以及滑動窗口各自的優勢，不僅使在線分割得以實現，而且，對時間序列數據的擬合效果也非常好。

2.2 分段聚合近似表示方法

分段聚合近似表示方法(PAA)主要是通過平均分割時間序列并根據各段序列的平均值來表示原時間序列。這種方法以m長度的時間序列為對象，將其切割為w段，每段長度為k，對于該長度為m序列段，用k來表示，壓縮比為降維數為w，從而實現降維。若要確定特征序列，離不開k和w，如果k值越大，或者w值越小，那么近似表示該時間序列的效果就越不好，同時也會丟失更多的信息，至于其降維幅度，則會越大；如果k值越小，或者w值越大，則會與上述情況完全相反。所以，實現了近似表示效果的最大化，就不能獲得更大的降維幅度，需要權衡利弊，找到兩者之間的平衡。在時間序列中，有極大值、極小值等重要信息，而這種方法運用了平均值，從而造成這些重要信息丟失，而且，對于那些均值相同，但形態趨勢存在極大差異的序列，這種方法的使用會將它們表示成相同的均值信息特征。因此，相關專家學者對這種方法進行了改進，在表示時間序列的過程中，使用均值的同時，兼顧了分段序列的斜率。結合時間序列自身的特點，將其分為不等長的段，仍然通過均值來反映時間序列的特征，即自適應分段常量近似方法，為找到這種方法的分割點，通過采用動態規劃的方法來實現對時間序列的最優化分割，在某些情形下，可以采用貪婪算法進行次優分割，從而使算法的效率大大提高。

2.3 符號化表示方法

符號化表示方法的含義：實現時間序列向字符串序列轉換的過程。當挖掘時間序列數據中的信息時，傳統挖掘方法局限于定量數據，在分析和解決問題方面存在很大的不足。在數據結構中，字符串具有兩大優點：第一，具備特定的數據存儲結構；第二，其操作算法速度快。近幾年，有很多和字符串有關的算法的應用越來越廣泛。對于一些特殊的實際問題，很難用具體的定量數據來反映，而通過字符型數據卻能收到令人意外的效果。在符號化表示方法之中，符號化聚合近似表示方法(SAX)屬于最具代表性的一種，它是在PAA的基礎上，加以改進形成的一種表示方法。這種表示方法先將時間序列平均分為若干段，并實現原時間序列的Z標準化，然后再針對數據空間，將其分為概率相同的幾個部分，并以不同字符進行表示，最后獲得的均值序列便是用各部分的字符表示的。因為SAX是基于PAA的一種符號化表示方法，所以也擁有著PAA的某些缺陷，因此，相關學者提出了兼顧均值和方差并其轉化為符號，實現在二維空間下的符號化表示。

3 相似性度量研究

相似性度量方法的主要作用是：權衡不同對象之間的關系。在挖掘時間序列的過程中，相似性度量發揮著至關重要的作用。

3.1 歐氏距離

假設有時間序列 Q={q1，q2，……qm}和 C={c1，c2，……cm}，如果采用M inkowski距離度量方法，則

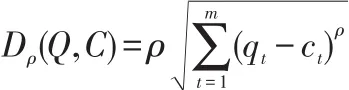
在距離度量方法中，上式是通用的，p值的變化會帶來距離度量方式的變化。當p=1時，它表示曼哈頓距離；當ρ=∞時，它轉變為 L∞范數，且滿足；當p=2時，它表示歐氏距離，它是應用最普遍的一種距離度量方法。通常情況下，若兩條時間序列長度相同，歐氏距離可以直接進行距離度量，然而，在大多情形下，它必須同特征表示方法相結合。比如，針對分段之后的時間序列，利用歐氏距離的方法，對擬合序列段直線斜率的相似性進行精密的計算，將時間序列符號化之后，同樣利用歐氏距離的方法，在降維空間中，進行相似性度量，在譜分解中進行能量計算，從而使特征序列的相似性度量得以實現。但是，因為歐氏距離對時間序列噪聲以及序列段突變有很強的敏感性，對于數據的預處理操作依賴性較強，而且，對于時間序列的位移不能進行有效的識別。最重要的是，它只局限于度量相同長度的時間序列段，針對不同長度時間序列，就不適用。所以，歐氏距離一般情況下，都要充分結合時間序列的特征表示方法來度量時間序列相似性。尤其是在針對特征表示之后的空間進行度量時，一定要滿足其下界的要求，避免有所漏報。

3.2 動態時間彎曲

動態時間彎曲的具體含義是：借助彎曲時間軸，來實現對時間序列的匹配映射。它最初的作用是對語音數據進行處理，后來又被用作時間序列相似性的度量。動態時間彎曲在兩條時間序列Q={q1，q2，……qm}和C={c1，c2，……cn}之間，尋找出最好的彎曲路徑，從而得到DTW(Q，C)，它是最小的距離度量值。只需要符合邊界條件的要求，P=(p1，p2……pk)可以用來表示連續性路徑，其中，qik與cjk之間的對應關系可以pk表，qik和cjk的彎代價以d(pk)來表示，一般情況下取2，……n，在這一系列彎曲路徑中，有一條最優路徑可以使彎曲總代價最小，即

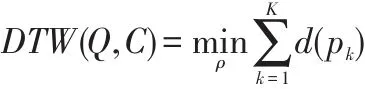
我們可以采用動態規劃來構造一個代價矩陣R來求解,即：

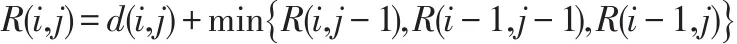
其中，i=1,2,…m ，j=1,2,…n，R(0,0)=0，R(i,0)=R(0,j)=+∞，R(m,n)即動態彎曲時間序列Q和C的最小距離值，即 DTW(Q,C)=R(m,n)。

通過對比動態時間彎曲與歐氏距離，不難發現：（1）前者能夠度量的時間序列可以有兩種類型，即：長度相同的、長度不同的；后者能夠度量的時間序列只有一種，即：長度相同的。（2）針對時間序列的突變點，前者不敏感，而且，也更加適合對其進行度量；后者則不然，針對這類異常時間序列，敏感度較高，不適合對其進行度量。（3）前者能夠進行異步相似性比較，后者只局限于同步比較；（4）針對時間復雜度，前者為O(m2)，后者為O(m)；（5）前者不滿足三角不等式，后者則滿足。

3.3 符號化距離

針對時間序列的特征表示，符號化距離能夠將之轉變為字符串，轉變成字符串之后，其度量方法也隨之發生了改變，即由定量數據轉變為定性符號。它是在歐氏距離的基礎上形成的度量方法，它針對時間序列，做了標準化處理，使之能夠滿足正態分布，然后再將之轉變為字符串。通過查詢正態分布圖，可以知曉字符間距離。據相關資料顯示，這種距離方法也符合下限要求，通過它來搜索時間序列相似性時，可以避免漏報情況的出現。編輯距離的含義是：實現兩個字符串之間的轉換所須的最少步驟，如刪除字符、插入字符等。第一步：將時間序列轉變為字符串；第二步：針對兩個字符串，借助于編輯距離，度量二者的相似性。編輯距離的主要優點：能夠使挖掘算法的性能得到全面提高，更重要的是，對于其具體操作過程，更容易理解和掌握。然而，也存在一些缺點，比如：當兩個時間序列不同步時，其相似性度量不能發揮出更好的效果。

4 未來研究方向

隨著科學發展的日新月異，我國在時間序列方面的研究也取得了驕人的成績，被應用于社會生活的各個層面，為社會的發展和經濟的建設做出了重大的貢獻。比如：在醫療領域中，針對病人群體，可以用來檢測其中的異常個體；在金融領域中，可以用來監視消費支出，避免欺詐現象的產生等。但是，在研究的過程中，也逐漸暴露出了一系列的問題，應該給予充分的重視。

分段線性近似表示方法的應用非常普遍，屬于最常用的方法之一，它針對時間序列的關鍵點和關鍵形態，進行分析和識別，借助于直線段，實現原時間序列的模擬。這種方法的優點是：針對時間序列的特征表示更為直觀易懂；它的缺點是：擬合線段數目難以確定。所以，如何有效地對時間序列進行分段線性近似表示是一個非常有意義的研究課題，也將是未來一個重要的研究方向。

動態時間彎曲相對來說伸縮性更好，它可以略過時間序列的特征表示，進行相似性比較。相比于歐氏距離，動態時間彎曲具有兩大優勢：第一，對異常點沒有敏感性；第二，可以度量不等長的時間序列。但是，因為動態時間序列搜索最優彎曲路徑的時間復雜度比較高，所以，對于數量多的時間序列，它不適合進行相似性比較，應用范圍具有很大的局限性。而且，動態時間彎曲還有一個缺點就是：太過于依賴時間序列數據值，對于局部數據的特征則沒有考慮，無法對那些數據相近但形態不同的時間序列進行相似性比較。因此，如何有效提高動態時間彎曲方法的效率和精度是將來的一個重大課題。目前，關于這方面的研究，基本上都偏重于靜態時間序列數據，至于動態時間序列數據，研究文獻則相對來說比較少。因為動態時間序列數據隨時間變化而變化，這就要求特征表示方法和相似性度量方法必須具備高效、穩定的特點。

5 結束語

時間序列是一種應用極為廣泛的數據，通過數據挖掘技術能夠從中獲取有價值的信息，這類信息有助于國家的經濟建設，具有非常重要的現實意義。在數據挖掘的過程中，必須做好兩項基礎性的工作，分別是：特征表示、相似性度量。這兩項工作能夠為數據挖掘任務提供有效的數據處理方法和技術支持。本文客觀地闡述了相關方法的優點和缺點，希望能夠為時間序列數據挖掘領域的研究提供幫助。