高中數學函數問題的探究
尹學明
(浙江省臺州市第一中學 318000)
一、函數與方程
函數和方程具有密切的聯系,方程的解其實是函數圖象與x軸的交點.函數y=f(x)可以當做方程f(x)-y=0進行分析和探究,在函數的變化中,有時候需要通過方程來求出滿足條件的一些關鍵量,這就是方程思想.函數與方程是貫穿于學生整個高中階段的,引導學生進行數學量與量之間關系的分析和探究,并將這些變化反映到解析式、圖象以及列表中,從而讓學生更容易地進行問題的理解和解決.高中方程可以用f(x)=0或f(x)=g(x)的形式表示,f(x)=0的根就是函數y=f(x)圖象與x軸的交點,f(x)=g(x)的根就是函數y=f(x)與y=g(x)圖象交點的橫坐標.
例1 (2016年浙江高考12題)設函數f(x)=x3+3x2+1.已知a≠0,且f(x)-f(a)=(x-b)(x-a)2,x∈R,則實數a=____,b=____.
解析本題主要體現了函數和方程的思想,在掌握函數解析式的情況下,將x與a分別代入函數中,得出f(x)-f(a)=x3+3x2-a3-3a2,然后再為(x-b)(x-a)2化簡即可構造出有關a、b的方程組,從而求解.
二、函數與不等式
函數思想在不等式的分析和解答中也具有重要的意義,可以通過不等式的信息進行函數的構造,然后用函數的性質和圖象進行分析,往往能起到事半功倍的效果.高中的不等式基本上可以用f(x)>0、f(x)<0或是f(x)>g(x)進行表示,當然也可以在圖象上通過上下位置的關系進行闡述.
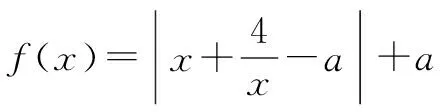
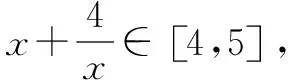
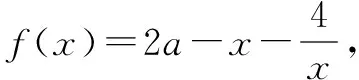
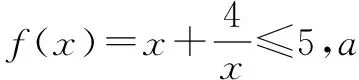
當4
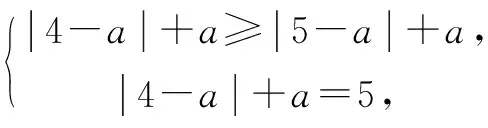
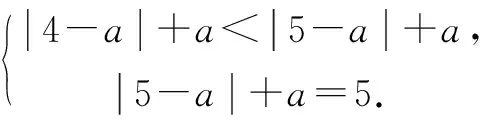
三、函數與導數
導函數是高考的重要內容,尤其是一些簡答試題中,常常有導函數的問題,這就要求學生要運用函數思想進行導函數單調性、極值的問題分析和解決,同時能夠將函數的各種形式進行轉化,從而對有關導函數的問題能夠從容應對.
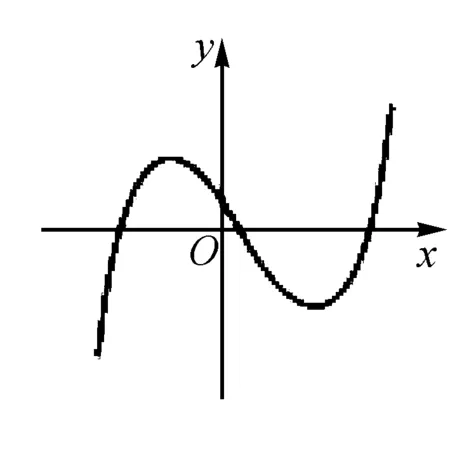
例3 (2017浙江高考7題)函數y=f(x)的導函數y=f′(x)的圖象如圖所示,則函數y=f(x)的圖象可能是( ).
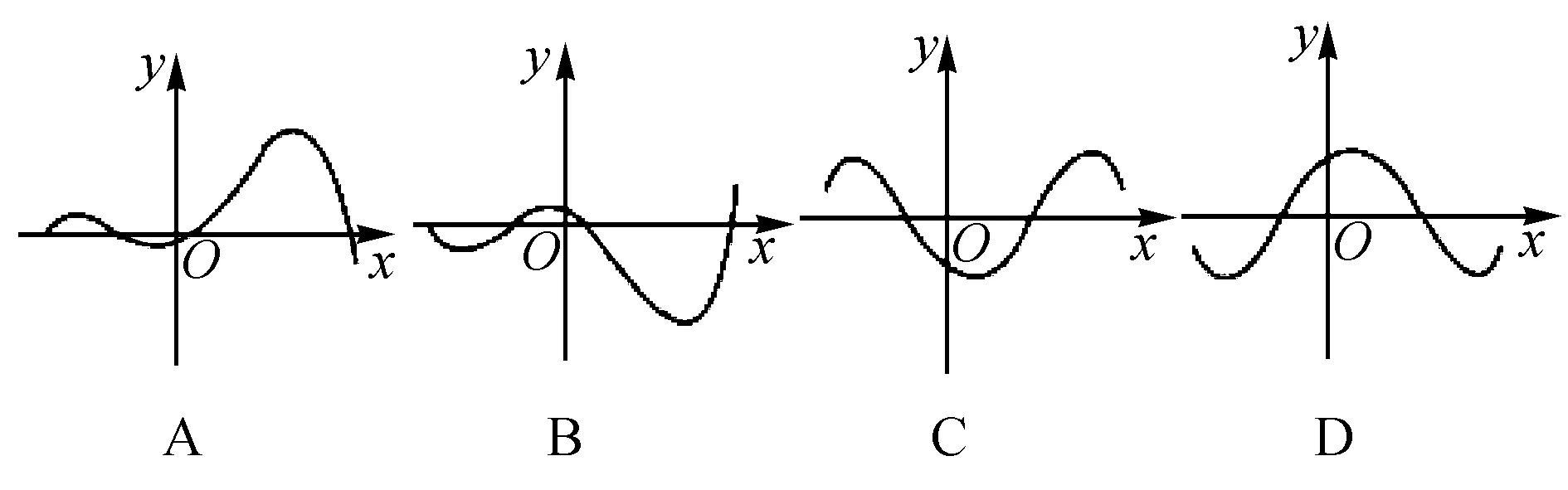
解析本題主要要求學生能夠從導函數的圖象進行函數圖象的判定,由導函數的性質可知,f′(x)<0,函數單調遞減,f′(x)>0函數單調遞增,由導函數的圖象可知,原函數先遞減再遞增,然后在遞減再遞增,由此可以得出答案.
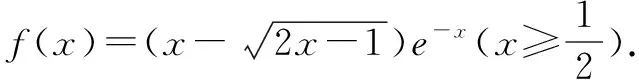
(1)求f(x)的導函數;
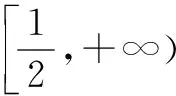
解析本題第一問直接通過函數求導得出結果即可,第二問需要運用第一問中的導函數,進行原函數極值和單調性的計算,同時滿足f(x)≥0的條件,則可以確定f(x)的取值范圍.
總之,從近幾年浙江高考的趨勢來看,函數思想在高考中占有絕對的比例,就拿2017年高考來說,浙江試題中一共有5題,知識點涉及二次函數、方程、不等式、導函數、三角函數、函數模型等,這就要求教師在教學的時候,要結合教學內容,將函數思想貫穿在數學教學的始終,培養學生運用函數進行具體問題的分析和解決,從而提升學生數學能力,促進學生數學素養的全面發展.

