基于矩陣譯碼算法的改進研究

范 迪 蕭 楓 唐 聃

(成都信息工程大學軟件工程學院 四川 成都 610225)

0 引 言

隨著計算機技術的迅猛發展，信息技術在各個行業和領域都得到廣泛的普及，數據也呈爆炸性的增長，使得人們對存儲系統的要求越來越高。日益增長的存儲需求使得存儲系統中的存儲節點數量和單節點容量都呈指數級增長，這就意味著發生節點失效的概率以及單節點中的扇區失效的概率越來越大，因此數據容錯是存儲系統中一項不可或缺的關鍵技術。目前使用較多的容錯技術為多副本復制技術，通過復制副本進行容錯。另外一種是糾刪碼容錯技術，通過編碼進行容錯。編碼理論始于1948年Claudo Shannon發表的著名文獻[1]。最初編碼理論的主要應用領域為通信，糾刪碼是為了解決網絡傳輸問題中多址傳送而提出來的，比較重要的一篇文獻是 1997 年Luigi Rizzo的文獻[2],該文主要提出了利用糾刪碼提高通信協議可靠性的方法，使用前向糾錯碼 Reed Solomon 來解決網絡傳輸中一定數量的數據包丟失，原始數據還能恢復，并提出了一套可行的方案，同時該文提出糾刪碼可以應用于分布式存儲系統。糾刪碼技術主要是依靠糾刪碼算法將原始的數據進行編碼得到冗余元素后存儲，以達到容錯的目的。在存儲系統中，它的主要思想是通過將k塊原始的數據元素編碼得到m塊冗余元素，當其中有m塊元素失效時，可以通過一定的解碼算法利用余下的元素將丟失元素恢復出來。與多副本容錯技術相比，糾刪碼容錯技術可以在顯著降低存儲空間消耗的同時提供相同甚至較高的數據容錯能力。

對于糾刪碼而言，最重要的就是其編解碼算法，每一類糾刪碼都有本身所對應的解碼算法，優秀的解碼算法可以幫助提高存儲系統故障恢復的效率。同時也存在一些通用性的解碼算法。例如歸并譯碼和矩陣譯碼等。文獻[3]中提出的一種在二元域上的糾刪碼解碼算法(簡稱歸并譯碼)，通過對校驗矩陣分塊并求逆來重建磁盤數據元素，但是此算法的運算過程涉及到逆矩陣的計算，因而當恢復單錯時效率較高，一旦出現多錯，求逆運算會很大程度影響到運算的速度，從而影響解碼效率。文獻[4]中提出一種針對糾刪碼的通用解碼算法，這種算法基于生成矩陣及其偽逆矩陣(簡稱矩陣譯碼)，對于丟失數據扇區，一般聲明為兩種結果，一種是算法可恢復即理論上可恢復，此時算法會提供一個由可讀數據構成的公式來恢復丟失扇區，一種是理論上即不可恢復的扇區。對于陣列碼，矩陣譯碼算法還可以恢復隨機數據扇區的故障，解決了隨機扇區丟失的問題，由此提供了更好的實用性，也提高了存儲系統的性能。矩陣譯碼算法既解決了陣列碼中隨機扇區丟失的恢復問題，同時摒棄了求逆矩陣的運算，使其效率很高；同樣是一種通用性的解碼算法，適用于任意的糾刪碼，最適合用于陣列碼。矩陣譯碼算法存在優點，同時也有不足，其不足之處在于當故障類型包含冗余節點錯誤時，不能隨原始數據節點同時恢復，需要在數據節點恢復完成后利用編碼將其恢復，由此會降低故障恢復的效率。本文將對矩陣譯碼算法的優勢進行描述，然后對其不足進行改進研究，最后基于改進研究算法做出具體的實驗分析。

1 矩陣譯碼算法

矩陣譯碼算法是一種通用的經典糾刪碼解碼算法。其最大的特點在于：(1) 通用于任意糾刪碼；(2) 可以恢復隨機數據節點扇區的丟失。因為陣列碼特殊的矩陣結構，矩陣譯碼算法可以更好地應用在陣列碼中。對于普通的糾刪碼解碼，矩陣譯碼同時也消除了矩陣求逆的運算過程，另外其效率也較高。

1.1 基本概念及定義

為了更好地描述算法，更加清晰明白地了解算法，介紹本文中涉及的基本概念和原理。對于糾刪碼的基本概念本文將不再贅述，可參考文獻[4-5]。

以下給出一些矩陣譯碼算法所用到的線性代數定義及原理。

定義1左偽逆矩陣：矩陣A右乘矩陣B得到單位陣I，則稱B為A的右偽逆矩陣。當矩陣A行滿秩且行數小于列數時，右偽逆矩陣一定存在。

定義2零空間：零空間是指與矩陣的每個行向量正交的所有向量的集合。零空間基則是指零空間中一個線性獨立向量的最大集合。

假定G為大小為R×C的矩陣，為編碼理論中的生成矩陣。H為編碼理論中的偽逆矩陣且R≤C，當B為G的零空間基，U為G的右偽逆矩陣，X在大小C×(R-C)的二進制矩陣上變化時，其中Ok為半單位陣：

G·(U+(B·X))=Ok

(1)

式中：U+(B·X)在所有部分偽逆上運行，X是在U的每一列增加一個零空間向量。

在編碼理論中存在兩個重要等式，分別為D×G=T和T×H=0。其中D為編碼前元素向量，T為編碼后元素向量。由此可推出：

D×G×H==0

(2)

由式(2)即可看出H是G的零空間基，因此可以利用校驗矩陣來求生成矩陣的偽逆矩陣。

原理1由矩陣譯碼算法得來的偽逆矩陣U中，任意理論可恢復的數據元素對應U中的一個非零列，列中每個非零位置對應哪些數據元素與冗余元素，它們的異或和即為該理論可恢復數據元素。一個直接可讀的數據元素對應U中一個單位列(即只有一個1的列)。一個數據丟失事件(理論不可恢復數據)對應U中一個全零列。

證明令T代表編碼后包含所有元素的向量，T′代表丟失后的編碼向量，即丟失對應位置為零，很明顯。

D·G′=T′

(3)

丟失元素在G′中對應全零列。因此有:

T′·U=D·G′·U=D·Ok=D′

(4)

式中：D′的零元素位置對應Ok對角線上為零的位置，同時Ok對應偽逆矩陣U中的全零列。Ok中對角線上的非零位置對應D′中的非零元素，而Ok中對角線上的非零位置同時對應偽逆矩陣U中的非零列，由此偽逆矩陣U的每一行就對應D′中的每一個元素。同時，因為T′·U=D′，所以偽逆矩陣U中的每一列，每一個位置對應T中的一個元素，由此每列對應一個數據元素，且每一非零位對應一個已知可得的元素。

1.2 矩陣譯碼算法核心

矩陣譯碼算法的核心為偽逆矩陣U的構造，因此接下來描述偽逆矩陣構造的過程。首先定義一個丟失元素列表L，記錄丟失元素在D中的位置，H為校驗矩陣。

步驟一：構造一個方陣W，W=(U|H)，初始的偽逆矩陣U由一個單位陣和(R-C)行全0行構成。

步驟二：對于丟失元素列表L，另r表示丟失元素對應W中行向量，進行如下操作：

(1) 查找H中r行有1的列b，如果不存在，將U中b列對應有1的行置零，然后繼續下一個冗余元素。

(2)W中r行有1的每個列c，如果c≠b，那么將列b加到列c上。

(3) 將H中列b置零。

步驟三：利用所得U將丟失數據元素恢復出來。

1.3 矩陣譯碼算法分析

矩陣譯碼算法作為一種糾刪碼譯碼算法，可以用于任意糾刪碼，更適用于二元域的陣列碼。當其應用于陣列碼時，該算法有兩大優勢：(1) 是一種通用性的解碼算法，它可以適用于任意陣列碼解碼；(2) 可以恢復任意數據失效扇區。

矩陣譯碼算法可以用于所有陣列碼，例如：STAR碼[6]、EVENODD碼[7]、RDP碼[8]等。尋常的陣列碼譯碼算法是利用循環迭代的方式進行解碼，當一個節點中任意扇區失效時，都被認為是該節點失效，從而對整個節點進行恢復。但是隨著數據量的不斷增大，硬件不斷增多，某個節點中扇區丟失的現象越來越多。當重建整個節點時，也會重建那些不必要重建的扇區從而造成重復，增加不必要的計算量，因此針對隨機元素或扇區丟失的恢復也成為糾刪碼解碼的一個重要問題。矩陣譯碼算法就可以實現這一目標，可以恢復理論可恢復的任意扇區失效。可以達到這一目標的譯碼算法還有一個比較有代表性的，是文獻[3]中提出的歸并譯碼算法。歸并譯碼算法與矩陣譯碼算法的最大區別在于矩陣譯碼算法無需進行矩陣的求逆運算，計算的時間復雜度低，歸并譯碼算法仍然涉及矩陣求逆運算，出現單個錯誤時，譯碼時間可以接受，但是當有兩個及以上的錯誤時，譯碼的時間成本仍然很高。因此相比較來講矩陣譯碼算法在時間復雜度上要更優一點。

矩陣譯碼算法也存在缺點，就是當錯誤元素中包含有冗余元素時，不能直接求出冗余元素，而需要在求出數據元素后利用編碼計算出冗余元素。當出現冗余元素錯誤時，這個缺點也會在一定程度上影響計算的時間復雜度，因此如果可以在求解數據元素的同時將冗余元素求出，必將在一定程度上提高計算時間復雜度。

2 矩陣譯碼算法改進研究

上一節中對于矩陣譯碼算法進行了描述以及原理證明，又分別給出了算法的優缺點。本節中，針對矩陣譯碼算法的不足之處，提出本文的改進研究方案。該改進算法可以恢復任意理論可解的情況，減少了對于冗余元素的計算量，降低了計算時間復雜度。本節中，首先對改進算法步驟進行描述，并對其中冗余元素的求取進行正確性證明，最后根據情況舉出具體的實例。

2.1 改進算法描述

為了與平時編碼理論習慣相一致，在改進算法中，生成矩陣G采用縱向矩陣，校驗矩陣H采用橫向矩陣方式表示，因此偽逆矩陣變為右偽逆矩陣。將數據丟失元素列表記為L。以下描述本算法步驟：

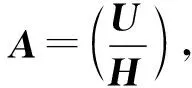
步驟二：判斷構成A的校驗矩陣H的右半部分是否為單位陣，若不是，通過校驗矩陣行與行間初等行變換即異或將其變為單位陣后進行運算，如下例：

RDP(4,3)的校驗矩陣如下：

由上式可看出RDP校驗矩陣的右半部分并不是校驗矩陣，因為進行初等行變換，將第一行與第二行進行異或并放置于第二行，則可得到單位陣，可得結果如下式：

步驟三：對工作空間A進行行變換也相當于求逆的過程，具體求逆過程在下面會進行描述；

步驟四：得出變換后的工作空間A即可恢復出丟失元素，A中一行代表一個數據元素，每行中非零位置代表已知可得的數據元素。

其中將工作空間A進行初等行變換求逆的具體步驟如下：

步驟一：對丟失元素列表L中的每個數據元素s，循環遍歷L中s，首先判斷數據元素s的類型，是屬于原始數據的還是冗余數據，若為數據元素繼續進行操作進入步驟二，若為冗余元素則跳過進行下一個元素的判斷；

步驟二：在校驗矩陣H中找s列為1的行h。如果不存在這樣的行h，那么將U中s列有1的行置零(說明此元素s理論上不可恢復)；

步驟三：若找到列表h后，如果L中沒有包含冗余元素，即沒有冗余元素丟失，那么就從找到的列表h中選擇最稀疏的一行(即漢明重量最小的一行)f，如果L中包含冗余元素，則將L中丟失的冗余元素對應行號從找到的列表h中去除后再在列表h中選擇最稀疏的一行f(為了保留丟失的冗余元素對應行的值，最后可以同時求出)；

步驟四：對于工作空間A中第s列為1的行E列表，如果E中每一個元素e≠f，那么將f與e相加(異或)并替換掉e；

步驟五：將構成工作空間的行H中第f行置零；

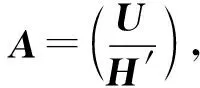
至此，對于算法改進的研究步驟基本描述完畢。最后得到的工作空間既可以恢復數據元素，又可以恢復校驗元素，也就是可以恢復所有理論上可恢復的情況。

2.2 正確性證明

本文提出的改進研究算法中保留了對于數據元素恢復的偽逆矩陣，同時生成了一個新的用于恢復冗余元素的冗余矩陣，用H′表示。下面將對冗余矩陣進行正確性證明。

校驗矩陣是用來檢驗碼字是否正確的一種矩陣，它的每一列代表一個元素位置，每一行代表一個冗余元素，同時也是一個方程式(每一行中所有非0位置進行異或后結果為0)。上面所提到的冗余矩陣便是由校驗矩陣變換得來。

原理2由本文的改進算法得出的冗余矩陣，它的非零行代表一個理論上可恢復的冗余元素，這一行中每個非零位置對應的元素異或和即為該行對應的冗余元素的值。每一個全零行代表一個已知可讀的冗余元素。

證明校驗矩陣的每一行異或結果均為零，因此將校驗矩陣進行初等行變換后并不會改變此性質。而根據異或邏輯運算，如果兩個值不相同，異或結果為1；如果兩個值相同，則異或結果為0。當進行求冗余矩陣的步驟時，將丟失冗余元素對應列置零后，冗余矩陣中每一個非零行上其余元素的異或和應等于丟失元素的值，由此即可證明出原理即冗余矩陣的正確性。下面將給出一個例子說明。

以STAR(6,3)的校驗矩陣為例，其校驗矩陣如下：

校驗矩陣的每一行都代表一個冗余元素，STAR(6,3)的冗余元素為(P0,P1|Q0,0,Q1,0|Q0,1,Q1,1)。假設丟失的冗余元素為P1，那么在算法的最后將P1對應的列也就是第7列置零，則第2行剩余非零位置所應對的元素異或和即為P1的值，公式如下：

d1,0+d1,1+d1,2=P1

2.3 具體實例

上一小節中證明了該算法的正確性，本小節將采用典型的實例來進一步分析和說明本算法。

例1：以EVENODD(5,3)[7]為例，將磁盤數據展開來排成一個行向量，可以寫為T=(d0,0,d1,0|d0,1,d1,1|d0,2,d1,2|P0,P1|Q0,Q1)，此時假設丟失元素為d0,0、d0,1、P1、Q0，則丟失元素列表為L=(0,2,7,8)。

首先構造一個10×10的工作單元A：

(5)

判斷構成工作單元的校驗矩陣右半部分是否為單位陣，由式(5)可以看出符合條件，那么繼續進行操作，循環遍歷丟失元素列表s。當s=0時，0屬于數據元素，所以在H中找第0列為1的行h，可以找到h=6,8。因為8也是丟失元素，將其排除，選擇h=6。將第6行分別加到第0行，第8行后，第6行置零，結果所得工作單元A為：

(6)

繼續當s=2時，2屬于數據元素，所以在H中找第2列為1的行h，可以找到h=8,9。因為8為丟失元素，將其排除，選擇h=9。將第9行分別加到第0行，第2行和第8行后，第9行置零，結果所得工作單元A為：

(7)

當s=7時，7屬于冗余元素，所以跳過；當s=8時，8屬于冗余元素，所以跳過。丟失元素列表循環完畢，將7、8列置零。最終所得工作空間A為：

(8)

工作單元A中，上半部分為求解數據元素的偽逆矩陣，下半部分為求解冗余元素的冗余矩陣。因此可恢復出丟失的數據元素與冗余元素d0,0、d0,1、P1、Q0。具體公式如下：

(9)

例1：以RDP(4,3)為例，將磁盤數據展開來排成一個行向量，可以寫為T=(d0,0,d1,0|d0,1,d1,1|P0,P1|Q0,Q1)，此時假設丟失元素為d0,0、d0,1、P0、P1，則丟失元素列表為L=(0,2,4,5)。

首先構造一個8×8的工作單元：

(10)

判斷構成工作單元的校驗矩陣右半部分是否為單位陣，由式(10)可看出，不符合條件，因此將第5行加到第6行，使其變為單位陣：

(11)

開始循環遍歷丟失元素列表。當s=0時，尋找H中第0列為1的行h，可得h=4,6。因為4同樣為丟失元素，拋棄掉，選擇h=6。將第6行分別加到第0行和第4行后，第6行置零。當s=2時，在H中找第2列中為1的行，h=(4,7)，但是因為4在L中，所以排除4，選擇h=7，選定后將第7行加到0、4行，然后第7行置零。當s=4時，4為冗余元素，跳過；當s=5時，5為冗余元素，跳過。丟失列表元素循環完畢，將4、5列置零，最后可得工作單元式(12)：

(12)

工作單元A中，上半部分為求解數據元素的偽逆矩陣，下半部分為求解冗余元素的冗余矩陣。因此可恢復出丟失的數據元素與冗余元素d0,0、d0,1、P0、P1。具體公式如下：

(13)

3 實驗分析

就糾刪碼的性能而言，關鍵還在于它的編解碼，本文主要研究的是糾刪碼的解碼算法。

陣列碼是一種僅通過異或運算構造的碼制，它本身的解碼算法是利用循環迭代來進行解碼。當一個條塊中的一個元素丟失即認為是整個條塊乃至整個磁盤的丟失，恢復時會重建整個磁盤，且每種陣列碼的原始解碼均不相同。文獻[4]提出一種恢復隨機數據元素的算法——矩陣譯碼，利用生成矩陣的偽逆理論重建數據元素，適用于任意的糾刪碼，但是卻不能同時恢復冗余元素。而Tang在文獻[3]中提出一種歸并譯碼算法，通過對校驗矩陣分塊并求逆來重建磁盤數據元素，可以同時恢復數據元素和冗余元素，但是這種算法需要計算逆矩陣，增加了計算復雜度，效率不高。本文提出的改進解碼算法是基于矩陣譯碼算法的改進，可以恢復理論上可以恢復的任一情況，包括同時恢復數據元素與冗余元素。因此本節將使用幾種不同的糾刪碼譯碼方法作為容錯方案構建存儲仿真系統，在存儲仿真系統中對失效數據進行重構。構建存儲仿真系統所使用的語言平臺為Python。構建存儲仿真系統所用到的計算機主要配置為：CPU Inter Core i5-6200U，內存8 GB，磁盤容量250 GB。

對于EVENODD碼，一般常用的解碼算法為循環迭代的解碼算法，因此我們在仿真存儲系統中首先對EVENODD進行編碼，素數選取5。模擬數據丟失事件，然后利用幾種不同的譯碼算法對其進行比較分析。設置文件存儲的塊大小為10 240 B，對于不同文件的大小，分別利用四種解碼算法進行對比實驗分析。針對不同尺寸文件的單節點失效和雙節點失效，其中雙節點失效模擬節點0和節點5失效。

實驗1在以上所描述的實驗條件下，首先對于歸并譯碼和改進方法進行對比，時間效率對比圖如圖1和圖2所示。圖1為單節點失效的時間效率對比圖，圖2為雙節點時間效率對比圖。在單節點失效時，歸并譯碼與改進算法相差并不是很多，這也說明了歸并譯碼方法在單節點失效時效率不低。但是從圖2可以很明顯看出文獻[3]的歸并譯碼效率遠不及改進方法的時間效率。同樣的前提下，當發生兩個節點失效時，歸并譯碼幾乎是改進方法的1.5倍。之后隨著文件尺寸的增大，歸并譯碼有可能呈現指數級的增長，而本改進譯碼方法隨著文件尺寸的增大，時間消耗呈直線性增長。

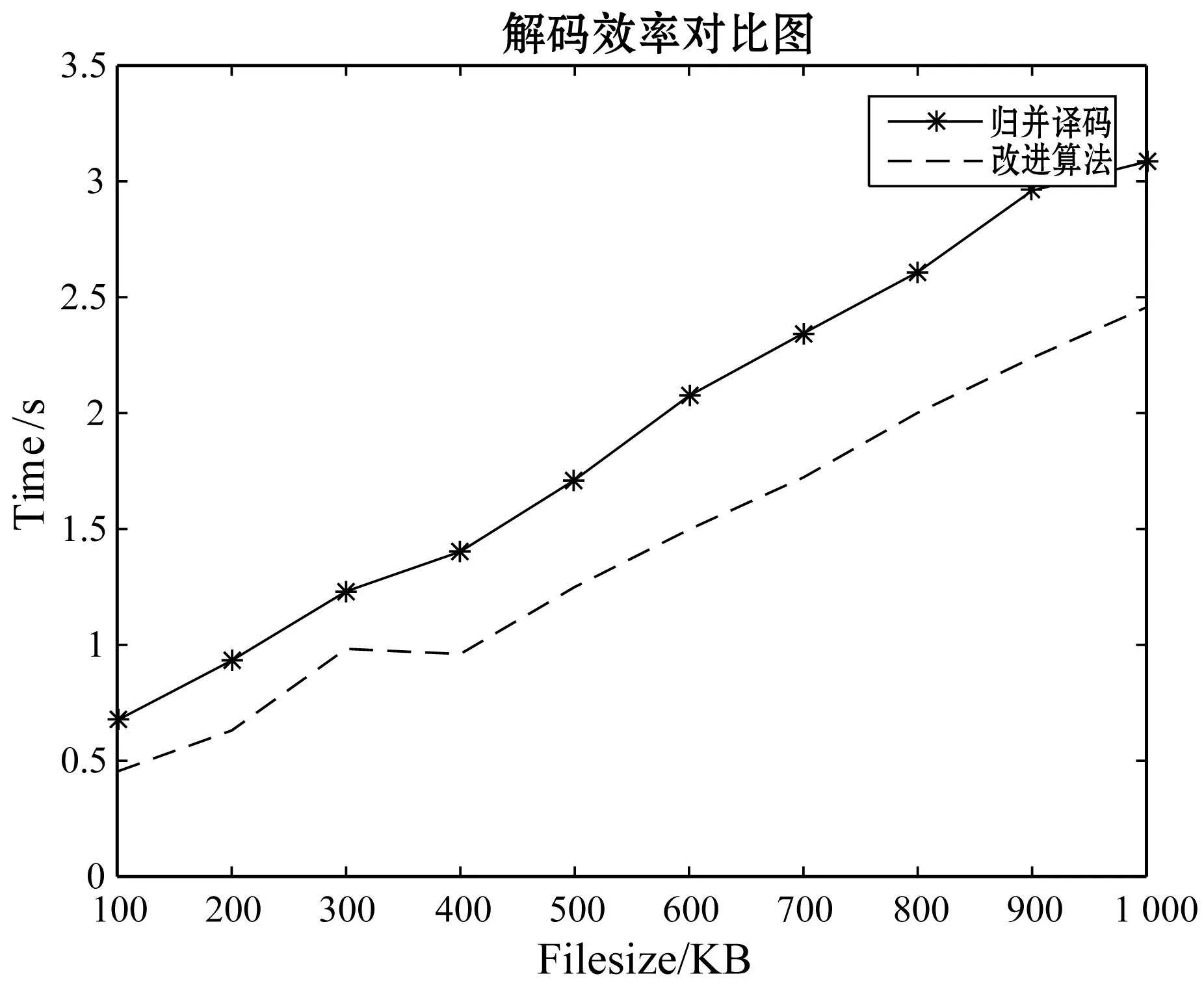
圖1 單節點失效譯碼時間對比圖

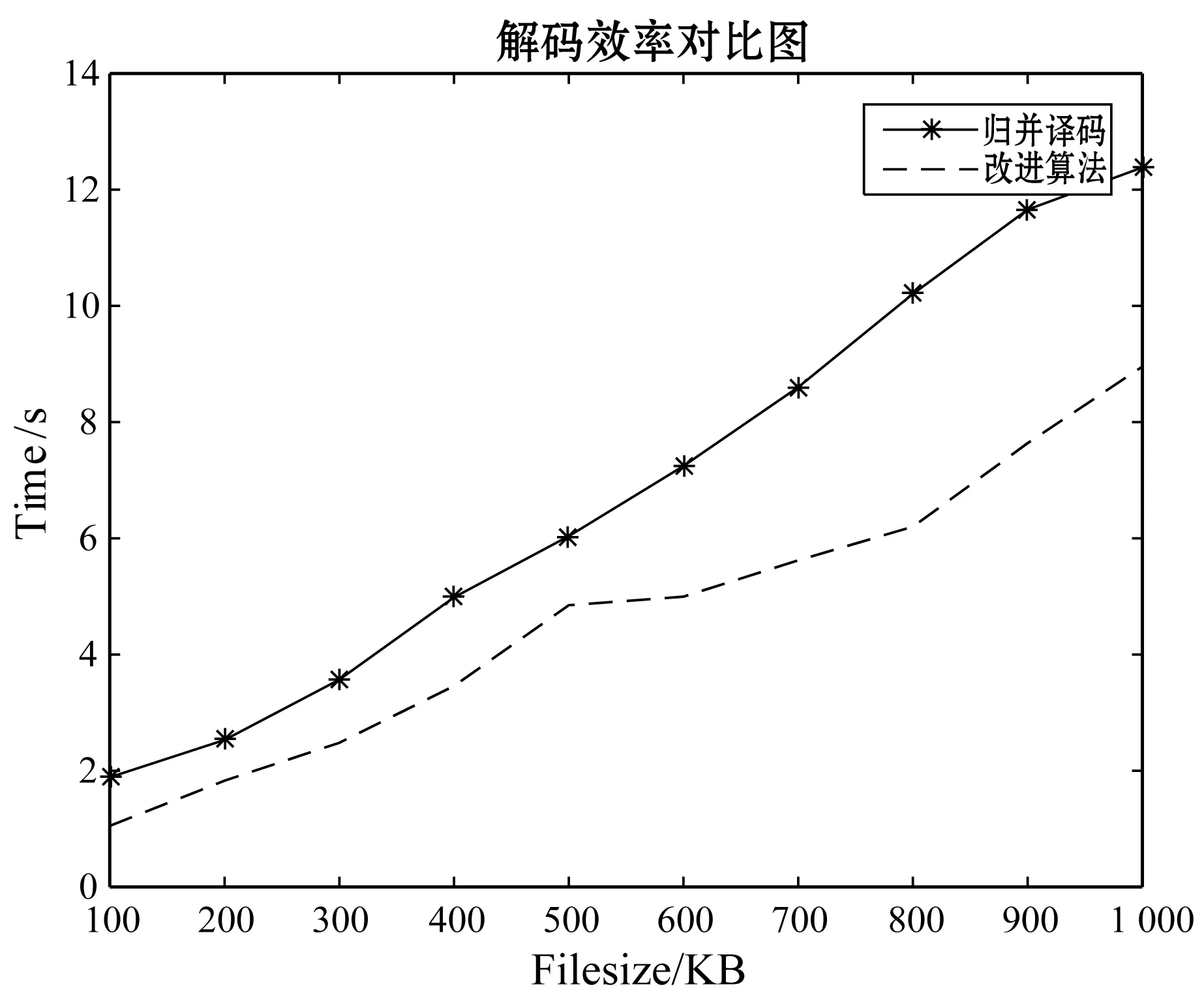
圖2 雙節點失效譯碼時間對比圖

實驗2在本節剛開始所描述的實驗條件下，對矩陣譯碼方法和本改進譯碼方法進行時間效率的對比，對比時間效果圖如圖3和圖4，圖3為單節點失效時的時間對比圖，圖4為雙節點失效的時間對比圖。從圖3可以看出，單節點時，因為只恢復一個數據節點，因此并不能體現出改進的優點。從圖4雙節點丟失的對比圖可以看出兩者的效率相差雖不多，但還是有一定的差別，本改進算法的時間消耗始終比矩陣譯碼方法的效率高，也說明了同時恢復數據元素和冗余元素比先恢復數據元素再根據編碼恢復冗余元素效率要高。

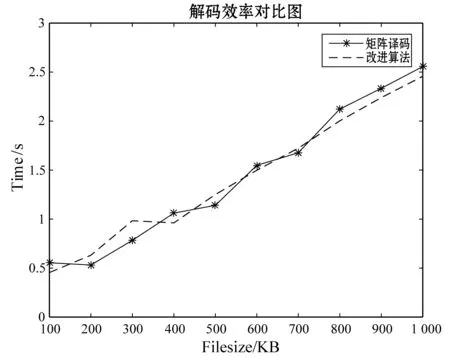
圖3 單節點失效譯碼時間對比圖

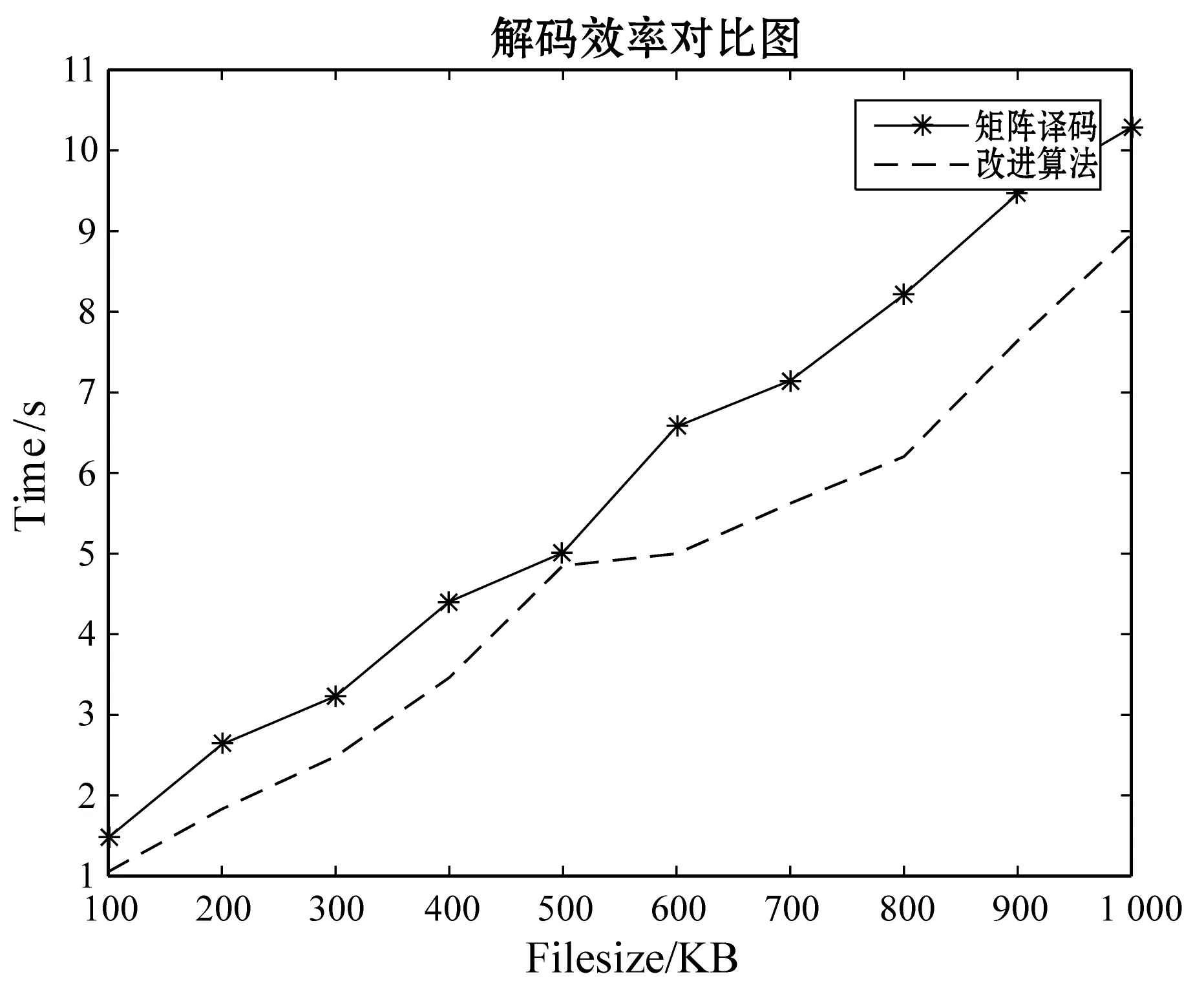
圖4 雙節點失效譯碼時間對比圖

實驗3仍然利用與前兩個實驗相同的實驗條件，對循環迭代法和改進方法進行時間效率對比，對比圖如圖5和圖6，圖5為單節點失效的時間對比圖，圖6為雙節點失效的對比圖。兩張圖都可以很明顯地看出循環迭代法的效率要比改進方法的效率高，但是相差不多。從另一個方法看，改進方法可以是對于不同節點中隨機扇區進行理論可行的恢復，而循環迭代法只能針對節點進行恢復，當一個節點中某一個扇區丟失時，必須要恢復整個節點，增加了很多不必要的計算量。目前在存儲系統中，發生扇區失誤的概率很高，因此，兩者平衡下，改進方法要相對好一些。

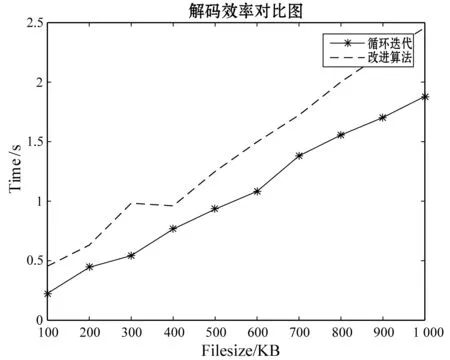
圖5 單節點失效譯碼時間對比圖

圖6 雙節點失效譯碼時間對比圖

從以上三個實驗可以很明顯看出，本文提出的改進算法的計算效率比較優異且在各方面的性能比較均衡。

實驗4為了證明本改進算法的通用性，利用與上面三個實驗相同的實驗條件，將改進方法應用于RDP碼中，模擬雙節點丟失的事件，并與其余三種譯碼方法進行對比。時間效果對比圖如圖7所示，也從另一方面驗證了上述三個實驗結果的正確性。

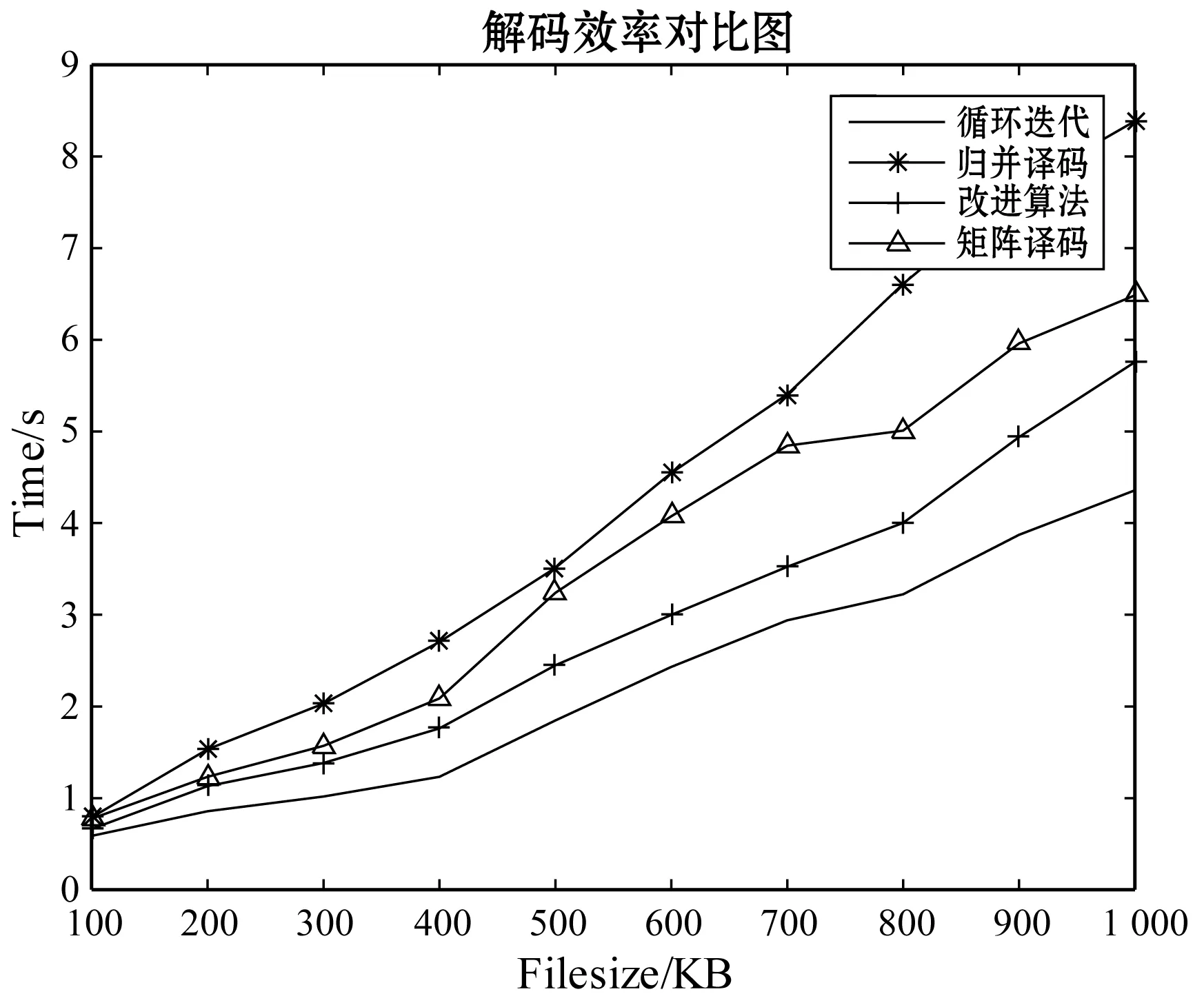
圖7 RDP雙節點失效譯碼時間對比圖

4 結 語

針對糾刪碼解碼算法，本文首先介紹了一種通用性的解碼算法——矩陣譯碼，在保留了原算法的優勢下，對其不足之處進行改進研究，最后在仿真存儲系統中進行實驗數據分析，可以看出確實在性能中有所改變，可以廣泛應用于隨機扇區丟失的場景。本文提出的這種改進算法目前是運行在二進制矩陣上的針對陣列碼的運算，以后改進研究可以將此算法推廣至非二進制上進行解碼運算。