“一帶一路”下基于兩階段模型的無水港選址研究

梁承姬 黃博峰

(上海海事大學物流研究中心 上海 201306)

0 引 言

2013年，中國提出亞歐經濟整合的藍圖，即 “一帶一路”。“一帶一路”的提出，一方面加快了我國中西部運輸基礎設施的建設，另一方面促進了我國與亞洲、歐洲之間運輸業的發展。“一帶一路”建設目前處于起步階段，要實現亞歐運輸的一體化需要考慮多式聯運的有效對接。無水港作為其中重要一環，日益受到人們的重視。

國內外學者對“一帶一路”和無水港/樞紐港已有諸多研究。蔣雪瑩等[1]結合“一帶一路”背景下的中歐鐵路運輸體系，考慮顧客的選擇行為和基礎設施處的擁擠與等貨效應，建立了混合整數規劃模型，解決了社會福利最大化時的鐵路貨運集拼中心的最優選址。高亞平[2]在明確了一帶一路的運輸網絡后進行了環路分析，建立了運輸費用模型，找出中國至各個路段的經濟路線。文獻[3]提出了一種評估無水港選址優先權的新方法，通過考慮反饋和影響無水港設施的因素建立評估模型，解決了無水港選址優先權評估問題；邵靜靜[4]基于評價指標體系方法，通過建立無水港選址多目標模型解決無水港選址問題；王瑩等[5]通過建立無水港發展潛力評價指標體系，運用模糊層次分析法評價晉江無水港發展潛力；文獻[6] 通過建立兩級加權動態圖的數學規劃模型，解決了無水港在多式聯運下集裝箱流運輸問題；文獻[7]認為無水港在多式聯運系統中存在優化的空間，提出了混合整數規劃模型，解決了無水港聯運系統中車輛運輸的最佳路線和調度問題；梁承姬等[8]提出在集裝箱多式聯運的基礎上，加入了成本折扣系數，并用改進遺傳算法求解無水港選址問題。

綜上可知，已有研究文獻多數是基于評價指標體系或是選址優化的獨立研究，沒有考慮將兩種研究方法結合為一體。據此，本文將這兩種方法相結合，提出兩階段模型的無水港選址以及相應的求解方法，使無水港選址考慮因素更全面、科學。第一階段借助模糊C-均值聚類分析選出候選城市，第二階段在候選城市中進行選址優化，得出最優的選址結果。為驗證兩階段模型的有效性，同時，本文又直接用單一的選址優化模型對算例進行求解，并將兩者的求解結果對比，證明本文使用的方法更加有效。

1 問題描述

無水港根據距離依托母港的遠近，可以分為近距離、中距離、遠距離無水港。本文研究的是遠距離無水港選址問題。假設在中歐、中國-中亞這兩條支線的運輸路線附近有眾多的貨源城市，這些貨源城市需要將貨物運往中國的某個沿海母港，如圖1所示。獨立地將貨源城市的貨物運往目的地會耗費較大的運輸成本，而眾多城市貨物的聯合運輸可以產生聚集效應，降低成本，因此可以考慮在眾多的貨源城市中選擇合適的城市建立無水港。本文考慮了貨物的多式聯運，聯合運輸中無水港作為銜接多種運輸方式的中轉站，通過其選址和運輸方式選擇的決策，可降低聯合運輸的成本、提高運輸效率。

圖1 運輸路線圖

綜合考慮以上問題描述，通過建立兩階段模型解決上述問題。第一階段根據一系列影響因素對貨源城市的發展現狀和潛力進行評估和篩選，選出適合作為無水港候選的城市。第二階段，在上一階段的基礎上，通過建立包括運輸成本、無水港建設成本、換裝成本的總成本最小的目標函數，找出成本最低的無水港位置。

2 階段1——候選無水港篩選模型

2.1 無水港選址評價指標體系

本節在綜合考慮影響選址決策的整體因素及成功無水港必備條件的基礎上，為篩選候選城市建立指標評估體系包括定性和定量指標，具體指標因素見表1所示。

其中交通擁擠度(x7)的指標從0～10, 指數在0～2為暢通、2～4為基本暢通、4～6為輕度擁堵、6～8中度擁堵、8～10為嚴重擁堵。政策傾向(x8)表示政府的支持傾向，1為支持，0為否。

2.2 評估求解方法

本文采用的FCM方法常用于具有較多影響因素以及影響未確定的目標進行聚類，對處理具有不確定性和模糊性的無水港評估因素具有優勢。

本文假設有n個貨源城市(x1,x2,…,xk,…,xn)根據指標p被聚類成c(2≤c≤n)個子集，FCM的目標是最小化非相似性目標函數J(U,V)。

(1)

約束條件：

(2)

式中：J表示FCM的目標函數；U表示隸屬度矩陣集合；V表示聚類中心集合；dik表示xk與聚類中心的子集i的距離，即dik=‖xk-vi‖；m表示權重指數。

特別地，FCM主要分為以下六步：

步驟1: 確定類別c和加權指數m的數量。

步驟2: 通過從[0,1]中選擇統一的數，初始化隸屬度矩陣U(0)=(uik(0))。

步驟3: 計算聚類中心vl，公式如下：

(3)

步驟4: 修正隸屬度矩陣U(l)并計算J(l)，公式如下：

(4)

(5)

dik=‖xk-vi‖

(6)

3 階段2——無水港選址模型

本節將無水港選址優化問題轉化為多式聯運的物流運輸網絡問題來解決, 如圖2所示。運輸方式分為兩種:第一種是直接從貨源城市運往母港，即貨源城市-母港；第二種是途經無水港，即貨源城市-無水港-母港。本節考慮了多式聯運，從貨源城市運往母港的貨物可能會發生分離，通過不同的運輸方式或途經不同的無水港到達母港。同時，一個貨源城市的貨物可能會分離運往不同的無水港。

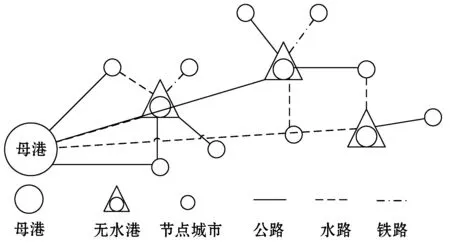
圖2 途經無水港的多式聯運

3.1 模型假設及參數符號說明

無水港選址模型假設如下：

1) 物流運輸網絡中每個貨源城市都有三種運輸方式可供選擇：公路、鐵路、水路；

2) 每段運輸只能選擇一種運輸方式；

3) 貨源城市數量、貨物運輸需求已知；

4) 運輸費率、運輸距離及轉換費率已知；

5) 無水港建設成本已知,無水港個數定為4；

7) 貨物到達無水港后換裝時產生的等待時間忽略不計。

基于模型假設，構建無水港選址模型如下：

目標函數：

(7)

約束條件：

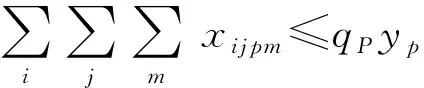
(8)

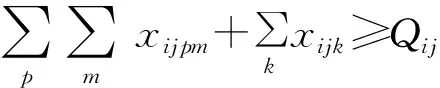
(9)

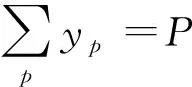
(10)

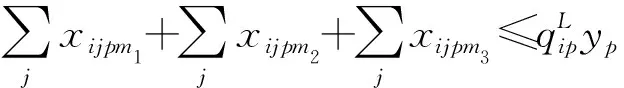
(11)

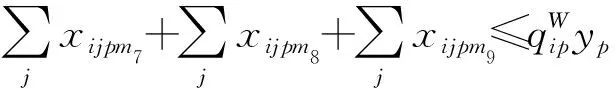
(13)

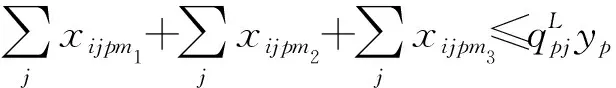
(14)

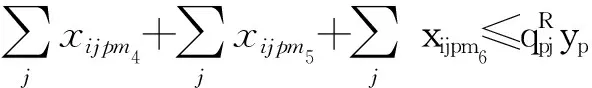
(15)

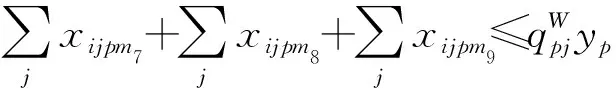
(16)

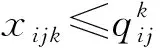
(17)

xijpm≥0 ?i∈OS?j∈OD?p∈OPm∈M

(18)

yp∈{0,1} ?p∈OP

(19)

3.2 遺傳算法求解

該模型的離散決策變量代表無水港的容量約束和選址。本文提出以下有效的全局尋優方法，即遺傳算法，以獲得該模型最優解。

1) 編碼 染色體用三段式的編碼方法來描述選址。第一段采用二進制編碼，表示是否選擇候選貨源城市作為無水港，1表示選該城市作為無水港候選，0表示未被選中。第二段表示第一段中城市的對應分配關系，若城市i分配給無水港p，則基因位值為p。第三段表示對應每個城市的運輸方式，1、2、3、4、5、6分別表示上文提到的m1、m2、m3、m4、m5、m6。

下面以表2為例。染色體第一段中，1表示該在節點建立無水港，0表示該節點不建無水港，在節點2、6、8、13建立無水港；第二段的分配關系：節點1、3、7、10、11、14→母港，節點2、9→無水港(節點)2→母港，節點5、6→ 無水港(節點)6→母港，節點8→水港(節點)8→母港，節點12、13→無水港(節點)13→母港。第三段中，節點1、3、7、10、11、14分別以m6、m2、m4、m9方式直接運到母港，其余分別以對應方式運輸，比如：節點2通過m3方式運輸，節點9通過m1方式運輸。

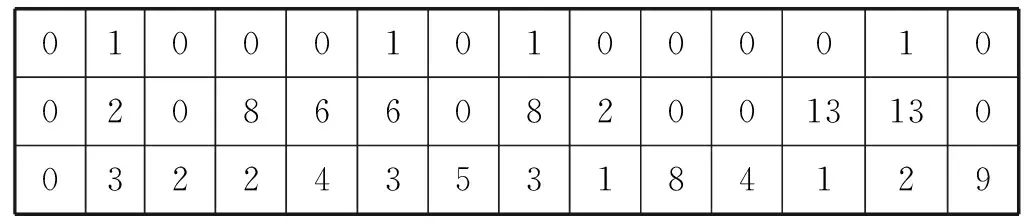
表2 染色體編碼

2) 適應度函數 適應度函數被定義為目標函數的倒函數，即：

(20)

3) 選擇操作 運用隨機遍歷的的方法，并綜合運用最優保優策略。

4) 交叉操作 本文采用基于位置的交叉方法。子代C1、C2、C3得到父代P2、P1、P3的第一個n1基因，下一個n2-n1基因分別從P1、P3、P2得到，其余的|N|-n2基因分別從P3、P2、P1得到。圖3說明了第一段染色體片段的交叉過程，其余兩段操作同理。

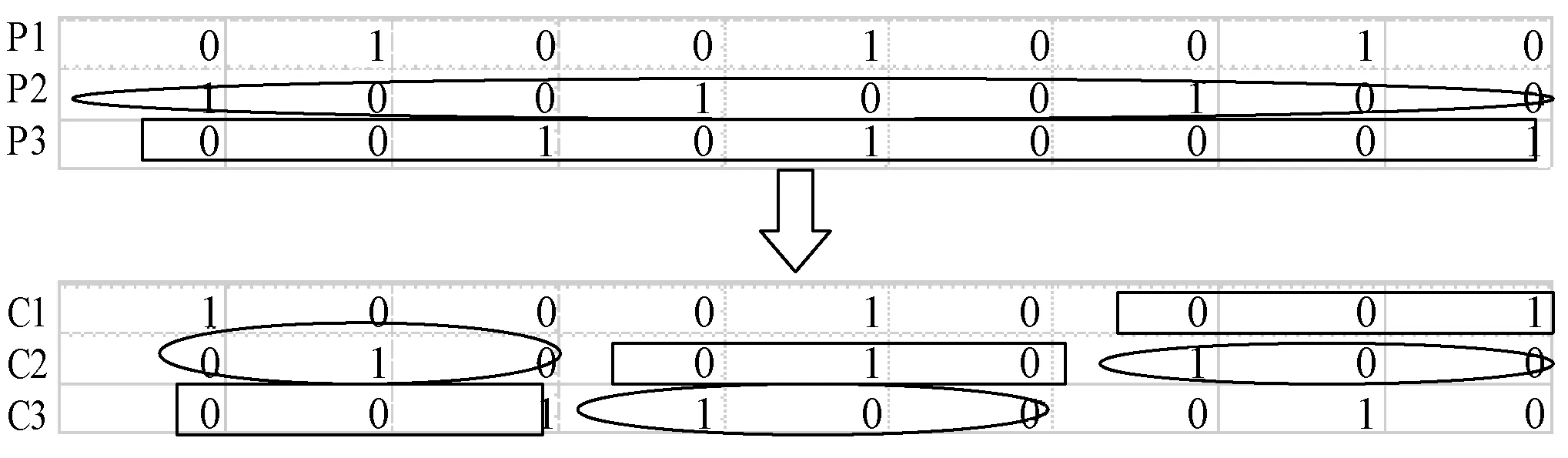
圖3 交叉操作示意圖

5) 變異操作 在滿足無水港和路徑容量約束的情況下，隨機將兩個城市對換。此處選取染色體的第一段，應用均換位異策略進行變異操作，如圖4所示。

圖4 變異操作示意圖

6) 終止原則 當代數超過最大迭代代數時，算法終止。

4 算例分析

本文以上海港為母港，緊密聯系“一帶一路”經濟走廊，以中國-中亞-歐洲這條主線上的貨源城市為備選研究對象，優先考慮區域經濟較發達地區，因此選取了蘇州(1)、杭州(2)、鄭州(3)、西安(4)、蘭州(5)、呼和浩特(6)、敦煌(7)、烏魯木齊(8)、杜尚別(9)、撒馬爾罕(10)、多哈(11)、伊斯坦布爾(12)、莫斯科(13)、安曼(14)、圣彼得堡(15)、安卡拉(16)、德黑蘭(17)、柏林(18)、杜伊斯堡(19)、法蘭克福(20)、巴黎(21)、馬賽(22)、耶路撒冷(23)、哥本哈根(24)這24個城市進行兩階段的無水港選址問題研究。

4.1 階段1——候選無水港篩選

在本階段中，選取了24個城市作為無水港候選城市。模型的參數假設設置如下：

1) 城市被分成4類，即c=4；

2) 基于聚類有效性分析，加權指數m=2；

3) 終止公差為：εu=1e-6。

FCM通過MATLAB的聚類分析，可以得到24個城市的Cluster Centre以及Cluster Membership，計算數據如表3、表4所示。

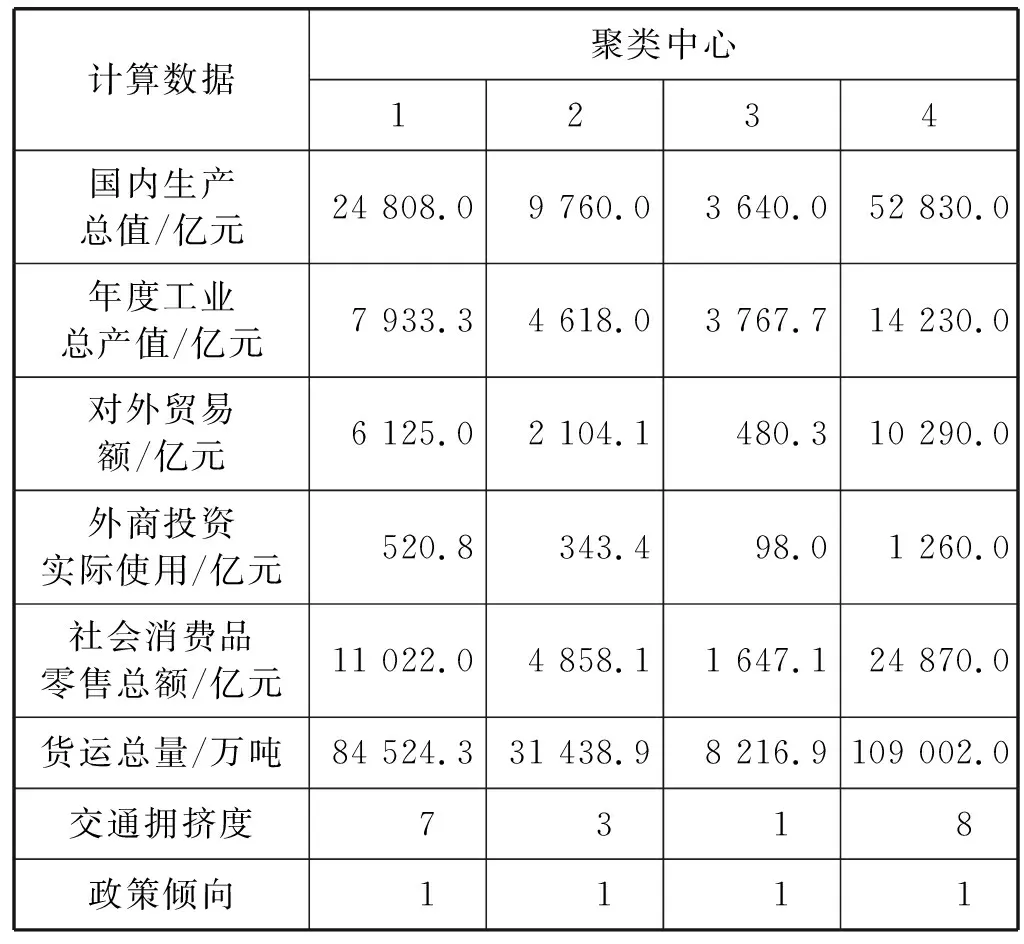
表3 最終聚類中心

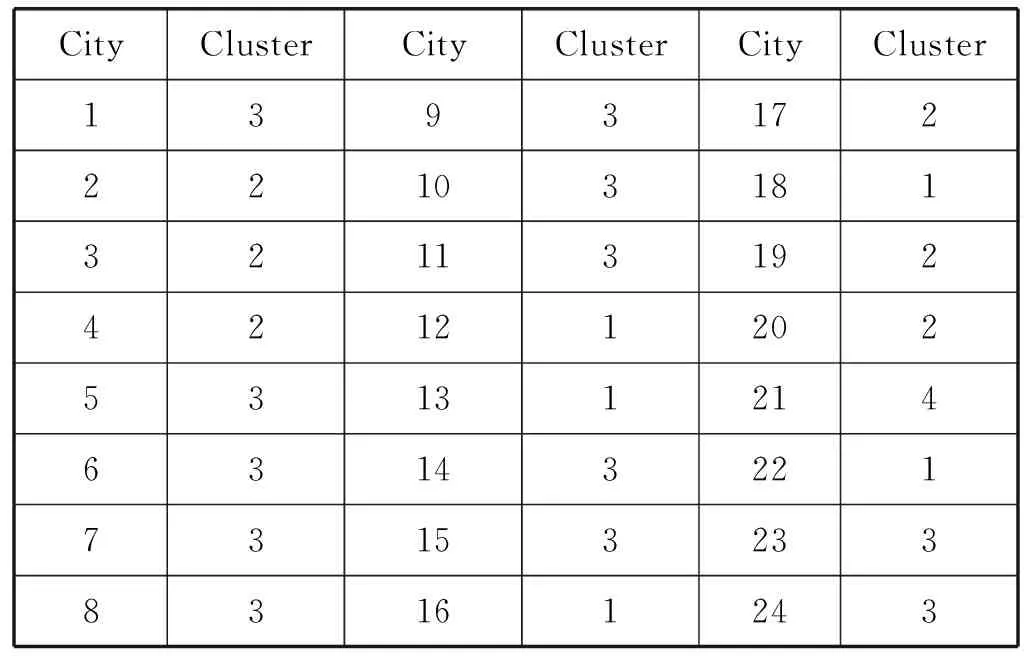
表4 聚類隸屬度

表4結果表明，類別1有4個城市、類別2有7個城市、類別3有12個城市、類別4有1個城市。類別1代表最發達的城市，最適合作為無水港的選址。由于發達城市的交通擁堵，也應該考慮類別2中的城市。同時，由于欠發達城市的建設成本低，交通便利,在中國、中亞、歐洲這三個地區各再選一個，即在類別3選三個城市作為無水港選址。因此，獲得14個城市作為潛在無水港的選址。最后,在第二階段中做進一步研究，這14個城市包括蘇州、杭州、鄭州、西安、伊斯坦布爾、莫斯科、安曼、安卡拉、德黑蘭、柏林、杜伊斯堡、法蘭克福、馬賽、哥本哈根。

4.2 階段2——無水港選址

本階段將第一階段中最終選出的14個城市為候選城市，并以其作為無水港備選節點進行研究，上海港(0)為母港。通過分析這14個城市周邊產業及經濟情況，確定其貨運量分別為：370 000噸，500 000噸，400 000噸，50 000噸，250 000噸，360 000噸，645 000噸，45 000噸，40 000噸，40 000噸，4 560噸，356 300噸，42 100噸，47 300噸。表5、表6給出了備選城市的相關數據，由于數據量大，故僅給出部分數據。由于各國的運輸標準存在差異，統一采用中國標準：鐵路運費0.3元/噸公里，水路運費0.2元/噸公里；公路換裝1.8元/噸，鐵路換裝2.1元/噸，水路換裝2元/噸。

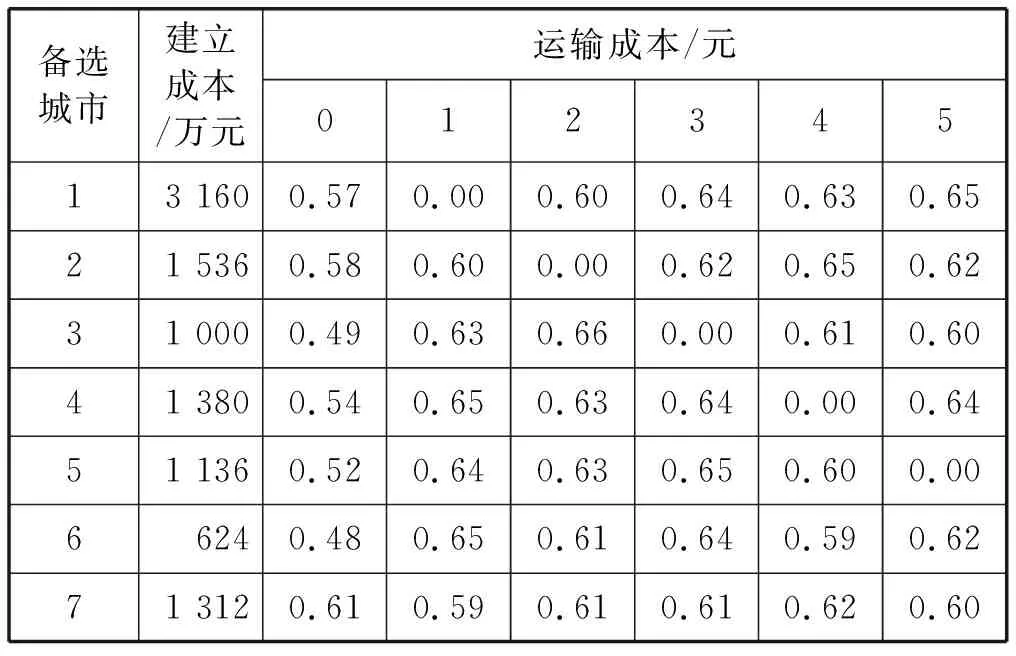
表5 無水港建立成本以及城市之間通過公路運輸的貨物單位運輸成本

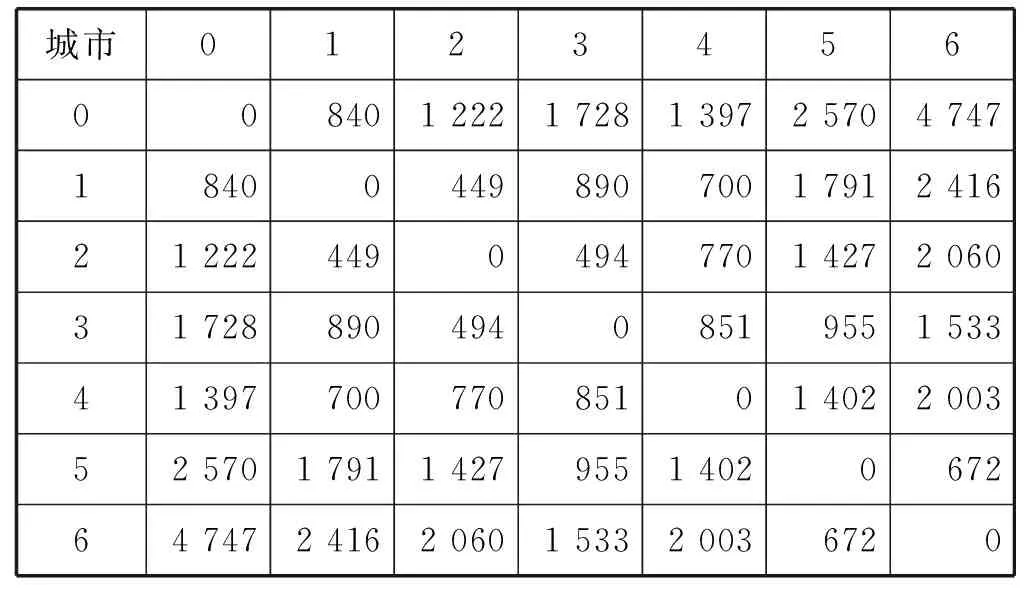
表6 城市與城市之間的距離 km

模型的參數輸設置如下：

種群規模popsize=200，最大迭代次數MAXGEN=500，交叉概率Pc=0.9，變異概率Pm=0.01。

4.3 結果分析

通過使用遺傳算法求得，總成本為201 016 469.62元。最終方案為：在節點3、6、9、12建立無水港。運輸路線的分配關系如表7所示。

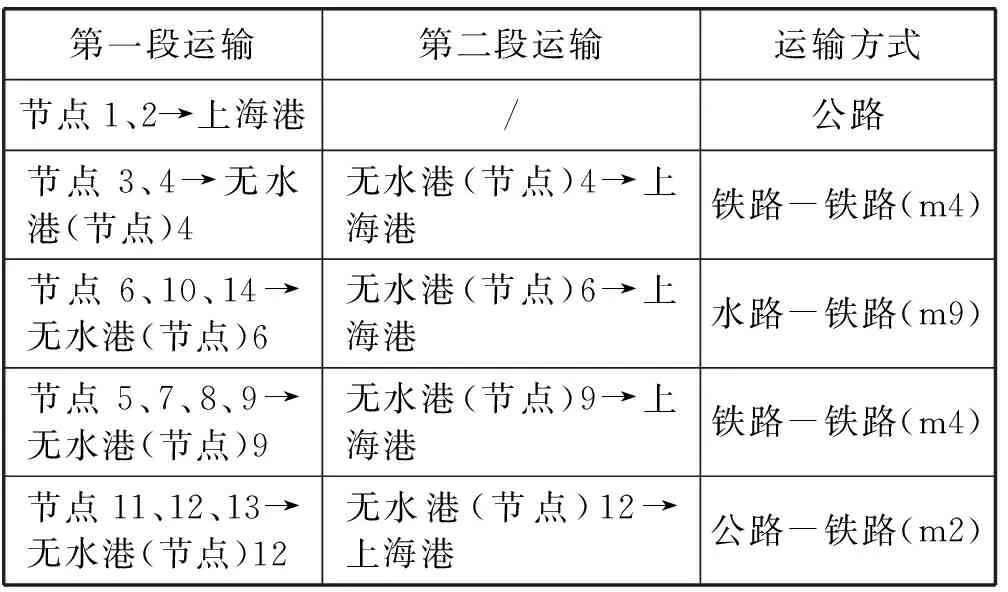
表7 運輸路線分配及運輸方式

如圖5所示，最優解在接近300代時就已經趨于穩定。為了驗證兩階段模型的有效性，跳過第一階段，直接對24個城市進行無水港選址，求得最終的目標函數值為237 903 527.06元，而運算時間為12.24 s。通過將兩階段法獲得的近似最優解和直接法獲得的近似最優解相比，結果顯示兩階段法的目標結果更優，且求解速度上有優勢，證明了本文設計的兩階段模型是有效的。

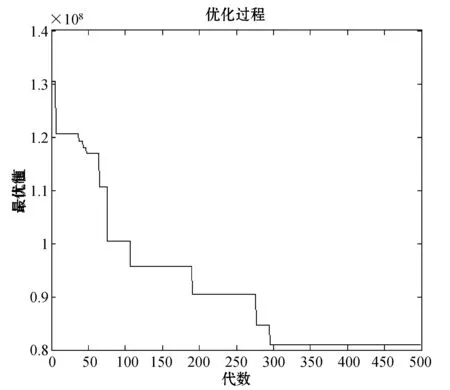
圖5 遺傳算法求解收斂圖

表8顯示，兩階段法得出的無水港建設成本、運輸成本、換裝成本各占總成本的24.4%、62.4%、13.2%。直接法得出的無水港建設成本、運輸成本、換裝成本各占總成本的27.9%、64.4%、7.7%。與直接法相比，本文建設成本下降了3.5%，運輸成本下降了2%，換裝成本提高了5.5%。對比結果表明，本文所用的方法更為經濟。

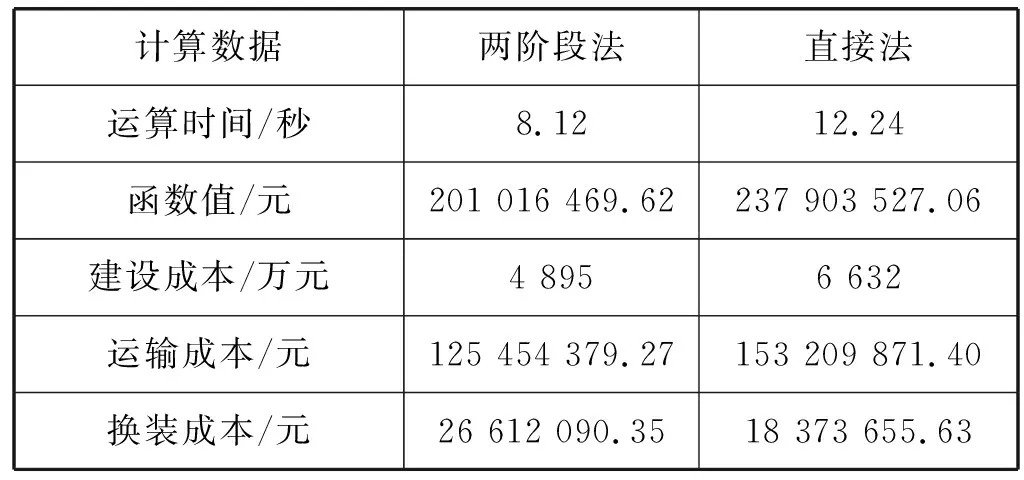
表8 兩種方法對比

5 結 語

本文在“一帶一路”背景下對無水港選址問題進行了研究，創新性地將無水港指標評價與選址優化方法結合運用，建立了兩階段模型的無水港選址模型，設計了模型求解算法解決問題。第一階段建立指標評價體系篩選無水港選候選城市，第二階段建立了包括運輸成本、無水港建立成本、換裝成本的目標函數，并利用遺傳算法來確定無水港的選址問題。算例應用分析表明，本文構建的兩階段法通過逐步篩選和優化，滿足了貨源城市的運輸需求，并且大大降低了總成本，與直接選址法相比，總成本降低了15.5%，驗證了兩階段模型的有效性和合理性，以期為“一帶一路”建設中的無水港選址研究提供理論參考和實踐指導。