基于差分進化算法的船舶能量管理系統優化策略

楊澤鑫，肖健梅，王錫淮，鄧軍

上海海事大學物流工程學院，上海201306

0 引 言

全球船舶市場的激烈競爭導致行業內需要性能更好的船舶能量管理系統來降低船舶運行成本［1］。而船舶大型化和船舶數量的不斷增加，則使得海上溫室氣體排放量不斷上升。近年來，溫室效應不斷加劇，造成了一系列嚴重后果。這使得世界各國對環境保護越來越重視，船舶的節能減排和可持續發展問題受到廣泛關注［2］。因此，在優化船舶能量管理系統時，既要考慮運行經濟性，又要考慮環保性［3-4］。

針對這一問題，已有不少學者進行了研究。Michalopoulos等［5］研究了含有軸帶發電機的能量管理策略，結果表明，軸帶發電機的使用可以降低船舶動力系統的運行成本和溫室氣體排放量。Shang等［6］提出了一種將發電調度、負荷管理（推進力負載—巡航速度）和儲能系統（ESS）調度相結合的全電力船舶能量管理系統，采用非支配排序遺傳算法（NSGA-II）對柴油發電機組的運行進行優化，大量仿真結果證明了該方法的經濟性和環保性。Chen等［7］通過研究基于負載功率傳輸模型的能量管理策略，提出了使得電站波動最小的性能指標，并采用粒子群算法（Particle Swarm Optimization，PSO）尋優，完成了系統電站和儲能元件之間的能量分配。Tsekouras等［8］提出了一種含有可再生能源和儲能系統的能量管理策略，并從經濟性角度對含有光伏發電和儲能系統的船舶電力系統的邊際成本進行了分析。但以上學者均是對新型船舶電力系統進行研究，忽略了廣泛應用的經典船舶能量管理系統的優化問題。

本文將運用差分進化算法（Differential Evolu?tion，DE）研究經典船舶能量管理系統的優化問題。擬以某客渡船為研究對象，在總負載、電力服務負載、推進力和船舶航速等預測數據已知的情況下，考慮發電機和柴油機的燃油消耗率（FC）曲線、電力系統運行限制以及溫室氣體排放量約束，運用差分進化算法、粒子群算法、遺傳算法（Ge?netic Algorithm，GA）優化調度策略，對船舶航速、發電機組啟停狀態、發電機組功率分配進行優化調度，通過多種方案的比較，證明差分進化算法對本問題的有效性。

1 船舶能量管理系統的數學模型

1.1 目標函數

船舶能量管理系統的優化問題是在滿足系統運行約束的條件下對船舶航速、發電機組啟停狀態、發電機組功率分配進行優化調度。

其目標函數為

式中：C為系統總運行成本；Ce為電力服務系統的總運行成本；Cpr為推進系統的總運行成本。運行成本的計量單位為貨幣單位（monetary unit，m.u.）。

對于電力服務系統，其總運行成本Ce按式（2）計算。

式中：T為總運行時間；NE為發電機數量；Pij為第i臺發電機在時間間隔ΔTj內產生的功率；Fci為發電機的燃料單價；為發電機特定燃料消耗；WCij為每個運行單位的維護成本；QCij為啟動成本；tij為系數，對于第i臺發電機，若其運行，則tij取值為1，否則為0。

在經典能量管理系統中，由第i臺發電機產生的功率Pij為

式中：E為所有運行的發電機數量；Pel-L,j為在ΔTj內由所有運行的發電機提供的電力負載；Pn,i為第i臺發電機的額定功率。

任何發電機每小時的燃料消耗（FC）與其產生的功率Pi都可以近似地由二階或三階多項式表示：

為了確定系統的最佳工作點，經常使用特定的燃料消耗（SFC）這一參數，它被定義為每小時產生千瓦特功率時的燃料消耗，如式（5）所示。

對于推進系統，其總運行成本Cpr按式（6）計算。

式中：Npr為柴油機數量；Pqj為第q臺柴油機在時間間隔ΔTj內產生的功率；Fcq為第q臺柴油機的燃料成本；SFCq為柴油機特定燃料消耗，與式（5）類似；WCqj和QCqj分別為每個運行單元的維護成本與啟動成本；tqj為系數，對于第q臺柴油機，若其運行，則tqj取值為1，否則為0。

在經典能量管理系統中，第q臺柴油機產生的功率Pqj為

式中：Y為所有運行的柴油機數量；Ppr-L,j為由所有運行的柴油機提供的推進力負載；Pn,q為第q臺柴油機的額定功率。

1.2 約束條件

1.2.1 發電機的相關約束

1）發電機運行約束。

式中，Pmax,i和Pmin,i分別為第i臺發電機發出功率的上、下限。

2）發電機組發出的總功率和電力負載之間的平衡。

3）發電機組爬坡速度約束。

式中，Rci為第i臺發電機的最大爬坡斜率。

4）發電機組的最小連續運行時間約束。

式中，下標on和off分別代表啟動和停機。

5）發電機組最小停機時間約束。

6）預防異常熄火限制（即使最大的發電機離線，發電機也要能夠提供足夠的負載）。

1.2.2 柴油機的相關約束

1）柴油機運行約束。

式中，Pmax,q和Pmin,q分別為第q臺柴油機發出功率的上、下限。

2）柴油機組發出的總功率和推進力負載之間的平衡。

3）柴油機組爬坡速度約束。

式中，Rcq為第q臺柴油機的最大爬坡斜率。

4）柴油機組的最小連續運行時間約束。

5）柴油機組最小停機時間約束。

1.2.3 船舶航速和柴油機功率需求的約束

在船舶推進系統的優化方案中，船舶航速可以適當調整以最大限度地減小FC。負責移動船舶的有效推進力Pe-pr與船舶在特定情況下的總阻力（與船舶的貨物重量和環境溫度等因素有關）和船舶航速V有關，如式（19）所示［9］。

船舶在航行過程中，對航速存在一定的限制：

式中，Vmax,j和Vmin,j分別為相應速度的上、下限。

1.2.4 航行距離的約束

1）船舶初始航行距離和到達目的地時的航行距離約束。

假定船舶在0時刻出發，T時刻到達終點，則

式中：NT為從開始時刻到最后時刻T的離散時間點的數量；Dj為在時刻j的船舶位置；dtotal為航線總行程。

2）船舶到達中間港口時的航行距離約束。

式中：ζ為對應于中間港口的時間間隔集合；dj為在任意時刻j的行駛距離。

根據臨界轉速計算結果，該變頻電動機的機座長度比常規H630-4電動機有所縮短，由2 770 mm縮短到2 650 mm。根據變頻電動機頻繁變速運行的特點，機座壁也比常規電動機厚，鋼板由32 mm加厚到45 mm。

典型的船舶航速、航行距離及其約束曲線如圖1所示。

1.2.5 溫室氣體排放量約束

船舶能效營運指數（Energy Efficiency Opera?tional Indicator，EEOI）體現了單位貨物周轉量（船舶貨物量乘以運輸量）的溫室氣體排放量［4］，該指標側重于對船上操作效率的評估，船舶在航行過程中必須遵循EEOI對氣體排放的約束［10］。

在時間間隔ΔTj內，ηEEOI定義為每單位運輸工作產生的二氧化碳質量的比。

由于溫室氣體排放與FC成正比，所以其質量可以通過將發電機和柴油機消耗的燃料量分別乘以轉換系數ci，cq來計算。因此，船舶在每個時間段ΔTj內的總二氧化碳排放量為

αLF取決于船舶的類型。如果船舶標準乘客人數和車輛數分別為np和nv，實際乘客人數和車輛數分別為n′p和n′v，則αLF為

式中，GT為船舶總噸位。

當船舶處于泊位時，由于船速為0，所以ηEEOI不用式（24）計算，將其修正為［11］

根據各種船舶的設計，常見的環境限制為：

文獻［11］提出了多種方法來減少船舶的二氧化碳排放量，并針對船舶的航行重點采取了降低航速的策略，達到了減少溫室氣體排放量的目的，具有實際參考意義。

1.3 發電調度說明

為了確定發電機和柴油機的使用數量，達到負載功率分配的最優化，需要準確預測船舶負載。這是通過在航行過程中系統地記錄貨物負載和乘客人數來實現的。除柴油機外，工程空間的輔助系統、生活空間和貨艙的空調，特別是游輪的照明等都增加了船舶負載。當給定電力負載的時間順序曲線，即可選擇運行的發電機及其產生的功率。在常規船舶電力系統配置中，通過調整航速來管理負載，減少CO2排放以滿足環境約束。在任何情況下，對于實際負載超出預期的小范圍波動情況，可以由船舶電力系統使用實時最優控制系統通過適當的發電調整［10］和負載優先啟停來管理［12］。

2 差分進化算法

差分進化算法是一種基于種群的智能優化算法，該算法不依賴問題的特征信息，借助于種群個體間的差分信息對個體形成擾動來搜索整個個體空間，并利用貪婪競爭機制進行優化，以尋求問題的最優解。該算法采用實數編碼方式，主要解決連續領域的優化問題［13］。該算法的變異方式可以有效利用群體的分布特性提高算法的搜索能力。

對于優化問題：

2.1 差分進化算法流程

差分進化算法是基于實數編碼，首先要在問題的可行解空間生成隨機初始化種群：xi=(xi,1,xi,2,???,xi,D)，其中i=1,2,???,NP，NP為種群規模。初始種群在參數空間中隨機產生，并應覆蓋整個參數空間。

在進化的每一代中，對每一目標個體進行變異和交叉操作以產生試驗個體，然后對目標個體和試驗個體進行選擇操作，以選擇適應值更優的個體進入下一代。

種群內個體的差分向量經過縮放后，與種群內另外的相異個體相加得到變異向量。

式中：g為代數；r1≠r2≠r3，隨機取自于種群集{i=1,2,???,NP}，這也使得種群的規模NP不能小于4；F為縮放因子，控制差分向量的縮放以避免搜索的停滯，其選擇范圍為 0.5～1［14］。

在變異之后的交叉過程中，通過隨機選擇，使產生的試驗向量至少有一個分量是由變異向量提供。

式中：j=1,2,???,D；jrand為［1，D］內隨機選擇的整數；CR∈(0,1)，為交叉率。

經變異與交叉操作后生成的試驗向量ui,g和目標向量xi,g進行競爭。當ui,g的適應度值較優時，其被選為子代；否則，xi,g為子代。

式中，xi,g+1為下一代的目標向量。

2.2 差分進化算法在本文中的實現步驟

以3.1節的方案2為例，運用差分進化算法對電功率分布進行優化。其實現步驟如下：

步驟1：根據給出的初始數據，在可行解空間隨機生成規模為NP的初始化種群（包含機器運行狀態、速度、發電機和柴油機輸出功率），設置最大迭代次數G，令g=1。

步驟2：對初始化種群中的數值進行修改，使之滿足約束條件（發出功率上下限約束、開/關時間約束、EEOI約束等）。

步驟3：判斷是否滿足終止條件，若是則退出，否則執行下一步。

步驟4：對每一個體xi,g執行步驟5～步驟8，生成g+1代種群。

步驟5：在種群中隨機選擇3個不同的個體，按式（30）進行變異操作，生成變異個體vi,g并按步驟2進行調整。

步驟6：按式（31）進行交叉操作，生成試驗個體ui,g，并按步驟2進行調整。

步驟7：按式（32）進行選擇操作，生成g+1代目標向量xi,g+1。

步驟8：g=g+1，返回到步驟3。

3 仿真與分析

3.1 仿真方案的提出

為了驗證差分進化算法對本問題的有效性，采用文獻［5］中的數據進行對比驗證。該文中客渡船的總噸位為48 750 t，其最高航速為23.5 kn，最大運輸量為1 800名乘客和500輛汽車，EEOI1的最大允許CO2排放值為21 g/（t·kn），EEOI2的最大允許CO2排放值為120 g/（t·h）。使用差分進化算法、粒子群算法和遺傳算法對船舶能量管理系統進行優化，并將其結果與文獻［5］的優化結果進行對比。

仿真運行的船舶配置有3臺發電機和2臺柴油機，每臺柴油機都通過軸連接一個螺旋槳推進裝置。發電機和柴油機的所有必要技術參數見表1。

表1 船舶動力系統模型數據Table 1 Ship power system model data

這里模擬一條總里程為307.744 2 n mile的航線。航線中有3個中間港口，經港路線各部分的乘客、車輛和相應的船舶負載因數如表2所示。該次航行的船舶初始推進力和速度規劃曲線、總負載和電力服務負載預測曲線如圖2所示。

發電機根據運行優先級編號，它們連續的啟動和停止之間的最小允許時間為1 h。每臺工作的柴油機都會以相同的推進負載驅動螺旋槳，柴油機也按照其運行優先順序編號。

本文采取3種不同的運行方案，具體操作如下：

方案1：配有3臺發電機和2臺獨立的推進柴油機，不采用最佳功率調度、推進調整，無EEOI限制，發電機和柴油機采用比例分配方法。

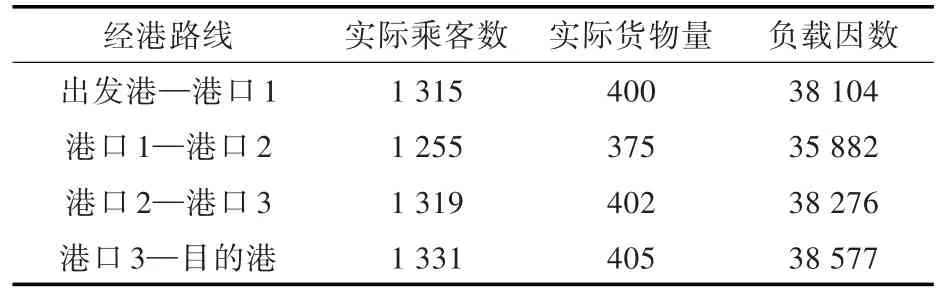
表2 船舶滿載度數據Table 2 Data for ship fullness

方案2：配有3臺發電機和2臺獨立的推進柴油機，采用最佳功率調度，有EEOI限制，不采用推進調整。

方案3：配有3臺發電機和2臺獨立的推進柴油機，采用最佳功率調度、最佳推進調整，有EEOI限制。

3.2 仿真結果與分析

方案1的運行成本為36 960.5 m.u.，方案2的運行成本為36 938.1 m.u.，方案3的運行成本為35 888.3 m.u.。方案2和方案3的運行成本隨進化代數變化的曲線如圖3所示。由圖中可以發現，差分進化算法（DE）與粒子群算法（PSO）和遺傳算法（GA）相比，對本問題有更好的穩定性和收斂性。

在方案2和方案3中提出的能效管理方法用于推導最優電功率分布和最優推進調整，以最大限度地提高船舶電力系統的運行效率，并限制整個行程中的EEOI。所得結果如圖4～圖8所示。假設在所有運行工況下，柴油機1、發電機1和發電機2在t=1時已經運行0.5 h。

由主發電機和推進系統柴油機產生的功率如圖4所示，將其總功率與總需求負載（電力需求加上推進負載需求）進行比較。圖中，EG為發電機，PM為柴油機。

在方案1～方案3中，推進力負載被平均分配給運行的柴油機；方案1中，電力負荷也被平均分配給運行的發電機，在方案2和方案3中，分配方式有變化。發電機1連續運行，發電機2幾乎連續運行（時間段T13～T17除外），而發電機3則僅在高電力負載期（T26～T28）運行。

在方案1和方案2中，船舶航速和推進力未調整，只對電功率分布進行調整，所以其結果僅在電功率分配中不同。船舶總負載在相鄰時間段會發生較大偏差，不能保持相對穩定，運營成本降低量可以忽略不計。

在方案3中，進行電功率和推進力的最佳調整。方案3中的最佳電力調度與方案2的情況非常相似，但柴油機的發出功率有很大改變，船舶總負載在相鄰時間段波動較小，運營成本有很大的降低。

方案1～方案3中船舶每個時間間隔的航行速度如圖5所示。方案3與方案1和方案2相比，隨著推進力得到最佳調整，在海上航行時，船舶航速保持相對穩定；當接近港口時，船舶航速降低，到達港口時速度降為0；當從港口離開時，船舶航速增加。通過這種方式，船速和推進力負載曲線變得相對穩定，不會過于離散，如圖6所示。這使得船舶運行成本的曲線更加接近梯形，操作更經濟，如圖7所示。此外，船舶航速雖然偏離了初始（非優化）的預定值，但不會超過其上限（23.5 kn）。在中間港和目的港，航行距離的限制也是滿足的。

EEOI在所有時間間隔的值如圖8所示。方案3采用推進調整和EEOI限制，能夠保證在其上限（海上航行時為21 g/（t·kn）和泊位時為120 g/（t·h））之下。方案2和方案1相比雖然不能滿足此限制，但方案2的EEOI值略小于方案1。

如前所述，方案1和方案2不包括推進調整，而方案3包含，由圖5～圖8可知，船舶速度變化和預期的一樣，方案1和方案2中的船速保持不變，方案3中觀察到速度的變化，這是因為提供推進力的柴油機功率進行了調整以滿足EEOI限制。

方案1的總運行成本為36 960.5 m.u.，如果采用最優電力調度方案2，則總運行成本降至36 938.1 m.u.（減少0.06%），溫室氣體排放量也略有下降。如果在經典船舶配置中實施推進調整（方案3），則總運行成本降為35 888.3 m.u.（減少2.90%），并且完全滿足EEOI限制。

因此，仿真結果表明，本文提出的優化方法有效降低了運行成本，減少了溫室氣體的排放。

3.3 與已有文獻結果的對比

對比本文方法與采用動態規劃算法的文獻［5］可以發現，在相同的仿真條件下，文獻［5］中的方案2與方案1相比運行成本減少了0.05%，而本文方法則減少了0.06%。同樣，文獻［5］中的方案3與方案1相比運行成本減少了2.02%，而本文方法則減少了2.90%。結果表明，采用差分進化算法對船舶能量管理系統進行優化調度，能夠在滿足各種同等船舶運行約束的條件下，使運行消耗更小，滿足EEOI限制，且船舶航速更平穩。

4 結 語

本文針對船舶電力系統運行成本最小化的需求，提出了一種將差分進化算法應用到船舶動力系統的最優功效管理方法。仿真結果證實了差分進化算法的有效性，盡管同時考慮經濟性和環保性會使問題變得復雜，但還是能夠在滿足船舶電力系統的技術和運營限制（包括生產和消耗平衡、總航行距離、溫室氣體排放等限制）的同時，實現運行成本最小化。所提出的算法可用于評估任何船型，它是完全參數化的，不依賴于船舶柴油機或發電機的任何特定特征，因為它的主要輸入是發動機和發電機的燃油消耗率曲線。