百度地圖坐標解密方法精度分析

楊丁亮，劉志平，仲崇武

(1. 中國礦業大學環境與測繪學院，江蘇 徐州 221116； 2. 兗州煤業股份有限公司南屯煤礦，山東 鄒城 273515)

百度地圖是一款具有導航、定位和量算等功能的可視化電子地圖[1]。與此產生的LBS服務有路徑導航[2]、本地搜索[3]和地址解析等。文獻[4]和文獻[5]利用百度地圖量算工具實現了野外測距和圖上測量農用地面積。文獻[6]和文獻[7]將有軌電車和采棉機路徑在百度地圖上可視化，實現了交通的實時監控。文獻[8]和文獻[9]在室內提取百度地圖興趣點坐標建立地理國情普查數據庫，提高了工作效率。

文獻[4]和文獻[5]采用百度地圖坐標雖然得到距離和面積，但與實際值有較大誤差。文獻[6]和文獻[7]涉及WGS-84坐標轉換到百度地圖坐標問題，通過百度地圖提供的坐標轉換API解決。而文獻[8]和文獻[9]涉及百度坐標轉換到WGS-84坐標問題，其轉換方法存在精度較低的問題。鑒此，本文選取烏魯木齊、拉薩、蘭州、北京、上海和三沙6座城市，利用等量偏移法、BP神經網絡[12]和格網法[10]對百度地圖坐標解密到WGS-84坐標，比較分析3種解密方法的精度及適用范圍，最后通過距離和面積計算對本文方法進行實際應用驗證。

1 百度坐標獲取

百度地圖坐標(BD09)是由WGS-84坐標經非線性變換而得，并且不同區域坐標加密變換不同。為使WGS-84坐標與BD09坐標點對應，百度地圖提供了坐標轉換API，但該API只允許將WGS-84坐標轉換為百度坐標，不能將BD09坐標轉換成WGS-84坐標。本文利用坐標轉換API開發了百度坐標獲取程序。該程序涉及的轉換代碼如下：

converter=newCoordinateConverter();

converter.from(CoordType.GPS);

converter.coord(sourceLatLng)；

LatLng desLatLng=converter.convert();

2 百度坐標解密方法

2.1 等量偏移法及其改進

為了保持地圖上各種地物相對位置關系，近距離點的坐標經過百度坐標變換后的偏移量是接近的。假定LWGS和BWGS是WGS-84坐標，經百度坐標API轉換后得到BD09坐標LBD1和BBD1，對LBD1和BBD1再次進行百度坐標API轉換得到LBD2和BBD2。根據近距離點偏移量近似原則，可近似表示為

(1)

通過變換得到

(2)

由式(1)和式(2)可知，等量偏移法基本思想是差分思想[13]，且式(2)本質上屬于一階差分方法。若記n階差分算子為[α1,α2,…,αn]，本文在此基礎上推導出n階差分的等量偏差法通用表達式

(3)

式中，LBDi、BBDi由LBDi-1、BBDi-1經百度坐標API依次轉換得到。

文中選擇二階差分方法，作為與一階差分的對比方法，二階差分算子為[α1,α2,α3]=[1,-2,1]，可得其表達式為

(4)

2.2 BP神經網絡

BP神經網絡是非線性不確定性數學模型，使用誤差反向傳播算法，并以均方誤差最小化為目標不斷修改網絡的權值和閾值，最終能高精度地擬合數據[12]。該模型可分為輸入層、中間層和輸出層，其中輸入和輸出都只有一層，中間層可有一層或多層。本文選用Matlab軟件建立BP神經網絡，使用雙隱層結構，每一層包含10個神經元，設定訓練誤差目標為10-8，最大迭代次數為4000，學習速率為0.05。其基本步驟如下：

(1) 獲取訓練數據。根據研究區域的經緯度范圍利用百度API隨機生成WGS-84坐標和對應的BD09坐標。

(2) 建立及訓練BP網絡。將步驟(1)中BD09坐標作為訓練輸入數據、WGS-84坐標作為訓練輸出數據訓練BP網絡，從而擬合BD09變換WGS-84的轉換函數。

(3) 預測待定點的坐標。根據步驟(2)中轉換函數，預測新的BD09點對應的WGS-84坐標。

2.3 格網法

將研究區域劃分到若干固定間隔的網格內，計算每個網格角點的WGS-84坐標與百度坐標的差值，根據最鄰近原則，選取最近格網角點的差值作為坐標偏移修正值。設采用WGS-84點坐標為LWGS和BWGS，對應BD09的坐標為LBD和BBD，則經緯度偏移量分別為ΔL、ΔB，見式(5)。如圖1中落在格網內的P1和P2點，按最鄰近原則，P1點坐標修正值為ΔL1、ΔB1，P2點坐標修正值為ΔL4、ΔB4，但坐標偏移量會隨坐標點的改變而變化。

(5)

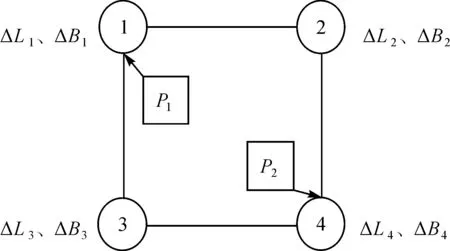
圖1 格網法

3 試驗結果與分析

3.1 不同坐標解密方法比較

在烏魯木齊、拉薩、蘭州、北京、上海和三沙6個城市的中心分別建立0.1°方格的研究區域，并利用百度坐標API分別隨機生成1000對樣本數據。其中，WGS-84坐標數據作為參考值，BD09坐標數據作為輸入值。為驗證上述方法的百度坐標解密精度，設計了如下4種方案：

方案1：等量偏移一階差分法。將樣本BD09坐標利用百度坐標API再次轉換，根據式(2)預測對應的WGS-84坐標。

方案2：等量偏移二階差分法。將樣本BD09坐標利用百度坐標API連續兩次轉換，根據式(4)預測對應的WGS-84坐標。

方案3：BP神經網絡法。根據研究區域利用百度坐標API再次隨機生成1000組WGS-84′坐標和對應的BD09′坐標，以BD09′坐標作輸入訓練，WGS-84′坐標作輸出訓練，擬合BD09到WGS-84的轉換函數，從而預測對應的WGS-84坐標。

方案4：格網法。將各研究區域等分為100行×100列的格網，利用百度坐標API計算每個格網角點坐標，根據式(5)及最鄰近點原則，預測對應的WGS-84坐標。

根據上述4種方案，以烏魯木齊和三沙為例，繪制了WGS-84坐標預測值與參考值的差值分布(如圖2和圖3所示)和點位誤差分布(如圖4和圖5所示)。圖4和圖5的RMS、mean分別代表點位誤差的均方根值和平均值。

圖2 烏魯木齊4種方案經緯度差分布

圖3 三沙4種方案經緯度差分布

從圖2和圖3可得，4種方案WGS-84坐標預測值與參考值的經緯度差值均達到10-4量級，其中方案1和方案2甚至達到10-5量級。此外，方案1和方案2呈現高度集并匯聚成圓點，方案3沿(0,0)朝縱軸或橫軸方向呈矩形發散，方案4沿(0,0)向四周呈正方形發散。

圖4 烏魯木齊4種方案點位誤差分布

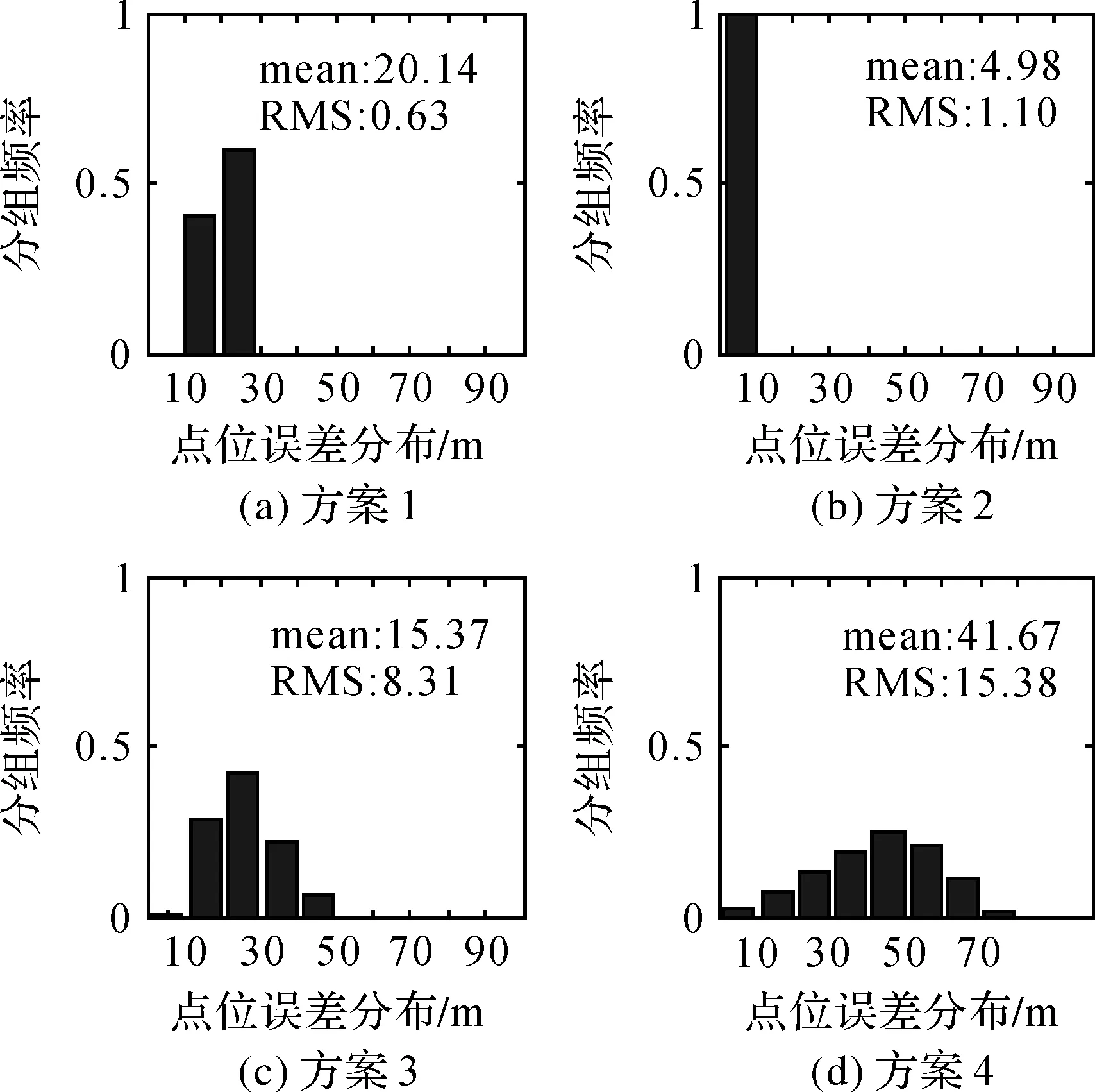
圖5 三沙4種方案點位誤差分布

從圖4和圖5可得，方案1和方案2點位誤差分布以單條狀為主，方案3和方案4分別呈現偏態分布和正態分布。方案1、方案2、方案3和方案4的點位誤差分別集中在10～20 m、0～10 m、10～30 m和30～60 m。綜合RMS值和mean值大小，以及點位誤差分布形態，百度坐標解密方法精度由高到低依次是方案2>方案1>方案3>方案4。其他城市的解密精度分析均可得出相同結論，限于篇幅不再論述，見表1。

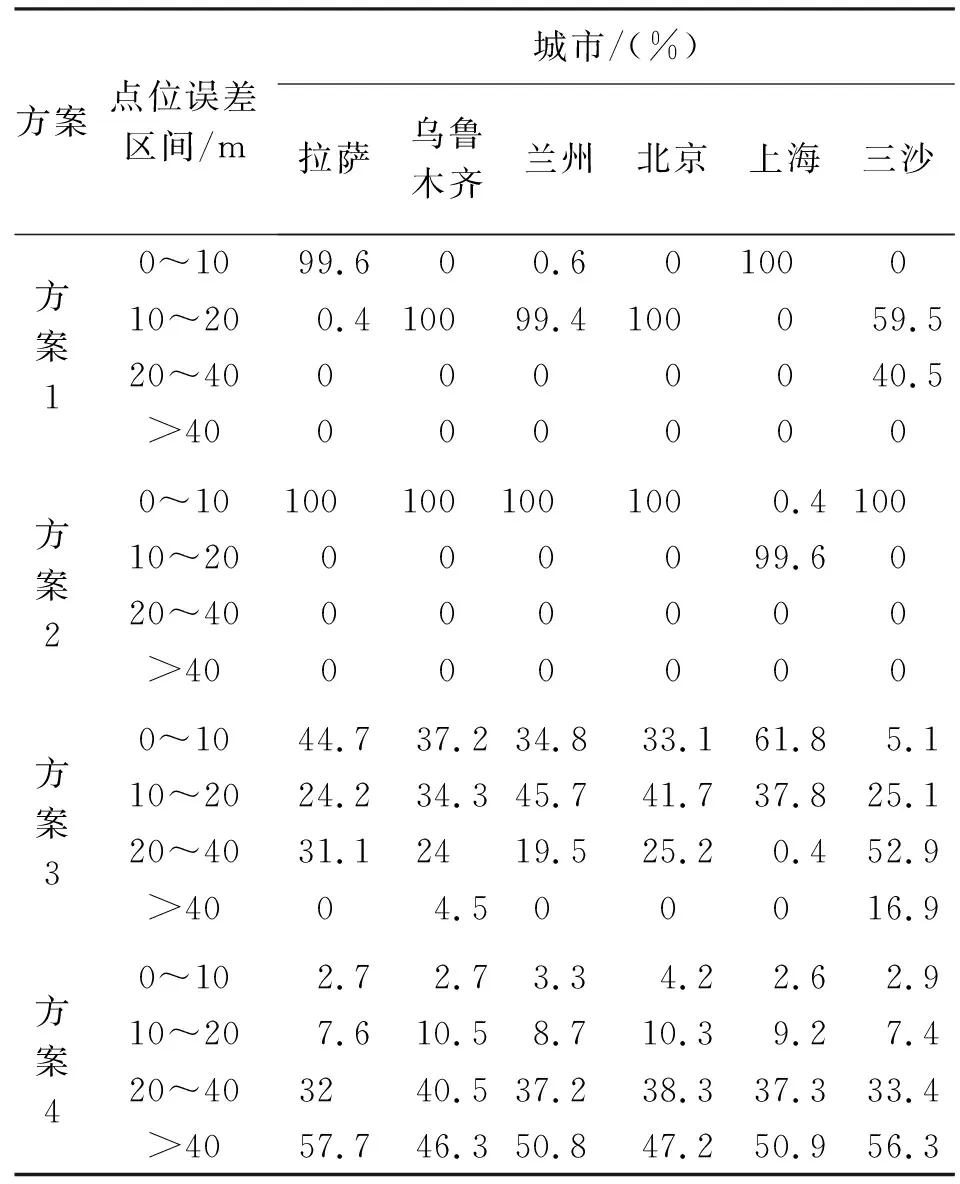
表1 各城市不同解密方案的點位誤差占比

從表1可得，方案1最大的點位誤差區間是[20 m,40 m)分布在三沙，集中分布在[10 m,20 m)。

方案2最大的點位誤差區間是[10 m,20 m)分布在上海，集中分布在[0,10 m)。方案3點位誤差區間分布不均勻，點位誤差集中分布在10～40 m。方案4點位誤差分布離散，約有50%的點位誤差大于40 m。上述結果表明，方案1和方案2在地理位置上具有較強的適用性及較高的坐標解密精度。

3.2 坐標解密應用效果分析

選擇兩點歐氏距離和以兩點為對角線構成的矩形面積作為百度坐標解密的實際應用驗證。在谷歌地球選取3組WGS-84坐標點，經高斯投影[14]計算真實距離與面積。方案1和方案2的距離和面積通過坐標解密后投影成高斯平面直角坐標計算得到；百度地圖量距和面積通過百度地圖量算工具得到。表2羅列了方案1、方案2和百度地圖獲取的距離、面積與真實距離和面積的相對誤差。

從表2可得，在獲取實際距離和面積時，百度地圖工具量測的方法相對誤差最大，方案2相對誤差最小。隨著距離和面積的增加，3種方案與真實值的相對誤差均呈現遞減趨勢，且在距離計算中3種方案的精度接近，但在面積計算中方案2精度仍有優勢。故在百度地圖上直接量取的距離和面積代替真實值是不嚴謹的，而經方案1和方案2解密后的距離和面積更加接近真實值。筆者建議在數百千米內計算面積，選用方案2；在1～10 km內的距離，選用方案2；其余情況，可以選用方案1或方案2。

表2 不同方案的幾何測量與真實值對比

4 結 語

本文提出了等量偏移法、格網法和BP神經網絡3種百度坐標解密方法，并引申出二階等量偏移法公式。選用拉薩、烏魯木齊、蘭州、北京、上海、三沙6座城市作為研究區域，采用上述方法比較了解密精度。結果表明,等量偏移二階差分法、一階差分法、BP神經網絡法和網格法誤差水平分別可至10、20、50和100 m。同時利用百度地圖提供的距離和面積量算工具、等量偏移一階差分法、二階差分法進行了實際測距、面積的應用驗證。值得注意的是，等量偏移法的解密精度不隨研究區域發生改變。BP神經網絡會因訓練樣本的分布是否均勻而使坐標解密精度發生變化。而格網法坐標解密精度只與格網間距相關，間距越小解密精度越高，但坐標偏移修正數據庫將呈數量級增長。