一種改進的KBM法求解非線性振動方程

王磊佳, 張鵠志, 胡 輝, 祝明橋

(1.湖南科技大學 土木工程學院，湖南 湘潭 411201;2.湖南科技大學 結構抗風與振動控制湖南省重點實驗室，湖南 湘潭 411201)

非線性振動理論的研究對象主要包括不同參數、初始條件對系統解的影響，不同振動系統的振動規律，分析周期解的形式，研究解的穩定性等方面的問題[1-4]。近似解析法作為研究非線性振動解的主要方法之一[5-6]，主要通過應用數值計算方法的思想構建近似解，且研究對象僅限于弱非線性振動系統，其中具有代表性的方法有：Lindstedt-Poincare(L-P)法[7]、多尺度法[8]、平均法[9]、KBM法[10]。

關于非線性振動系統的求解，當前國內外學者進行了不少研究，如：Cheung等[11]提出了一種改進的L-P方法求解強非線性系統；楊志安等[12]將理論與實踐結合總結出了一種對多尺度法的改進理論；陳立群等[13]將平均法應用到了求解多自由度的非線性振動系統；Lim等[14]通過改進Mickens迭代方法求解非線性振動方程拓寬了εA2的取值區間；He[15]拓展了攝動理論將其應用在求解強非線性振動系統領域；Nayfeh[16]求解出了Dffing方程固有頻率的精確解。

在已有的方法中，多尺度法和L-P法都是建立在攝動法[17]的基礎上，攝動法不僅可以計算周期振動，而且適用于耗散系統的衰減振動；不僅可以計算穩態響應，而且可以求出瞬態過程。平均法作為一種新的計算方法，它與攝動法相比，可以避免攝動法的許多繁瑣的中間過程，快速獲得結果，但因為計算中精度僅能達到與ε同階的一次近似解，從而難以滿足高精度定量計算的要求。KBM法是在平均法與攝動法的基礎上提出來的，吸取它們各自的優點，并在求解含有小參數ε的弱非線性振動系統方面得到了廣泛的應用，但隨著ε或振幅a的增大，KBM法也難以滿足精度要求，因而需要展開進一步的研究。

1 改進的KBM法

弱非線性自治方程為

(1)

式中:ε為一個小參數。當ε≠0時，由于式(1)右邊攝動項的存在，使得非線性方程的解中除頻率為ω0的主諧波外，還含有微小的高次諧波，且振幅與頻率均與ε相關，并緩慢變化，因此，運用常數變易法可以構造出該非線性自治方程的一個級數解

(2)

式中:xi(a,ψ)(i=1,2,…)為ψ的以2π為周期的函數，且a和ψ均是隨時間t緩慢變化的函數，可由以下微分方程確定

(3)

(4)

式(3)和式(4)為經典KBM法的基本方程，當ε無限小時，由于該方法的二次近似解精度較高，而被廣泛的應于求解非線性自治方程。隨著ε的增大，該方法解的精度也會隨之下降，工程中通過增加求解ε的冪次可以提高精度，但是當ε增大到一定程度時仍會出現求解精度過低甚至無法求解的問題。

為了解決這個問題，本文將式(4)的等式兩邊同時平方，得到：

(5)

式中頻率分量ωi(a)(i=1,2,3…)未知。

經典KBM法在預設解的形式時存在某種任意性，再通過解的周期性要求以消除該任意性。這種方法在求解非線性振動問題中是行之有效的，因而可求得周期解或非周期解。經典KBM法假定頻率ω與ε相關，但忽視兩者的具體關系，式(4)最終在攝動過程中逐步得以確定。據此可知，本文中對式(5)的假定同樣能滿足這一系列要求。

為了消除長期項并保證Ai和ωi的唯一性，則函數xi(a,ψ)必定不是關于sinψ和cosψ的諧調方程，由式(3)和式(5)得

(6)

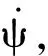
(7)

式(7)兩邊再次對時間t求導，整理得：

(8)

將式(2)和式(8)代入式(1)，左邊整理得：

(9)

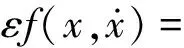
(10)

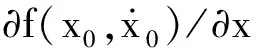
式(9)和式(10)恒等，則兩式ε的同次冪系數必相等。因為xi是關于時間t的周期函數，所以可以確定頻率分量ωi(i=1,2,…)。為消除長期項，令式(9)和式(10)中sinψ和cosψ項的系數為零。在實際計算中只需取級數解的前幾項為近似解就可以達到較高的精度，本文算例中只取到ε2項，整理得：

引入邊界條件，代入式(11)和式(12)即可求解方程的近似解和頻率解。

由以上的推導過程不難發現，改進后的KBM法不僅求解過程簡單，利于驗算，而且適用于電算。

2 算 例

Duffing方程系統是一種典型的非線性系統，工程實際中的許多非線性振動問題的數學模型都可以轉化為該方程來研究，Duffing方程一般表示為

(13)

邊界條件為

(14)

由初始條件可知

x=x0+εx1+ε2x2+…+εixi,

(15)

ω為非線性振動的固有頻率，xi,ωi待確定。

(16)

將式(15)和式(16)代入式(13)化簡得

(ω2-εω1-ε2ω2-…)(x0+εx1+ε2x2+…)+

ε(x0+εx1+ε2x2+…)3=0

(17)

應用和的立方公式，將式(17)整理成關于ε的冪函數

(18)

式(18)中ε≠0，而方程要衡等于零,則必有ε的系數分別等于零。整理得

(19)

(20)

(21)

由式(14)的初始條件可分別求得

x0=acosψ

(22)

(23)

(24)

由式(22)、式(23)和式(24)求得式(15)前兩項的近似解為

(25)

(26)

其中ψ=ωt+ψ0,由Meirovitch[18]的討論方法可以確定出a和ψ0與初始條件間的關系，令ψ0=0代入式(15)、式(25)得

(27)

a關于ε的冪級數為

a=a0+εa1+ε2a2+…

(28)

將式(28)代入式(27)得

(29)

將式(29)表示成ε的冪次函數，并忽略高于ε2的項。由初始條件ε≠0,可以推得ε前的系數等于0，由此理論可以得到

(30)

(31)

求得

(32)

將上式代入式(28)整理得

(33)

將式(33)代入式(26)和式(25)，并將其整理成關于ε的冪函數得

(34)

(35)

式(35)整理得

(36)

經典KBM法關于Dffing方程的二次近似解為

(37)

(38)

3 結果與討論

3.1 頻率ω的近似解分析

本節以求解Duffing方程為例，將本文改進后的KBM法與以下幾種常見方法進行對比。

(39)

(40)

(41)

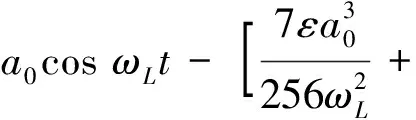
(42)

Duffing方程的精確解為

(43)

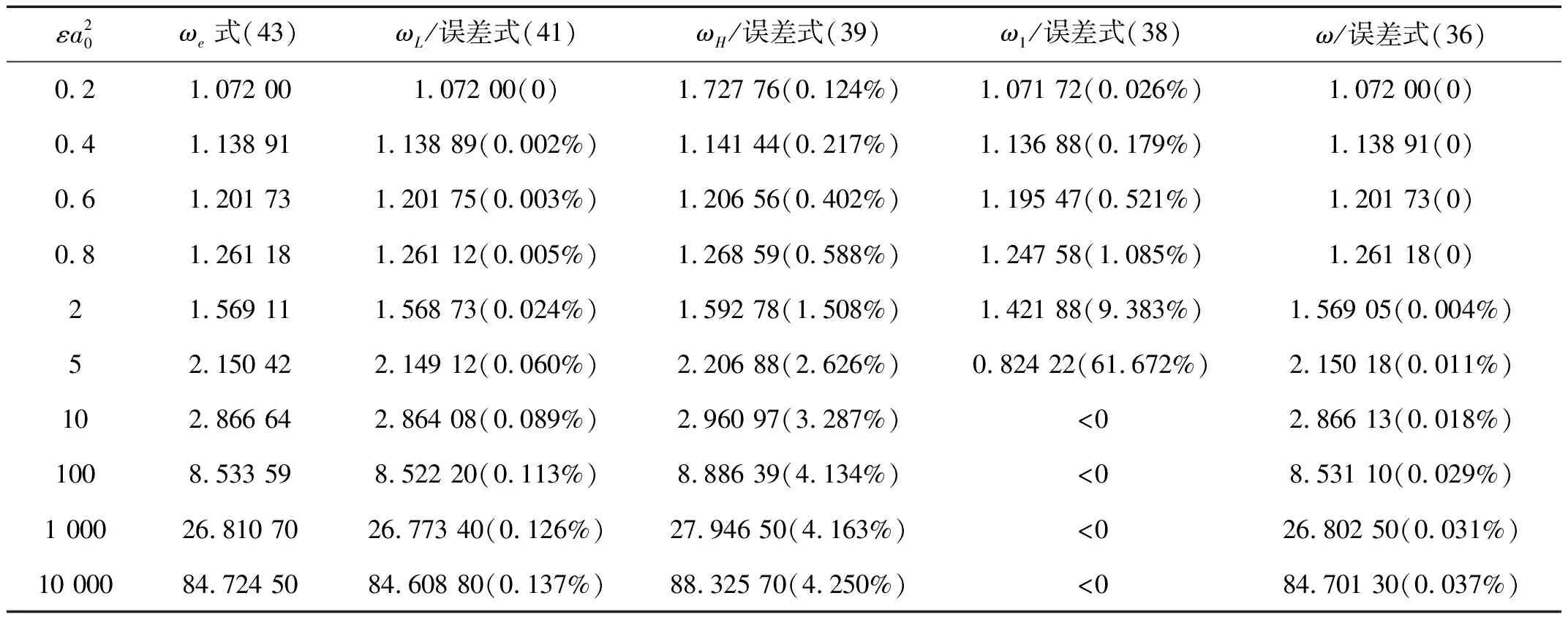
表1 幾種不同方法求得的ω近似解的比較

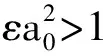
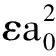
3.2 解析解x(t)的對比分析

為對比實參數ε和振幅a分別取不同值時經典KBM法、He法、Lim法與本文改進后的KBM法求解Duffing方程二次近似解的精度，本節將四階龍格-庫塔法[19]求得的函數在一個周期內的數值解與上述四種方法求解的結果進行對比，如圖1所示。其中ω0=1。

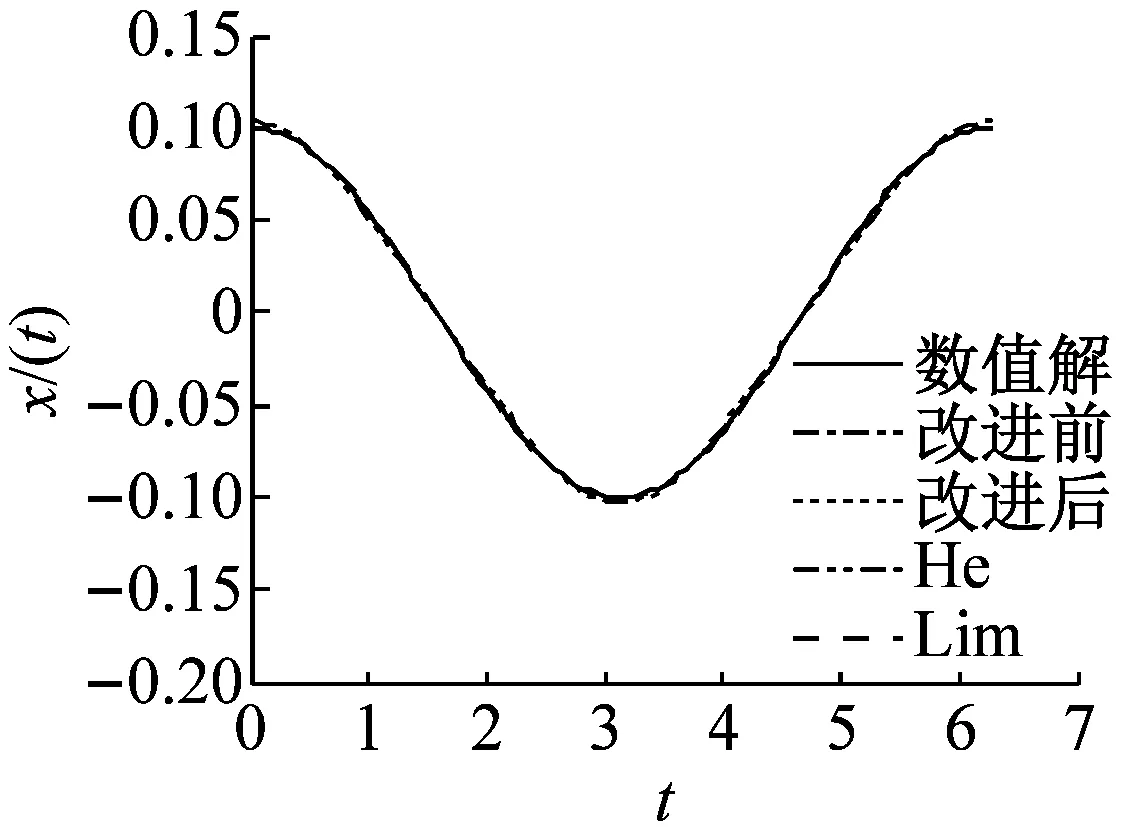
(a) a=0.1,ε=1

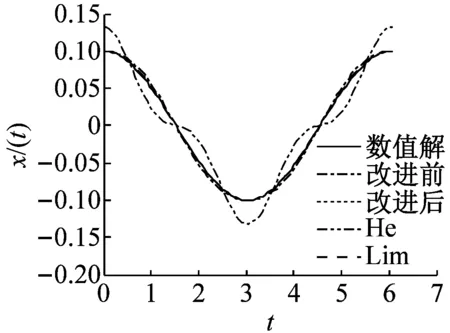
(b) a=0.1,ε=10

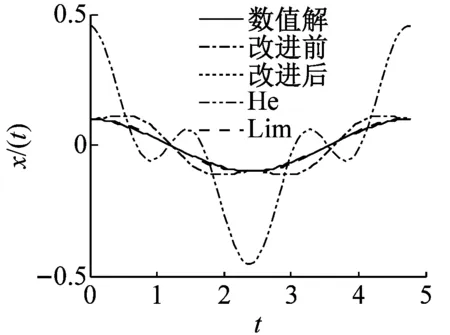
(c) a=0.1,ε=100

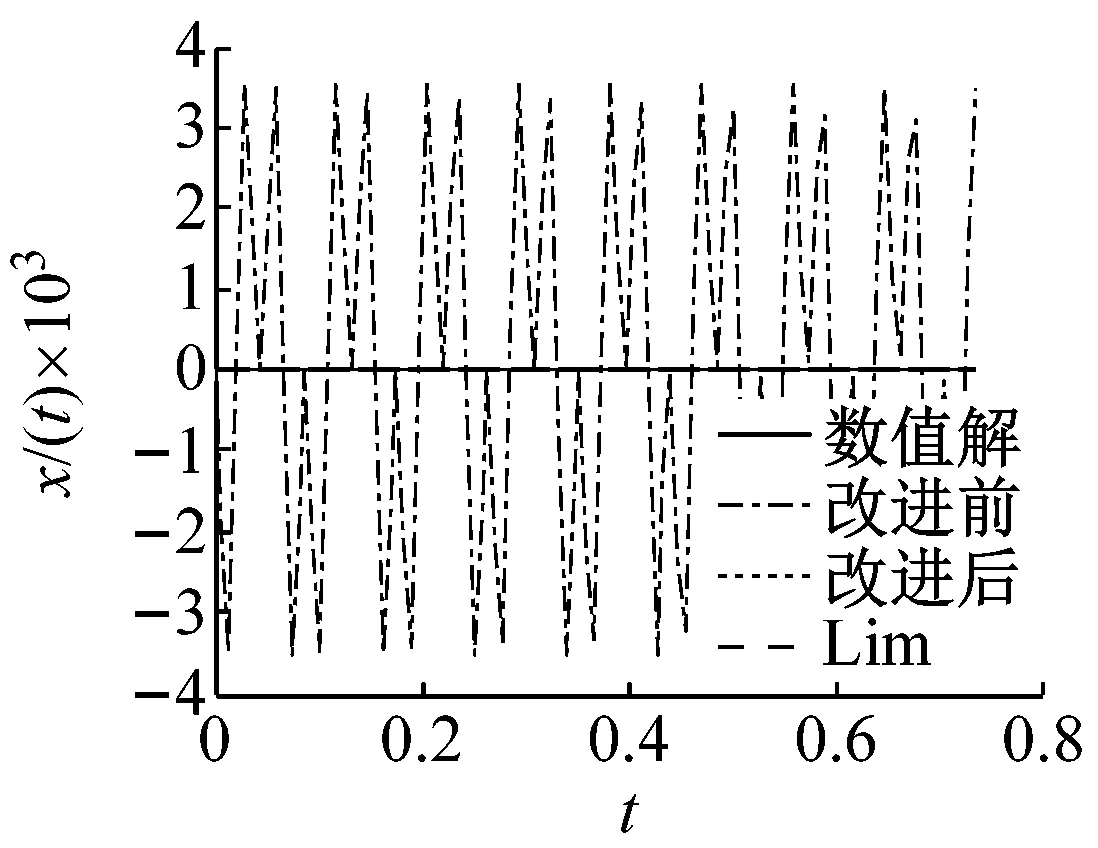
(d) a=10,ε=1

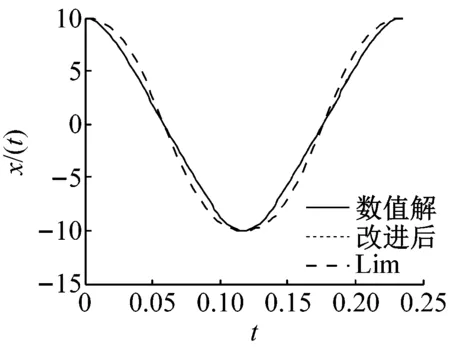
(e) a=10,ε=10

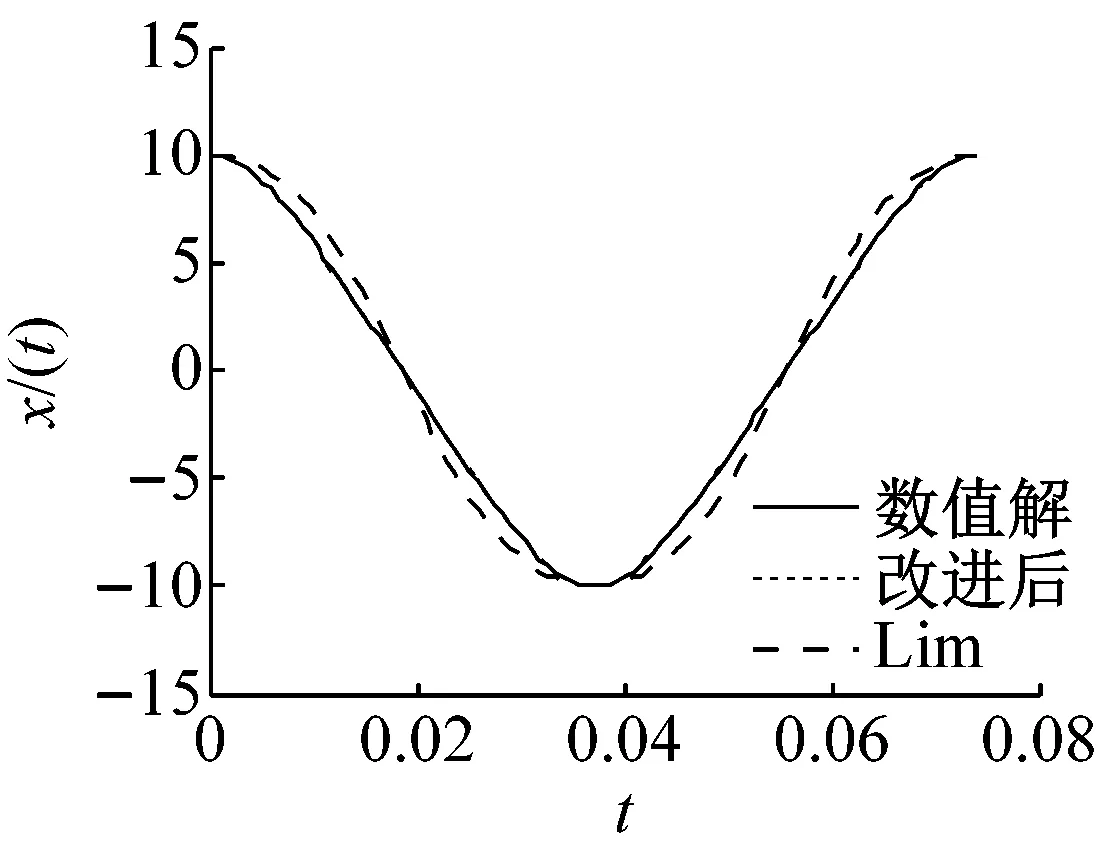
(f) a=10,ε=100

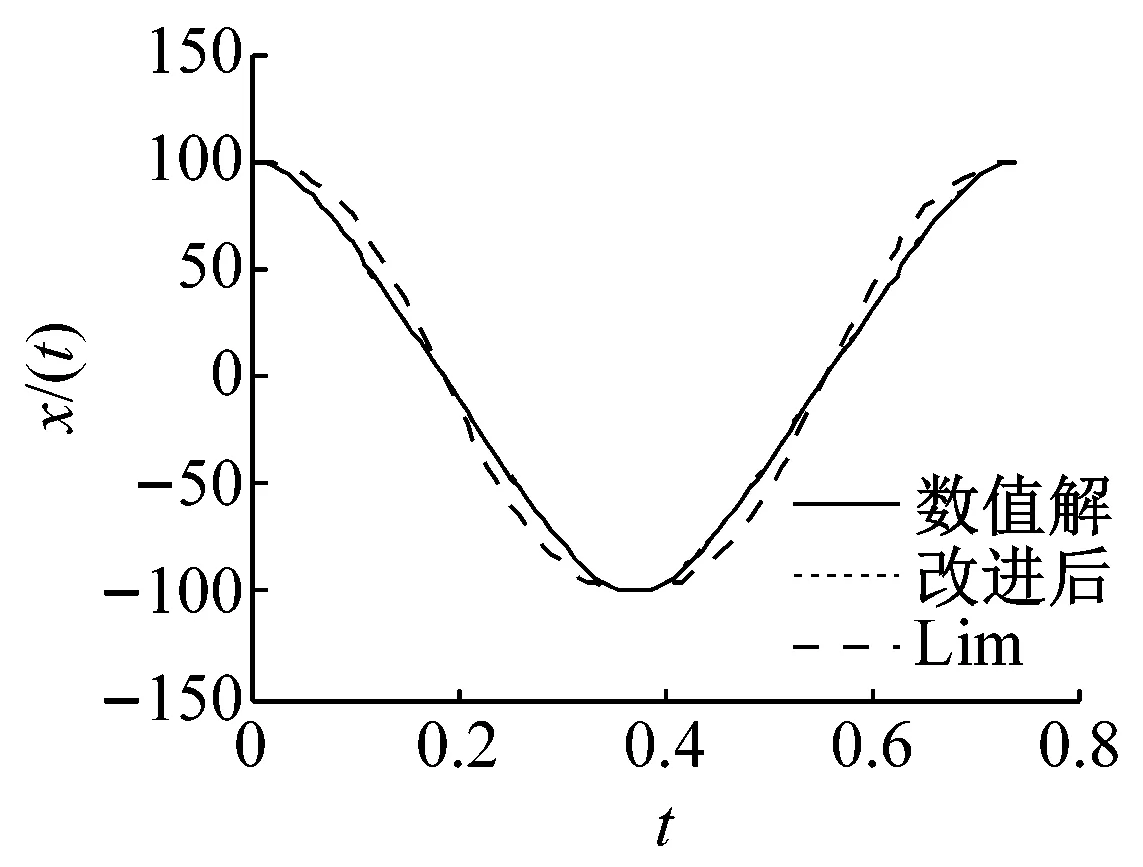
(g) a=100,ε=1

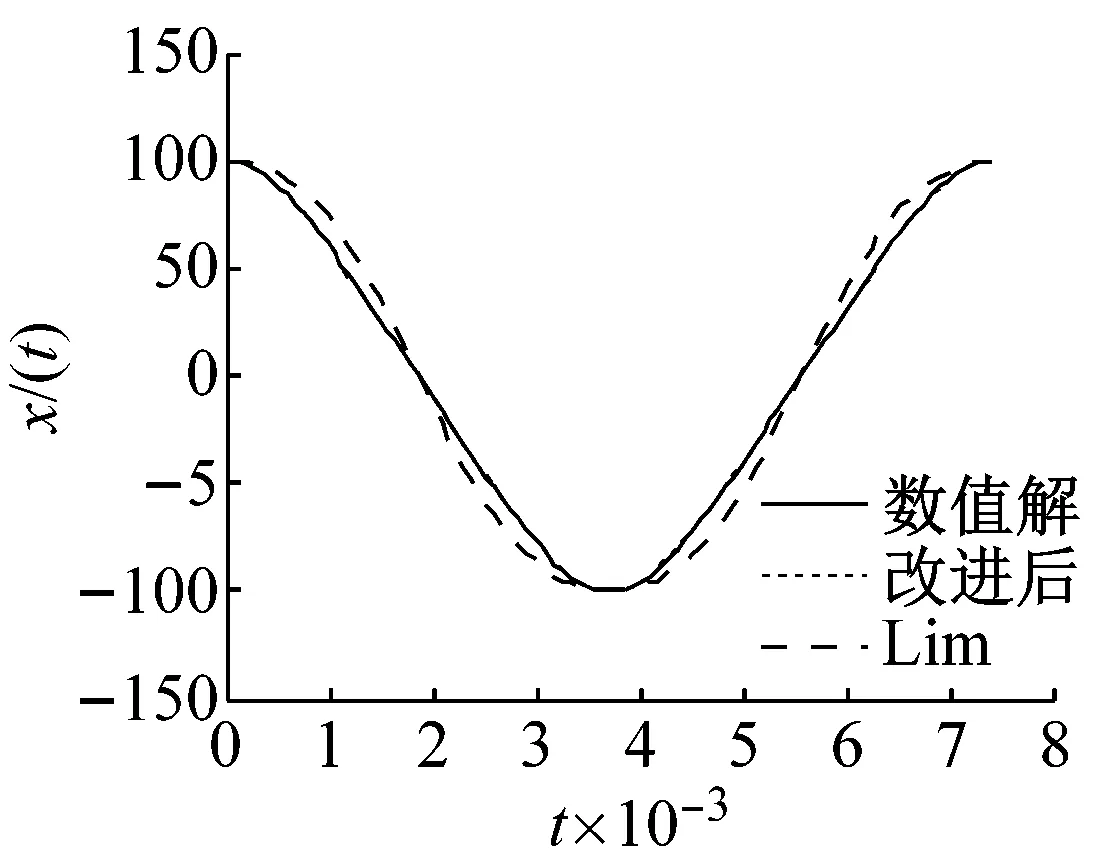
(h) a=100,ε=100

(i) a=100,ε=10 000

圖1中(a)、(b)和(c)對比發現，當振幅a=0.1時，四種方法求得的近似解在ε=1時都非常接近數值解；當ε=10時，He法求得的近似解因誤差較大而不能在實際工程中應用；當ε=100時，改進后的KBM法和Lim法的二次近似解依然非常接近數值解，但經典KBM法的二次近似解開始偏離數值解。由此表明，當a較小且ε較大時，改進后的KBM法和Lim法的近似解都具有較高的精度。

圖1中(d)、(e)和(f)對比可以看出，當振幅a=10，ε=1時，經典KBM法的近似解已經完全偏離數值解從而不能應用于求解非線性振動方程；同時隨著ε取值的增大，Lim法的近似解也開始偏離數值解；由(g)、(h)和(i)對比可知，雖然Lim法的近似解已經偏離數值解，但偏離的范圍沒有隨著ε的增加，而明顯增大，也正是因為如此，Lim法自提出以來被廣泛的應用于求解此類非線性振動方程的周期解，但Lim法的迭代過程繁瑣，且需要根據解的精度要求調整迭代次數；改進后KBM法與Lim法相比，不僅求解簡單，且解的精度高于Lim法。

圖1中(a)、(d)和(g)，(b)、(e)和(h)，(c)、(f)和(i)對比發現，當ε一定時，隨著a值的增大，Lim法的近似與改進后的KBM法的近似解相比，Lim法在數值解上下擺動受振幅取值影響較大，改進后的KBM法的近似解一直非常接近數值解。由此證明，在求解Duffing方程中，改進后的KBM法不受振幅a取值的影響。

4 結 論

(1) 本文通過對經典KBM法中的頻率方程進行平方改進，提出了一種改進的KBM法，該方法的求解范圍不再受小參數的限制。

(2) 基于改進后的KBM法求解Duffing方程時，可將ω0用ω的相關方程表示，以達到簡化計算的目的，且此方法可推廣于求解其它類型的非線性振動方程。

(3) 較之當前已有的幾種主流方法，改進后的KBM法在求解非線性自治方程時均可得到較高精度的二次近似解和頻率解。