循環載荷下考慮累積塑性破壞的船體缺口板CTOD理論及數值模擬研究

董 琴 ， 楊 平 ， 余志鋒

（1.高性能船舶技術教育部重點實驗室（武漢理工大學），武漢430063；2.武漢理工大學 交通學院，武漢 430063）

0 引 言

近年來，隨著船舶主尺度的不斷加大，為減輕結構重量而采用的高強度鋼越來越多，船舶結構變得越來越“軟”，船舶結構的應力及變形也越來越大，當應力達到材料的屈服強度時，裂紋尖端附近區域就會產生塑性應變。當塑性應變隨著循環次數的增加而累積到一定程度時，必然會加速結構的斷裂失效。在彈塑性斷裂力學中，裂紋尖端張開位移（CTOD）和J積分是描述韌性結構材料裂紋擴展的主要參數（Hutchinson，1982）[1]；但由于J積分不適應于卸載狀態，故而很少應用于循環載荷下的結構斷裂評估。因而，研究建立循環載荷下基于累積塑性應變的裂紋尖端張開位移（CTOD）評估方法具有十分重要的意義。

裂紋尖端張開位移（CTOD）指的是裂紋尖端處受載荷后兩個表面所張開的相對位移，其值的大小反映出材料抵抗疲勞裂紋的產生和擴展的能力，故CTOD可以作為評價材料抗脆性斷裂特性的主要參量。先前，一些僅適用于線彈性狀態的基于應力強度因子K的CTOD計算模型相繼被提出（Dugdale，1960；Cottrell，1975；Yaowu，1998）[2-4]。Dugdale模型直接建立了外載荷與裂紋參數的對應關系而得到廣泛的研究和應用。姜翠香[5]基于Dugdale模型對船舶加筋板CTOD進行了分析，找出了外載荷、剛度比等因素對其的影響規律。 有限元法(Potirniche et al，2003；Wu，2009；Chen，2011，2015)是目前研究彈塑性斷裂問題的有效途徑之一，因而被廣泛應用于各種斷裂評估中；它是通過對裂紋尖端應力場、位移場的有限元計算，研究裂紋尖端張口位移CTOD及相關參數。Potirniche等人[6]采用有限元方法計算了穩定的微觀結構小裂紋其裂紋尖端的塑性區尺寸及CTOD值，將單晶體塑性理論的二維小應變本構關系引入ANSYS有限元軟件中，得到了具有較高精度的CTOD值。Wu等人[7]提出了基于CTOD的數值結果估算試件斷裂韌性的有效方法，方法中以軸向切口拉伸試樣為研究對象，采用彈塑性有限元方法計算試樣的CTOD值等。我國學者陳景杰[8-9]基于裂紋最大張口位移CMOD對CTOD進行了數值分析，消除了外載荷、模型尺寸、材料特性及裂紋長度等因素對CTOD的影響，簡化了有限元計算模型。另外，也有學者基于裂紋尖端局部應變相繼對CTOD進行了研究，并提出了僅適用于低應變、靜載荷條件下的CTOD計算模型（Schwalbe，1994；Linkens et al，2000；Jayadevan et al，2004）[10-12]。 日本學者 Shimanuki Hiroshi[13]基于局部應力與線彈性斷裂力學的關系，提出了評估局部應力的新方法，并以焊趾處含有裂紋的十字形接頭為研究對象，采用二維有限元方法，討論了局部應變與CTOD間的對應關系，實現了基于局部應變確定CTOD的思想；對于含裂紋結構在復雜載荷狀況下應用這些計算模型引起了廣泛討論，目前，很多學者在復雜載荷下對CTOD進行了相應研究，并得出了相應結論。和提出CTOD計算模型一樣，Bjerke等（2011）[14]，Yi等（2014）[15]和 Ostby（2005）[16]對發生大范圍塑性變形的含裂紋管道結構進行了數值計算，并提出了一種簡單的基于塑性應變的CTOD評估方法。Zhang（2014）[17]討論了海洋管道結構承受大范圍塑性應變時基于應變的CTOD評估模型，考慮了裂紋尺寸、材料硬化指數以及外載荷對CTOD的影響。

從以上分析可知，目前對CTOD的研究要么局限于線彈性狀態，要么僅在靜載荷條件下結合塑性應變理論對CTOD進行有限元分析；對于承受低周循環載荷下的含裂紋船體板的斷裂評估目前很少有觸及。本文結合船舶結構在航行過程中承受的低循環高應力外載荷條件，以含中心穿透裂紋船體板為研究對象，建立一種基于裂紋尖端局部區域累積塑性應變的CTOD計算模型；并對循環載荷的應力比、應力幅的影響進行數值分析。通過本文的分析為評估船舶構件在實際承載狀態下的斷裂失效提供參考。

1 理論分析

式中：σy為材料屈服極限，dn取決于材料的硬化行為。對于冪硬化材料，其裂紋尖端的應力應變場是Hutchinson，Rice 和 Rosengren（HRR）[19-20]奇異場。 在此種情況下，dn是 Ramberg-Osgood 硬化指數 n 的

對于理想彈塑性材料，Shih[18]對承受單向載荷作用下的含中心穿透裂紋的無限大板進行研究并給出了J積分和無限大板裂紋尖端張口位移（CTOD）之間的計算公式：函數并且由Shih[21]在平面應力和平面應變下的數值做了系列表格。對于平面應力的情況，dn由以下三次多項式給定：

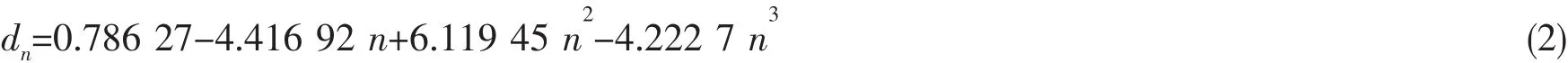
循環載荷下，對于表現Masing行為的材料，循環J積分ΔJ有可靠的數學基礎。公式（1）中所有的參量可由對應的循環參量表示，由Kumar等[22]和Heitmann等[23]的研究可知，循環J積分ΔJ可近似由彈性（小范圍屈服）和塑性部分疊加而成。假設在平面應力的情況下，對于I型裂紋，我們可得到：

式中：n′為循環硬化指數，σcy為循環屈服強度，E為彈性模量，a為裂紋半長，Δσ為應力幅值，Δεpl為塑性應變幅值。在循環J積分ΔJ彈性部分，采用有效應力幅值考慮裂紋閉合效應，Δσeff=σmax-σop，σmax和σop分別表示為最大應力和裂紋張口應力。裂紋張口應力σop可通過經驗公式估算或者由數值分析結果獲取。本文中，裂紋張口應力通過Newman[24]得到，在低周疲勞作用下較小的裂紋張口應力對應較大的最大應力：

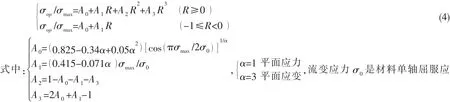
力和單軸極限拉伸應力的平均值。

由文獻[25]Chaboche模型中塑性應變與累積塑性應變間關系微分可得：

式中：Δpn+1是第n+1次載荷循環后在裂紋尖端產生的等效塑性應變增量，通過Newton-Raphson迭代即可求得；故第n+1次循環后對應的累積塑性應變增量Δεn+1可得；依次更新相應參量，可求得每次對應循環下的塑性應變增量。

在循環載荷下，在第n+1次循環狀態下裂紋尖端塑性應力應變關系可用Ramberg-Osgood表達為[26-27]：

將（6）式代入文獻[25]求解Δpn+1的Newton-Raphson迭代公式中，即可求得第n+1次循環后裂紋尖端塑性應變增量Δpn+1，然后利用公式（5）即可獲得第n+1次循環后裂紋尖端累積塑性應變增量Δεn+1。

本文中心穿透裂紋船體板僅承受單軸循環載荷作用，故在單軸循環應力作用下第n+1次循環后裂紋尖端累積塑性應變增量與該次循環下塑性應變增量關系如下：

由（5）～（7）式可得經過n+1次循環后累積遞增塑性應變為：

故（8）式即為經過n+1次循環后中心穿透裂紋船體板在裂紋尖端位置處的累積遞增塑性應變值。

由（3）式和（8）式可知，本文結合船舶結構在航行過程中承受的低循環高應力外載荷條件，以中心穿透裂紋船體板為研究對象，建立了基于裂紋尖端局部區域累積遞增塑性應變的CTOD計算模型。

2 數值分析及討論

采用大型有限元軟件ANSYS對船體板進行有限元計算。在進行有限元模擬時，采用8節點PLANE82號單元進行網格劃分，材料本構關系模型選用Chaboche非線性強化準則。船體板幾何模型及其有限元計算網格模型如圖1所示，2L為缺口板長度，2W為缺口板寬度，2a為缺口板裂紋長度，裂紋尖端局部區域采用奇異網格單元并在局部區域進行網格細化處理。有限元模型中選取船體板常用304號鋼材，其相應材料參數選取如表1所示。

表1 304鋼的應變疲勞參數Tab.1 Material parameters of 304 stainless steel

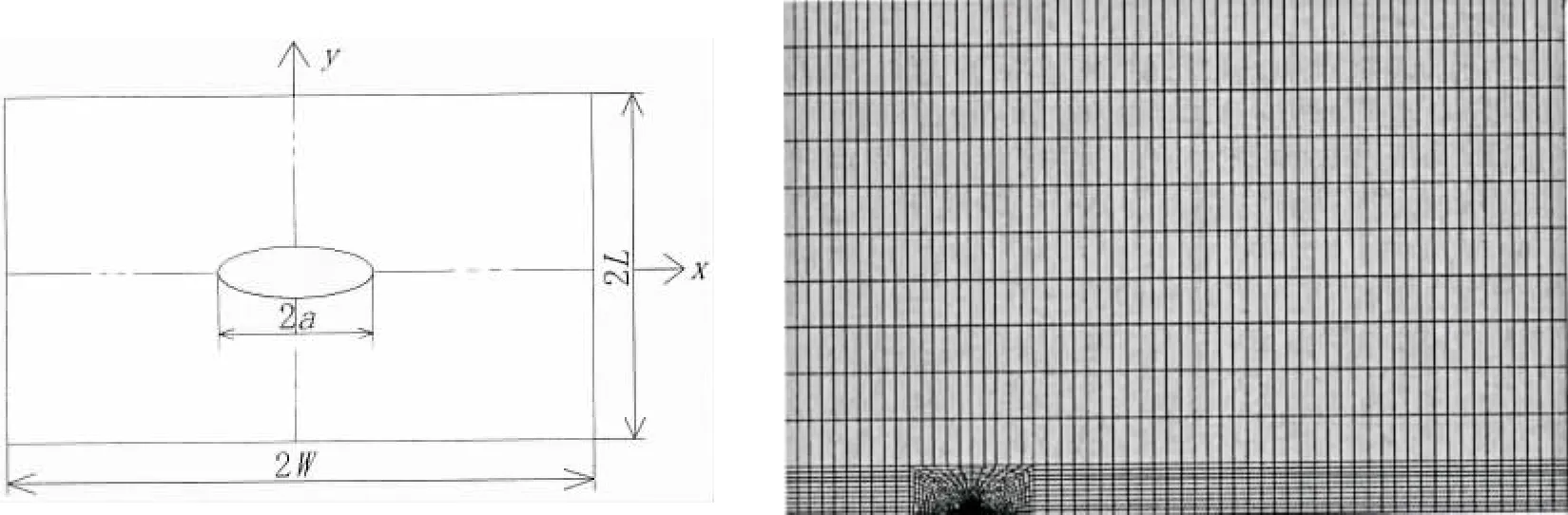
圖1 船體板的幾何模型及1/4有限元模型Fig.1 Geometry model and finite element model of ship plate with central through crack

2.1 循環載荷下裂紋尖端應力應變曲線

通過數值分析，基于Chaboche模型得到船體板在循環載荷作用下其裂紋尖端應力應變遲滯回線如圖2所示。從圖2中可以看出，在循環載荷作用下，隨著循環次數的增加，船體板裂紋尖端附近區域產生了明顯的塑性應變的累積增加。

2.2 船體板累積塑性與循環次數關系曲線

對圖1給出的船體板的有限元模型，分析應力比和應力幅的變化研究，其對裂紋尖端累積塑性應變的影響。在計算中選取 L=150 mm，W=130 mm，a=10 mm。 變更應力比 R=0.1，R=0.2和 R=0.3，應力幅 σa=240 MPa，σa=260 MPa和 σa=280 MPa。 經過系列有限元計算，得出不同應力比和不同應力幅下裂紋尖端累積塑性應變隨循環次數的變化關系曲線如圖3和圖4所示。

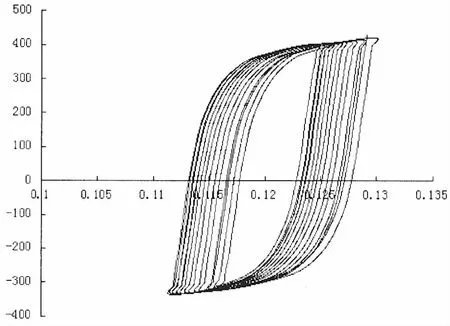
圖2 基于Chaboche循環塑性模型的裂紋尖端應力應變曲線Fig.2 The stress-strain curve near the crack tip of Chaboche cyclic plastic model

圖3 不同應力比下累積塑性應變隨循環次數變化曲線Fig.3 The curve of accumulative plastic strain vs cyclic number under different stress ratio

圖4 不同應力幅下累積塑性應變隨循環次數變化曲線Fig.4 The curve of accumulative plastic strain vs cyclic number under different stress amplitude

從圖3和圖4可以看出，當應力比或應力幅一定時，裂紋尖端累積塑性應變隨循環次數的增大而逐漸增加并趨于穩定。隨應力比或應力幅的增大，裂紋尖端累積塑性應變也增加，表明循環載荷下應力比和應力幅對裂紋尖端累積塑性變形影響較大。

2.3 船體板裂紋尖端張口位移與循環次數關系曲線

對圖1給出的船體板的有限元模型，分析應力比和應力幅的變化，研究其對裂紋尖端張口位移的影響。在計算中選取L=150 mm，W=130 mm，a=10 mm。變更應力比R=0.1，R=0.2和R=0.3，應力幅σa=240 MPa，σa=260 MPa和σa=280 MPa。經過系列有限元計算，得出不同應力比和不同應力幅下裂紋尖端張口位移隨循環次數的變化關系曲線如圖5和圖6所示。

從圖5和圖6可以看出，當應力比或應力幅一定時，循環載荷下中心穿透裂紋板CTOD隨循環次數的增加而逐漸增大并趨于穩定；隨應力比或應力幅的增大，裂紋尖端CTOD也隨之增加，說明循環載荷下應力比和應力幅對裂紋尖端CTOD影響較大。

圖5 不同應力比下CTOD隨循環次數變化曲線Fig.5 The curve of CTOD vs cyclic number under different stress ratio

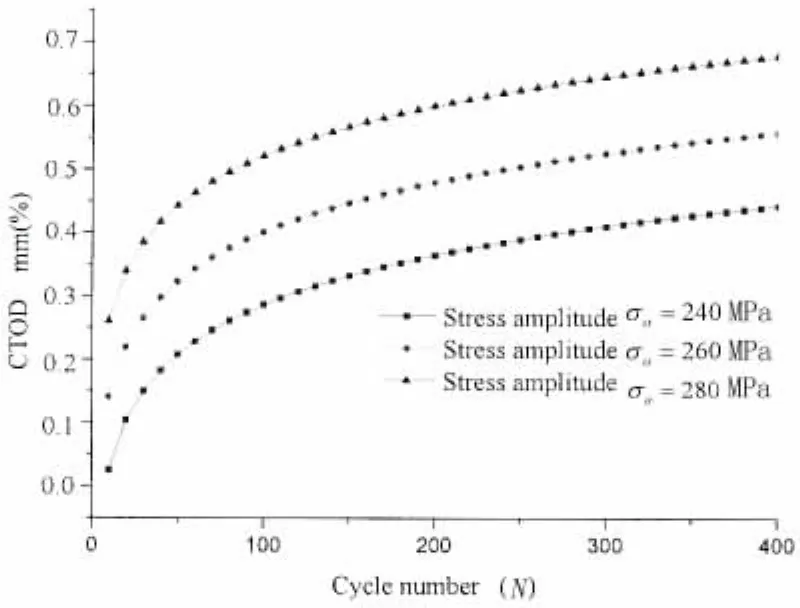
圖6 不同應力幅下CTOD隨循環次數變化曲線Fig.6 The curve of CTOD vs cyclic number under different stress amplitude

3 循環載荷下CTOD與裂紋尖端累積塑性應變間的關系曲線

由（3）式可知，在平面應力狀態下，船體板在循環載荷作用下其裂紋尖端張口位移變化量ΔCTOD與累積遞增塑性應變Δεp存在一定的函數關系。本文對圖1給出的模型在循環載荷作用下，研究應力比、應力幅的變化對ΔCTOD和Δεp關系曲線的影響。

3.1 應力比影響

考慮循環載荷下應力比R對船體板ΔCTOD和Δεp間函數關系的影響時，選取應力比分別為R=0.1，R=0.2和R=0.3，應力幅σa=240 MPa。在材料參數保持不變的情況下分別計算裂紋尖端張開位移ΔCTOD和裂紋尖端累積塑性應變Δεp，經過系列有限元計算得到的數據值如圖7所示，并與（3）式的結果進行對比。

圖7表明，在應力比和應力幅保持不變時，在循環載荷作用下船體板其裂紋尖端張開位移CTOD隨著累積塑性應變增加而增大。在應力幅一定，應力比增加時，其趨勢亦是如此。理論結果與有限元預測結果基本重合，分散性較小，說明其具有一定的可行性和較高的預測精度。

圖7 不同應力比下CTOD隨累積塑性應變變化曲線Fig.7 The curve of CTOD vs accumulative plastic strain under different stress ratio

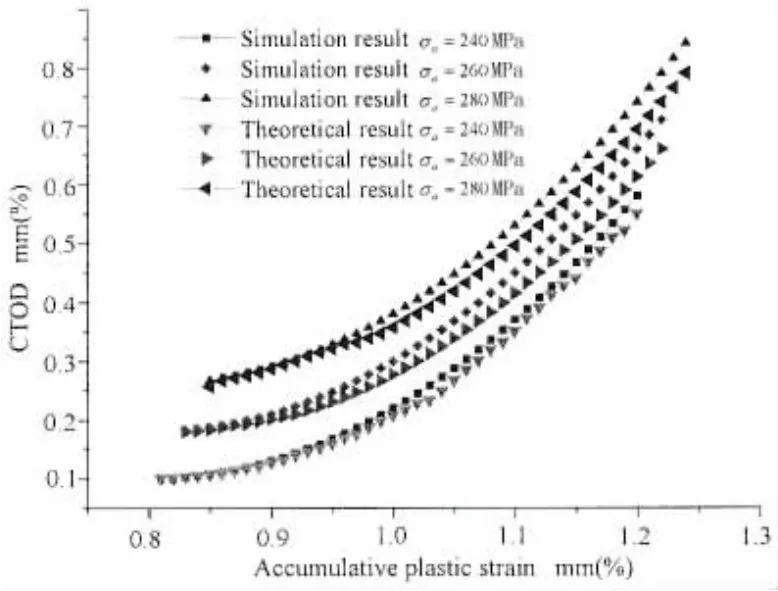
圖8 不同應力幅下CTOD隨累積塑性應變變化曲線Fig.8 The curve of CTOD vs accumulative plastic strain under different stress amplitude

3.2 應力幅影響

考慮循環載荷下應力幅σa對船體板ΔCTOD和Δεp間函數關系的影響時，選取應力幅值分別為σa=240 MPa，σa=260 MPa，σa=280 MPa，應力比R=0.1。在材料參數保持不變的情況下分別計算裂紋尖端張開位移ΔCTOD和裂紋尖端累積塑性應變Δεp，經過系列有限元計算得到的數據值如圖8所示，并與（3）式的結果進行對比。

圖8表明，在應力幅和應力比保持不變時，在循環載荷作用下船體板其裂紋尖端張開位移CTOD隨著累積塑性應變增加而增大。在應力比一定，應力幅增加時，其趨勢亦是如此。理論結果與有限元預測結果基本重合，分散性較小，說明其具有一定的可行性和較高的預測精度。

4 結 論

本文基于彈塑性斷裂力學理論，從循環J積分著手，以裂紋尖端累積塑性應變為重要參量，建立循環載荷下船體板CTOD理論模型，并在有限元模擬中分析了應力比、應力幅等相關因素影響，得到了如下結論：

（1）在循環載荷作用下，裂紋尖端局部區域將產生塑性應變的累積，隨著循環次數的增加，裂紋尖端的累積塑性應變將逐漸增加并最終趨于穩定。

（2）研究表明：應力比、應力幅值對裂紋尖端張開位移-累積塑性應變關系曲線影響較為明顯。任其中一者保持不變，另外一項增加時，船體板裂紋尖端張開位移隨裂紋尖端累積塑性應變的增加而增大。這一趨勢與理論結果吻合較好。

參 考 文 獻：

[1] Hutchinson J W.Fundamentals of the phenomenological theory of nonlinear fracture mechanics[J].Journal of Applied Mechanics,1982,49：103-197.

[2]Dugdale D S.Yielding of steel sheets containing slits[J].Journal of the Mechanics and Physics of Solids,1960,8：100-108.

[3]Cottrell A H.Mechanisms of fracture,the 1963 Tewksbury lecture[R].Tewksbury：Tewksbury 146 SymPo.On Fracture,1963：1-27.

[4]Yaowu S,Siying S,Hidekazu M.Finite element analysis on relationships between the J-integral and CTOD for stationary cracks in welded tensile specimens[J].International Journal of Pressure Vessels and Piping,1998,75：197-202.

[5]Jiang Cuixiang.Research on fracture and crack arrest in ship structures[D].Wuhan：Ph.D.Dissertation of Huazhong University of Science and Technology,2005.

[6]Potirniehe G P,Daniewiez S R.Analysis of crack tip plasticity for microstructurally small cracks using crystal plasticity theory[J].Engineering Fracture Mechanics,2003,70：1623-1643.

[7]Wu F W,Ibrahim R N,Das R.Fracture toughness for CNT specimens from numerically obtained critical CTOD values[J].Theoretical and Applied Fracture Mechanics,2009,52：50-54.

[8]Chen Jingjie.Strength analysis method research of cracked ship structure[D].Dalian：Dalian University of Technology,2011.

[9]Chen Jingjie,Huang Yi.A study on evaluation method of crack tip reverse plastic zone size for the center cracked steel plate model under tension-compression cyclic loading[J].Engineering Fracture Mechanics,2015,133：138-151.

[10]Schwalbe K H.The crack tip opening displacement and J integral under strain control and fully plastic conditions estimated by the engineering treatment model for planes tress tension[J].Fracture Mechanics,1994,24：636-651.

[11]Linkens D,Formby C L.Astrain-based approach to fracture assessment-example applications[C]//Fifth International Conference on Engineering Structural Integrity Assessment.Cambridge,2000：45-52.

[12]Jayadevan K R,?stby E,Thaulow C.Strain-based fracture mechanics analysis of pipelines[C]//International Conference on Advances in Structural Integrity.Indian Institute of Science,Bangalore,India,2004：1352-1359.

[13]Shimanuki Hiroshi,INOUE,Takehiro.Study on the CTOD estimation method of the crack in stress concentrated area[C].Japan Welding Association Conference Proceedings,2007,25(l)：230-237.

[14]Bjerke S L,Scultori M.DNV’s strain-based fracture assessment approach for pipeline girth welds[C].International Offshore and Polar Engineering Conference,19-24,2011,21：690-697.

[15]Yi D K,Xiao Z M.One elastic-plastic fracture behavior of a bi-layered composite plate with a sub-interface crack under mixed mode loading[J].Composites Part B：Engineering,2014,60：60-73.

[16]?stby E,Jayadevan K R,Thaulow C.Fracture response of pipelines subject to large plastic deformation under bending[J].International Journal of Pressure Vessels and Piping,2005,82(3)：201-215.

[17]Zhang Y M,Xiao Z M.Strain-based CTOD estimation formulations for fracture assessment of offshore pipelines subjected to large plastic deformation[J].Ocean Engineering,2014,91：9164-72.

[18]Shih C F.Relationship between the J-integral and the crack opening displacement for stationary and extending cracks[J].Journal of the Mechanics and Physics of Solids,1981,29(4)：305-326.

[19]Hutchinson J W.Singular behavior at the end of a tensile crack in a hardening material[J].Journal of the Mechanics and Physics of Solids,1968,16：13-31.

[20]Rice J R,Rosengren G F.Plane strain deformation near a crack tip in a power-law hardening material[J].Journal of the Mechanics and Physics of Solids,1968,16：1-12.

[21]Shih C F.Tables of Hutchinson-Rice-Rosengren singular field quantities[R].MRL E-147,Materials Research Laborato ry,Brown University,1983.

[22]Kumar V,German M D,Shih C F.An engineering approach for elastic-plastic fracture analysis[R].Electric Power Research Institute(Report),EPRI NP,var paging,1981.

[23]Heitmann H H,Vehoff H,Neumann P.Life prediction for random load fatigue based on the growth behavior of microcracks[J].Fracture,1984,12：3599-3606.

[24]Newman J C.A crack opening stress equation for fatigue crack growth[J].International Journal of Fatigue,1984,24：131-135.

[25]Hu Guijuan.Plastic behavior of metals under tension-torsion loading-experimental and numerical research on yield surface evolution[D].Doctor of philosophy degree thesis,Guangxi：Guangxi University,2012.

[26]Landgraf R W,Morrow J.Determination of the cyclic stress-strain curve[J].Journal of Materials,1969,4(1)：176.

[27]Noroozi A H,Glinka G,Lambert S.A two parameter driving force for fatigue crack growth analysis[J].International Journal of Fatigue,2005,27：1277-1296.