基于拍賣算法的相控陣雷達任務調度方法

李 波, 周靜楊, 高曉光

(西北工業大學電子信息學院, 陜西 西安 710129)

0 引 言

相控陣雷達(phased array radar,PAR)是一種通過改變雷達波相位從而改變波束方向的雷達,其利用陳列天線實現波束在空間的電掃描。與傳統的機械掃描雷達相比,PAR掃描速度與掃描范圍更大,波束位置、波束照射時間、次數等均更為靈活多變,其抗干擾性能和環境適應能力也更為優秀[1]。因此,PAR能夠實現搜索、多目標跟蹤、制導等多項任務同時進行,為了更加有效合理地分配雷達資源,達到雷達的最大工作效能,需要設計雷達的任務調度方法。

相比于模板法、部分模板法等常見的PAR調度方法,自適應調度策略是最為有效且復雜的調度方法[2]。文獻[3-6]在經典的最小截止期優先(earliest deadline first,EDF)算法上提出了修正的EDF模型,并在其基礎上提出了PAR實時駐留的自適應調度算法。文獻[7-8]利用“時間窗”增加了任務調度的時間靈活性。文獻[9]提出了駐留時間可變調度算法,進一步提高了任務調度能力。文獻[10]針對調度過程中因采樣周期不同在時間上產生沖突的問題,提出了基于周期分區的時間調度算法。文獻[11-12]提出了脈沖交錯算法,進一步提高了對時間資源的利用率。文獻[13-15]提出了基于遺傳算法(genetic algorithm,GA)的自適應調度方案,在分析雷達約束條件的基礎上,設計相應的編碼方式和遺傳操作。

EDF算法雖然提高了時間利用率,但是不能保障高優先級的任務調度成功率;GA雖然能夠提供較好的解決方案,但迭代次數較多,實時性能較差。拍賣算法(auction algorithm,AA)也能解決此類非確定多項式問題(non-deterministic polynomial, NP),并能達到更好的實時性要求,例如文獻[16-17]提出利用AA來解決任務分配問題,文獻[18]提出在AA相比于GA更適用于解決時間約束條件下的目標分配問題。本文提出基于AA的PAR自適應調度方案,將任務執行時間與期望執行時間的標準差作為競拍者的競標期望值,最大剩余連續時間和任務優先級作為拍賣條件,以時間作為競拍物品,求能夠使拍賣者和競拍者的社會福利最大的分配方案。仿真結果表明本文算法在具有良好的任務調度成功率和時間偏移率的前提下,可以根據實際事態需求調整加權系數來提高時間利用率或高優先級的任務調度成功率。

1 任務模型及優先級設計

1.1 任務模型

在調度間隔長度為L的時間內,有N個雷達波束駐留任務,其中單個駐留任務為

mj={Pji,tje,tjl,tjw,tjp,mjs,(Rj,αj,βj)}

(1)

式中,Pji表示任務工作優先級;由時間窗的概念可知任務有最早執行時間tje和最晚執行時間tjl。即在時間[tje,tjl]內還未被執行,則該任務被終止;tjw表示期望執行時間;tjr表示實際執行時間;tjp表示任務駐留時間;mjs為更新率即任務自動生成周期；(Rj,αj,βj)為期望波束位置。

1.2 任務優先級

基于固定優先級的調度算法是一種常見的PAR自適應調度算法,其固定優先級如表1所示。在這種固定優先級算法中,相同工作方式的調度順序只取決于時間窗和期望執行時間。不同的工作方式優先級不同,但對于多功能PAR,工作方式不能作為確定任務優先級的唯一指標,因為相同的雷達工作方式下的不同任務也會有著不同的重要程度[19-20]。不同的跟蹤任務,其目標的類型、方位、速度、加速度,都對目標威脅程度的評判有著重要影響。同時,目標的航跡質量可以用來評判目標的優先級,航跡質量越好,目標跟蹤狀態越好,目標優先級則可以相應地降低。

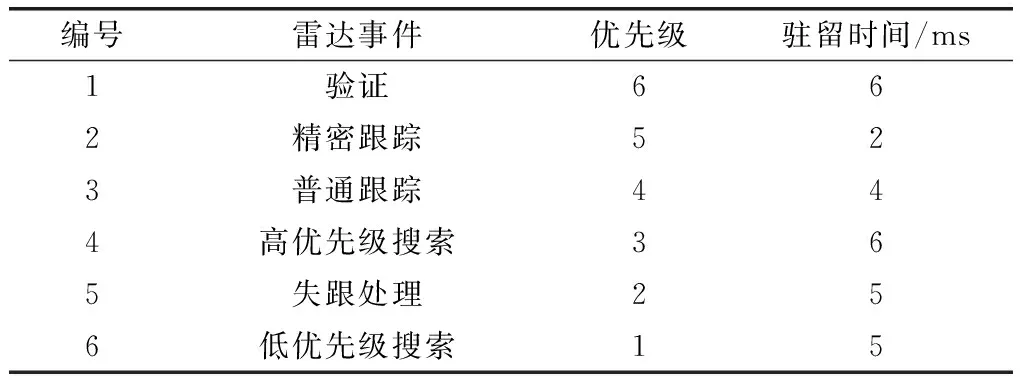
表1 雷達主要任務表

本文在優先級表的基礎上,加入目標的方位、速度、加速度及航跡質量這些要素設計一種綜合優先級。具體方法是通過將以上4個要素量化并加權,將跟蹤任務優先級細化,同時為了保證細化后的優先級不能越級超出其本身優先級,對其加權系數進行約束，即

(2)

式中，D0=D/Dmax,D為該追蹤任務的目標距離;Dmax為任務中所有目標中的距離最大值;同理,將該任務的目標速度V0、加速度a0、航跡質量Y0與所有任務中該項的最大值做比,以進行歸一化處理。δ1、δ2、δ3、δ4為不小于0的常數。n為該任務在優先級表(即表1)中的優先級。

2 調度算法

PAR任務調度策略主要解決在一個調度間隔內如何分配有限的時間資源,使得PAR能夠合理地、優化地滿足處于飽和狀態下的任務調度請求[21-25]。從這點考慮,可以將PAR資源調度問題作為時間的分配問題來求解。近來AA在資源分配問題上被廣泛應用,本文采用AA對任務PAR時間資源進行分配。

2.1 算法基本思想

進行雷達任務調度時,有以下3個原則:①根據優先級原則,當多個任務競爭同一時間槽時,優先級高的優先安排。②為了充分利用時間應盡量為后續任務留出最大連續空閑時間段,避免分割時間[25]。③為了使雷達的跟蹤精度達到最優化,根據期望時間原則,雷達系統給某任務安排的真實執行時間應盡量逼近該任務申請的期望執行時間。

雷達任務的真實執行時間應盡量逼近此雷達任務申請時的期望執行時間,這有利于跟蹤雷達精度的最優化。AA由拍賣者和競拍者構成拍賣機構,拍賣者提供拍賣物品由競拍者競價,競拍者根據自身情況決定加價或退出本輪拍賣,拍賣者不斷更新競拍者給出的最高價,直到參加拍賣的競拍者只剩一位,最高價不變拍賣停止。根據貪婪原則,拍賣者對物品進行拍賣時會追求利潤最大化,即只追求物品拍賣后所得的最高價值。競拍者根據自身信息對物品進行估價,不盲目競價,同時也不輕易放棄競價。綜合上述AA的特性,結合雷達任務調度的3個原則。算法以時間作為拍賣物品,以待調度雷達任務為競拍者。將原則①和原則②作為拍賣條件,建立競拍價值函數。競拍者的優先級越高,拍賣后剩余的連續時間越長,拍賣者獲得的利潤越高。將原則③作為競拍者的競標期望,建立競標期望函數,雷達調度任務競拍到的時間越是逼近其期望執行時間,雷達調度任務的獲利越高。

2.2 調度算法設計

設在某一調度間隔為T=[t0,t1]的時間段內,有未調度任務集合M={m1,m2,m3…mn},其中調度間隔T為拍賣者,拍賣[t0,t1]上的時間。

未調度任務集合M內的調度任務為競拍者。

下面給出本調度算法中的兩個定義。

定義1在時間段T上,已經被調度任務競拍得到并占用的時間段為占用段,競拍并得到其時間段的調度任務為已定任務nj。時間段T上的占用段集為Td。

定義2在時間段T上,由屬于調度任務mj時間窗內的任一時間點ti,作為調度任務mj的實際執行時間,能夠使任務mj執行完畢,即[ti,ti+tjp]上的所有點均在時間段T上且均不屬于占用段集Td,則稱ti為任務mj在時間段T上的飽和點,否則稱ti為任務mj在時間段T上的缺失點。任務mj在時間段T上的所有飽和點,稱為任務mj在時間段T上的飽和集Bj。任務mj在時間段T上的所有缺失點,稱為任務mj在時間段T上的缺失集Qj。

2.2.1 確定競拍價值函數

為了評估各調度任務給出的競拍價,在上述PAR調度原則①和原則②的基礎上,建立在某一調度間隔內單個雷達任務的競拍價值量(auction value),用Vj表示為

Vj=fj(pj,Δtj)

(3)

式中,f(·)為價值量函數;pj表示參與競拍的調度任務mj的任務優先級;Δtj為最大連續剩余時間,即調度任務mj競拍到時間段T上的時間后,將原時間段分割成兩個時間段中較大的那個時間段。

Δtj的求法:設在調度任務mj競拍到時間段T上的時間后其任務執行時間為ti,則有

(4)

若在時間段T上,ti的前后均存在占用段,則占用段上的任務分別記為nT-1和nT+1,如圖1所示。

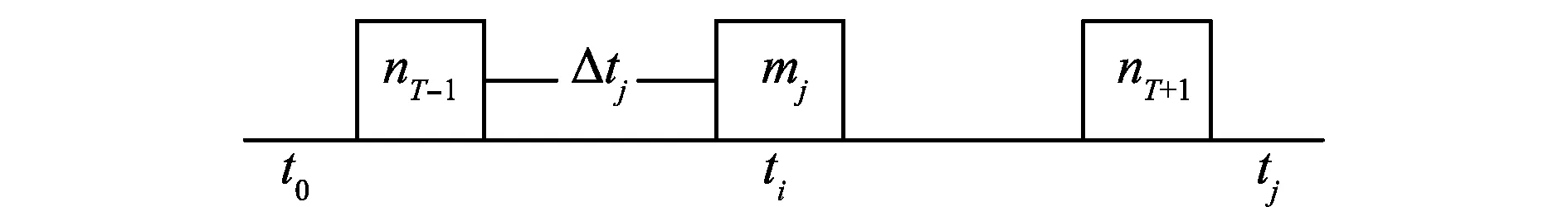
圖1 最長連續時間示意圖Fig.1 Diagram of the longest continuous time

此時,可知式(3)也可化為

Vj=fj(pj,ti)

(5)

根據上述任務優先級原則和最大連續時間原則可以得出,價值函數f(·)應隨任務優先級的變大和最大剩余時間的變長而增加,反之變小。f(·)可以通過將任務優先級量化和最大剩余連續時間量化并加權得到,即

(6)

式中,a,b≥0,a+b=1,a和b為加權系數。當a越大b越小,pj對Vj的影響越大,Δtj對Vj的影響越小;當a為0 時,pj對Vj沒有影響;當b為0 時,Δtj對Vj沒有影響。

2.2.2 確定競標期望函數

在競標過程中,競拍者對于不同的拍賣品獲取期望是不同的,同樣,在本算法中,調度任務mj對時間段T上時間點的獲取期望也是不同的。根據原則(3)可知,時間點ti距離調度任務mj的期望時間越近，其相對于任務mj的價值越高,任務mj獲取ti的期望越高。因此取調度任務mj對于時間段T上的時間點ti的獲取期望函數為

(7)

式中,使Pj最大的ti稱為調度任務mj在時間段T上的最佳時間點tjb,[tjb,tjb+jp]稱為最佳時間段。

2.2.3 調度流程

設本輪拍賣是對時間段T進行的第K輪拍賣,每輪拍賣只確定一個已定任務。第K輪拍賣過程如流程圖2所示。

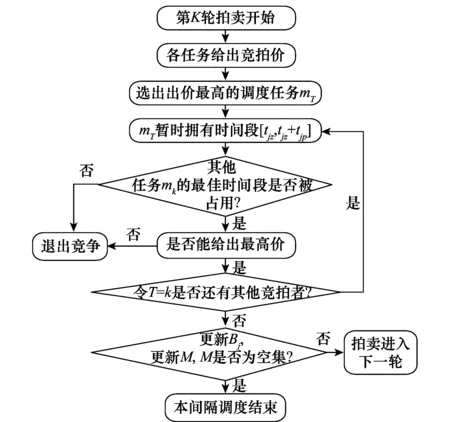
圖2 拍賣流程圖Fig.2 Flow chart of auction

詳細步驟如下。

步驟1求出未調度集合M中所有任務在時間段T上的最佳時間點tjb以及最佳時間段[tjb,tjb+jp]。并給出各自在最佳時間點的競標價fj(pj,tjb)。

步驟2找到給出最高競標價fj(pj,tjb)的調度任務mj,令T=j,tTz=tTb并將時間段[tTz,tTz+Tp]暫由任務mT占有。

步驟3對于任務集M中除mj以外的其他任務mk,若時間段[tTz,tTz+Tp]不包含任務mk的最佳調度時間段內的點,mk則不參與競價,否則根據mk的最佳調度時間段內的被占用點的位置分為以下4種情況:

①tkb∈[tTz,tTz+Tp]且在[tTz,tTz+Tp]上不存在一點ti使得fk(pk,ti)≥fT(pT,tTz),則任務mk退出競價。

②tkb∈[tTz,tTz+Tp]且在[tTz,tTz+Tp]上存在一點ti最先使得fk(pk,ti)≥fT(pT,tTz),則取消任務mT對時間段[tTz,tTz+Tp]的占有狀態,令T=k,tTz=ti且任務mT暫時占有時間段[tTz,tTz+Tp]。

③(tkb+tkp)∈[tTz,tTz+Tp]且在[tTz,tTz+Tp]上不存在一點ti使得fk(pk,ti)≥fT(pT,tTz),則任務mk退出競價。

④(tkb+tkp)∈[tTz,tTz+Tp]且在[tTz,tTz+Tp]上存在一點ti最先使得fk(pk,ti)≥fT(pT,tTz),則取消任務mT對時間段(tkb+tkp)∈[tTz,tTz+Tp]的占有狀態,令T=k,tTz=ti且任務mT暫時占有時間段[tTz,tTz+Tp]。

重復步驟3直至在未調度任務集合M中除mT以外的其他任務都退出競價,則轉到步驟4。

步驟4將時間段[tTz,tTz+Tp]判為mT所有,并將時間段[tTz,tTz+Tp]加入占用段集Td,令nT=mT,將mT從未調度任務集合M中移除并將nT加入已定任務集合N。更新未調度任務集合M中所有任務的飽和集Bj,若Bj=?且tjl≤t1,將任務mj從未調度任務集合M中移除并從任務隊列中刪除;若Bj=?且tjl≥t1,將任務mj從未調度任務集合M中移除并推遲到下個調度間隔中的任務集合中。

步驟5若未調度任務集合M=?,則結束拍賣,調度結束。否則,進入下一輪拍賣。

3 仿真實驗分析

本文選取以下3種雷達工作方式對算法進行仿真實驗:搜索(分為高優先級搜索和低優先級搜索);驗證;跟蹤(分為精密跟蹤和普通跟蹤)。雷達任務優先級和各任務駐留時間如表1所示,其中高優先級搜索任務和低優先級任務的任務周期為60SI,驗證任務時間窗為20SI,精密跟蹤時間窗為4SI,普通跟蹤時間窗為10SI。調度間隔取SI=50 ms,仿真時長為1 000SI。δ1、δ2、δ3、δ4分別設為0.2、0.5、0.2、0.1。

本文采取任務調度成功率、實現價值率及平均時間偏移率3項指標來衡量所設計調度算法的性能,其具體定義及評估意義如下:

(1) 任務調度成功率(scheduling success rate, SSR)為

SSR=N/M

(8)

式中,N為調度成功的任務總數;M為請求調度的任務總數。

各類事件調度成功率(SSRk)為

SSRk=Nk/Mk,k=1,2,…,n

(9)

式中,Nk為第k類雷達事件調度成功的任務數;Mk為第k類雷達事件參與調度的任務數。

設定仿真場景為雷達任務隨仿真周期的增加趨于飽和,在仿真初期逐漸將目標數目增加至150個,其中精密跟蹤數目與普通跟蹤數的比值為2∶3。分別取不同的a值,觀測本算法在不同的a值下總任務調度成功率、精密跟蹤調度成功率、實現價值率及平均時間偏移率,并與EDF算法作比較。仿真結果如圖3所示。

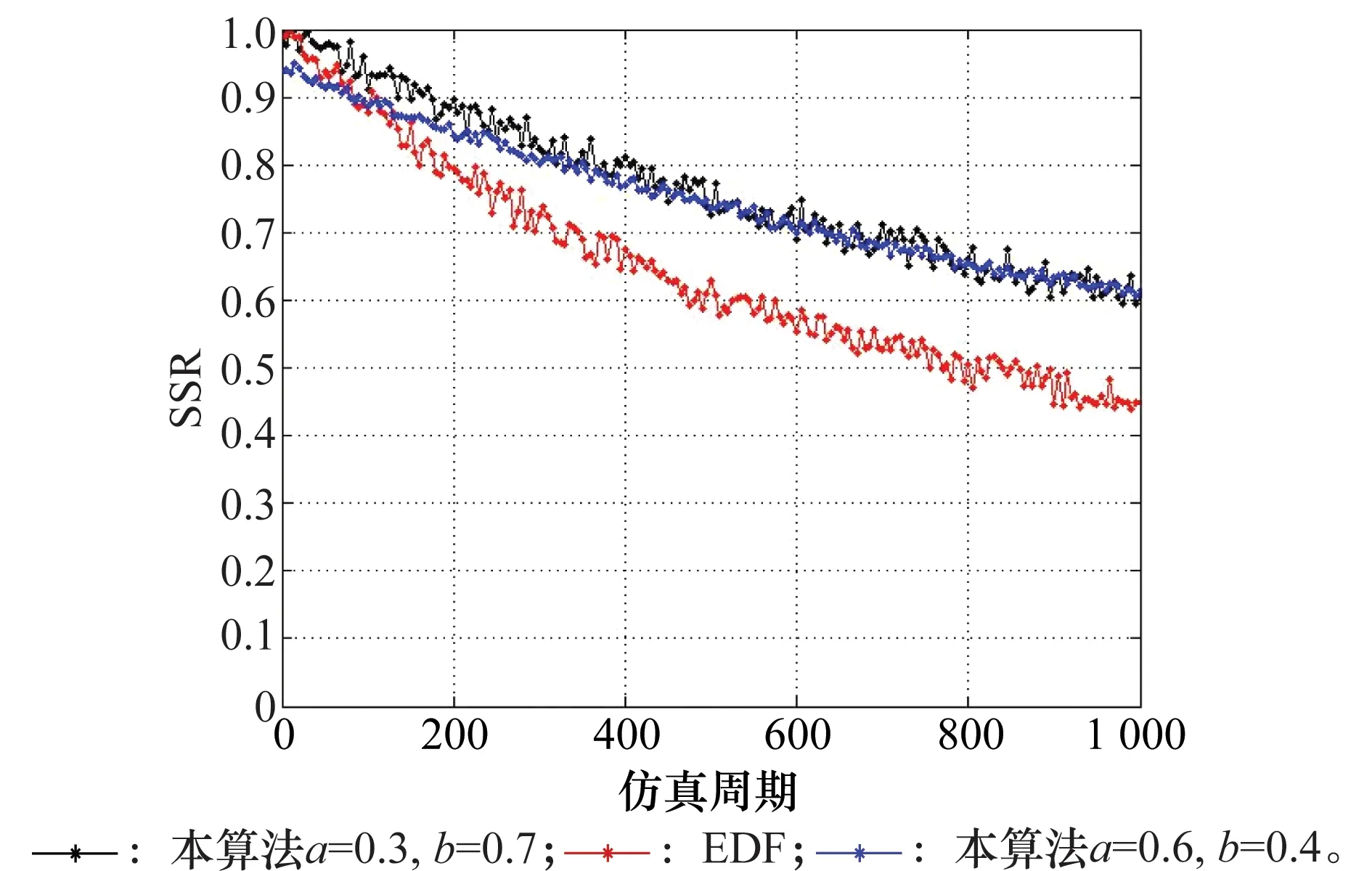
圖3 任務總調度成功率Fig.3 Success rate of task total scheduling

圖3為從仿真開始到仿真雷達周期數達到1 000的過程中,本文算法在a=0.3和a=0.6時的任務總調度成功率與EDF的任務總調度成功率對比。EDF算法表示在調度處理中,截止期越早,任務優先級越高,越優先被調度。EDF算法分為搶占式EDF調度和非搶占式調度,本文采用的是搶占式EDF調度方法。其調度的充要條件為

(10)

式中,ei和pi分別是執行時間和周期。EDF算法作為最優的單一處理器調度算法,非常適用于在雷達任務不飽和時對低優先級任務進行調度,但其調度性能在任務達到飽和后不斷下降。為了保持EDF算法在單一條件下的優良性能,本文將調度剩余時間加入到拍賣價值函數中,同樣能夠保證在任務不飽和情況下的任務調度成功率。在仿真剛開始時,雷達任務以搜索為主,調度任務處于不飽和狀態,三者皆具有良好的調度性能。但隨著仿真周期的增加,不斷有新的目標被確認,雷達任務逐漸趨于飽和,三者SSR開始下降, EDF算法由于優先級判定條件較為單一,導致不能充分利用任務調度時間窗的靈活性,因此在仿真后期調度成功率較低。而本文算法將剩余時間和時間窗均添加到調度優先級因素中,因此能夠較大限度地利用時間窗,提高本算法在飽和任務情況下的調度成功率。另外,在仿真前期本文算法在a=0.3時比在a=0.6時稍具優勢,但在仿真后期任務趨于飽和時,兩者性能相似。這是因為在仿真后期雷達調度任務主要以跟蹤為主,而a=0.6時更加側重優先保障高優先級調度。

圖4為從仿真開始到仿真雷達周期數達到1 000的過程中,本文算法在a=0和a=1時的任務調度成功率與EDF的任務調度成功率對比。

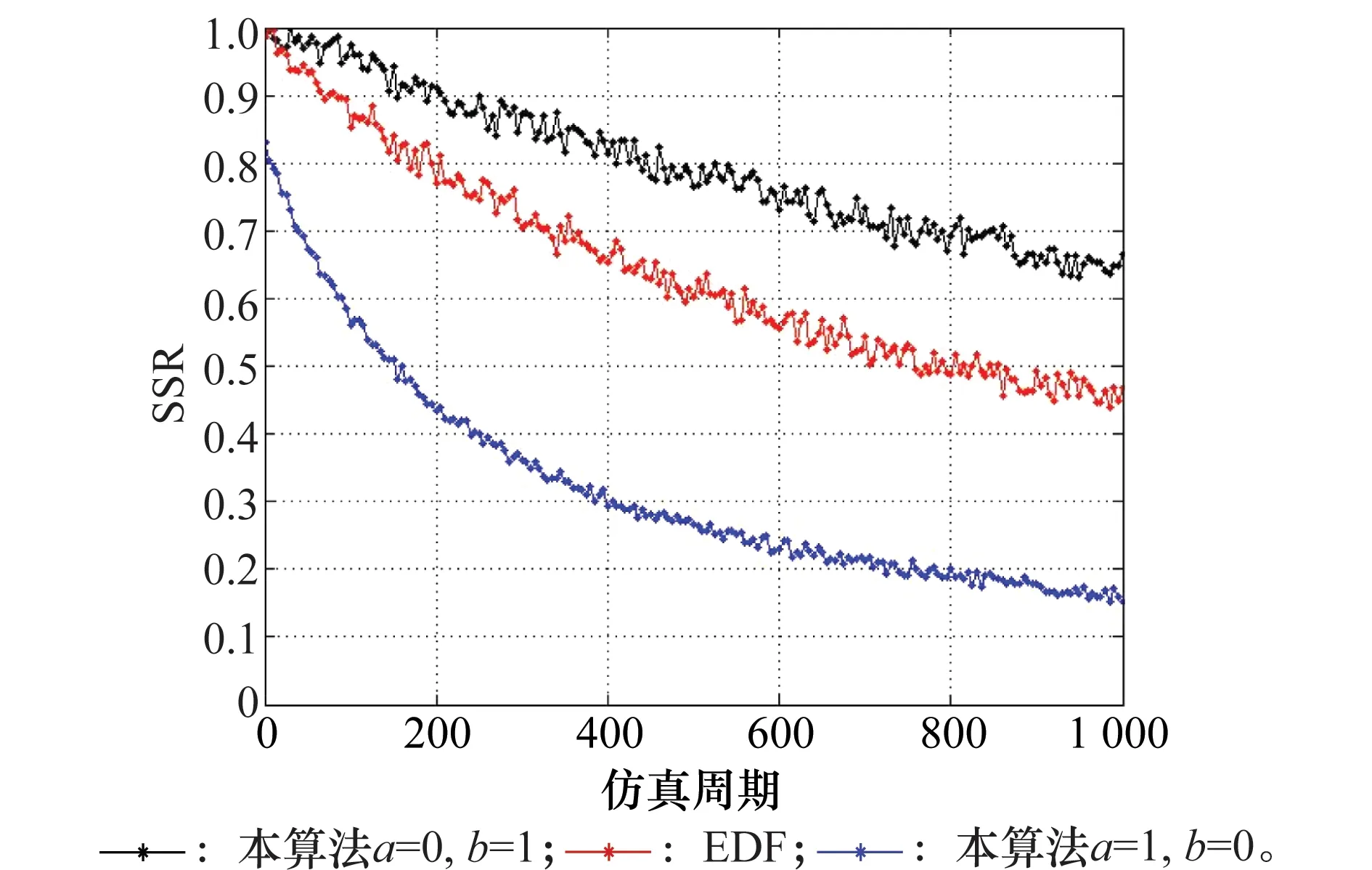
圖4 a、b取特殊值下本算法的任務調度成功率Fig.4 Success rate of task scheduling in this algorithm under the special value of a and b

當a=0時本算法的拍賣價值函數將以最大剩余時間為唯一考慮因素,剩余時間越大拍賣價值越高,這時本算法結合時間窗可以更加有效地利用調度間隔內的時間,提高算法的調度成功率。與EDF算法相比,本算法在時間利用上不但學習了EDF算法的最早截止時間優先調度思想,并且利用了時間窗概念擴充了算法的靈活性,同時結合了AA保證了算法的全局性,因此在調度任務飽和情況下相比EDF具有更高的任務調度成功率。a=1時本算法的拍賣價值函數將以任務優先級做為唯一考慮因素,優先級越大拍賣價值越高。算法雖然能夠保障高優先級的優先調度,但是由于沒有考慮時間原則,對于調度間隔內的時間利用不夠充分。因此在a=1時本算法的總任務調度成功率要比EDF算法更低。

(2) 實現價值率(hit value rate, HVR)為

(11)

式中,pi為任務i工作方式優先級。指成功調度執行的任務工作方式優先級之和與參與調度的總任務工作方式優先級之和的比值。

圖5為本算法在不同a值下的實現價值率及與EDF算法的實現價值率的比較。EDF算法由于算法設計時的針對性不同,并未將任務工作方式優先級作為任務調度的重點考慮因素,而本文算法則將任務工作優先級加入到了拍賣價值函數中。因此在調度任務處于飽和狀態下,本文算法比EDF算法具有更高的實現價值率,且提高a值可以一定程度上增加實現價值率,但過于提高a值可能會影響到算法的時間利用率,因此在提高a值的時候應注意保障算法的時間利用率。

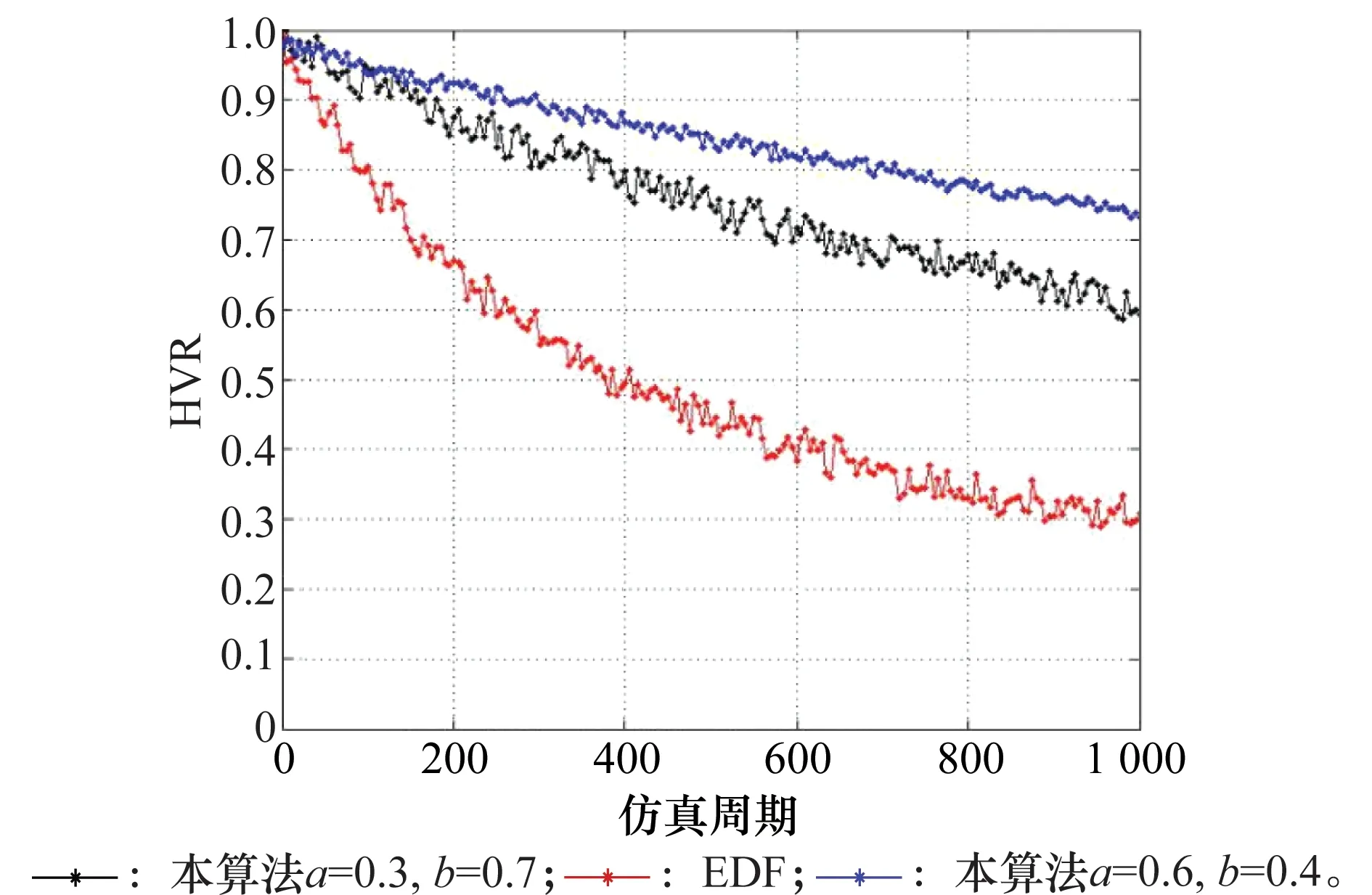
圖5 實現價值率Fig.5 Hit value rate

(3) 平均時間偏移率(average time shifting rate, ATSR)為

(12)

式中,Wi為任務時間窗長度。指各調度成功任務的實際執行時刻和期望執行時刻差的絕對值與時間窗之比的平均值。

圖6為本算法在不同a值下的平均時間偏移率與EDF算法的平均時間偏移率的比較。EDF算法將截止時間作為調度優先級的主要參考因素并未考察保證時間偏移率下的任務調度性能,而本文將期望執行時間作為本文拍賣算法的競拍價值函數,保障了算法的時間偏移率,在飽和任務下比EDF算法具有更低的時間偏移率。因此本文能夠很好地保證任務調度的及時性和算法設計的期望時間原則。

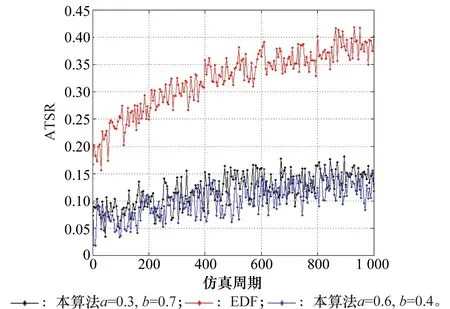
圖6 平均時間偏移率Fig.6 Average time shifting rate

4 結 論

本文針對多功能PAR任務調度中的時間資源調度問題,提出了基于AA的PAR自適應調度方案。該算法結合PAR任務調度原則,設計AA的競拍價值函數和競標期望函數。基于本文提出的設計方案和算法流程進行了仿真實驗,分析實驗結果得到,該算法在可使多功能PAR任務調度中的各指標達到優良性能。并且通過對比該算法在2種不同a的加權條件下,算法的3項性能指標,表明算法能夠通過調整加權系數來提高算法的時間利用率,并在高優先級任務的調度處理中表現出了更高的成功率。