基于信號相關性的無線傳感器網絡節點選擇方法研究*

李 孟，周榮艷

（南陽理工學院，河南 南陽 473000）

0 引 言

無線傳感器網絡中的定位問題，一般通過對傳感器陣列目標進行相關物理量如角度、距離、能量等的估計，將多個傳感器陣列估計得到的物理量進行融合，最終得到目標的位置。但是，這些方法都存在由于某一個傳感器異常測量的原因，導致最終定位出現較大的誤差。所以，需要對無線傳感器網絡中的節點進行選擇，避免某一個傳感器的較大誤差而引起的整個系統定位精度的降低。

節點選擇可以應用于目標檢測、跟蹤和定位問題中。解決不同的問題，有著不同的節點選擇方法。文獻[1-5]中，對于線性目標跟蹤系統的節點選擇問題采用的是稀疏性識別方法。對于線性測量模型，是通過一種貪心的節點選擇方法，利用子模型進行處理的[6]；對于非線性非高斯動態系統，采用枚舉優化搜索算法來解決節點選擇問題[7]；對于目標定位，采用基于信息熵的節點選擇方法[8]，但是需要目標定位的先驗概率分布信息，而對于被動聲源定位中這些信息是未知的。本文以測向交叉定位方法為例，采用聲源信號傳播的能量衰減模型，對無線傳感器網絡中一種基于信號相關性的節點選擇方法進行研究。為了驗證以信號相關性進行節點選擇的性能，將其與按節點信號的時域能量進行選擇的方法進行對比。結果表明，相較采用時域平均能量進行節點選擇的方法，采用互相關譜峰尖銳度進行節點選擇對于閾值的設定不敏感，誤差更小，性能更好。

1 測向交叉算法

測向交叉定位方法[9]通過測量方向角，利用幾何方法確定目標位置。如圖1所示，平面內的兩個傳感器陣列節點S1和S2，其間距遠遠大于傳感器節點的陣元間距。假設兩節點測得的方向角分別為θ1和θ2，從節點S1和S2沿著θ1和θ2的方向作直線，則兩條線的交點M即為目標位置。由于存在測量誤差，估計的目標位置M與真實位置N存在一定誤差。

圖1 兩節點測向交叉定位模型

當平面內的節點數目增加時，情況會更復雜。當節點數量為3個以上時，通過幾何方法確定聲源位置的計算復雜度將大大增加。此時，通常采用最小二乘法進行求解。

當有N個節點時，假設其坐標分別為(xi,yi)，估計的定向結果為θi（i=1,2,3…N），則用最小二乘法得到的目標位置為

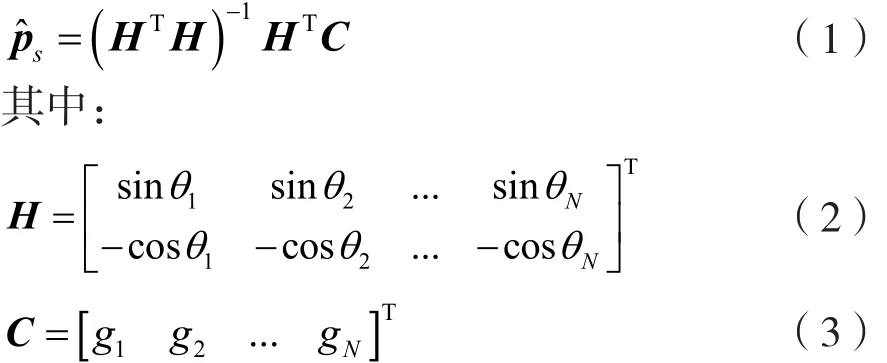
2 信號的傳播模型和節點選擇方法

2.1 傳播模型

以測向交叉定位方法為例，對節點選擇方法進行描述，并采用了聲源信號傳播的能量衰減模型[10-11]。

該模型假設如下：

（1）聲源無方向性地在均勻介質中傳播；

（2）忽略反射、折射等一系列對陣列的影響，目標聲源為點聲源；

（3）背景噪聲為高斯白噪聲，均值為零，方差已知；

（4）目標聲源能量與噪聲能量不相關。

考慮一個由N個傳感器組成的平面陣節點，第i個傳感器接收到的信號可以表示為：

其中，p和Si分別表示聲源和第i個傳感器的位置坐標。p為目標信號；vi是背景噪聲，服從均值為零的高斯分布。

2.2 基于信號相關性的節點選擇方法

假設有N個傳感器節點，節點按照任意的幾何形狀部署，每個傳感器節點有M個陣元。采用傳感器接收到的信號作互相關后的譜峰尖銳程度作為判別條件，先對時域互相關歸一化：

其中R(n)為兩個傳感器信號的離散互相關序列，R(n)歸一化是歸一化后的互相關序列，kij為第i個節點第j對傳感器互相關的幅度加和求的平均值，Ki為第i個節點所有傳感器互相關的幅度加和求的平均值的均值，Fi為Ki的倒數。設置閾值q，當Fi≥q(i=1,…,N)時，認為第i個節點符合選擇的條件。

為了驗證以信號相關性進行節點選擇的性能，將其與按節點信號的時域能量進行選擇的方法進行對比。采用傳感器接收到的信號的平均能量作為節點選擇的判別條件為：

其中，Eij為第i個節點的第j個傳感器接收到的信號能量，Ei為節點所有傳感器接收到的信號的平均能量。設置閾值k，當認為第i個節點符合選擇的條件，其估計的測向角符合角度融合的條件。

3 仿真分析

設無線傳感器網絡中傳感器節點按規則幾何位置擺放，按照矩形等間距地擺放9個陣元。目標聲源為各向同性的，按照橢圓軌跡進行逆時針運動，利用測向交叉定位方法對目標運動軌跡進行定位跟蹤。所用的每個傳感器節點為平面十字陣[12]，每對傳感器的間距為1 m。實際中，由于各個節點的信噪比不完全相同，仿真的各節點信噪比分布情況如圖2所示。采用的信號的傳播模型為2.1節中所描述的傳播模型。

圖2 各節點信噪比分布情況

同一信噪比情況下，當閾值變化時，當未進行節點選擇和節點選擇后的定位性能采用平均誤差和估計出的目標位置個數一起來度量時，即將每一個估計的目標位置與實際目標位置求距離，然后將所有距離誤差求和取平均，仿真結果如圖3所示。其中，虛線表示未進行節點選擇時的誤差，粗實線表示按互相關譜峰尖銳度選擇后的誤差，細實線表示不同閾值情況下定位出的目標位置個數。

圖3 定位精度隨互相關譜峰尖銳度閾值變化曲線

從圖3中可以看出，未進行節點選擇時定位的平均誤差在60 m左右，定位出的目標位置個數為20個。當按互相關譜峰尖銳度選擇時的閾值不斷增大時，定位誤差不斷縮小，最終趨近于0，但是其定位出的目標位置個數也在不斷減少。在閾值，定位誤差明顯下降，雖然定位出的位置個數也有所減少，但定位出了16個目標位置。當定位出的目標位置個數開始劇烈減少，這時的定位平均誤差已經不能用來衡量性能。所以，它的閾值合理范圍在20～50。可以看出，此方法擁有一個較寬的閾值范圍。

同樣的仿真條件下，對按時域平均能量進行選擇情況進行仿真，結果如圖4所示。

圖4 定位精度隨時域平均能量閾值變化曲線

其中，虛線表示未進行節點選擇時的誤差，粗實線表示按時域平均能量選擇后的誤差，細實線表示不同閾值情況下定位出的目標位置個數。從圖4可以看出，隨著閾值的不斷增加，其定位誤差沒有減小反而增大，且沒有收斂的趨勢，而其定位出的目標位置個數也在不斷減小，沒有起到提高定位精度的作用，反而比未進行節點選擇時的定位誤差還要大，最大的平均誤差達到900 m左右。

4 結 語

對于基于時延估計的無線傳感器網絡定位系統，若是采用無線傳感網網絡中的所有節點采集信息進行定位，有可能引入錯誤信息，而進行節點選擇可以有效抑制某些節點的定位誤差，從而提高定位性能。相比按時域平均能量進行節點選擇的方法，按互相關譜峰尖銳度進行節點選擇對于閾值的設定不敏感，誤差更小，性能也相對更好。當每個傳感器節點處的噪聲能量不同時，按互相關譜峰尖銳度選擇的方法更加適用。當閾值設置恰當時，還可以有效提高定位精度。