基于局部遠親差分增強的擾動粒子群優(yōu)化算法

王永貴，胡彩云，李 鑫

(遼寧工程技術(shù)大學(xué)軟件學(xué)院，遼寧葫蘆島125105)

(*通信作者電子郵箱1581280425@qq．com)

0 引言

粒子群優(yōu)化(Particle Swarm Optimization，PSO)算法是根據(jù)鳥類覓食、人類認知等社會行為提出的具有記憶功能的群智能進化算法，于1995年由Kennedy等［1］首次提出。該算法具有形式簡潔、調(diào)參靈活、收斂快速等特點，受到學(xué)者廣泛關(guān)注。目前PSO算法在多信道無線網(wǎng)絡(luò)、煤與瓦斯的測量、焊接機器人路徑規(guī)劃等復(fù)雜優(yōu)化實例中得到大量應(yīng)用［2－4］。

PSO算法僅根據(jù)個體與群體經(jīng)驗調(diào)整自身狀態(tài)，因此，個體間缺乏聯(lián)系，易逐漸喪失種群多樣性，陷入局部極值，對全局最優(yōu)解［5］搜索能力弱，在復(fù)雜多峰問題中早熟收斂問題尤為突出。為此學(xué)者們提出多種改進措施［6－7］:Li等［8］為避免粒子因單一學(xué)習(xí)模式使特定粒子缺乏智能，從而陷入局部極值，因此引入自學(xué)習(xí)粒子群優(yōu)化(Self Learning PSO，SLPSO)算法，為每個粒子提供4種不同策略應(yīng)對搜索空間中不同情況;van Zyl等［9］提出一種粒子群初始化策略解決高維問題，使粒子的搜索空間為一個子空間，而不是整個搜索空間;Guo等［10］在PSO算法中引入文化算法，群體的優(yōu)化過程是由信仰與群體兩層之間的演化與交流實現(xiàn);高衛(wèi)峰等［11］為加速算法跳出局部極值，僅對粒子搜索到的最優(yōu)解利用人工蜂群算子進行搜索，并提出基于混沌和反學(xué)習(xí)的初始化學(xué)習(xí)方法，提高了全局搜索速度;夏學(xué)文等［12］為讓算法較快逃離局部最優(yōu)，根據(jù)較差粒子及每個粒子的歷史較差位置信息指導(dǎo)粒子以較快的飛行速度進行反向?qū)W習(xí)，提高了算法的求解精度，保證了算法的收斂速度;王東風(fēng)等［13］根據(jù)粒子適應(yīng)值差異，提出一種對粒子位置進行高斯采樣均值的自適應(yīng)調(diào)整策略，增加粒子分布中心的分散度，減緩粒子在中心的聚集趨勢，并提出“鏡像墻”的越界粒子處理法，大幅提高了算法找到最優(yōu)解的概率，同時為增加種群多樣性，榜樣粒子的選擇由粒子不同進化時期的不同拓撲結(jié)構(gòu)決定;周偉等［14］在標(biāo)準(zhǔn)粒子群基礎(chǔ)上，選取精英粒子種群，構(gòu)建精英粒子群－進化融合優(yōu)化機制，并引入模糊高斯學(xué)習(xí)策略，提高了種群的多樣性和尋優(yōu)能力。

上述改進算法的性能皆有提高，但由于PSO算法本身的隨機性，若僅對算法參數(shù)改進，搜索中仍具有不確定性且無法避免陷入局部極值;若與其他算法融合，種群的每次迭代都要進行種群重建、計算、比較、尋優(yōu)，整個過程計算量大，影響算法的執(zhí)行效率。

為更好地挖掘PSO算法的搜索能力，使算法在收斂速率和收斂精度上都達到理想狀態(tài)，本文提出一種基于局部遠親差分增強的擾動粒子群優(yōu)化算法(Perturbation Particle Swarm Optimization algorithm based on Local Far-neighbor Differential Enhancement，LFDE-PPSO)。LFDE-PPSO主要有以下改進:1)為避免隨機初始化種群帶來的無效解，提出半均勻式初始化種群，使種群既不喪失隨機性又能相對均勻地遍布于搜索空間;2)為擴大粒子的搜索空間，增加解的多樣性，引入擾動因子對慣性權(quán)重、學(xué)習(xí)因子進行擾動，實現(xiàn)智能搜索;3)為提高全局搜索速度，根據(jù)適應(yīng)度值引入重構(gòu)概率，選擇部分較差個體構(gòu)建中間種群;4)為避免遺失較差個體中的優(yōu)秀基因，利用遺傳學(xué)機理，防止“近親繁殖”導(dǎo)致的無效操作，引入粒子不相關(guān)性，找到差分個體的“遠親”進行差分變異，增加種群多樣性。

1 基本理論

1．1 粒子群優(yōu)化算法

在PSO算法中，待優(yōu)化問題的潛在解可看成N維搜索空間中的一個點，即為“粒子”。粒子在N維空間中搜索，則第i個粒子的速度及位置更新如下:

表1 基本PSO算法參數(shù)說明Tab．1 Basic PSO algorithm parameter description

1．2 差分進化算法

差分進化(Differential Evolution，DE)算法［15］是一種高效智能全局搜索算法，通過個體間差分、交叉、變異產(chǎn)生新個體，增加種群多樣性，具備自學(xué)習(xí)、自組織、自適應(yīng)和全局搜索能力強等特點。DE算法主要操作如下:

1)變異操作。

2)交叉操作。

2 局部遠親差分增強的擾動粒子群算法

2．1 半均勻式初始化

為避免隨機初始化種群導(dǎo)致粒子初始化位置過于集中，不利于粒子的全局搜索，故采用半均勻式初始化種群，使種群既相對均勻地分布在整個搜索空間，又能保持種群的隨機性、多樣性。半均勻式初始化種群為:

其中:NP 為種群規(guī)模，i為第 i個個體，i=(1，2，…，NP/2);t為N維變量中第t個變量;t為第0代種群第i個粒子的第t個變量初始值。

2．2 擾動因子

在PSO算法的影響因子中，慣性權(quán)重ω是前一代粒子速度對當(dāng)前粒子速度的影響系數(shù)，平衡全局與局部搜索。自我學(xué)習(xí)因子c1與社會學(xué)習(xí)因子c2影響系統(tǒng)張力，因而許多學(xué)者對影響因子進行了不同的改進:文獻［5］采用了線性遞減策略;文獻［16］采用了非線性慣性權(quán)重遞減策略;文獻［17］提出了同步、異步的線性變換策略;文獻［18］中在學(xué)習(xí)因子中融入慣性權(quán)重的影響因素實現(xiàn)異步變換;文獻［19］采用反三角函數(shù)變換策略影響學(xué)習(xí)因子。

研究表明，對影響因子較好的改進方法是遞變策略，但固定的變換形式并不利于個體在全局范圍內(nèi)搜索，間接影響種群多樣性的保留。受自然界中蝴蝶效應(yīng)的啟發(fā)，初始條件下微小的變化能帶動整個系統(tǒng)具有長期巨大的連鎖反應(yīng)，任何事物的發(fā)展都存在定數(shù)和變數(shù)。因此，本文引入擾動因子，讓PSO算法的慣性權(quán)重和學(xué)習(xí)因子在整體遞變的基礎(chǔ)上，添加微小的變化，既防止粒子因位置變換引起速度較大的變動，又能保障影響因子在遞變的趨勢上，實現(xiàn)擾動，從而擴大解的搜索空間，使位置和速度呈現(xiàn)浮動式變換搜索，增加解的可能性。

本文擾動因子使用正余弦函數(shù)進行策略變換，因其函數(shù)值在［－1，1］變動，能夠保障影響因子實現(xiàn)小范圍內(nèi)跳動。慣性權(quán)重、學(xué)習(xí)因子變換策略為:

其中:k為迭代次數(shù);kmax為最大迭代次數(shù);rand()為(0．9，1)的隨機數(shù);αk、βk分別為正余弦擾動因子;ωk是種群k次迭代的慣性權(quán)重;ωmax、ωmin是慣性權(quán)重可取到的最大值和最小值;c1，k、c2，k為 k次迭代過程中的自我學(xué)習(xí)因子、社會學(xué)習(xí)因子;c1s、c1e為自我學(xué)習(xí)因子的初始與最終值;c2s、c2e為社會學(xué)習(xí)因子的初始與最終值。

擾動策略在算法初期，能夠使ω、c1取較大值，使粒子擁有較快的遞減速率，促進粒子進行局部搜索，加快粒子向全局最優(yōu)聚攏，并使粒子對自身具備較強的思考能力，鼓勵粒子靠近曾發(fā)現(xiàn)的最優(yōu)位置;算法后期ω遞減速率降低，c2取值較大，促進粒子間進行信息共享，幫助粒子在局部搜索的過程中實現(xiàn)精細搜索，引導(dǎo)粒子逼近全局最優(yōu)位置，保持搜索精度與速度之間的平衡。

2．3 局部遠親差分增強

PSO算法的整個尋優(yōu)過程僅由個體和社會的歷史最優(yōu)位置迭代驅(qū)動，其所有操作都僅針對優(yōu)秀個體，容易忽略群體中其他粒子信息，特別是較差個體，而較差個體與優(yōu)秀個體中的優(yōu)秀基因往往相差甚遠，這就導(dǎo)致搜索過程中對種群多樣性影響較大的優(yōu)秀基因逐漸丟失，使種群易陷入局部極值而無法跳脫。為使中間種群中較差個體的優(yōu)秀基因得以延續(xù)，本文根據(jù)遺傳學(xué)“遠親繁殖，雜交出優(yōu)勢”，引入了粒子不相關(guān)性，由粒子不相關(guān)性計算選擇概率，利用選擇概率找出“遠親”進行雜交繁殖，有效保障優(yōu)秀基因的傳承，使種群在搜索過程中保持活力，避免算法陷入局部極值。

局部遠親差分增強策略首先利用重構(gòu)概率根據(jù)輪盤賭選擇適應(yīng)度值低的個體重新構(gòu)建中間種群;然后，在中間種群中隨機選擇差分個體，根據(jù)粒子的不相關(guān)性計算其余個體的選擇概率，利用選擇概率，從中間種群中找出兩個與差分個體基因差異較大的臨時個體進行差分變異，保留適應(yīng)度值高的個體基因進入下一代種群。

1)重構(gòu)概率。

為了使算法每次的搜索結(jié)果都能有效反饋給種群，讓種群根據(jù)尋優(yōu)結(jié)果進行相應(yīng)的變換，實現(xiàn)自適應(yīng)調(diào)整，因此，本文引入重構(gòu)概率，即根據(jù)粒子的適應(yīng)度值求出粒子被選中重新構(gòu)建中間種群的概率。

其中:i=1，2，…，NP，NP為種群規(guī)模。式(11)表明當(dāng)粒子適應(yīng)度值越低，對應(yīng)重構(gòu)概率越大，即粒子被選擇構(gòu)成中間種群的可能性越大。

2)粒子不相關(guān)性。

其中:t=(1，2，…，n)，t為n維向量中具體的一維。式(12)表明，若個體間變量值差異性較大，則不相關(guān)性越大。

3)選擇概率。

3 算法流程

步驟1 初始化 PSO 算法參數(shù)，(ωmin，ωmax) =(0．4，0．9)，(c1s，c1e)=(2．5，0．5)，(c2s，c2e)=(0．5，2．5)，種群規(guī)模NP，每維變量的上下界范圍，粒子的最大飛行速度Vmax;最大迭代次數(shù) kmax，變異算子 F=0．5，交叉概率 CR=0．9;

步驟2 由式(5)半均勻式初始化種群;

步驟4 FOR i=1，2，…，NP，計算個體適應(yīng)度值與輪盤賭構(gòu)建規(guī)模為(NP/3)的中間種群;

步驟11 若k≥kmax，則輸出粒子所在位置的適應(yīng)度值，否則重復(fù)步驟3～11。

4 實驗及結(jié)果分析

為確保實驗的公平性，本文所有實驗均在Inter Core i5-2450M CPU 2．5 GHz，12 GB內(nèi)存的機器上實現(xiàn)，軟件運行的環(huán)境是Matlab 2014b。種群規(guī)模NP=30，變量維度N=30，最大迭代次數(shù)kmax=1000，每個測試函數(shù)單獨運行30次，可接受誤差為 0．1。

4．1 測試函數(shù)及評價標(biāo)準(zhǔn)

為驗證擾動策略和局部遠親差分增強策略的可行性，本文選取了2個經(jīng)典單峰函數(shù)與3個復(fù)雜多峰函數(shù)進行驗證。函數(shù)的搜索空間與理論最優(yōu)值如表2所示。其中函數(shù)1是帶噪聲的四次方緩動函數(shù)，最優(yōu)值隨隨機分布數(shù)而改變，較難尋優(yōu);函數(shù)2是單峰非凸、較難極小化的典型病態(tài)二次函數(shù)，其最優(yōu)值與多變量相關(guān)，搜尋難度較大;函數(shù)3、4、5都是旋轉(zhuǎn)、不可分離的可變維三角多峰函數(shù)，具有大量局部最優(yōu)點，算法在求解過程中容易逼近局部最優(yōu)，難以尋到全局極值。

為評定算法性能，本文選用以下評價準(zhǔn)則［19］:

1)成功率(SuccR):將適應(yīng)度函數(shù)最終解達到誤差允許范圍內(nèi)視為有效解，成功率為有效解次數(shù)占總執(zhí)行次數(shù)的比例，用來衡量算法的魯棒性;

2)平均最優(yōu)值(MeanBst):算法30次獨立運行結(jié)束后所得適應(yīng)度函數(shù)的平均最優(yōu)值，該指標(biāo)可衡量算法的尋優(yōu)質(zhì)量;

3)最終適應(yīng)度值(FinalBst):函數(shù)最終收斂時的最優(yōu)值;

4)平均運行時間(MeanT/s):算法獨立運行30次平均執(zhí)行時間，是對算法尋優(yōu)時效性的衡量;

5)穩(wěn)定性(Stab):算法獨立運行30次，所得精度標(biāo)準(zhǔn)差。

表2 測試函數(shù)信息Tab．2 Information of test functions

4．2 單項改進措施有效性驗證

為驗證LFDE-PPSO各個改進措施的有效性，先分別對單項改進措施進行驗證。

1)擾動策略。為驗證擾動策略PPSO(Perturbation PSO)可使粒子在搜索過程中有效降低粒子陷入局部極值的可能。這里將PPSO與基本PSO算法進行對比，采用測試函數(shù)f1、f5進行驗證。結(jié)果如圖1所示。

圖1 函數(shù)收斂特性曲線Fig．1 Function convergence characteristic curves

從圖1中可以看出，PPSO在單峰與多峰函數(shù)優(yōu)化上，能夠很快進入到全局最優(yōu)狀態(tài)，優(yōu)化精度、速率明顯高于基本PSO算法，充分證明擾動策略利于加快速度變換空間，避免粒子局部聚集，推動粒子在全局范圍內(nèi)搜索，有效保持種群的多樣性，能夠控制局部與全局間的搜索平衡。

2)局部遠親差分增強策略。為驗證局部遠親差分增強(Local Far-neighbor Differential Enhancement，LFDE)策略能夠增加PSO算法種群多樣性，提高算法的收斂速度，幫助粒子逃離局部聚集狀態(tài)，本文將 LFDE算法與基本PSO算法、DEPSO算法采用測試函數(shù)f2、f4進行驗證，分別從以下兩個方面進行比較:1)穩(wěn)定性驗證，比較3種算法在精度相同時適應(yīng)度值方差;2)收斂速率驗證，比較三種算法在函數(shù)評價次數(shù)相同時各自的收斂精度。實驗結(jié)果如表3所示。

從表3可知，LFDE算法與傳統(tǒng)PSO算法相比，在達到相同精度時，PSO算法在 f2、f4的 Variance是 LFDE算法的6．56E+02、3．44E+06 倍，在運行 10 000、20 000、30 000 次時，PSO算法在f2的適應(yīng)度值分別是LFDE算法的1．35E+06、4．36E+05、5．96E+04 倍，在 f4的適應(yīng)度值分別為8．05E+15、7．00E+15倍。與DEPSO算法相比，DEPSO算法在f2的三次適應(yīng)度值分別是 LFDE 算法的 2．84E+05、4．08E+04、6．24E+02倍，在f4的適應(yīng)度值分別為1．61E+12、4．84E+10倍。以上結(jié)果表明，LFDE算法與基本PSO、DEPSO算法相比，在收斂速率上明顯提高。在穩(wěn)定性方面，LFDE算法比PSO算法改善明顯，但與DEPSO算法相比，沒有明顯優(yōu)勢，尤其在單峰函數(shù)的優(yōu)化問題上，LFDE算法的適應(yīng)度值方差是DEPSO算法的1．27倍，而在多峰函數(shù)上是DEPSO算法的39．79倍，說明在穩(wěn)定性方面，LFDE算法在多峰函數(shù)的優(yōu)化問題上仍具有一定優(yōu)勢。從上述實驗結(jié)果可知，DEPSO算法與LFDE算法都能夠維持種群多樣性，這是由于DEPSO與LFDE算法都是通過交叉、變異產(chǎn)生新個體;但DEPSO算法每次迭代都通過DE與PSO算法生成兩個種群，對這兩個種群進行比較，擇優(yōu)選出Pbest與Gbest，因而算法整體計算量龐大，極大地降低了算法的收斂速率。

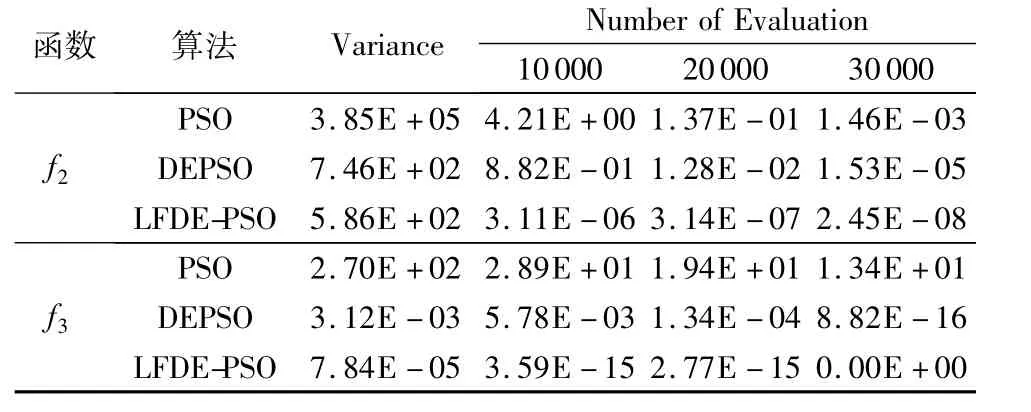
表3 3種算法多樣性、速率比較Tab．3 Diversity and rate comparison of three algorithm

以上兩個單項驗證實驗結(jié)果可以得出，本文提出的擾動策略和局部遠親差分增強策略，在算法的收斂速率和種群多樣性的維持上都具有明顯優(yōu)勢。

4．3 本文算法驗證

為進一步驗證LFDE-PPSO的優(yōu)化性能，本文將LFDEPPSO 與標(biāo)準(zhǔn)粒子群算法(Standard PSO，SPSO)［20］，以及對PSO算法改進的混沌粒子群優(yōu)化算法(Chaos PSO，CPSO)［21］、自調(diào)節(jié)粒子群優(yōu)化算法 (Self Regulating PSO，SRPSO)［22］、交錯搜索粒子群優(yōu)化算法 (Crisscross Search PSO，CSPSO)［23］進行比較。表4、5分別為這5種算法對應(yīng)單峰、多峰測試函數(shù)的實驗結(jié)果，表5中的最后一項是5種算法在5個測試函數(shù)的4項評價準(zhǔn)則的實驗結(jié)果平均值。

表4 單峰函數(shù)算法性能比較Tab．4 Performance comparison of single-peak function algorithms

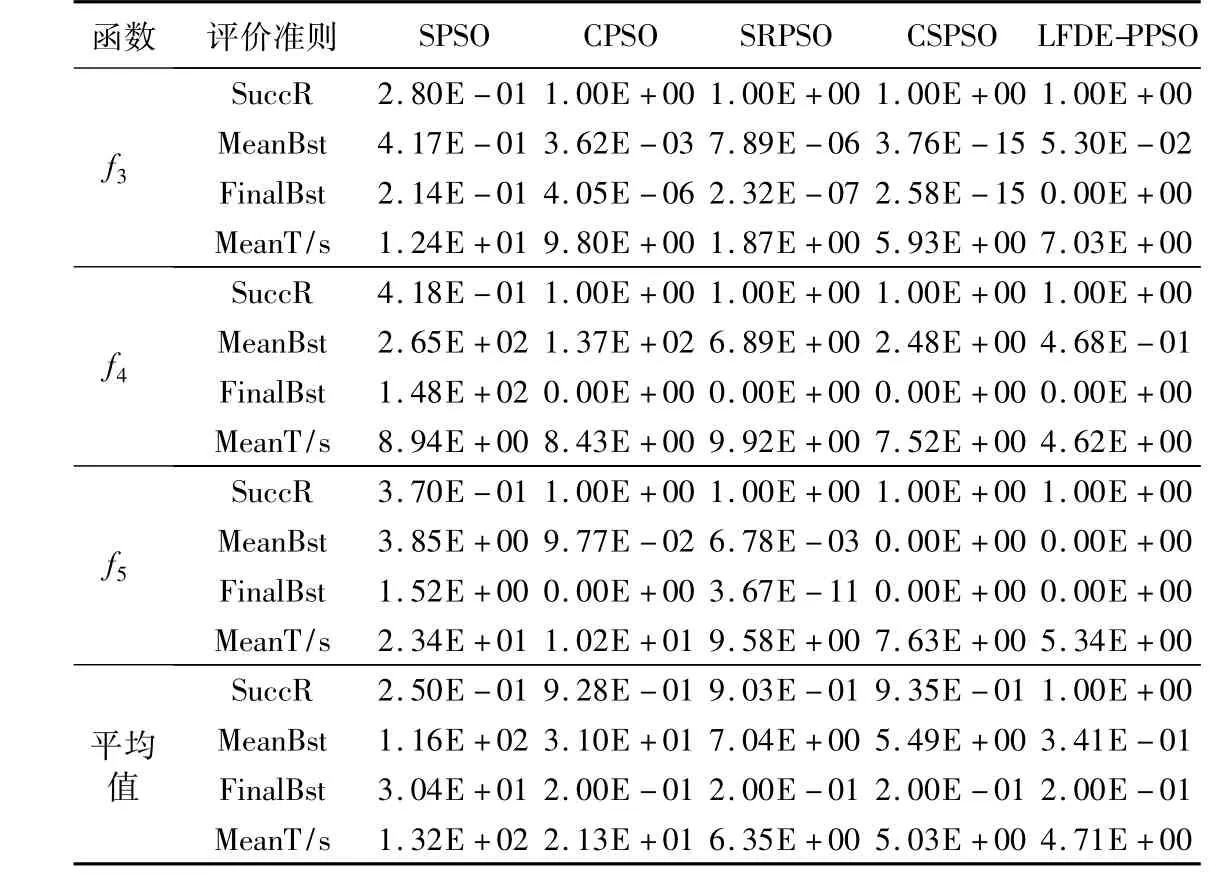
表5 多峰函數(shù)算法性能比較Tab．5 Performance comparison of multi-peak function algorithms

從表4、5中可知，上述幾種算法對f5的優(yōu)化效果都較為理想，是因為該函數(shù)當(dāng)空間維數(shù)超過15維時，函數(shù)特性轉(zhuǎn)變，趨向單峰函數(shù)，易找到最優(yōu)值。SPSO算法在f1上的MeanT/s是LFDE-PPSO的11倍;由平均值中的MeanT/s比較可知，LFDE-PPSO分別是 CPSO、SRPSO、CSPSO 算法的23．68%、74．19%、93．7%，算法的執(zhí)行效率得到極大的改善;在FinalBst上，LFDE-PPSO在平均值中是CPSO算法的99%，雖然SRPSO、CSPSO算法在FinalBst上均能達到函數(shù)對應(yīng)的極值，但在MeanBst的平均值計算結(jié)果上，分別是SRPSO、CSPSO算法的4．84%、6．21%，LFDE-PPSO 依舊具有一定的優(yōu)勢。因而，從表4、5的各項驗證結(jié)果可得出，LFDE-PPSO的尋優(yōu)精度、速率以及算法的尋優(yōu)質(zhì)量明顯優(yōu)于 SPSO、CPSO、SRPSO、CSPSO 算法。

為進一步驗證LFDE-PPSO在收斂精度和穩(wěn)定性上的性能，分別對LFDE-PPSO與SPSO算法以及綜合學(xué)習(xí)粒子群優(yōu)化算法(Comprehensive Learning PSO，CLPSO)［24］、全 局 信 息 粒 子 群 算 法 (Fully Informed Particle Swarm，F(xiàn)IPS)［25］和 CPSO 算法進行比較。圖2、3分別是算法在30次實驗中，進行1 000次迭代的平均收斂特性曲線和標(biāo)準(zhǔn)差波動圖，圖中橫縱坐標(biāo)分別是收斂精度對數(shù)、標(biāo)準(zhǔn)差與迭代次數(shù)。

由于SPSO算法無法向局部其他粒子學(xué)習(xí)，易造成啟發(fā)式信息和計算資源浪費，陷入局部最優(yōu)，算法尋優(yōu)質(zhì)量較差;CPSO算法利用混沌映射創(chuàng)建初始種群，利用最優(yōu)解附近混沌搜索結(jié)果替代種群中部分粒子，但CPSO算法是當(dāng)種群陷入局部極值后，混沌搜索策略才開始生效，尋優(yōu)過程中忽略其他粒子可能含有的先進基因，在多峰問題的求解上效果較差，從圖2中可看出，當(dāng)?shù)螖?shù)達到500次時，適應(yīng)度值曲線基本已停止尋優(yōu)，陷入互補局部極值。CLPSO算法通過選擇榜樣粒子的學(xué)習(xí)策略能夠改善PSO算法的性能，但該算法對多樣性保留的機制過于強健，在復(fù)雜多峰優(yōu)化上較為有效，而單峰問題上的求解效果并不理想，在單峰問題的求解質(zhì)量上僅優(yōu)于SPSO算法。FIPS算法利用鄰域內(nèi)所有成員最優(yōu)加權(quán)平均值指導(dǎo)更新，結(jié)合周邊粒子的信息，該算法在單峰函數(shù)優(yōu)化問題上作用效果尤為明顯，但該算法忽略個體差異性，因而在復(fù)雜多峰求解問題上效果較弱。從圖2所有的函數(shù)適應(yīng)度值曲線中可以看出，對于難以優(yōu)化的高維函數(shù)，尤其是存在多個局部極值的多峰函數(shù)，SPSO、CLPSO、FIPS、CPSO算法尋優(yōu)時易陷入局部最優(yōu)，且粒子一旦陷入局部極值，則很難跳出，因此很難得到理想的效果，LFDE-PPSO根據(jù)粒子適應(yīng)度值自適應(yīng)的選擇較差粒子重建中間種群，獲取較差個體中優(yōu)秀基因填充現(xiàn)有種群，豐富了種群的多樣性。因此，在迭代的初期能夠較快地逼近全局最優(yōu)，在單峰及復(fù)雜多峰的問題求解上都能取得優(yōu)質(zhì)解。從圖3的平均標(biāo)準(zhǔn)差波動趨向圖可以明顯得出，LFDE-PPSO與SPSO、CLPSO、FIPS、CPSO 算法相比具備較強的穩(wěn)定性能。

圖2 各算法收斂特性曲線對比Fig．2 Convergence characteristic curve comparison of algorithms

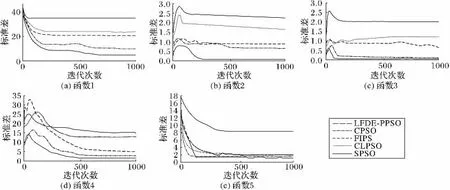
圖3 各算法標(biāo)準(zhǔn)差波動對比Fig．3 Standard deviation comparison of algorithm

5 結(jié)語

本文提出了一種基于局部遠親差分增強的擾動粒子群算法，通過多角度對比仿真實驗得出該算法具有以下特點:1)采用擾動策略，使慣性權(quán)重與學(xué)習(xí)因子在迭代過程中動態(tài)生成，并加以微小擾動，使粒子在有效位置和速度上實現(xiàn)跳動，擴大搜索范圍，平衡全局搜索和精細搜索，促進粒子跳出局部極值;2)對新生種群中較為低質(zhì)的粒子采用局部遠親差分增強策略，挖掘低質(zhì)粒子中優(yōu)秀基因，通過交叉變異保存下來，填充現(xiàn)有種群基因庫，進而使種群富有活力，不易陷入局部極值進入早熟狀態(tài);3)僅對部分個體進行差分增強操作，避免種群大規(guī)模再生，重復(fù)計算，算法的收斂速度得到了極大的提升。因此，本文算法在處理較為復(fù)雜的優(yōu)化問題上具有重要的實用價值。接下來，對于受參數(shù)影響較大的支持向量機優(yōu)化問題上，利用LFDE-PPSO自動尋找支持向量機的最優(yōu)參數(shù)，提高向量機的分類準(zhǔn)確率與速率是下一步有待研究的問題。