基于模糊邏輯的手臂運動控制小腦模型與仿真

張少白，諸明倩

(南京郵電大學 計算機學院，江蘇 南京 210003)

0 引 言

人的小腦能夠感知和控制各種各樣的運動，小腦皮質中的三層結構-分子層、顆粒層和浦肯雅細胞層對于運動控制有著至關重要的作用。皮質內存在五種神經元，它們分別是：星形細胞(stellate cell,SC)、高爾基細胞(Golgi cell,GO)、顆粒細胞(granule cells,GC)、浦肯雅細胞(Purkinje cell,PC)以及籃狀細胞(basket cell,BC)。正是這五種神經元的相互作用，才促使小腦能夠完成各種復雜的功能。

由于小腦對于運動控制的強大作用，促使很多研究人員致力于小腦模型的構建與研究，并且取得了一定的成果。首先出現了一種關于小腦功能的理論[1]。Albus修正和擴展了該理論，提出并發表了新的關于小腦功能的理論[2]，基于這一理論，Albus創建了著名的小腦模型CMAC，并成功地應用于機器人手臂協調運動控制[3]。Albus之后，相繼出現了許多關于機器人小腦模型的研究。例如，美國Illinois大學的Adams教授對小腦運動神經學習(ML)進行研究，提出了重要的假設和猜想，即小腦運動神經控制(MC)的結構是閉環的和反饋的[4-5]。日本著名學者Ito，基于自動控制原理中的內模原理，提出了小腦內模的概念并認為，內模是學習或訓練的產物[6]。美國Harvard大學教授Houk等在這一領域有諸多貢獻，他們設計了一個小腦模型，用在一個非線性的彈簧與金屬塊實驗裝置上，進行運動控制實驗[7]；后來，他們又設計了一個眼球平滑運動的小腦預測模型[8]。日本著名的機器人學者Kawato對小腦模型和機器人控制進行了深入研究，基于人工神經網絡設計了一種小腦模型，用于多關節機械臂的運動控制[9]；之后，又基于BP網絡為機器人設計了一個小腦四域計算模型[10-11]；Kawato在北京舉行的ICNNB國際會議上演示了基于小腦模型學習行走的人性化機器人，并再次闡述了機器人與動物神經系統的關系[12]。

以上學者對于小腦模型本身的研究做出了杰出的貢獻，也有另外一些學者另辟蹊徑，將模糊邏輯與傳統的小腦模型CMAC相結合，也就是在其輸入層引入模糊集合的隸屬度概念,這樣做的目的有兩個，一是為了對客觀世界進行更加真實的描述，因為模糊方法對于客觀對象的描述更具一般性；二是為了對模糊推理映射的計算以及模糊控制進行簡化，而且還增加了模糊制的學習功能，使其應用起來更加方便有效。而文中考慮到現在已經存在很多有關模糊小腦模型神經網絡的研究，但是用的都是CMAC模型，對具有仿生意義的小腦模型還未涉及，故將該理論運用于仿生小腦模型，以提高其性能。

1 模糊小腦模型

1.1 用于手臂運動控制的小腦模型

文中擬構建的小腦模型主要用于手臂運動控制，為此將對Hoff-Arbib模型進行簡單介紹，因為它是一種經典的手臂運動模型。為了對各種條件下手的預成型以及手臂運動進行相應的解釋，包括所抓取對象的位置、方向以及抓握角度的變化，Hoff和Arbib曾在文獻[13]中特地構建了一種控制模型，這種模型主要是基于最小加速度(minimumjerk)的最優標準進行構建的。模型中的手和手臂被單獨控制，而延伸與抓取之間的協調需要通過選取確定抓取角度的形成和手臂延伸到目標所需的時間這兩項中的最大值作為持續輸入信號來完成。

手臂的控制規則如下所示：

(1)

其中，x表示位置；t表示用于產生最小加速度的目標物體；D為剩余時間。

針對生物系統傳入以及傳出時存在的延時問題，文獻[14]給出了解決方案，也就是在Hoff-Arbib模型的基礎上加入了小腦模塊以及剩余時間預測部分，其中小腦模型可以用來學習被控體前向模型。

具體的小腦神經系統如圖1所示，它是具有輸入輸出連接的。該系統將目標位置、速度以及加速度通過苔蘚纖維輸入到小腦模塊，這些輸入分為五組群碼，它們來自不同的子系統。這五組群碼分別表示目標與當前位置間的位置差，當前運動命令的傳出副本，以及脊髓傳入信號的延時狀態信息，也就是位置、速度和加速度。文獻[15]中對它進行了具體的說明。而文中用于與模糊邏輯相結合并進行仿真的小腦神經系統正如圖1中所示。

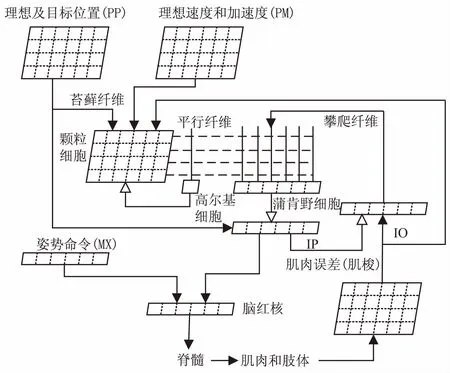
圖1 具有輸入輸出連接的小腦神經系統

1.2 模糊系統

1965年，Zadeh教授發表論文《模糊集合》(fuzzy set)，該論文的發表標志著模糊數學的誕生。模糊集合的基本思想就是把經典集合中的絕對隸屬關系靈活化，也就是元素對“集合”的隸屬度不再局限于取0或1，而是可以取從0到1間的任一數值。要實現這一點，就需要引入隸屬函數的概念，用它來描述處于中間過渡階段的事物對于差異雙方的傾向性。而隸屬度就用來表示元素屬于集合的程度。

可以將此模糊理論用于模糊控制，它是基于模糊推理、模糊語言變量、模糊集合的，其控制規則就是人類所累積的先驗知識以及專家經驗。模糊控制的重點是模擬人對系統的控制，要實現這種控制就需要在被控對象的基礎上運用模糊控制器進行近似推理等手段。在此期間需要著重考慮的是如何確定模糊變量的隸屬度函數，以及如何制定相應的控制規則。

與傳統控制相比，模糊控制存在許多優勢，比如它適于解決非線性系統的控制問題，具有良好的魯棒性以及自適應性，可以用于時變、時滯系統，而這些優勢均是由于模糊控制只需要根據相關的規則與數據進行設計，而不需要精確的數學模型。

模糊系統的核心是知識庫，它存儲了有關模糊控制器的一切知識，其中包含具體應用領域中的相關知識以及要求的控制目標，這些知識對于模糊控制器的性能起著決定性作用。

1.3 模糊神經網絡

模糊系統和神經網絡之間存在著一些明顯的區別與聯系。第一它們對于知識的表達方式不同，模糊系統可以用來表達人類總結的一些經驗性知識，這樣更方便于人們去理解，而神經網絡則比較抽象，難以直觀地去理解，因為它描述的是很多數據間的復雜函數關系；第二它們對于知識的存儲方式有所不同，模糊系統通常將知識存在規則集中，而神經網絡將知識存在權系數中，但是兩者都是分布式存儲的；第三它們對于知識的運用方式不同，模糊系統計算量比較小，因為它同時激活的規則不是很多，而神經網絡計算量比較大，因為涉及到許多相關的神經元，但它們都是并行處理的；第四它們獲取知識的方式不同，模糊系統的規則并不是自動獲取的，而是由專家提供或設計，而神經網絡具有自學習的功能，無需人為設置也可以從輸入輸出樣本中自動學習權系數[16]。

鑒于以上分析，如果將兩者相結合，將更加便于解決實際應用中的相關問題。而模糊神經網絡的概念也由此產生，它將模糊系統和神經網絡相互融合，從而達到互補的效果。模糊神經網絡具有學習、聯想、識別、自適應和模糊信息處理等功能。其本質就是將常規的神經網絡輸入模糊輸入信號和模糊權值。典型的模糊神經網絡結構總共有六層。

第一層是輸入層，輸入的是精確值。x1、x2表示兩個輸入變量。第二層能夠將輸入變量模糊化，也就是隸屬函數層。

(2)

(3)

其中，m表示輸入變量x1的模糊度，n表示x2的模糊度，第二層總共有m+n個神經元；μAiμBi分別表示x1和x2的隸屬度函數。

第三層一共有m*n個節點，這些節點表示模糊規則，該層也稱“與”層。該層節點個數與第二層有關，每個節點只與第二層中前m個節點中的一個和后n個節點中的一個相連。

第四層中有q個節點，表示輸出變量模糊度劃分個數，該層也稱“或”層。該層與第三層的連接為全互連，連接權值為wkj(k=1,2,…,q;j=1,2,…,m*n)。wkj在訓練中是可以調試的，它表示每條規則的置信度。

第五層是反模糊化層，輸出的是精確值，該層與第四層的連接為全互連。

1.4 模糊小腦模型

模糊小腦模型是在上面介紹的具有認知功能的小腦模型的基礎上，加入模糊邏輯的概念，也就是將當前的輸入—理想及目標位置(PP)、理想速度和加速度(PM)模糊化，引入模糊集合的隸屬度概念，從而提高小腦模型的學習收斂速度和精度。圖2是模糊小腦模型結構圖。

2 模糊化算法

由圖2可知，模糊小腦模型包含兩種映射，分別為：R:X→M，E:M→A。

2.1 X→M映射

2.1.1 映射算法

采用的映射算法為：

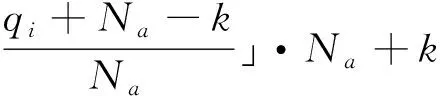
(4)

其中，qi(xi)為輸入矢量；mi,k為qi(xi)映射到中間變量M中的地址；Na為所激活單元的個數；k為激

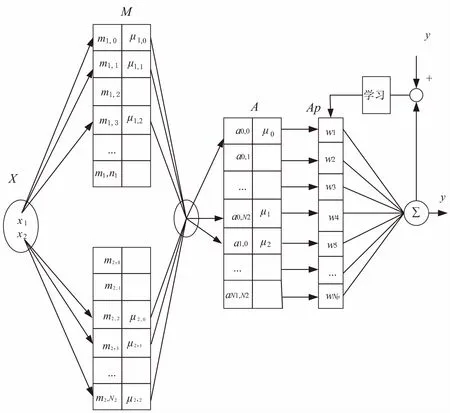
圖2 模糊小腦模型結構圖

活單元的序數，k=0～(Na-1)。

2.1.2 隸屬度函數

(1)單變量隸屬度函數。

單變量隸屬度函數定義為：

(5)

其中，σj為一個系數，可以自由選擇，對隸屬度函數圍繞中心點的寬度起到了決定性作用；而中心點就是公式中的cj，其中j表示第j個隸屬度函數；‖x-cj‖通常表示x和cj之間的距離；Ψ是一個在cj處取得最大值的函數，它是徑向對稱的，會隨著‖x-cj‖增大而快速衰減到0。對于給定的輸入x∈Rn，只有一小部分單元被激活，這些單元的中心靠近x，是由映射X→M決定。

根據以上分析，可以推算出被激活的中心點，推算公式為：

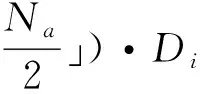
(6)

文中選用的是最常用的高斯函數：

(7)

從相鄰兩個隸屬函數的重疊可以推算出方差σj[16]：

(8)

(9)

其中，μc∈(0,1]，需要事先進行設計。

(2)多變量的隸屬度函數。

關于多維輸入向量，定義其隸屬度函數：

μ(x)=Φ(μ1,μ2,…,μn)

(10)

其中，Φ()表示相乘運算，也就是：

(11)

2.2 M→A映射

該映射可以得到M在A中所激活單元的位置，數目依然是Na。X→M映射確定后，就可以通過智能查表的方法確定X在A的位置，也就是：

ai=E(Λ,μ)

(12)

其中，Λ為張量積，其值為m1×m2×…×mn，所激活的單元表示為：

aT={a1,a2,…,aNa}

(13)

2.3 輸出映射P

輸出映射P表示為：

y=aTh(x)w

(14)

其中，aT為激活單元位置向量；x為輸入向量；h(x)為隸屬度函數矩陣，可以表示成：

(15)

根據定義，此時只需計算被激活單元的隸屬度函數值，其他數值均為0。

2.4 學習算法

首先將誤差函數定義成：

(16)

計算權重w的方法是：

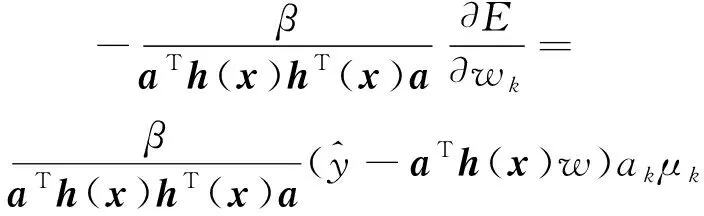
(17)

模糊小腦模型具有較強的自適應性，它可以根據所激活單元的隸屬度函數值以及這些值的平方和來確定權值的修改程度。通過對高斯函數中心點位置以及方差的學習，可以使函數逼近能力增強。高斯函數中的兩個參數可以定義為：

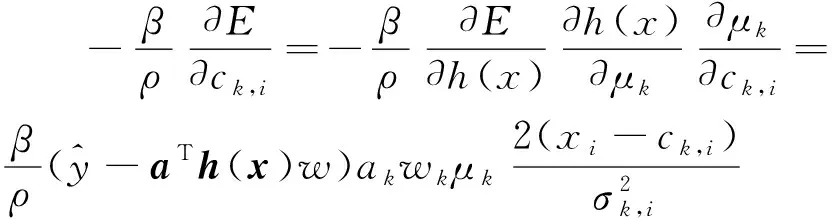
(18)

(19)

2.5 輸出導數計算

因為模糊隸屬度函數是通過感受野函數定義的，所以輸出對于輸入xi的導數可以根據上面提出的方程計算，公式的推導過程為：

(20)

3 仿真實驗

3.1 手臂模型

圖3是一個雙關節機械臂的模型，其中M表示各個關節的質量，L表示長度，g表示重心。仿真考慮了任意一個端點的質量，端點的效應力f=[fxfy]T。

表1給出了手臂模型的各種參數，其中I表示轉動慣量。

圖3 雙關節機械臂模型

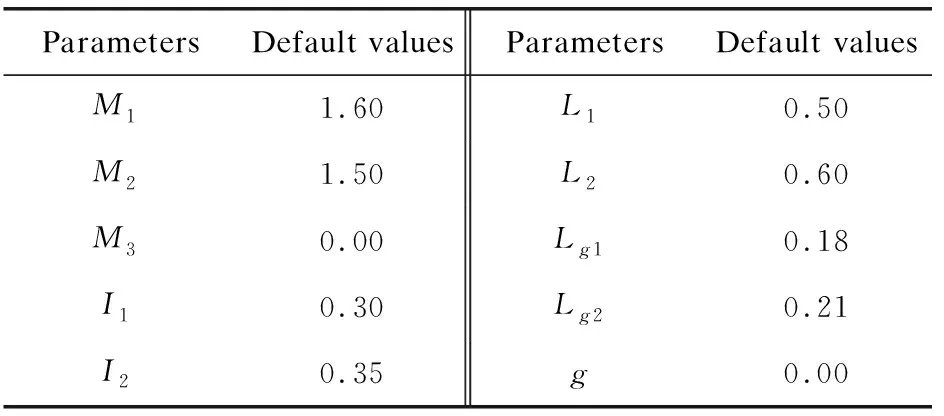
ParametersDefault valuesParametersDefault valuesM11.60L10.50M21.50L20.60M30.00Lg10.18I10.30Lg20.21I20.35g0.00

3.2 手臂控制實驗

通過Matlab實驗平臺，模糊小腦模型對機械臂做一系列測試。系統總共要做30次手臂延伸運動。實驗方法在文獻[17]中已有詳細描述，在三十次學習之后，手臂的跟蹤性能已經得到了明顯改善。圖4為學習之后的跟蹤性能圖。

圖4 學習后跟蹤性能

預定運動軌跡從中心點開始，向八個方向的目標勻速移動，圖中的細黑線為預設軌跡，粗黑線為學習三十次之后的跟蹤軌跡。從圖中可以看出，在多次學習之后，模型的跟蹤性能得到了顯著提高，此時與理想軌跡的誤差已經很小了。由此可見，該模型能夠像小腦模型一樣實現對手臂的控制。

為了比較該模型和小腦模型的性能差異，對小腦模型也進行相同的實驗，將兩者的跟蹤誤差進行比較，如圖5所示。

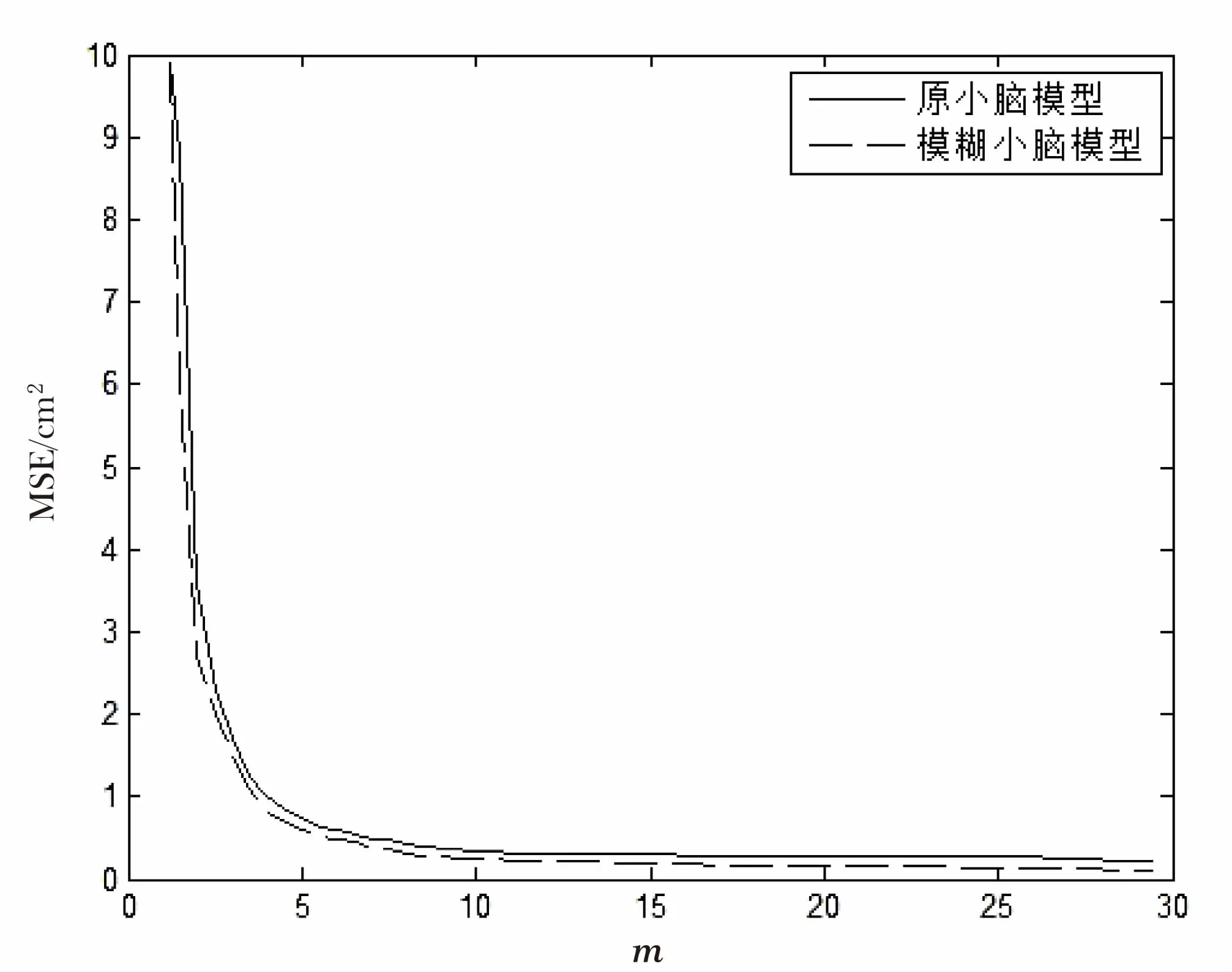
圖5 學習實驗跟蹤誤差

由圖5可知，通過在認知小腦模型的輸入部分引入模糊集合的隸屬度概念，能夠在幾次學習之后產生精確的軌跡，而且與原模型相比具有更高的控制精度。

4 結束語

文中對認知小腦模型的研究另辟蹊徑，將注意力集中于小腦模型的輸入部分，引入模糊集合的概念。通過對認知型小腦模型和模糊理論的簡單介紹，說明了兩者結合的可能性，提出模糊小腦模型的想法。最后，將新模型與原模型對于手臂的控制誤差進行對比，有效地說明了模糊小腦模型能夠提高控制精度。

但是該模型還存在一些不足，比如在考慮提高小腦模型精度的同時并沒有過多考慮各種擾動的問題，當存在擾動時，該模型在精度方面是否依然優于原模型還有待研究。