應用型本科院校《數字信號處理》教學探討

福建師范大學福清分校電子與信息工程學院 張賽男

引言

數字信號處理是電子信息類專業的一門重要專業基礎課。該課程從時域和變換域的角度利用Z變換、傅立葉變換等數學方法，分析離散時間信號與系統的特性；通過對IIR濾波器和FIR濾波器的設計，分析了數字信號處理的實現方法。在常規教學模式下，各種數字信號處理的理論大都滿是數學推導，看起來像數學分析課程一樣，學生感覺很枯燥無味，缺乏學習興趣。最后學生雖然通過了考試，卻存在這樣的矛盾現象：一方面數字信號處理很有用，另一方面學了數字信號處理不會用。

應用型本科院校的人才培訓目標是造就工業化象信息化時代轉型和發展過程中各行各業急需的各類應用型、行業特色型人才。為適應這一人才培養目標，應用型本科院校需要建立應用型、實踐型課程體系。特別是對于數字信號處理這樣一門理論性很強的專業基礎課來說，轉變原有的教學理念，建立適應應用型本科院校人才培養目標的教學內容和方法顯得尤為重要。

一般的實驗箱學生也只是機械的連線，記錄波形，并不懂的分析過程。Matlab是數字信號處理的一個卓越平臺，具有開放的環境、功能極強的矩陣運算、圖形繪制、數據處理、各種工具箱等許多優點。利用Matlab對數字信號處理的理論應用于實踐設計，通過這樣把枯燥難學的課程變得有趣，有效的提高教學質量。

1 教學方法的探討

結合應用型本科院校的人才培養目標于數字信號處理課程理論性強的特點，本文提出一種新的教學模式。從實際工程問題出發，學生在老師的指導下，分析并設計解決方案，在計算機上利用matlab進行仿真驗證，教師引導學生歸納，總結解決問題的方法，從而提出數字信號處理中的知識點，利用剛得到的知識點再回頭到實際問題的解決中，進一步升華對知識點的靈活應用能力。

在教學中先給學生提出一個實際需要解決的問題，激發學生的學習興趣和解決問題的好奇心。傳統教學模式是先給出一個定義或定理，然后證明推理，介紹相關的性質，學生聽起來感覺很枯燥無味。這種先提出問題的方式，讓學生明白任何理論知識都是從實際出發，知道相關理論知識的應用背景。針對數字信號處理的重要知識點，問題的提出要精心設計，有助于喚起學生的興趣和積極思維。

針對上面提出的實際問題，在老師指導下學生自己嘗試動手解決問題，在分析問題中發現并歸納整理所得結論。這點符合應用型本科院校的人才培養目標。老師給學生提出討論和實驗要求，學生按照要求以個人、小組或者班級體進行討論，在計算機上利用Matlab軟件分析解決經過簡化的實際問題，完成相應的實驗，對得到的相關數據做整理，分析歸納對實驗結果描述出來。對結果圖形繪制出來更直觀形象的理解。根據現有的結論，去猜想更為一般的結論。這樣就得到了數字信號處理中的知識點。

老師通過對數字信號處理中的知識點進行講解，讓學生從理論上把握該知識點。這和傳統教學中對知識點的理論推導證明不同。采用板書與多媒體相結合的教學模式。在授課過程中，對于復雜的公式推導、例題講解可以采用板書的授課方式，這樣在老師推導板書的過程中，學生有足夠的時間思考，跟上老師的講課思路，加深印象；對于抽象的理論和一些難于理解的問題可以采用多媒體的授課方式，把抽象的概念形象化，增加一些動畫演示來幫助學生理解，這樣既直觀又形象。

在應用型本科教育背景下，應強調知識點是什么背景下產生的，它的主要應用有哪些方面，如何應用。詳細的理論推導可以淡化，有興趣的同學可以自己課下看。老師要用簡單易懂的語言去描述抽樣的數字信號處理知識點，通過簡單的動畫演示讓學生更好的理解知識點。根據知識點再進一步和相關領域中的應用結合。

2 案例分析

在數字信號處理關于離散時間系統的變換域分析，按照傳統的教學方法會對系統函數、離散時間系統的Z變換解法、系統函數的零極點和頻域響應等知識點進行講解，最后給出幾個像數學一樣的題目。學生覺得太麻煩太抽樣不易理解，更談不上現實中哪些方面會靈活應用到這些知識。這和應用型本科院校的人才培養目標不一致。按照上述教學模型，離散時間系統的變換域分析這一節內容的教學分為以下幾部分。

2.1 應用情景

聲音在傳播過程中遇到障礙物會發生反射，反射過來的聲音即回聲。回聲和直接聲相比時間上會有延遲，幅度會衰減。聲波在房間中被隨機多次發射便會有一系列的延時和衰減，最終聽到的聲音就是混響效果。混響是一種常見的音頻特效處理算法，應用很廣泛。比如音樂廳、劇場等音樂演奏的空間，需要混響效果使樂曲更加舒緩而愉悅；教室、錄音室等語言使用的空間，需要減少混響使講話更清晰。

較簡單的電子混響器采用逐級移位延遲線，將信號延遲一定時間，然后將此信號與原信號以適當的比例混合，產生混響效果。延遲時間取決于移位時鐘脈沖的頻率以及移位的級數。在移位脈沖的控制下，此數字信號逐級移位，控制移位脈沖的頻率以及移位寄存器的長度，可在移位寄存器的輸出端得到延遲時間不同的信號。改變信號的延遲時間幅度及其幅度，并將與原信號混合，即可獲得不同的混響效果。

2.2 給出抽象的數學模型

圖1是一個簡單混響系統的實現框圖。

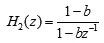
b為低通濾波器的極點。

根據框圖學生自己寫出系統函數為：

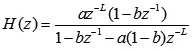
給出具體參數如a=0.83,b=0.08,L=10，要求學生用matlab分析該混響系統零極點如何分布？其單位沖擊響應怎么樣？頻域響應又有什么特點？

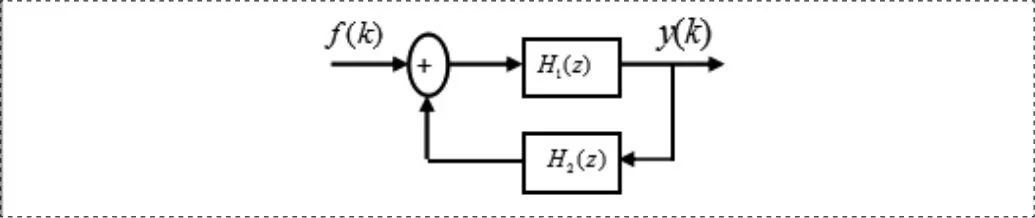
圖1 簡單混響系統框圖

2.3 Matlab仿真

matlab代碼在老師的指導下完成，得出圖2到圖5四個圖形，并分析特點。

圖2是零極點圖，混響系統的極點非常靠近單位圓，均勻分布在半徑小于1的圓上。極點全部在單位圓內，該系統是個穩定系統。圖3是單位沖激響應，隨著時間的增大逐步衰減。

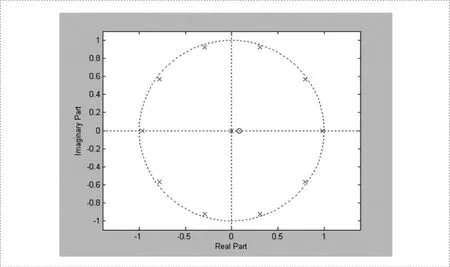
圖2 零極點圖

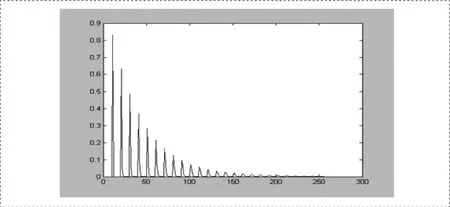
圖3 單位沖激響應

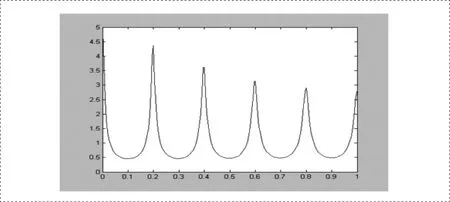
圖4 幅頻響應

圖4是幅頻響應，只給出半個周期部分，連續的，每個極點處均有一個峰值，形狀像把梳子。極點處的峰值隨著頻率的增減逐步減小。圖5是相頻響應，只給出半個周期部分，連續的，相位不是線性的。

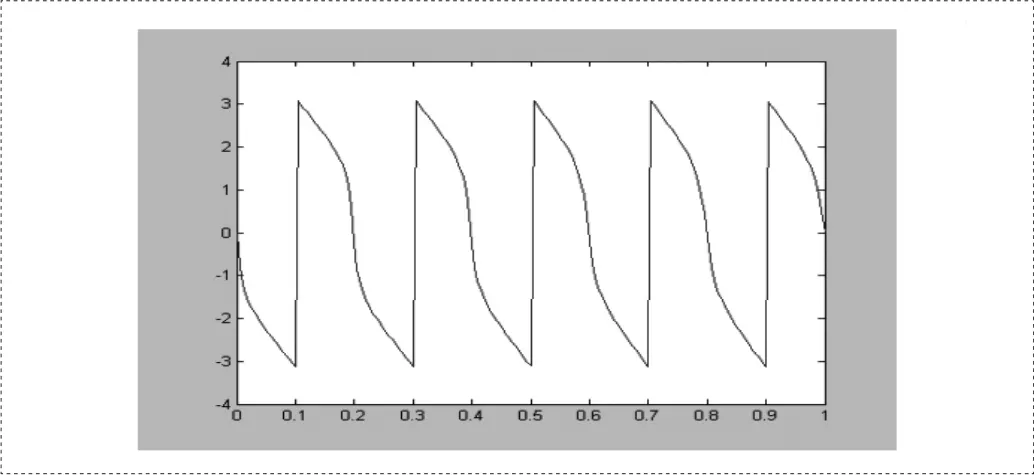
圖5 相頻響應

2.4 歸納知識點

根據上述的實驗結論，我們可以歸納出一般離散時間系統變換域分析的特點。零極點圖不僅可以看出單位沖激響應的衰減放大關系，還能看出系統的因果性和穩定性。如系統穩定的充要條件：系統函數H(z)的所有極點都必須在單位圓內。由幅頻特性可知：當頻率點變到極點附近時，就會在該極點附近的頻率出現峰值，極點越接近單位圓，峰值就越尖銳；同樣，當頻率點變到零點附近時，就會在該零點附近的頻率出現低谷，當零點在單位圓上時，該零點就是傳輸零點。可見在單位圓附近的零極點對系統的幅頻特性有較大的影響。零點可在單位圓內外，但極點只能在單位圓內，否則系統將不穩定。而系統的相位響應對幅度特性沒有影響。相頻響應反映了系統對不同頻率信號的處理時間。

2.5 回歸教材和應用

針對以上知識點，對教材內容做串講，主要從向量角度進行講解，讓學生換個角度來理解知識點。根據不同章節知識特點，這一部分會有對應形象而直觀的動畫演示。最后以人的聽覺系統和視覺系統對幅度失真和相位失真的不同敏感度，列舉相位頻譜和幅度頻譜對合成出圖像造成影響程度的一些直觀例子，讓同學思考其他方面具體的應用。

3 結束語

數字信號處理這門課程在電子通信專業占有非常重要的地位，將matlab引入數字信號處理的教學中，從實踐中出發，到理論研究，再到實踐中去，使學生擺脫了一般數字信號處理知識的枯燥與乏味，對這門課有個更全面的認識。這也符合應用型本科院校的學生應更注重實踐教學的特點，通過實踐可以達到對理論知識的復習和鞏固的效果，同時學生能夠更直觀地領會和理解本課程的分析、設計方法和處理結果，感受數字信號處理在科學研究與實際工作、生活中的重要意義，提高教學質量。