基于最速下降法的可展開索網天線型面調整方法

，,*，

1. 同濟大學 建筑工程系，上海 200092 2. 上海躍盛信息技術有限公司，上海 200240

無線通信、全球衛星導航、高分辨率對地觀測、電子偵察及深空探測等領域對星載天線提出了多功能、多頻段的要求。星載天線正趨于高精度、大型化發展。隨著新型航天材料的研制、設計理念和研究方法的更新,以及試驗技術的提高，可展天線在過去20年得到迅速發展[1-5]。索網天線作為空間可展開天線的一種重要結構形式，合理地協調了精度與口徑的兼容性問題，具有高度的研發需求和應用價值。根據支撐結構與展開驅動方式的不同，索網天線主要包括傘形天線、環形桁架天線、模塊化構架天線等結構方案[6-8]。理論上，索網天線口徑最大可達50 m，型面精度最高可達0.2 mm[3]。

預應力索網結構是索網天線反射面成型與精度保持的關鍵技術[9-10]。以最具代表性的環形桁架天線AstroMesh[7]為例，其雙層索網結構由前索網、背索網和張力陣三部分組成。雙層索網結構的內部節點通過縱向張力陣連接，邊界節點與環形桁架的“硬點”連接。通常，背索網與前索網幾何對稱，以保證雙層索網結構具有良好的熱穩定性。國內外研究工作主要針對索網結構的拓撲設計、預應力優化、熱穩定性分析等內容，已有較成熟的研究方法和大量的研究成果[11-15]。

此外，由于環境因素(重力)和各種誤差因素(制造、裝配等)的影響，索網天線必然存在初始型面誤差[16-17]。工程上，需要采用相應的試驗手段和調整技術以降低上述不利因素引起的初始型面誤差[18-19]。在索網天線地面試驗中，對于不可消除的重力，需要設計一套合理的重力卸載裝置與卸載方案。對于制造與裝配誤差，傳統的調整方法主要依靠人工，經過反復的型面幾何測量和張力陣彈簧拉力調整迭代過程，直至初始型面誤差滿足要求。索網結構具有強烈的幾何非線性，調整過程中索網節點位移之間高度耦合。隨著索網結構單元與節點數量增多，傳統調整方法目的性差、效率低等缺點體現得尤為明顯。對此，一些學者提出基于數值優化技術的索網結構型面調整算法，例如將遺傳算法[20]、序列二次規劃法[21]和進退法[22]與索網結構非線性有限元模型相結合的型面調整方法。

本文從雙層索網結構的拓撲關系和平衡方程出發，利用偏導方法推導出型面誤差對張力陣拉力的梯度公式，確定任意平衡狀態下對型面精度影響最顯著的張力陣單元，結合最速下降法，提出一種快速、有效的型面調整方法，為實際工程提供理論依據。

1 分析方法

1.1 型面誤差梯度公式

索網結構的型面調整過程，可以看作是索網從含有誤差的初始幾何逐漸向目標反射面逼近的一系列變形過程。對于雙層索網結構，最直接的調整對象為張力陣彈簧，即通過改變彈簧拉力使前索網節點位于目標反射面上。因此，首先推導型面誤差對張力陣彈簧拉力的梯度公式，為確定型面調整的優化路徑提供理論依據。推導過程如下：

在任意的平衡狀態下，雙層索網結構幾何為：

式中：xf為前索網(front net)節點坐標；xr為背索網(rear net)節點坐標。

雙層索網結構的張力為：

式中：tf為前索網索單元拉力；tr為背索網索單元拉力；tt為張力陣(tension tie)彈簧拉力。

雙層索網結構的節點外力為：

式中：pf為前索網節點外力；pr為背索網節點外力。

雙層索網結構的節點位移為：

式中：uf為前索網節點位移；ur為背索網節點位移。

根據雙層索網結構的拓撲關系，將全部前索網、背索網索單元及張力陣彈簧單元的方向向量組裝成平衡聯結矩陣C，并分塊表示為：

雙層索網結構張力與節點外力的平衡關系可寫作：

(1)

或簡記作：

Ct=p

將雙層索網結構的柔度矩陣D分塊表示為：

雙層索網結構的平衡方程可寫作：

(2)

或簡記作：

u=Dp

假設目標反射面的幾何方程為：

(3)

式中：f為拋物面焦距。

型面誤差δrms為前索網節點坐標的函數：

(4)

式中：Δxf為前索網節點相對于目標拋物面的幾何偏差;N為前索網節點數。

型面誤差δrms對彈簧拉力tt的偏導可表示為：

(5)

首先，考慮式(5)右邊第一項，即型面誤差對前索網節點坐標的偏導。對于前索網的某個節點xf,k(xf,k,yf,k,zf,k)，取其沿焦軸方向到拋物面的距離作為該節點誤差，即

結合式(4)，推導得到型面誤差對前索網節點坐標的偏導表達式為：

其中，

然后，考慮式(5)右邊第二項，即前索網節點坐標對節點外力的偏導。在數值優化算法中，若通過控制優化步長，使相鄰優化步之間的雙層索網結構滿足小變形假設，則某一步優化中前索網節點坐標對節點外力的偏導可由前一步優化所發生的前索網節點位移對節點外力的偏導代替，即

(6)

結合式(2)，式(6)可寫作:

(7)

最后，考慮式(5)右邊第三項，即節點外力對彈簧拉力的偏導。結合式(1)，該項可寫作：

(8)

綜上，將式(7)、(8)代入式(5)，得到型面誤差梯度的顯性表達式為：

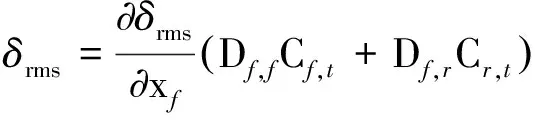
(9)

由式(9)計算得到型面誤差梯度的無窮范數‖▽δrms(tt)‖∞，可確定該平衡狀態下對型面精度影響最顯著的張力陣彈簧單元，選其作為型面調整的控制變量，結合最優化算法，快速降低型面誤差。

1.2 型面精度調整方法

考慮雙層索網結構中索段長度誤差對型面精度的影響，采用最速下降法(即梯度法)進行型面調整。目標函數為型面誤差δrms，優化變量為張力陣彈簧拉力tt，選擇型面誤差值下降最快的方向(即負梯度方向)作為搜索方向，具體步驟如下：

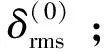
2)指定優化精度ε>0，在第k步優化中，由式(8)計算型面誤差梯度向量的模量|▽δrms(tt)(k)|并判斷精度：如果|▽δrms(tt)(k)|>ε，則選擇(tt)(k)處的負梯度方向，即-▽δrms(tt)(k)作為優化搜索方向；如果|▽δrms(tt)(k)|<ε，則停止計算，輸出(tt)(k)作為調整后的彈簧拉力；

3)第k步優化步長λ(k)的計算公式為：

式中：α為步長調整因子；Δt為彈簧拉力的單位調整量。

4)令(tt)(k+1)=(tt)(k)-λ(k)▽δrms(tt)(k)，重復步驟2)～3)。

利用Fortran計算機語言編程實現上述基于最速下降法的型面調整方法。

2 雙層索網分析模型

建立一個5 m口徑環形桁架天線的雙層索網模型，如圖1所示。前索網、背索網均采用三向網格形式，二者幾何對稱，索段平均長度約為500 mm。索網邊界節點與環形桁架硬點連接，內部節點通過張力陣連接。前索網節點均位于目標拋物面，拋物面焦距為3.0 m。張力陣構件由三段單元串聯組成，即中間拉伸段和上、下連接段。拉伸段為線性彈簧，連接段彈性剛度遠大于彈簧拉伸剛度。前索網和背索網索段的彈性模量為20 GPa，截面積為1.0 mm2。線性彈簧的拉伸剛度為1.0 N/mm。

圖1 環形桁架天線雙層索網結構Fig.1 Double-layer cable-net structure of the ring truss antenna

在雙層索網結構的數值模型中，前索網和背索網索單元、張力陣彈簧和連接段均為只能承受軸向拉力的兩節點單元。對于幾何確定的雙層索網結構，不考慮結構自重及邊界桁架的彈性變形，指定所有的張力陣彈簧拉力為6.0 N，通過找力分析得到設計狀態下雙層索網結構預張力。前索網預張力分布如圖2所示，內部索單元預張力分布均勻，最小值為18.71 N，最大值為26.78 N，邊界索單元預張力最大值為38.69 N。由于結構對稱性，背索網預張力結果與前索網相同。

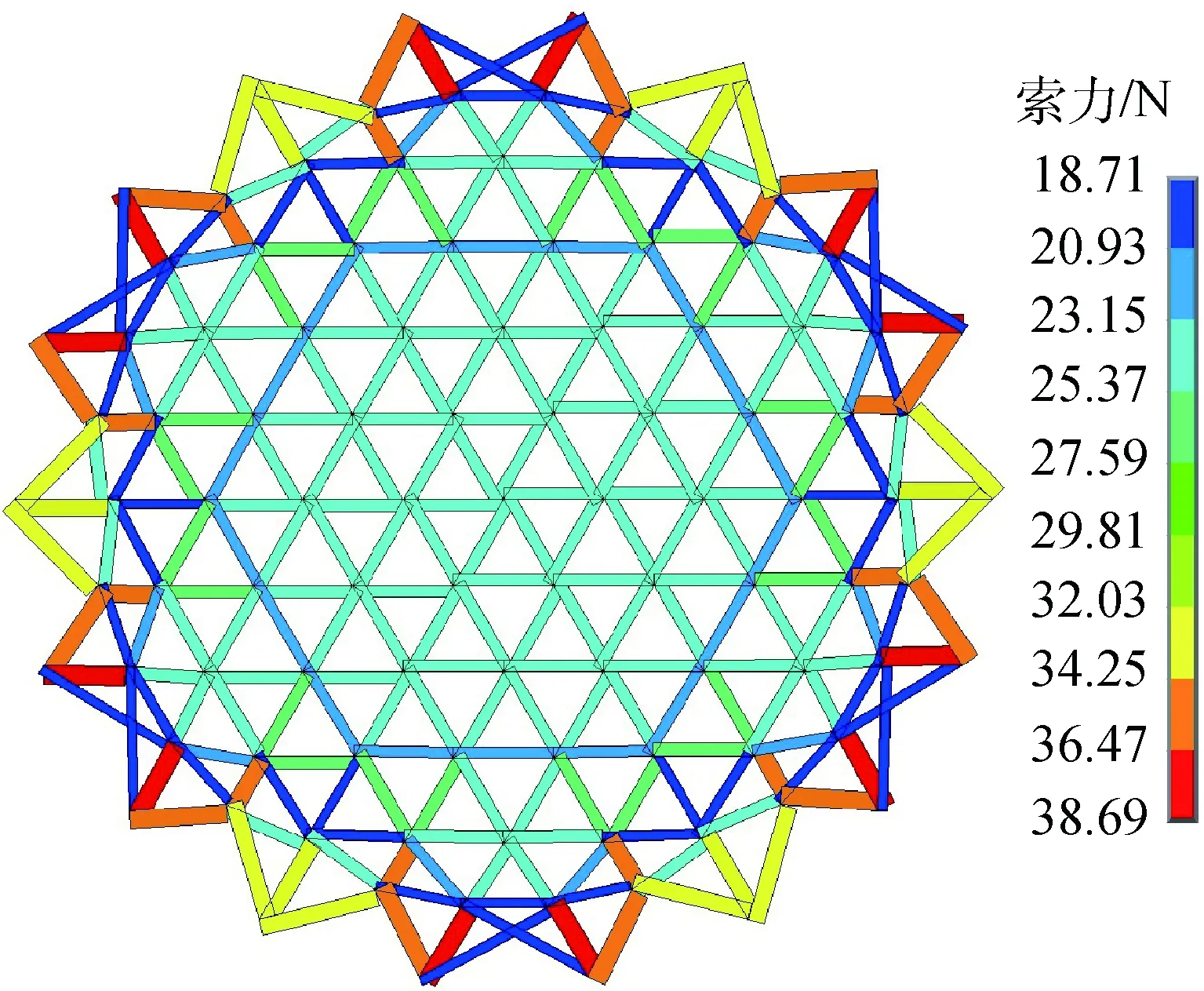
圖2 設計狀態下前索網預張力分布Fig.2 Pre-tension distribution of the front cable-net in the design state

3 型面調整算例

針對圖1所示的雙層索網模型，通過數值試驗驗證本文所提出型面調整方法的有效性。雙層索網模型中索段長度誤差為獨立的隨機數，假設其滿足標準正態分布N(0,σ2)。進行4組數值試驗，分別指定索段長度誤差的標準差為0.05 mm(試驗1)、0.10 mm(試驗2)、0.15 mm(試驗3)、0.20 mm(試驗4)，依次將索段長度誤差引入設計狀態的雙層索網模型，靜力分析，得到初始的誤差平衡狀態，利用程序進行型面調整優化計算，分析調整過程中型面誤差變化情況和雙層索網模型預張力分布情況。此外，假設彈簧拉力的單位調整量Δt為0.10 N，為滿足式(7)成立的小變形假設，調整因子α取為0.50。

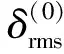
圖3 型面調整過程型面誤差Fig.3 Surface error in the surface adjustment process

調整前、后雙層索網模型的彈簧拉力值分布如圖4所示。設計狀態下張力陣彈簧拉力均為6.0 N。考慮型面調整前的初始狀態，由于索段長度誤差的存在，彈簧拉力會變得不均勻。對比4組試驗可以發現，隨著索段長度誤差的增大，彈簧拉力的不均勻程度增加。在同一組試驗內，調整后的彈簧拉力最小值變得更小、最大值變得更大，彈簧拉力不均勻程度有進一步增加趨勢。

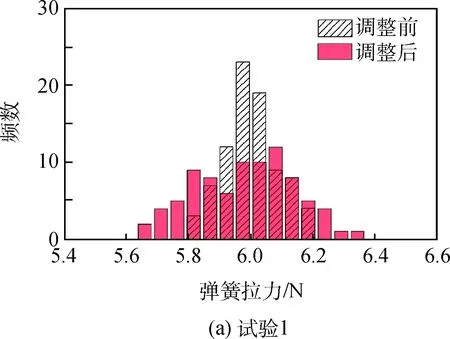
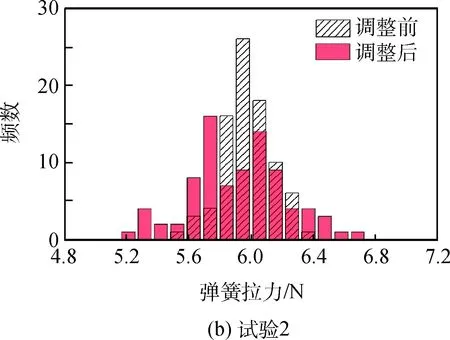
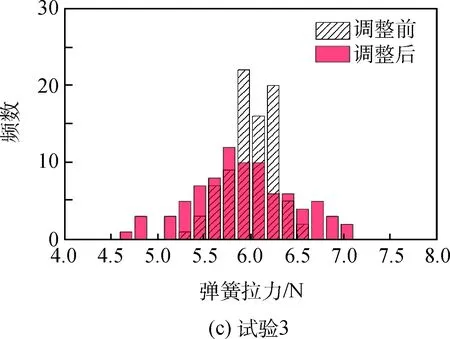
圖4 型面調整前、后彈簧拉力分布Fig.4 Spring tensions before and after the surface adjustment

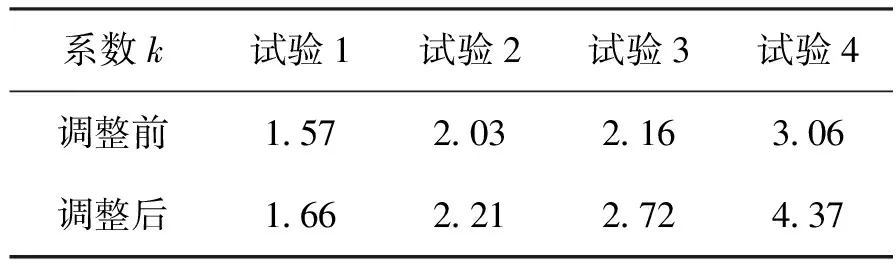
表1 型面調整前、后前索網預張力系數

一方面，從誤差來源角度講，需提高索網制造與裝配工藝，降低由索網長度誤差引起的型面誤差。另一方面，可以改進基于最速下降法的型面調整方法，例如引入適當的約束條件，使調整后的雙層索網模型預張力分布滿足工程要求。

4 結束語

本文針對空間可展天線的雙層索網結構，基于拓撲關系和平衡方程，利用偏導方法推導了任意平衡狀態下型面誤差對張力陣拉力的梯度公式。公式具有一般性，適用于不同形式的雙層索網結構型面調整。結論與展望如下：

1)根據型面誤差梯度向量的無窮范數，可以確定對型面誤差影響最顯著的張力陣單元；

2)基于最速下降法的雙層索網結構型面調整方法是有效的，采用型面誤差負梯度方向作為優化搜索路徑，可實現快速降低型面誤差的目的；

3)在后續研究中，考慮引入適當的約束條件，提高型面調整后雙層索網結構的預張力均勻程度。