半球面氣體軸承穩態承載力分析

賈晨輝，高靖，邱明，馬文鎖

（河南科技大學 機電工程學院，河南 洛陽 471003）

隨著科技的發展，高轉速機械已成為高效率生產的工具，氣體軸承在許多應用領域可以提高機械的工作效率。氣體軸承支承的轉子轉速高、無噪聲且摩擦小，顯現出許多傳統軸承沒有的優點[1]，在微細工程、醫療機械和空間技術等領域得到極大應用。

采用小孔節流的半球面螺旋槽動靜壓氣體軸承具有新型結構。其綜合了靜壓與動壓軸承的優點，即在轉子啟停階段使用靜壓氣體軸承的供氣方式，形成靜壓承載能力，避免了干摩擦；在轉子高速旋轉時利用螺旋槽產生強的動壓效應，形成動壓承載能力，避免了支承軸承所需的持續高壓供氣[2-3]，較同類軸承有較高承載力。

現建立供氣切向角可變的半球面動靜壓氣體軸承潤滑分析數學模型，采用有限差分法[4]求解，并通過編程數值計算氣膜的穩態壓力分布，求解氣膜的穩態承載力，研究不同軸承參數（節流孔數和分布、供氣壓力、供氣切向角）對軸承穩態承載力的影響規律。

1 半球面氣體軸承結構

半球面螺旋槽動靜壓氣體軸承的結構如圖1所示。圖中，β為螺旋角；ω為軸頸轉速；φ為供氣切向角；α0為轉子小端角度；α1為螺旋槽起始端角度；α2為轉子大端角度；ps為小孔供氣壓力；br為臺寬；bg為槽寬；hg為槽區間隙；h0為臺域內氣膜平均間隙。軸承由定子和轉子組成，節流孔加工在定子上，轉子上加工有螺旋槽，節流孔位置與螺旋槽分布沒有相互影響。

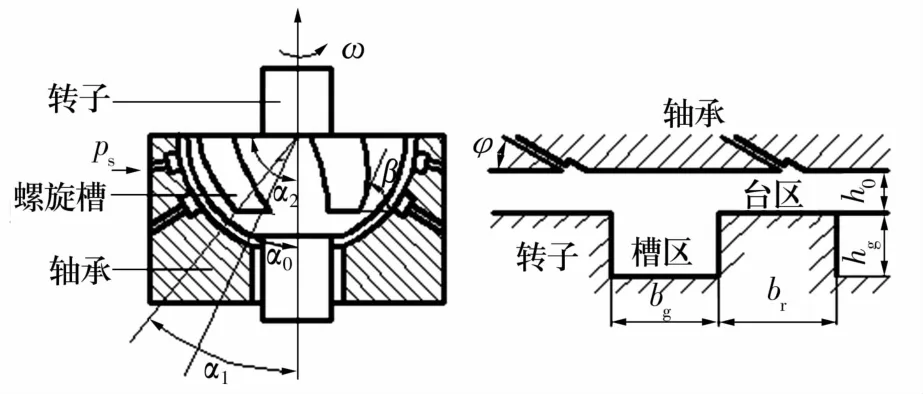
圖1 半球面螺旋槽動靜壓氣體軸承剖面示意圖Fig.1 Schematic diagram of semispherical spiral groove hybrid gas bearing

2 半球面氣體軸承潤滑分析數學模型

球面坐標系如圖2所示。以氣體潤滑運動方程、連續性方程、狀態方程和節流孔流量方程[5-8]為基礎，結合Newton黏性定律和Reynolds方程假設，在球面坐標系下推導供氣切向角可變的半球面動靜壓氣體軸承非線性量綱一的Reynolds方程[5]。

圖2 球面坐標系Fig.2 Spherical coordinate

圖2中旋轉面上任意一點M可用?，α和r表示。圖中，?為周向坐標；α為沿旋轉素線的子午線方向坐標；r為點M與旋轉中心連線的距離。

3 軸承穩態承載力的求解

3.1 數值計算穩態壓力

由于軸承的穩態Reynolds方程與時間項無關，故簡化得到穩態潤滑分析量綱一的Reynolds方程為

在廣義坐標系下采用有限差分法對（8）式離散化，推導出穩態壓力的差分表達式。為了計算的方便和精確，在斜坐標系 （x＝?＋ξ／tanβ，y＝-ξ／sinβ）下劃分網格，周向網格數為500（根據計算調整設定），徑向網格數為90，周向步長為0.012 56，徑向步長為0.019 23，劃分時周向槽臺邊界線到原點之間網格數設定為50（根據計算調整設定），使這段邊界線正好在網格點上，徑向槽臺邊界線在計算時對網格數取整，使邊界線落在網格線上，這樣網格線就落在槽臺交界線上[10]，如圖3所示。由于求解域內氣膜厚度不連續，在求解Reynolds方程時分為連續（包括小孔區域）和不連續情況。

圖3 求解域網格劃分示意圖Fig.3 Diagram of meshing for solution domain

以求解小孔區域為例，對（8）式等號兩側在每個網格節點的平行四邊形求解域abcd（記作Di，j，圖4）上進行面積分得

圖4 氣膜厚度連續區域的網格Fig.4 Continuous regional grid of gas film thickness

氣體軸承設計參數見表1，采用表1進行編程數值計算。

表1 氣體軸承設計參數Tab.1 Design parameters for gas bearing

在供氣壓力 ps＝0．3 MPa、轉速 n＝20 000 r／min以及表1設計參數情況下，軸承量綱一的氣膜厚度和壓力分布分別如圖5和圖6所示，橫縱坐標分別代表量綱一的周向長度與徑向長度的網格數。由圖5可知，由于軸承表面存在螺旋槽，氣膜厚度在周向和徑向上不連續，在槽臺交界處存在氣膜厚度突變；由圖6可知，氣膜壓力隨著氣膜厚度的增大而減小，總體分布趨勢是沿周向先由大變小，再由小變大，在小孔區域存在壓力突變，槽臺交界處壓力最大。

圖5 量綱一的氣膜厚度的三維分布Fig.5 3D distribution of dimensionless gas film thickness

圖6 量綱一的氣膜壓力的三維分布Fig.6 3D distribution of dimensionless gas film pressure

3.2 數值計算軸承穩態承載力

計算流程圖如圖7所示。

圖7 軸承承載力計算流程圖Fig.7 Flow chart for calculation of load capacity of bearing

4 軸承參數對承載力的影響規律

4.1 不同轉速下節流孔數、供氣壓力、供氣切向角對軸承承載力的影響

不同轉速下節流孔數、供氣壓力、供氣切向角對軸承承載力的影響如圖8—圖10所示。

圖8 不同轉速下節流孔數對軸承承載力的影響Fig.8 Influence of numbers of orifices on load capacity of bearing under different rotational speeds

圖9 不同轉速下供氣壓力對軸承承載力的影響Fig.9 Influence of gas supply pressure on load capacity of bearing under different rotational speeds

圖10 不同轉速下供氣切向角對軸承承載力的影響Fig.10 Influence of gas supply tangential angle on load capacity of bearing under different rotational speeds

由圖8可知，軸承承載力隨著轉速和節流孔數的增加而增大，轉速越大，節流孔數對承載力的影響越弱。基于承載性能考慮，應選擇節流孔數s＝12（雙排）的軸承。由圖9可知，隨著供氣壓力增加，靜壓效應增強，軸承承載力增大；隨著轉速逐漸增加，供氣壓力對軸承承載力的影響減弱。基于對承載性能與實際供氣要求的考慮，應選擇ps＝0．5 MPa。由圖10可知，隨著轉速增加，軸承承載力增大；隨著供氣切向角增加，軸承承載力先減小后增大；轉速越大，供氣切向角對軸承承載力的影響越弱。基于承載性能考慮，供氣切向角應避免選擇40°～60°。

4.2 不同偏心率下節流孔數、供氣切向角對軸承載力的影響

不同偏心率下節流孔數、供氣切向角對軸承承載力的影響如圖11、圖12所示。

圖11 不同偏心率下節流孔數對軸承承載力的影響Fig.11 Influence of numbers of orifices on load capacity of bearing under different eccentricities

圖12 不同偏心率下供氣切向角對軸承承載力的影響Fig.12 Influence of gas supply tangential angle on load capacity of bearing under different eccentricities

由圖11可知，軸承承載力隨著偏心率和節流孔數的增加而增大，偏心率越大，節流孔數對承載力的影響越強。基于承載性能考慮，應選擇節流孔數s＝12（雙排）的軸承。由圖12可知，隨著偏心率增加，軸承承載力增大；隨著供氣切向角增加，軸承承載力先減小后增大；偏心率越大，供氣切向角對軸承承載力的影響越強。基于承載性能考慮，供氣切向角應避免選擇40°～60°。

4.3 節流孔分布對軸承承載力的影響

不同節流孔分布位置的軸承承載力見表2。節流孔沿軸承的分布位置不同，得到的軸承承載力也不同，節流孔沿軸承子午線方向均勻分布在螺旋槽區域的承載力大于均勻分布在其他區域的承載力。基于承載性能考慮，應將節流孔均勻分布在螺旋槽區域。

表2 不同節流孔分布位置的軸承承載力Tab.2 Dimensionless load capacity of bearing with different distribution locations of orifices

4.4 小結

綜上，基于承載性能考慮，應選擇節流孔數s＝12（雙排）的軸承，節流孔均勻分布在螺旋槽區域，供氣壓力ps＝0.5 MPa，且供氣切向角應避開40°～60°。

5 結論

1）采用有限差分法求解控制方程，有利于編程計算求解軸承氣膜壓力分布。對半球面螺旋槽動靜壓氣體軸承的求解方法普遍適用于求解其他結構的動靜壓氣體軸承的控制方程。

2）軸承承載力隨著轉速、偏心率與節流孔數的增加而增加；轉速越大，節流孔數對承載力的影響越弱；偏心率越大，節流孔數對承載力的影響越強。

3）節流孔沿軸承的分布位置不同，承載力也不同；節流孔沿軸承子午線方向均勻分布在螺旋槽區域的承載力大于均勻分布在其他區域的承載力。

4）隨著供氣壓力增加，承載力增大；隨著轉速逐漸增加，供氣壓力對承載力的影響減弱。隨著轉速、偏心率的增加，承載力增大；隨著供氣切向角增加，承載力先減小后增大；轉速越大，供氣切向角對軸承承載力的影響減弱；偏心率越大，供氣切向角對軸承承載力的影響越強。

5）基于承載性能考慮，應選擇節流孔數s＝12（雙排）的軸承，節流孔均勻分布在螺旋槽區域，供氣壓力ps＝0.5 MPa，且供氣切向角應避開40°～60°。