矩陣機制下差分隱私數(shù)據(jù)發(fā)布方法的誤差分析*

吳英杰，陳靖麟，蔡劍平，王一蕾

福州大學 數(shù)學與計算機科學學院，福州 350108

1 引言

在現(xiàn)實生活中，由于數(shù)據(jù)統(tǒng)計和科學研究的需要，許多研究機構(gòu)或組織都會對外發(fā)布數(shù)據(jù)。如何保證所發(fā)布的數(shù)據(jù)既是可用的，又不會泄漏數(shù)據(jù)中所包含的個體的隱私信息，已成為當前數(shù)據(jù)挖掘與信息共享領域一個十分熱門的研究課題。針對此類問題，國際上眾多研究人員對隱私保護數(shù)據(jù)發(fā)布進行了深入研究，提出了不少隱私保護數(shù)據(jù)發(fā)布模型。然而，現(xiàn)有的隱私保護模型大多以匿名為基礎，這些模型均需要特殊的攻擊假設和一定的背景知識，因此具有很大的局限性。為此，Dwork等人[1-3]提出了差分隱私模型，該模型適用于各種背景條件，并且具有嚴格的數(shù)學證明，得到了廣泛的認可。基于該隱私保護模型，學者們開展了很多相關研究工作，內(nèi)容涉及直方圖發(fā)布[4-8]、連續(xù)數(shù)據(jù)發(fā)布[9]、空間劃分發(fā)布[10-11]、智能數(shù)據(jù)分析[12-14]等。

差分隱私算法通過對數(shù)據(jù)添加隨機噪聲來實現(xiàn)隱私保護，因此在保護隱私的同時必然會產(chǎn)生相應的數(shù)據(jù)誤差。算法的誤差是評價算法的重要指標，因此對于差分隱私算法來說，計算均方誤差是該算法最為基本也是最為重要的工作。然而，現(xiàn)有的大部分差分隱私算法對均方誤差的估計，往往是基于實驗或者采用先統(tǒng)計各變量的均方誤差再累加的方法。該做法使得難以對算法的均方誤差進行定量分析，或者使得分析過程極為復雜，不能有效、簡潔地讓讀者了解該算法的精確性，給讀者在算法的理解上造成一定的困擾。

近年來，許多研究學者提出了多種差分隱私數(shù)據(jù)發(fā)布算法，其中多數(shù)集中在兩方面：一是以k-叉樹的形式對數(shù)據(jù)進行處理，然后采用一致性約束的分層結(jié)構(gòu)差分隱私算法；二是利用策略矩陣進行變換，加噪后通過還原矩陣進行還原的基于矩陣機制的差分隱私算法。其中，Qardaji等人[15]對以Boost為代表的分層結(jié)構(gòu)差分隱私算法的均方誤差進行了有效的理論分析，并提出相應的求解方法。而以Prievlet算法為代表的基于矩陣機制的差分隱私算法尚缺乏相應的理論分析，本文通過研究現(xiàn)有的差分隱私數(shù)據(jù)發(fā)布算法對均方誤差的計算，并結(jié)合矩陣運算的相關理論，提出基于矩陣運算的均方誤差計算方法。本文方法能夠?qū)⒒诰仃嚈C制的差分隱私算法的均方誤差進行一般化處理，是一種具有普遍性的方法，能夠簡潔有效地求出基于矩陣機制的差分隱私算法的均方誤差。本文以Prievlet算法[4]為例進行詳細的分析、推導，其他算法可通過類似推導完成。

本文的主要貢獻如下：

（1）基于矩陣運算以及協(xié)方差的計算，從理論上分析任意固定查詢區(qū)間下Prievlet差分隱私算法的均方誤差，得出求解公式。

（2）在第一步的基礎上，求解Prievlet算法隨機查詢區(qū)間下的均方誤差，推導出平均均方誤差的公式，得出Prievlet算法誤差的漸進階。

（3）提出精確度指標，對其進行推導、說明，并對一些算法進行求解，該指標能夠簡潔有效地說明差分隱私算法的精確性。

（4）通過實驗驗證文中所求得的均方誤差公式的正確性。

2 基礎知識與問題提出

2.1 基礎知識

差分隱私保護模型是一種強健的隱私保護框架，由Dwork等人[1]首次提出。差分隱私保護模型在數(shù)據(jù)發(fā)布過程中，不論攻擊者具備何種背景知識，都能保證隱私數(shù)據(jù)不泄露。

定義1（ε-差分隱私[1]）設有一對兄弟數(shù)據(jù)集D1和D2（當且僅當D1和D2中的記錄只有一條不同），若一個發(fā)布算法A在兄弟數(shù)據(jù)集D1和D2上的所有可能的輸出滿足以下條件，則稱算法A滿足ε-差分隱私。

定義2（ε-敏感度）統(tǒng)計某數(shù)據(jù)庫中的數(shù)據(jù)集D1和D2分別得到兩組由列向量表示的結(jié)果：Q(D1)=(x1,x2,…,xn)T，Q(D2)=(x1′,x2′,…,xn′)T。那么查詢集合Q的敏感度ΔQ滿足以下定義：

在差分隱私中，更為經(jīng)常使用的范數(shù)為1-范數(shù)，即p=1。文中的敏感度如無特殊說明均以1-范數(shù)為度量。敏感度表明了當D僅改變一條記錄的情況下對統(tǒng)計結(jié)果Q(D)的影響情況。一般而言敏感度越大，Q(D)受影響的程度越強，需要添加的噪聲也越強。

2.2 問題提出

差分隱私數(shù)據(jù)發(fā)布算法經(jīng)常需要將原數(shù)據(jù)進行線性變換后再進行發(fā)布，此時計算出每個變量的均方誤差再進行累和并不能反映該算法的均方誤差。考慮如下情景：某差分隱私算法A運行后輸出兩個隨機變量x1、x2，并計算它們的均方誤差D(x1)、D(x2)用于評價算法A。假如算法B在算法A的基礎上實現(xiàn)，其需要輸出z，滿足z=x1+x2。根據(jù)概率統(tǒng)計的原理可知，新算法輸出變量z的均方誤差為：

而由于協(xié)方差的存在，僅憑D(x1)、D(x2)是無法計算出D(z)的。該例子說明完整的均方誤差分析應該包含隨機變量之間的協(xié)方差。而在概率統(tǒng)計領域，人們常常使用協(xié)方差矩陣來表示一組隨機變量間的協(xié)方差（主對角線上的值表示均方誤差）。設X=(x1,x2,…,xn)T為一個隨機變量，則它的協(xié)方差矩陣為：

以隨機向量L?n為例，它的每一個分量均是一個滿足Lap(1)（Laplace簡稱Lap）分布的獨立隨機量，顯然隨機量間的協(xié)方差為0。而Lap(1)分布的均方誤差為2，則 L?n的協(xié)方差矩陣為：

然而，僅僅使用協(xié)方差矩陣進行誤差分析遠遠無法滿足大多數(shù)應用的需要。絕大多數(shù)算法涉及了隨機向量間的線性變換。為此，本文在誤差分析時將使用以下定理。

定理1[16]若隨機向量Z與X之間存在線性關系Z=AX（A為矩陣），且已知X的協(xié)方差矩陣表示為RX，則Z的協(xié)方差矩陣為RZ=ARXAT。

由協(xié)方差矩陣的性質(zhì)可知，其對角線元素為各隨機變量的均方誤差，因此人們通常利用函數(shù)trace(*)求解最終的均方誤差。由于忽略了協(xié)方差，該方法得出的均方誤差不能精確地表示算法的誤差。

3 Prievlet算法的誤差分析

3.1 Prievlet差分隱私算法

Prievlet差分隱私算法[4]通過對數(shù)據(jù)進行前置處理來提高數(shù)據(jù)發(fā)布的精度。這種方法受到哈爾小波變換的啟發(fā)，使用哈爾小波變換矩陣先對原始數(shù)據(jù)進行壓縮，再對壓縮后的數(shù)據(jù)添加拉普拉斯噪聲使其滿足差分隱私。然后，將原始數(shù)據(jù)與壓縮數(shù)據(jù)組合在一起構(gòu)建一棵形如圖1具有8個節(jié)點的Prievlet二叉樹，其中葉子節(jié)點為原始數(shù)據(jù)，自下而上，對于每個非葉子節(jié)點，其權值為左子樹葉子節(jié)點的權值之和減去右子樹葉子節(jié)點的權值之和。構(gòu)造過程見算法1。

Fig.1 Prievlet-two-fork-tree with 8 nodes圖1 8個節(jié)點Prievlet二叉樹

算法1Prievlet差分隱私算法

輸入：原始數(shù)據(jù)向量vi(1≤i≤2h)，隱私預算ε。

1.輸入初始數(shù)據(jù)。

2.對數(shù)據(jù)進行壓縮轉(zhuǎn)換。每個非葉子節(jié)點的值等于左子樹葉子節(jié)點的權值之和減去右子樹葉子節(jié)點的權值之和，具體公式如下所示：

3.敏感度Δ=h+1，對所有ck添加拉普拉斯噪聲得到滿足差分隱私的壓縮系數(shù)

由算法1所得到的壓縮系數(shù)，可通過式（4）還原，求出所有滿足差分隱私算法的輸出數(shù)據(jù)：

Prievlet算法適用于區(qū)間查詢，其查詢均方誤差復雜度為O(lb3n)，n=2h。相比于其他二叉樹方法，使用小波變換方法壓縮的數(shù)據(jù)，不存在不一致性問題，無需采用任何后置處理方法來提高算法的精確性。

3.2 分析Prievlet算法的均方誤差

通過研究Prievlet算法可以發(fā)現(xiàn)，數(shù)據(jù)經(jīng)過Prievlet算法的變換是線性的，這意味著可以用一種基于矩陣的運算來表示Prievlet算法的變換過程。因此，可以根據(jù)Prievlet算法的變化過程構(gòu)造相對應的策略矩陣，從而對Prievlet算法的均方誤差進行有效的分析。

首先，需將Prievlet算法的變換過程用矩陣進行表示。根據(jù)算法1，由ck的計算式（3），可以得到Prievlet算法的策略矩陣，同時根據(jù)式（4）可以得到Prievlet算法的還原矩陣。例如，當數(shù)據(jù)量的大小為4時，根據(jù)以上方法，可以得到對應的策略矩陣和還原矩陣。

Prievlet算法的策略矩陣：

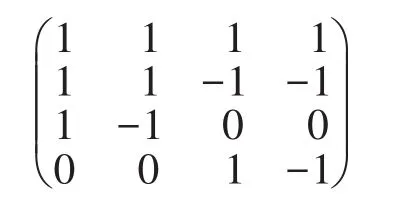
Prievlet算法的還原矩陣：

其中數(shù)據(jù)通過策略矩陣變換可得到壓縮系數(shù)，然后加噪后的壓縮數(shù)據(jù)通過還原矩陣可得到加噪后的數(shù)據(jù)。

根據(jù)文獻[4]可知，Prievlet算法是在經(jīng)過策略矩陣變換后的系數(shù)上添加噪聲，因此對策略矩陣不需要進行分析，而對于Prievlet算法的還原矩陣B，直接對加噪后的系數(shù)進行線性組合來完成還原，是均方誤差的主要來源，接下來將對其進行詳細的分析。矩陣B的構(gòu)建可根據(jù)式（4）得出，圖2是還原矩陣中單行（單個數(shù)據(jù)）的求解流程圖，整個還原矩陣B的求解見算法2。

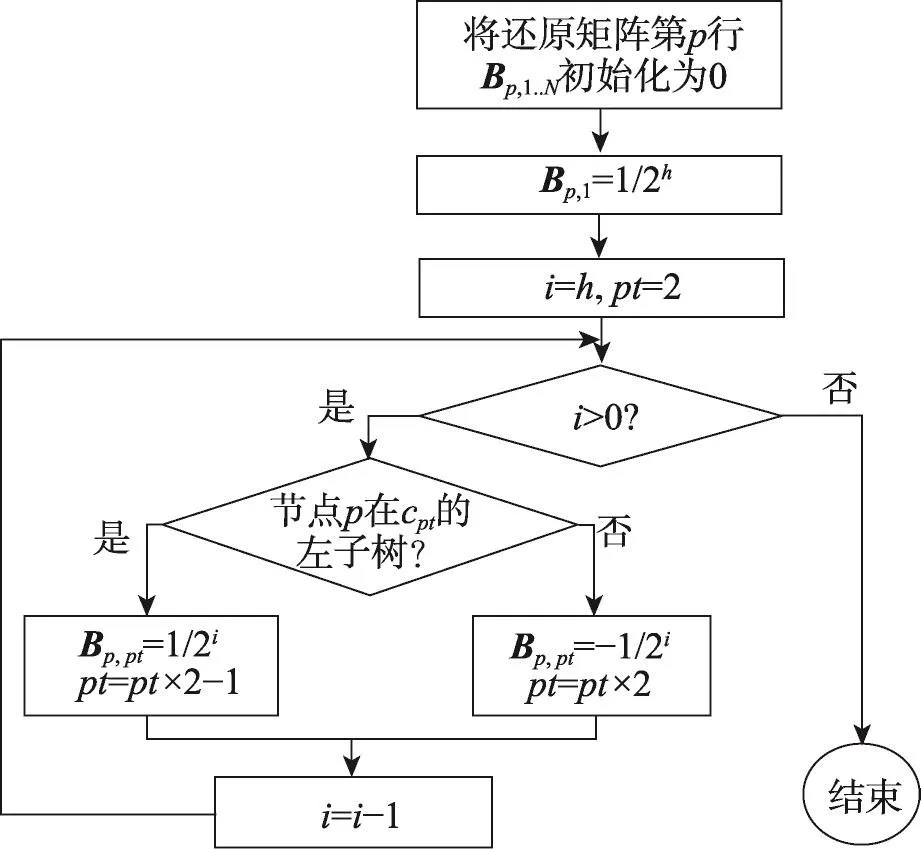
Fig.2 Flow chart to solve the p line in restore matrixB圖2 還原矩陣B第p行求解流程圖

算法2求解Prievlet的還原矩陣

通過算法2得到還原矩陣后，結(jié)合定理1，可以得到通過Prievlet算法變換后的數(shù)據(jù)的協(xié)方差矩陣：

由矩陣的乘法可知Σij為矩陣B的第i行和第 j行進行點乘的結(jié)果，且滿足如下定理。

定理2由矩陣B的第i行和第 j行點乘所得到的Σij滿足如下公式：

式中，k為節(jié)點i與節(jié)點j的最近公共祖先的高度（見圖1）。可由該公式計算求得：其中⊕表示二進制表示下的按位異或運算。

證明當i=j時，由算法2可得，恒成立。然后t從h到1循環(huán)，每次循環(huán)都將一個由0置為因此，除Bi,1以外，B的第i行存在且僅存在一個元素從而：

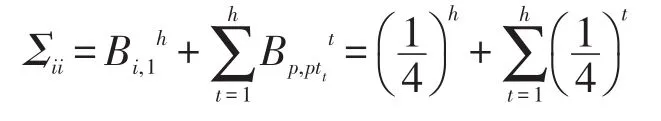
則Σij計算如下：

為了便于計算，本文對式（6）進一步化簡，得到與之等價的式（7）：

又令Φk表示兩節(jié)點最小公共祖先層數(shù)為k時的協(xié)方差，則Φk滿足如下遞推關系：

分析完Prievlet算法的均方誤差，下面對Prievlet算法的均方誤差進行求解。

3.3 求解Prievlet算法的均方誤差

求解Prievlet算法的均方誤差將分兩步進行：首先對任意固定查詢區(qū)間的均方誤差進行求解；然后求解隨機查詢區(qū)間的均方誤差。

3.3.1 求解任意固定查詢區(qū)間的均方誤差

將經(jīng)過Prievelet算法變換后的數(shù)據(jù)用向量的形式表示成則可以將查詢區(qū)間[l,r]表示成向量，那么查詢結(jié)果為

根據(jù)定理1和式（5），得到這個查詢的均方誤差為：

式（9）需要進行矩陣乘法運算，該運算的復雜度較高。而從2.1節(jié)的分析結(jié)果可以發(fā)現(xiàn)協(xié)方差矩陣存在規(guī)律，可以由定理2以及式（6）計算得出協(xié)方差矩陣中的任意一個值。利用上述特點，本文提出一個可以快速計算Prievlet算法區(qū)間查詢的均方誤差的算法。

由定理2可以得出，對于節(jié)點i與節(jié)點 j，它們的均方誤差為這意味著每對節(jié)點的均方誤差只與最近祖先高度有關。那么對每個非葉子節(jié)點進行考慮，只需計算出以該節(jié)點為最近公共祖先葉子節(jié)點的對數(shù)，再乘上對應的協(xié)方差即可。

以圖3為例，共有8個葉子節(jié)點，查詢區(qū)間為[3,7]。圖中條紋標注節(jié)點是查詢區(qū)間覆蓋了該節(jié)點的部分區(qū)間，而用灰色表示的點是整個區(qū)間都被查詢區(qū)間覆蓋。例如：節(jié)點c3所表示的是[4,8]這個區(qū)間，查詢區(qū)間[3,7]只覆蓋了其中一部分；而節(jié)點c5則完全被查詢區(qū)間[3,7]覆蓋。

Fig.3 Example of[3,7]query of Prievlet algorithm圖3 Prievlet算法查詢[3,7]的示例圖

對于灰色的節(jié)點，是被查詢區(qū)間完全覆蓋的，那么以該節(jié)點為最近公共祖先的節(jié)點對數(shù)可以由左右子樹葉子節(jié)點個數(shù)的乘積得到。根據(jù)這個二叉樹的性質(zhì)可以知道，如果該節(jié)點在第k層，那么其覆蓋范圍是2k，左右子樹葉子節(jié)點個數(shù)都為2k-1。因此，如果一個節(jié)點是第k層節(jié)點，那么以該節(jié)點為最近公共祖先的葉子節(jié)點對數(shù)為4k-1。然后只需再計算出第k層灰色節(jié)點的個數(shù)即可，可由以下公式計算：

圖3中的條紋節(jié)點是查詢邊界上的節(jié)點，顯而易見，這種節(jié)點在每一層最多會出現(xiàn)2個，因此可以直接枚舉進行求解。假設節(jié)點cx是第k層的節(jié)點，覆蓋區(qū)間為[lx,rx]，可以得出以節(jié)點cx為最近公共祖先的葉子節(jié)點對數(shù)為|P|×|R|，其中

除了考慮協(xié)方差之外，還需要對各個變量各自的均方誤差進行考慮，即Σ矩陣中的對角線元素Σii。由定理2可以發(fā)現(xiàn)，這些均方誤差都是固定的，只需將該均方誤差乘上區(qū)間的長度r-l+1即可得出。

根據(jù)上述分析，本文提出了一種求解Prievlet差分隱私算法任意區(qū)間查詢的均方誤差（算法3）。在Prievlet算法中，敏感度和隱私預算ε都是一個固定的值，這兩個參數(shù)只會影響所需添加的噪聲大小，而對于采取相同噪聲機制的差分隱私算法而言，不會產(chǎn)生影響，為了方便計算分析，暫時不予考慮，只考慮均方誤差的系數(shù)。

算法3求解任意固定區(qū)間查詢的均方誤差系數(shù)

由算法3得出的Rerr，可以得出查詢區(qū)間[l,r]的均方誤差，如下所示：

分析算法3可以發(fā)現(xiàn)，其時間復雜度為O(h)，即O(lbN)，只需遍歷一次1到h就能得出答案。因此該算法能夠完成海量數(shù)據(jù)量下的均方誤差的求解任務。

3.3.2 求解隨機查詢區(qū)間的均方誤差

算法3可以快速有效地求得任意固定查詢區(qū)間下Prievlet算法的均方誤差，但固定區(qū)間查詢的均方誤差不能體現(xiàn)該算法平均情況下的均方誤差，因此下文將在算法3的基礎上對隨機查詢區(qū)間下Prievlet算法的均方誤差進行求解，得出該算法平均情況下的均方誤差。

觀察式（9），對于所有查詢來說，Prievlet算法添加的噪聲是一樣的，其不同之處是ITΣI的值不同，本文稱這部分為均方誤差系數(shù)。接下來將對均方誤差系數(shù)進行重點分析。

觀察均方誤差系數(shù)ITΣI可以發(fā)現(xiàn)，該計算過程等價于取出Σ矩陣中的一個子矩陣，從第l行到r行，l列到r列，然后將子矩陣中所有元素相加的結(jié)果。

以下是一個在8個節(jié)點下，查詢區(qū)間為[3，7]的例子，其中矩陣是該查詢規(guī)模下的協(xié)方差矩陣，虛線框內(nèi)是被取出來的子矩陣。

接下來，對Prievlet算法的平均均方誤差進行求解。在平均情況下，可以認為對于所有的查詢區(qū)間[l,r],l≤n,l≤r≤n出現(xiàn)的概率都是均等的。可將上文中ITΣI的求解方式進行變換，考慮對于每個Σij會被多少個查詢區(qū)間所用到。計算公式如下所示：

若只考慮i≤j的情況，式（12）可以進一步化簡為 cntΣij=i×(2h-j+1)。

i＞j時，可以利用Σ矩陣的對稱性進行求解，即cntΣij=cntΣji。

從上文的分析可以看出，協(xié)方差矩陣Σ中有很多相等的值，因此可按不同的值進行分類討論，以提高求解效率。從定理2中可以看出求解總體的均方誤差可以分為兩步。

首先求解兩個不同節(jié)點的均方誤差系數(shù)之和。根據(jù)兩節(jié)點的最近公共祖先的高度劃分，假設高度為k，那么Σij滿足Σij=Φk。然后用式（13）計算這些值被每個區(qū)間計算到的總和SΦk。如下所示：

式（13）的計算過程見附錄。

然后求解每個查詢區(qū)間的各個元素的獨立均方誤差總和SD。計算過程如下：

最后，將上述兩個步驟的計算結(jié)果結(jié)合，得到區(qū)間查詢的均方誤差系數(shù)總和：

式（15）計算過程見附錄。

根據(jù)上文方法求出查詢區(qū)間的均方誤差系數(shù)總和之后，只需將其除以區(qū)間的總個數(shù)即可得到Prievlet算法在進行區(qū)間查詢時均方誤差系數(shù)的平均情況。計算過程如下：

h→∞時式（16）的極限為：

實驗表明，當 h＞10時，式（16）與式（17）計算結(jié)果的差別可以忽略不計。

最后只需要將根據(jù)式（16）得到的均方誤差系數(shù)乘上Prievlet算法的均方誤差，就可以得到平均情況下的均方誤差：

上述兩部分，基本的噪聲誤差不可變，取決于用戶想要保護隱私的程度。而誤差系數(shù)主要由所采用的算法和數(shù)據(jù)規(guī)模確定，其中數(shù)據(jù)規(guī)模取決于應用的需要，不隨所采用算法的改變而改變。為反映差分隱私算法的性能，下文將對誤差系數(shù)進行處理，將與算法性能本身無關的部分去掉，提出一種直觀的、能夠反映算法性能的評價指標。

4 O(lb3N)精確度指標

在現(xiàn)有的差分隱私數(shù)據(jù)發(fā)布領域，目前所有算法的均方誤差漸進階最低能達到O(lb3N)[15]。因此，本文將針對此類算法提出差分隱私O(lb3N)精確度指標，具體定義如下：

定義3（O(lb3N)精確度指標）已知差分隱私算法Α與該算法所處理的數(shù)據(jù)規(guī)模為N。令表示在該數(shù)據(jù)規(guī)模下算法Α產(chǎn)生的平均均方誤差系數(shù)函數(shù)，則該算法O(lb3N)精確度指標k表示為：

以Prievlet算法為例，O(lb3N)精確度指標k計算如下：

因此，隨機區(qū)間查詢下的Prievlet算法的O(lb3N)精確度指標為6。

與傳統(tǒng)的描述均方誤差復雜度的方法相比，上文提出的精確度指標能更加形象地表示差分隱私算法的性能。一般而言，精確度指標相同的算法，精確度方面性能相近；而對于精確度指標不同的算法，隨著數(shù)據(jù)規(guī)模的增大，精確度指標越低的算法，誤差越大。因此，該指標能夠準確地反映差分隱私算法的精確性。

另一方面，研究表明，絕大多數(shù)算法的O(lb3N)精確度指標均為正數(shù)，這使得結(jié)果更加直觀，能夠簡潔地反映差分隱私算法的精確性，便于人們對算法性能的研究和比較分析。經(jīng)過理論分析，常見的3種差分隱私算法，樸素二叉樹、Boost、Prievlet的 O(lb3N)精確度指標分別為1、6、6。其中關于樸素二叉樹和Boost算法的O(lb3N)精確度指標的前置分析計算過程在文獻[15]中有詳細的分析，只需將均方誤差按本文方法進一步推導即可得出，這里不再贅述；而Prievlet算法的O(lb3N)精確度指標已于前文中得出。

5 實驗分析

本文將通過實驗來驗證文中提出的求解均方誤差的算法以及公式的正確性。本文進行多次實驗，對多次實驗的誤差取平均值作為實驗誤差。同時通過算法3以及式（17）計算出相對應的理論誤差，將兩者進行比較，來驗證本文理論分析的正確性。

本文實驗是在奔騰雙核CPU T4200 2.00 GHz的計算機下完成。采用的語言為Matlab，實驗中差分隱私參數(shù)ε統(tǒng)一設置為1。

5.1 驗證任意區(qū)間查詢誤差算法

為了能夠體現(xiàn)出實驗效果，同時考慮實驗需要消耗的時間，本文所采取的數(shù)據(jù)規(guī)模為1 024。隨機生成了50個查詢區(qū)間，分別計算理論上和實驗實際產(chǎn)生的均方誤差。每個查詢區(qū)間重復實驗100次，將每次所產(chǎn)生的均方誤差取平均作為最終的實驗結(jié)果，而理論誤差則通過算法3計算。詳細實驗結(jié)果如表1所示。

為了讓讀者更加直觀地比較理論誤差與實驗誤差，將表1中的數(shù)據(jù)制作成折線圖，如圖4所示。

Fig.4 Comparison of experimental error with theoretical error in fixed query interval圖4 固定查詢區(qū)間下實驗誤差與理論誤差的對比圖

觀察圖4可以發(fā)現(xiàn)，總體上實驗結(jié)果與理論結(jié)果還是比較接近的，而且實驗產(chǎn)生的誤差圍繞著理論誤差上下波動，符合差分隱私所添加噪聲是隨機的這一特點。此外，表1中，有的查詢區(qū)間實驗結(jié)果與理論結(jié)果較接近，而有的則相差較大，這說明查詢區(qū)間的不同產(chǎn)生的誤差波動程度不一，這也是由于實驗次數(shù)不夠多，隨著實驗次數(shù)增多，所有的查詢區(qū)間的誤差會與理論誤差越來越接近。

5.2 驗證平均區(qū)間查詢誤差算法

接下來，將對前文分析得出的Prievlet算法在平均情況下的均方誤差進行實驗論證。為了更好地驗證該理論分析的正確性，本文對所有可能的區(qū)間進行實驗，最終取平均值作為實驗結(jié)果。本次實驗采用的數(shù)據(jù)規(guī)模為N=2m,0≤m≤10，共10組模擬數(shù)據(jù)進行實驗對比。與上個實驗一樣，本實驗也進行了100次重復實驗，之后取平均值作為實驗結(jié)果，并根據(jù)式（17）計算得出理論上的均方誤差進行比較。實驗結(jié)果如表2所示。

Table 1 Results of two errors in fixed query interval表1 固定區(qū)間查詢下兩種誤差的計算結(jié)果

Table 2 Experimental error and theoretical error in mean case表2 平均情況下的實驗誤差與理論誤差

為了方便觀察,將實驗結(jié)果用折線圖的方式表示。實驗結(jié)果如圖5所示。

Fig.5 Comparison of experimental results with theoretical results in mean case圖5 平均情況下實驗誤差與理論誤差的對比圖

從圖5可明顯地看出，實驗結(jié)果與分析結(jié)果幾乎一樣，進一步說明了式（17）計算出的Prievlet算法均方誤差能準確地反映算法性能，驗證了該公式的正確性。

6 結(jié)束語

本文利用矩陣機制的相關理論，分析了以Prievlet算法為代表的基于矩陣機制的差分隱私數(shù)據(jù)發(fā)布方法的理論誤差，成功求解了Prievlet算法在任意區(qū)間查詢下的均方誤差和平均情況下的均方誤差公式。并在此基礎上提出了可有效衡量具有相同誤差漸進階的不同差分隱私發(fā)布算法之間性能差異的精確度指標。

附錄：