剪跨比不大于2.0的RC剪力墻力-位移全過程計算

陳曉磊　傅劍平,　甘金鳳,　薛　峰

(1. 重慶大學土木工程學院, 重慶 400045; 2.中冶建工集團有限公司, 重慶 400080;3. 重慶大學山地城鎮建設與新技術教育部重點實驗室, 重慶 400045)

鋼筋混凝土剪力墻因其整體性好,布置靈活,側向剛度大等優點被廣泛用于實際工程中[1-2],其中剪跨比r≤2.0的剪力墻常被用于結構設計.經研究[3]發現,這類剪力墻在荷載作用下構件內部的應力及應變場呈不連續的特性,平截面假定已不再適用.為此國內外學者提出了多種宏觀力學模型對其進行研究,其中軟化桁架模型及拉壓桿模型比較具有代表性.軟化桁架模型于1985年由Hsu等提出,隨后得到了Gupta等的發展[4-6],該模型假定剪力墻腹板應力均勻分布,但依據Saint-Vanant原理[7]這與以剪切為主的剪力墻實際受力行為不符.相比于該模型,拉壓桿模型則根據構件內主應力分布特征進行建模,能真實反映剪力墻的受力特性,該模型由Ritter[8]提出,隨后Hwang對其進行了改進,并用于節點及剪力墻水平承載力的計算[9-12].2002年Hwang和Lee[13]提出了簡化拉壓桿模型;2005年Yu等[14]應用拉壓桿模型對62個剪力墻進行承載力、剪切傳遞路徑及破壞模式的預測;2014年KASSEM等[15]對拉壓桿模型進行簡化以便于工程應用;劉霞等[16]于2013年將拉壓桿模型用于鋼筋混凝土開洞深梁的抗剪承載力計算;2016年田建勃等[17]應用考慮軟化效應的拉壓桿模型對鋼板混凝土組合連梁的受剪承載力進行分析.此外Bali[18]還提出了一種計算剪力墻最大承載力及對應變形的拉壓桿模型.Young[19]提出了一種基于彈性有限元的非線性拉壓桿模型求解方法.

到目前為止拉壓桿模型已能用于預測剪跨比不大于2.0的剪力墻的水平承載力、剪切傳遞路徑及失效行為.但對于剪力墻力-位移全過程計算的研究則進展緩慢,其主要因為模型缺少桿件間的變形協調條件.因此本文基于拉壓桿模型的概念,通過引入合理的變形協調條件,再結合力的平衡條件及物理方程建立了可計算低矮剪力墻力-位移全過程的改進拉壓桿模型.

1　改進拉壓桿模型的合理化假定

改進拉壓桿模型由主拉壓桿模型(圖1)及分布筋拉壓桿模型(圖2)組成,模型假定如下:

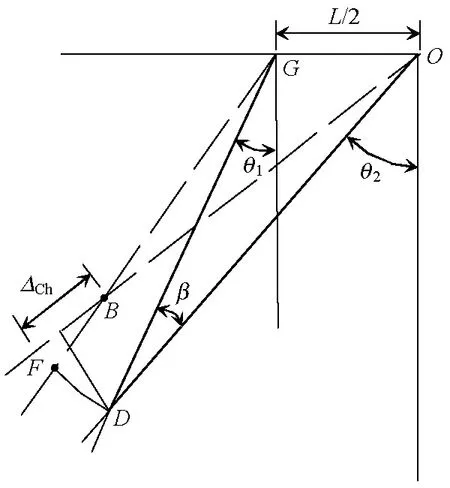
(1) 圖1中兩根相互平行的橫向次斜壓桿(OC桿和GD桿)及豎向次斜壓桿(AD桿和OE桿),在墻肢變形過程中始終保持平行且壓應變相同.水平及豎向拉桿CG桿和EA桿分別由上下及左右相鄰分布筋構成.BD桿及OF桿均由邊緣約束區縱筋組成,圖中:L為剪力墻墻肢高度.

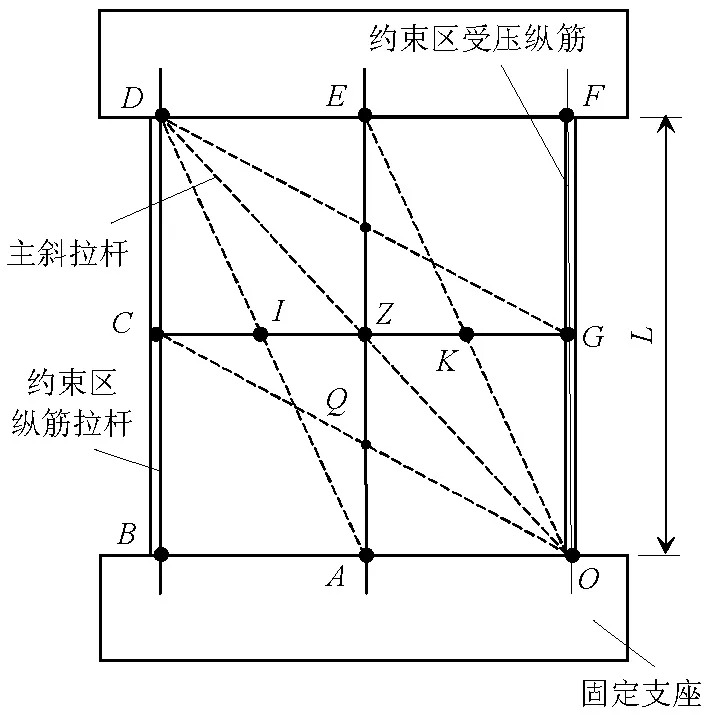
圖1　主拉壓桿模型Fig.1　Main strut-tie model

(2) 墻肢發生變形時,假定OC桿相對于支座轉角Δθ1、OD桿相對于OC桿轉角Δθ2及OE桿相對于OD桿的轉角Δθ3相等,變形前后各桿件位置保持不變(即:假定OC桿、OD桿及OE桿與底部截面OB桿的傾角θ1、θ2及θ3不變).

圖2(a)中,以主斜壓桿OD為界,將試件分為彎剪受拉區OBD及彎剪受壓區ODF.在OBD中,邊界OB與OC所圍區域為H1區,OC與OD所圍區域為H2區.各區域間的次生斜壓桿一端指向O點,另一端與水平分布筋端頭連接,并假定次生壓桿水平分力與對應連接的水平分布筋拉力平衡.當墻肢發生轉動時,H1、H2區各次生壓桿相對轉角總和分別為Δθ1及Δθ2,且每根次生壓桿轉角與該桿所在區域下邊界間的夾角呈正比,而桿件軸向應變則由所在區域邊界桿件應變通過線性插值求得.

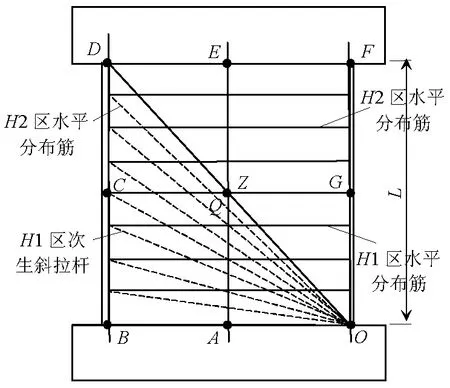
(a) 水平分布筋

圖2(b)中,假定各縱筋應變沿墻肢高度方向呈線性分布且在墻肢頂端應變為0.邊界OF及AE桿所圍區域為V1區,AE及BD桿所圍區域為V2區.EA、BD桿變形分別由OE、OD桿的變形引起;OF桿與混凝土粘結良好,該桿件O點處應變可通過莫爾線性應變理論求得,再依應變分布假定求其變形量.各區間縱向分布筋變形量可通過邊界桿件變形量進行線性插值求得.

(3) 假定剪力墻所提供的水平抗力由主斜壓桿壓力水平分量及水平分布筋拉力構成,豎向抗力由主斜壓桿壓力豎向分量及豎向鋼筋所產生的軸力構成.各桿件連接節點視為理想鉸,忽略鋼筋與混凝土間的粘結滑移.鋼筋采用二折線本構模型,混凝土采用考慮軟化效應的本構模型,混凝土主壓應力為

(1)

式中:ε0=0.002;

fc為混凝土峰值壓應力;

v為混凝土軟化系數,v=1/(0.8+170εr),εr為主拉應變;

εd為混凝土主壓應變.

2　改進拉壓桿模型各桿件變形計算

假設墻肢頂端發生水平位移Δ由主斜壓桿轉動及其軸向壓縮變形ΔCx共同組成.若混凝土主斜壓桿OD的受壓應變為εCx,幾何關系如圖3所示.圖中ΔCx=(εCxL)/sinθ2.

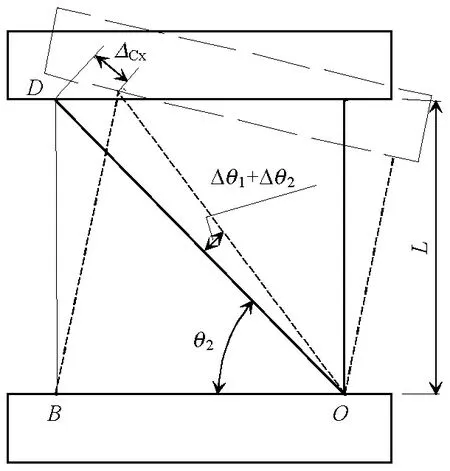
(a) 整體圖

(b) 局部圖圖3　主斜壓桿OD的轉角變形計算Fig.3　Calculating rotational angle of main diagonal strut OD

由圖3可得,頂端位移Δ與主斜壓桿轉角(Δθ1+Δθ2)及對應壓應變εCx的幾何關系為

Δ=L(Δθ1+Δθ2)+εCxL/tanθ2.

(2)

根據假定(2),利用式(2)可得主斜壓桿及橫(豎)向次斜壓桿轉角為

Δθ3=Δθ1=Δθ2=(Δ-εCxL/tanθ2)/2L.

(3)

2.1　豎向及橫向次斜壓桿變形計算

對于豎(橫)向次斜壓桿的變形計算,根據假定(1),只需求其中一根豎(橫)向次斜壓桿變形即可.選取圖1中次斜壓桿AD及GD進行變形計算,如圖4所示.

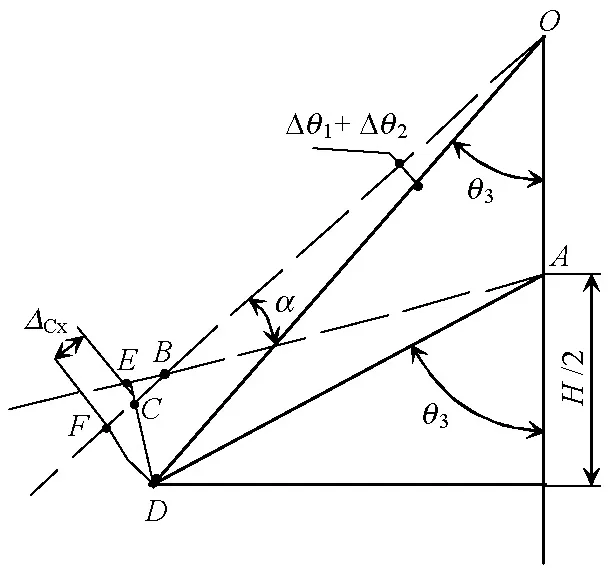
(a) 豎向次斜壓桿AD

(b) 橫向次斜壓桿GD圖4　次斜壓桿變形計算Fig.4　Deformation of sub-diagonal strut

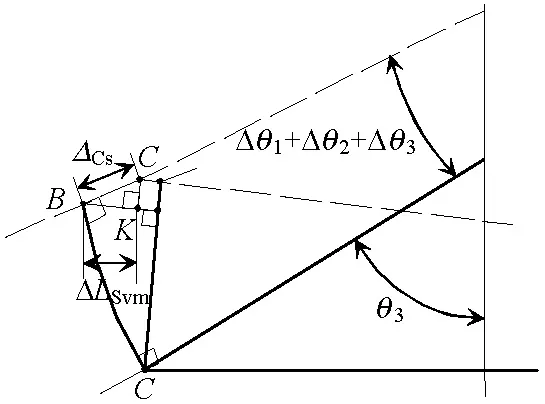
圖4(a)中,當主斜壓桿OD繞O點發生Δθ1+Δθ2的轉動及ΔCx的壓縮變形時,桿端從D移至B,從而帶動AD桿發生Δθ3的轉動并產生EB軸向變形ΔCs.由圖4(a)幾何關系可知:

(4)

類似的,圖4(b)中壓桿GD的變形ΔCh為

(5)

式(4)、(5)中:α=θ3-θ2;

β=θ1-θ2.

2.2　水平向拉桿及分布鋼筋變形計算

彎剪受壓區水平拉桿及水平分布筋與混凝土粘結良好,錨固可靠.墻肢發生變形時,各水平桿件均繞該桿件與OD桿的交點進行轉動.圖1中拉桿CG變形由OC桿變形引起,如圖5所示.當OC桿發生Δθ1轉動并產生ΔCh壓縮變形時,CG桿由C移至A并發生ΔLShm的伸長.

ΔLShm=tanθ1HΔθ1-HεCh,

(6)

式中:εCh為橫向次斜壓桿的軸向壓應變,εCh=(ΔChcosθ1)/H.

圖5　水平向拉桿CG的變形計算Fig.5　Model of horizontal tie’ deformation

依據假定(3)可得各水平分布筋變形.由于篇幅限制,僅對H1區水平分布筋變形量進行推導,H2區的僅給出計算結果.對各區間水平分布筋及相應次生壓桿從下至上依次編號為1、2、nH1(nH2).nH1及nH2為

(7)

(8)

式(7)和(8)中:S為水平分布筋間距;

QH1為H1區中第一道水平分布筋與墻肢底部截面距離;

QH2為H2區中第一道水平分布筋與水平桿CG之間的垂直距離.

H1區水平分布鋼筋變形計算如圖6所示.

圖6(a)中Si為H1區第i道水平分布筋與墻肢底部間的距離.墻肢發生變形時(圖6(b)),第i根次生斜壓桿繞Oi點發生δi的轉動及εi的壓縮應變,相連分布筋伸長量為

ΔLi=Liδisinφi-Liεicosφi,

(9)

式中:Li及φi分別為H1區第i根次生斜壓桿的桿長及壓桿與墻肢底部的夾角;

墻肢轉動角δi及相應應變εi可依假定(3)求得,如式(10)、(11).

δi=(φnH1-φi)(Δθ1/θ1),

(10)

εi=(εCh/φnH1)φi,

(11)

式中:φnH1為H1區第nH1道水平分布筋與墻肢底部截面夾角.

同理可得H2區第j根水平分布筋變形ΔLj與相應次生斜壓桿壓縮應變εj間的關系為

ΔLj=Ljδjsinφj-Ljεjcosφj,

(12)

式中:Lj、φj分別為H2區第j根次生斜壓桿桿長及壓桿與OC桿間的夾角;

δj為該桿件隨墻肢變形發生的轉角.

(a) H1區水平筋拉桿變形

(b) 第i道水平筋拉桿變形計算圖6　H1區水平分布筋變形計算示意圖Fig.6　Deformation of H1 horizontal reinforcement

2.3　豎直方向各桿件的變形計算

當墻肢發生變形時,依假定(3),圖1中豎向拉桿EA及BD的縱向伸長量ΔLSvm及ΔLSvl可認為是與其頂端節點D,E相連的斜壓桿變形產生.依據圖7(a)和(b),ΔLSvm及ΔLSvl計算結果為

ΔLSvm=Lcotθ3(Δθ1+Δθ2+Δθ2)-

ΔCssinθ2,

(13)

ΔLSvl=LΔθ2/tanθ2-ΔCssinθ2,

(14)

而對于OF桿,依假定(3),O點處壓應變εSvy及桿件變形量ΔLSvy計算結果為

εSvy=εCxsin2θ2,

(15)

ΔLSvy=0.5L2εSvy.

(16)

通過上述推導得知V1、V2區邊界桿件OF、EA及BD的變形量.應用線性插值可求圖2(b)中V1、V2區豎向分布筋變形量,計算結果為

(17)

(18)

式中:ΔLsk(ΔLsl)為V1(V2)區第k(l)道縱向分布筋的變形量;

xk(xl)為V1(V2)區第k(l)道豎向分布筋距O點和EA桿的水平距離.

各區間豎向分布筋編號從右向左依次為1、2、…、k(l)、…、nV1(nV2).

(19)

式中:SV為豎向分布筋間距;

QV1為V1區第一根豎向分布筋距O點的水平距離.

(a) 拉桿EA的變形

(b) 拉桿BD的變形圖7　EA桿與BD桿的變形計算示意圖Fig.7　Model of EA and BD vertical ties’ deformation

3　改進拉壓桿模型各桿件受力計算

3.1　主斜壓桿受力計算

已知主斜壓桿壓應變εCx,桿件壓力TCx為

(20)

式中:b為墻肢厚度;

w為主斜壓桿高度,其計算表達式為

w=[0.25+0.85(N/fcAw)]H,

(21)

式中:N為軸向壓力;

Aw為墻截面面積.

軟化系數計算式中,可根據變形協調條件求得[6]橫向拉應變εr.

εr+εCx=εh+εv.

(22)

依假定(1)可知,圖1中橫(豎)向次斜壓桿相對于主斜壓桿轉動所引起的拉桿變形可認為是以Z為中點對稱的.因此假定εh及εv與拉桿CG的KZ段及拉桿AE的QZ段平均應變相同.依據圖8,εh及εv計算結果為

εh=2Δθ3tanθ2,

(23)

εv=2Δθ2tan(0.5π-θ2).

(24)

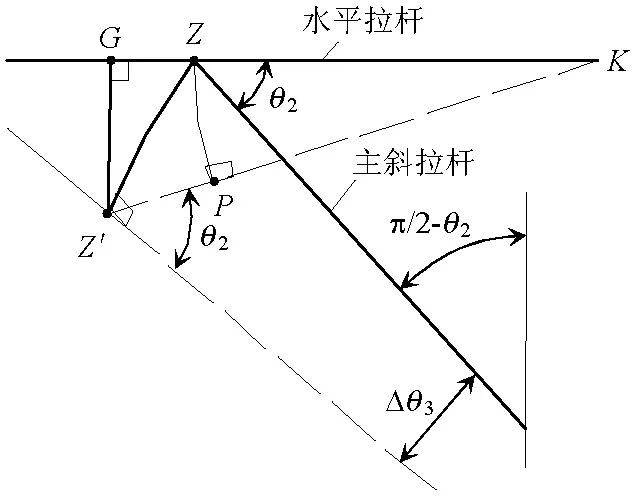
(a) 水平拉桿

(b) 豎向拉桿圖8　應變計算示意圖Fig.8　Stress of horizontal tie and vertical tie

3.2　水平分布筋受力狀態計算

由于彎剪受壓區作為水平分布筋可靠錨固端,受拉區忽略混凝土與鋼筋的粘結作用.由此可得每根水平分布筋受力狀態,以H1區為例受力狀態如圖9所示.

圖9　水平分布筋受力狀態示意圖Fig.9　Load condition of horizontal reinforcement

根據圖9建立如式(25)的平衡方程:

(25)

式中:Et、Ai分別為所求水平分布筋彈性模量及截面面積;

TPi、τPi分別為水平分布筋受拉端拉力及整體受壓區粘結應力.

根據水平分布筋所在區域由式(9)和(12)得到ΔLi.通過解方程組得:

TPi=(2ΔLiEtAi)/(Li+H).

(26)

類似的水平拉桿CG受力為

(27)

式中:AShm為CG桿截面面積;

LShm為CG桿長度.

3.3　縱向分布筋及邊緣約束區縱向桿件受力計算

依據假定(3)縱向桿件沿墻肢高度方向的應變分布特性可求各桿件受力.設圖2(b)中V1、V2區各道豎向桿件受力為TZk和TZl.當縱向分布鋼筋未屈服時其受力為

TZk=(ΔLskEtAk)/L,

(28)

TZl=(ΔLslEtAl)/L,

(29)

式中:Ak為V1區第k道豎向桿件的截面面積;

Al為V2區第l道豎向桿件的截面面積.

同理可得DB桿、OF桿及EA桿在桿件屈服前的受力為

TSvl=ΔLSvlEtASvl/L,

(30)

TSvy=ΔLSvyEtASvy/L,

(31)

TSvm=ΔLSvmEtASvm/L,

(32)

式中:ASvl、ASvy及ASvm分別為DB、OF及EA桿的截面面積.

4　改進拉壓桿模型平衡方程的建立

依據假定(4),墻肢豎向平衡方程表達式為

TSvm+TSvy+Svl-N,

(33)

式中:TF為墻底端截面法向合力.

墻肢水平向抗剪承載力Vwh為

(34)

式中:TPj為H2區第j根水平的分布筋受拉端拉力.

5　改進拉壓桿模型計算框圖

通過合理假定建立各桿件之間的變形協調關系,并結合物理方程及平衡方程構建了計算剪力墻力-位移骨架曲線的改進拉壓桿模型.

應用MATLAB編制程序SW對其進行計算,計算流程如圖10所示.

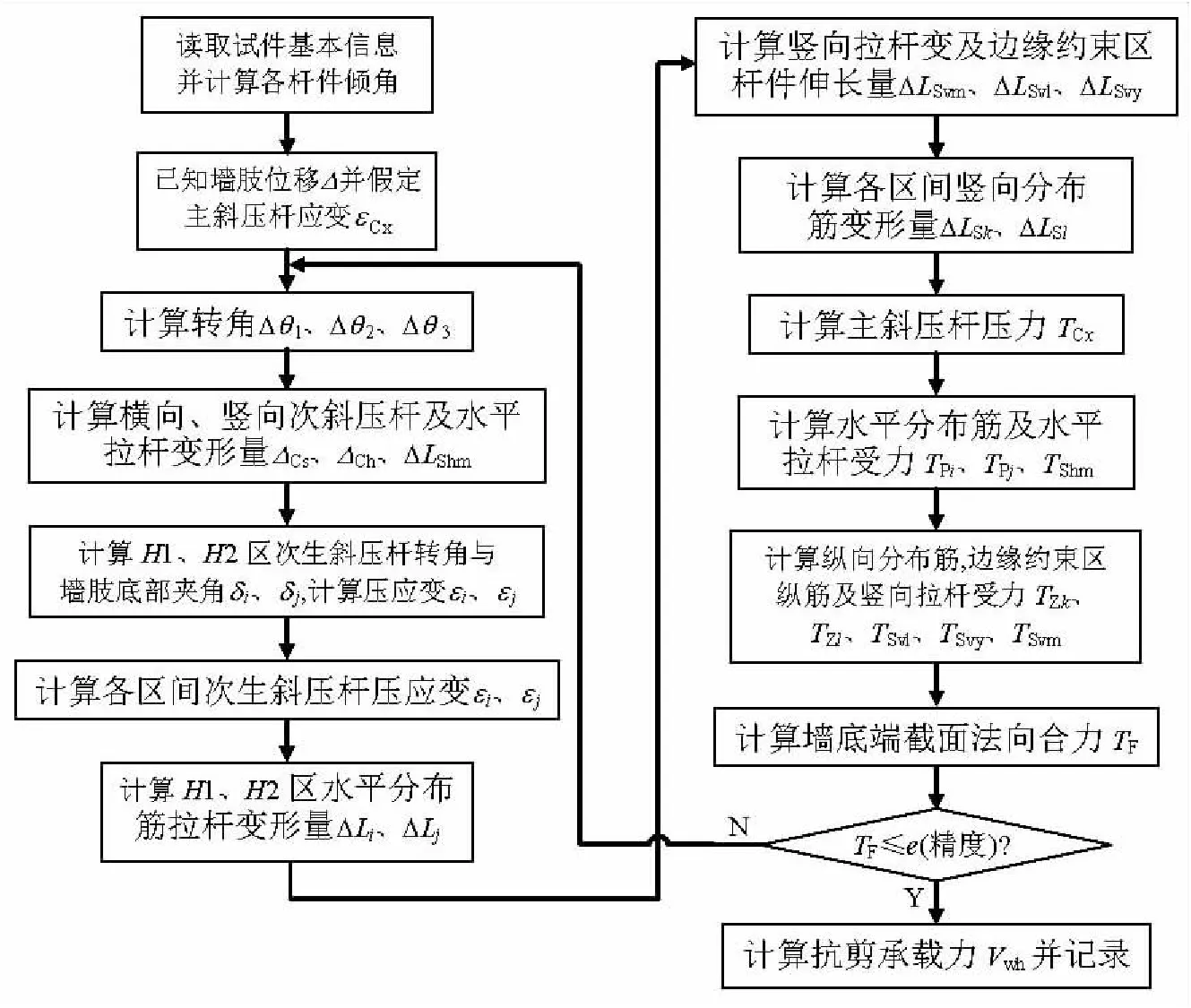
圖10　SW程序計算主框圖Fig.10　Main diagram of SW program

6　算例分析

應用程序SW對6片剪力墻試件[20-23]進行力-位移(P-Δ)骨架曲線計算,為統一表達,墻肢頂點位移Δ用位移角β(Δ/L)表示,對比結果如圖11所示.各位移級迭代次數信息由表1所示.

從圖11中可知,程序SW計算所得P-β骨架曲線與試驗記錄在各受力階段總體吻合較好,該程序可在一定程度較好地模擬剪切型鋼筋混凝土剪力墻P-β骨架曲線.表1中6個試件各位移級迭代次數基本保持在16～23次之間,且各級位移迭代次數差別不大,總體較為一致.

表1試件各級位移迭代次數
Tab.1Iterations of specimens in each displacement level

次

試件編號1級位移2級位移3級位移4級位移5級位移6級位移7級位移8級位移SW1.5-21616141518192322SW2.0-11718181719192024SW-16191820191819——SW-251818202021201923SJ-1181719192018——SJ-219171920181816—

注:“—”表示試件未進行該位移級加載.

7　改進拉壓桿模型參數分析

本節將對r≤2.0的剪力墻進行參數分析,并研究各參數對剪力墻P-β骨架曲線的影響.以下參數分析均以試件SW1.5-2為基礎展開,結果如圖12～14及表2.

7.1　軸壓比影響

改變試件頂部向軸壓力,分別取軸壓比0.1、0.2、0.3、0.4及0.5進行模擬.計算結果如圖12所示.

圖12　不同軸壓比下的P-β骨架曲線Fig.12　P-β skeleton curves for various axial load

由圖12及表2可知,隨軸壓比不斷提高,剪力墻的最大承載力不斷上升,但上升幅度隨軸壓比增大而逐漸減少,當軸壓比超過0.4時增長幅度減緩,初期剛度隨軸壓比的增加而增大.

7.2　剪跨比影響

對不同剪跨比的剪力墻P-β骨架曲線進行模擬,如圖13,承載力計算結果列于表2中.由圖13及表2可知,隨剪跨比的減少,剪力墻的最大承載力增加,初期加載剛度增加.

7.3　分布配筋率影響

不同分布配筋率(橫豎向分布配筋率均一致)作用下模擬結果如圖14和表2所示.隨分布配筋率提高,剪力墻的最大抗剪承載力有所增加.但相比于軸壓比作用的影響,其增長幅度相對較小.隨分布配筋率的提高,剪力墻初期加載剛度變化不顯著.

圖13　不同剪跨比下的P-β骨架曲線Fig.13　P-β skeleton curves for different shear span ratios

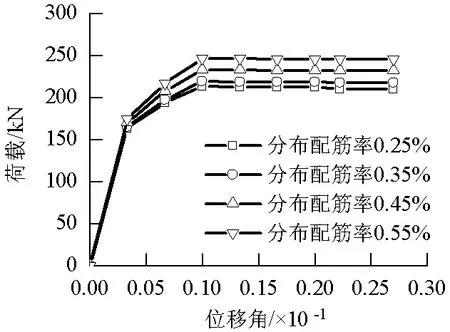
圖14　不同分布配筋率下的P-β骨架曲線Fig.14　P-β skeleton curves for different distribution reinforcement ratios

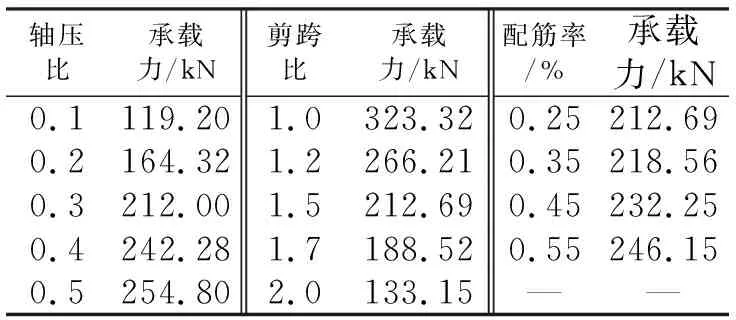
軸壓比承載力/kN剪跨比承載力/kN配筋率/%承載力/kN0.1119.201.0323.320.25212.690.2164.321.2266.210.35218.560.3212.001.5212.690.45232.250.4242.281.7188.520.55246.150.5254.802.0133.15——

8　結　論

(1) 本文基于拉壓桿模型的概念,通過引入變形協調條件,并結合平衡方程及物理方程建立了適用于r≤2.0的剪切型剪力墻力-位移全過程計算的改進拉壓桿模型.

(2) 應用改進拉壓桿模型對6片剪力墻試件的力-位移骨架曲線進行模擬.結果表明,與試驗結果吻合較好.

(3) 應用模型進行參數分析,得知剪力墻的最大承載力及初期加載剛度隨軸壓比增加而增大;隨剪跨比的增加,最大承載力降低;隨墻體配筋率的增長,承載力增長不顯著.