復雜空間形態邊坡的穩定性分析

武小菲,　楊　濤,　武琨璐,　李　輝, 艾　揚,　申少華,　王　鷹

(1. 西南交通大學土木工程學院, 四川 成都 610031; 2. 四川電力設計咨詢有限責任公司, 四川 成都 610041; 3. 廣西交通科學研究院有限公司, 廣西 南寧 530007; 4. 西南交通大學地球科學與環境工程學院, 四川 成都 610031; 5. 西藏大學工學院, 西藏 拉薩 850000)

邊坡穩定常用的分析方法包括二維剛體極限平衡法[1-2]、塑性極限分析法[3-5]和有限元強度折減法[6-7].經過長期的發展和應用,均積累了豐富的使用經驗,保證了邊坡工程的運營安全.隨著工程建設的大規模發展,所涉及的邊坡工程空間形態越來越復雜.例如水電高邊坡、礦山高邊坡、隧道洞門高邊坡等,一般均具有復雜的臨空面條件或空間邊坡面形態.這些邊坡體內的應力狀態具有明顯的空間差異性,邊坡穩定性問題也成為三維問題,再難簡化為平面問題而采用二維分析.截至目前,尚無公認的成熟的邊坡三維穩定性分析方法.

邊坡的破壞具有漸進發展過程[8-10],需要提出更合理的穩定性計算指標,以指導不同變形階段的邊坡穩定性評價,據此采用相適宜的支擋結構措施.王毓泰首先采用巖體應力與強度的比值定義邊坡點安全系數[11],以此評價邊坡的局部穩定性.吳家冠則考慮了巖土體的剪切破壞,點安全系數定義中引入Mohr-Coulomb強度準則,定義邊坡點安全系數為抗剪強度與剪應力水平的比值[12],即

(1)

式中:c、φ分別為截面的黏聚力和內摩擦角;σ、τ分別為截面上的正應力和剪應力.

邊坡體從彈性狀態發展為塑性狀態過程中,這一定義是合理的,也邊坡工程中得到應用[13-14].邊坡體在形成貫通破裂面的過程中,破裂面的發展方向受到周圍土體的限制,需要適應整個邊坡體的應力發展狀態,而不是僅僅取決于一點自身的應力狀態.也就是說,邊坡宏觀破裂面并不一定與塑性力學的最危險破裂面一致，基于此,楊濤等假定邊坡臨界失穩的位移等值面與潛在失穩滑動面一致,在位移等值面上定義了邊坡點安全系數[16].但在實際應用中發現,隨著邊坡漸變失穩,各階段位移場并不一致,導致了計算結果的多樣性.為此,本文基于復雜空間形態的邊坡分析,進一步探討邊坡空間點安全系數的計算步驟.

1　邊坡點安全系數

數值計算方法廣泛應用于邊坡穩定性分析中,其可靠性已經得到業界公認.對于復雜空間形態的邊坡體只能借助于三維數值分析方法才能獲得可靠的應力場和位移場.但僅僅依據應力場和位移場計算成果,尚不便于工程設計應用.工程界習慣于采用量化安全儲備程度的安全系數為指標對邊坡的穩定性狀態進行評價.

1.1　基于位移等值面的點安全系數

當邊坡體發生明顯失穩滑移時,滑移面上下部分巖體具有明顯的位移差,即在滑移面處形成了位移間斷.該位移間斷處,即是位移等值面通過的位置.也就是說,邊坡失穩的滑移面與位移等值面具有一致性.

對于滑坡,可以在滑移面上定義點安全系數[15],其物理意義明確,概念清晰；對于邊坡,由于沒有明確的滑移面,可以假定位移等值面即是滑移面,將點安全系數定義在位移等值面上[16].

位移等值面選用Bezier雙三次曲面擬合.Bezier雙三次曲面的參數表達式為

u,w∈[0,1],

(2)

(3)

式中:u、w為擬合參數;Pij為控制點,Bi,3(u)、Bj,3(w)均為為Bernstein基數函數；Bj,3(x)類似式(3)，其中，x=u，w.

可求得位移等值面單位法向量為

(4)

結合邊坡體空間應力狀態,可得σ和τ分別為

(5)

式中:px、py、pz為斜截面上的正應力分量.

據此,定義邊坡點安全系數為

(6)

式中:τu為計算點的抗剪強度.

1.2　整體安全系數

基于位移面上的點安全系數,可定義位移等值面上的平均點安全系數為邊坡整體安全系數,即

(7)

式中:l為等值面上單元總數;Fk為單元k的安全系數;Ak為單元k所代表的等值面面積.

對所有等值面計算整體安全系數,其最小值即為邊坡整體安全系數.

1.3　狀態分析

在邊坡應力演化發展過程中,邊坡體位移場由小到大,位移等值面形態在不斷變化.只有當邊坡體處于臨界失穩狀態或者發生大變形以至于計算不收斂時,其位移等值面才能代表邊坡最終失穩的滑動面.此時的位移等值面形態也是穩定的.

然而,邊坡的實際工作狀態不一定是臨界狀態,甚至是沒有發生任何變形的初始狀態，這時候計算域內的位移場與臨界狀態不一致.為了協調當前狀態應力場與臨界失穩狀態位移場的關系,本文提出采用FLAC3D軟件分3步計算邊坡點安全系數：

(1) 計算臨界狀態的位移場.通過強度折減等方法降低邊坡體抗剪強度參數,使邊坡處于臨界狀態或者大變形狀態.利于FLAC3D的FISH語言編寫節點信息輸出程序,使用內置gp_statesave函數輸出節點位移信息.

(2) 計算當前狀態的應力場.設置實際的邊坡巖土體物理力學參數,計算當前狀態應力場.利于FLAC3D的FISH語言編寫單元信息輸出程序,使用內置z_statesave函數輸出單元應力信息.

(3) 建立點安全系數計算文件.利于FLAC3D的FISH語言編寫節點信息輸入和單元信息輸入程序,使用內置gp_staterest函數導入節點信息,使用內置z_staterest函數導入單元信息.

點安全系數計算文件內同時具有了極限狀態的位移場和當前狀態的應力場,可以計算點安全系數.

2　案例分析

本文以貞豐縣煤電冶一體化工業園熱電聯產動力車間項目為例，工程位于貴州省貞豐縣白層鎮,主要建筑包括主廠房、鍋爐、煙囪、輸煤系統、變壓器、脫硫建筑物等.

2.1　地形地質特征

邊坡研究區位于白層鎮北盤江右岸,那郎河右岸與北盤江交匯處，場區地貌屬于構造溶蝕-侵蝕地貌,表現為低中山地形,山體連綿起伏,山體渾厚,溝谷發育,東側為北盤江(水面約352.7 m)、北側為那郎河,山頂高于谷底約270 m,廠址位于新建二級道路之上,總體坡度為25°～35°,部分大于40°,局部有高約3～5 m的陡坎分布.

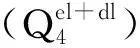
頁巖呈灰黃-灰綠色,黏土礦物為主,泥狀結構,薄片層狀構造,垂直裂隙較發育,巖體破碎,裂面有褐黃色Fe、Mn質薄膜渲染,巖芯多呈碎塊狀、短柱狀,強風化,局部風化為土狀,層厚一般4.0～10.6 m,產狀195 ～272°∠8 ～55°,埋深1.7～6.9 m,邊坡全場地分布.泥灰巖呈深灰色,主要礦物為方解石及黏土礦物,泥狀結構,中厚-厚層層狀構造,巖體較破碎-較完整,裂面有褐黃色Fe、Mn質薄膜渲染,巖芯多呈短柱狀、柱狀、長柱狀,部分碎塊狀,強風化帶厚一般0～5.3 m,產狀195～272°∠8 ～55°,下伏于頁巖之下,埋深6.9～14.3 m,邊坡全場地分布.

據勘察資料,推薦強風化頁巖、泥灰巖的天然重力密度γ=22.0 kN/m3,粘聚力c=50 kPa,內摩擦角φ=25°,泊松比μ=0.30，彈性模量E=100 MPa;中風化泥灰巖的γ=25.0 kN/m3,c=150 kPa,φ=25°,μ=0.20，φ=32°,E=500 MPa.

2.2　工程邊坡設計

運煤道路是電廠燃煤的運輸通道,是在原自然邊坡的基礎上開挖形成.其中K0+250 m～K0+470 m段最為高陡,最大工程邊坡高度達到43 m,是運煤道路的控制性工程.其設計工程邊坡平面如圖1所示,典型斷面如圖2所示.邊坡沿線路方向長220 m,共分為5級開挖,邊坡坡比為 1∶1.5～1∶5.3.下部邊坡開挖量大,揭露中風化巖層,坡比較大,為 1∶1.5.上部邊坡主要為強風化基巖,坡比較小,取 1∶5.3.各級邊坡豎直高度不大于8 m.各級邊坡頂部設置2 m平臺.

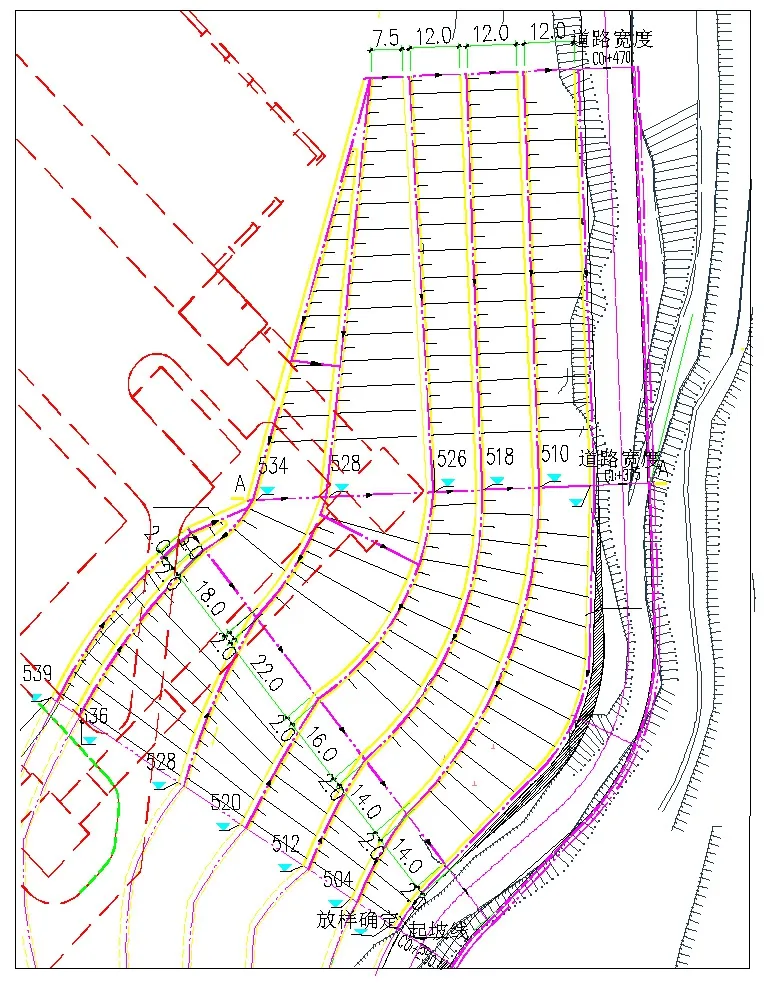
圖1　工程邊坡平面(單位：m)Fig.1　Planar graph of engineering slope(unit： m)

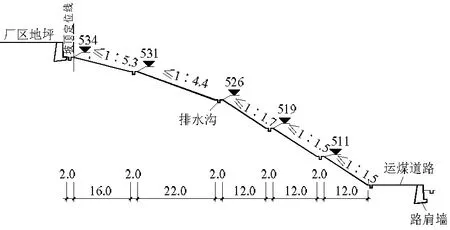
圖2　工程邊坡斷面(單位：m)Fig.2　Section gragh of engineering slope(unit： m)

3　邊坡三維穩定性分析

工程邊坡位于地形外凸的山坡地帶,路面傾斜,高程從496 m升高到512 m,各級邊坡線呈弧狀,邊坡具有復雜的空間形態,按照規范采用二維剛體極限平衡法不能準確評價邊坡的穩定性,需要建立三維數值計算模型,采用點安全系數進行穩定性分析.

3.1　三維計算模型

依據現場測試的地形等高線和設計的工程邊坡要素,建立三維實體模型如圖3所示.

根據實體模型劃分數值計算網格,共離散為71 186個節點和394 323個四面體單元,如圖4所示.

采用位移邊界約束進行計算,四周邊界約束水平方向位移,底部約束豎向位移.

根據勘測資料,研究區基巖裂隙發育,且坡腳開挖對邊坡體有擾動,形成卸荷裂隙,降低巖體強度.因此,綜合確定巖體計算參數:γ=22.0 kN/m3,c=50 kPa,φ=25°,μ=0.30、E=500 MPa.

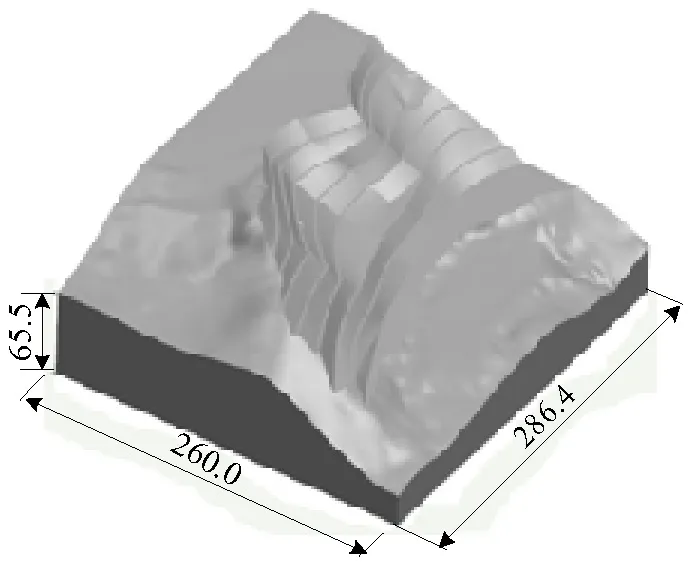
圖3　工程邊坡實體(單位：m)Fig.3　Solid gragh of engineering slope(unit： m)

圖4　計算網格及極限狀態位移云圖Fig.4　Numerical grid and contour map of displacement in limit state

3.2　工程邊坡穩定性

按照本文提出的點安全系數計算步驟,首先計算邊坡處于臨界狀態時的位移場(如圖4).

當折減系數為2.0時,邊坡體位移明顯,最大位移超過了2 000 mm,主軸斷面上位移梯度顯著,能夠明確判斷邊坡的潛在失穩范圍及潛在滑移面.將此臨界狀態的位移場假定為潛在滑動面.

賦予邊坡體實際巖體參數,計算得到邊坡體的當前實際應力狀態.結合臨界位移場計算結果,可計算邊坡的點安全系數,如圖5所示.

從圖5可知:坡體的坡腳處較為危險(圖中橙、紅色部分,點安全系數小于1.30);在邊坡高度方向上,僅下部兩級邊坡點安全系數小于設計安全系數1.35,其縱向高度約17 m,垂直坡面方向上,厚度約7.6 m(圖5(b));從全域圖的橫向上來看,絕大部分走向范圍內的坡腳處均出現了點安全系數小于1.35的區域,且形成了連續片狀;(圖5(c))揭示了小于 1.3的區域位于等值面上部,與邊坡走向近于平行.

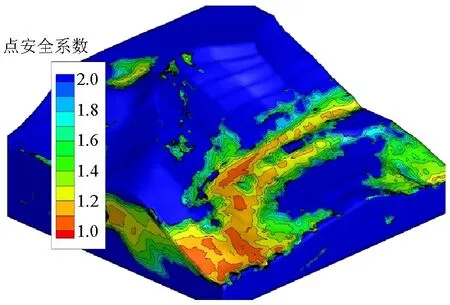
(a) 邊坡全域

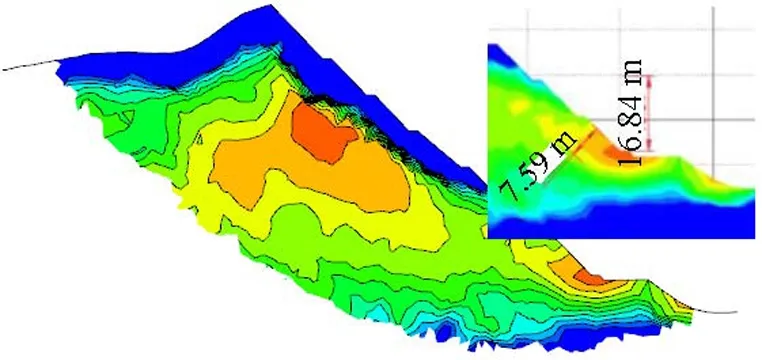
(b) 典型斷面

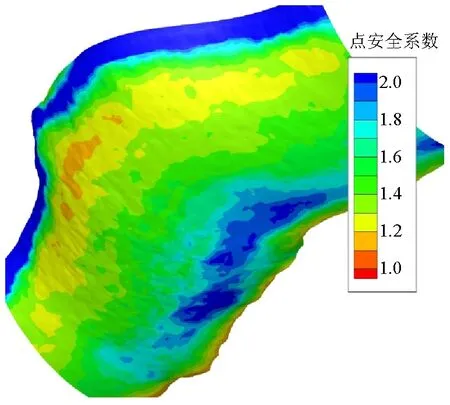
(c) 120 mm等值面圖5　邊坡點安全系數分布Fig.1　Distribution of point safety factor of slope

若僅從整體安全系數上來看，邊坡整體安全系數為1.54，大于設計安全系數(1.35)，可以認為邊坡是安全的.但是從點安全系數來看，若坡體點安全系數小于1.35，說明該部位不滿足設計安全系數，在后期的運營過程中，有可能出現局部破壞，進而導致邊坡漸進破壞而失穩.也就是說，坡體的局部破壞，會逐步降低邊坡的整體穩定性，最終導致邊坡失穩破壞.因此，為確保邊坡工程的運營安全，不僅需要整體穩定性滿足設計要求，邊坡的局部安全性也不能忽視.

基于上述點安全系數計算分析,有必要對局部穩定性較小的坡腳進行錨桿加固.

3.3　加固邊坡穩定性

根據工程邊坡的點安全系數分布特征,擬定錨桿加固方案.其中錨桿的長度以穿過點安全系數小于1.35的區域為目標,錨桿數量及直徑則通過試算確定,以邊坡點安全系數大于1.35為目標.

確定出邊坡的局部加固的范圍為下部兩級邊坡,加固深度為坡面以下8 m范圍內.考慮錨固段為4 m,確定錨桿的長度為12 m.錨桿縱橫向間距分別取3.0、2.0 m和1.0 m,錨桿直徑分別取25、28 mm和32 mm,進行了比較分析.

綜上所述當錨桿間距為2.0 m,錨桿直徑為25 mm時,邊坡局部穩定性問題即可得到顯著改善,點安全系數計算結果如圖6所示.可見,除邊坡坡腳部位有局部區域點安全系數為1.3～1.50之外,邊坡其余部位點安全系數均大于2.0,滿足設計要求,可以確保邊坡穩定安全.

圖6　加固后邊坡點安全系數Fig.6　Point safety factor of reinforced slope

4　結束語

對于復雜空間形態的邊坡體,其應力狀態具有空間差異性,難以采用二維方法進行穩定性分析.本文在邊坡三維點安全系數定義的基礎上,提出了采用FLAC3D軟件進行狀態分析的實施方法，建立了精細的三維數值分析模型,計算了工程邊坡的點安全系數，得到如下結論：邊坡坡腳處較為危險,點安全系數小于1.30.邊坡高度方向上,下部兩級邊坡點安全系數小于1.35,縱向高度約17 m,垂直坡面方向上,厚度約為7.6 m，坡腳處點安全系數小于1.35的區域形成了連續片狀，據此認為,坡腳局部穩定性不滿足設計要求,在后期的運營過程中,有可能出現局部破壞,進而導致邊坡漸進破壞而失穩，需要對坡腳進行錨桿加固，采用錨桿間距2.0 m,錨桿直徑25 mm,加固后,邊坡局部穩定性問題得到顯著改善,點安全系數均大于1.35,滿足設計要求,可以確保邊坡穩定安全.