基于NAM的擴展多功能電壓模式雙二階濾波器合成

阮能海

（南京師范大學 物理科學與技術學院，江蘇 南京 210023）

0 引 言

在能夠利用相同拓撲同時實現多個基本濾波器函數的前提下，后續的研究致力于實現多功能濾波器。文獻[1-7]中提出了許多多輸入端/多輸出端的多功能濾波器，但大多數文獻僅設計了一種新穎電路而很少關注通過系統的方式設計多功能濾波器。

新近文獻[8-12]提出了一種在不需要任何詳細電路形式的先驗知識前提下，實現線性有源電路系統合成的符號化框架，叫作NAM擴展方法，其對系統生成各種新穎的電路非常有效。基于這種有源網絡的合成方法，文獻[13-16]實現了幾種振蕩器、跨阻抗、電流模式和電壓模式濾波器的設計。文獻[9]中提出的電壓模式濾波器的合成過程，適用于合成具有不同電路拓撲的不連續傳遞函數，而使用相同的拓撲卻很難實現合成多個濾波器功能。文獻[17]中報道了使用NAM擴展來簡化電流模式多功能濾波器的系統合成方法。然而，推導多功能濾波器的系統構造方法目前還未見報道。

本文展現了提出的用于合成NAM擴展的多功能電壓模式雙二階濾波器方法的擴展工作，獲得的具有兩個輸入端和三個輸出端的濾波器可以用來實現四個通用的濾波器函數。它們包括四個具有低有源和無源的靈敏度特性的有源元件，并通過HSPICE仿真了八個派生的濾波器來進行驗證說明。仿真結果證實了所得電路的性能，說明了該方法的可行性。

1 提出方法的描述

為了使用NAM擴展來合成濾波電路，傳遞函數的分母D(s)在NAM方程式中應表示為導納矩陣，即：

該矩陣可用作NAM擴展中的起始矩陣，用來找到無輸入端信號的電路配置。可以看出，運用符號化分析后，電壓模式電路的導納矩陣為歸一化導納矩陣，其中節點1為輸入端節點，其他節點為輸出端節點[18]。此外，導納矩陣還包含傳遞函數分子的導納項。由于輸入端電壓源可通過其相同電路（如圖1所示）來表示，所以嘗試將電壓源相同電路連接到合成電壓模式濾波器來擴展式（1）所表示的合成電路的起始NAM。

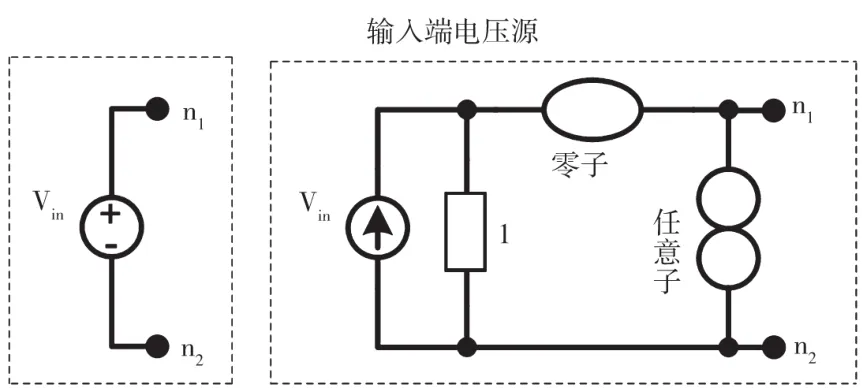
圖1 輸入端電壓源的電阻-零極子相同電路

應該注意到，在NAM擴展過程中，零極子（nullor）-鏡結構對是在合成程序完成后[17]通過四種類型第二代電流傳輸器（Second Generation Current Conveyor，CCII）實現的。所以，憑借合成電路的CCII的電流的以下屬性實現電壓模式濾波器。

CCII通過圖2～圖14所示的零極子-鏡元件[19-20]的無窮變量模型來描述，而這種模型可用于NAM擴展過程[20]。

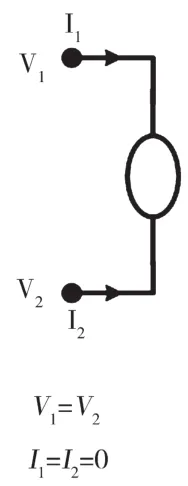
圖2 零子（nullator）的符號和定義

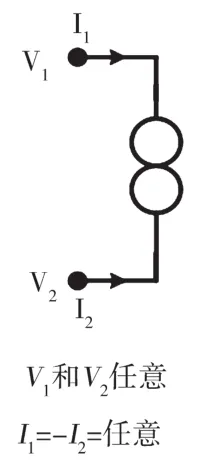
圖3 任意子（norator）的符號和定義

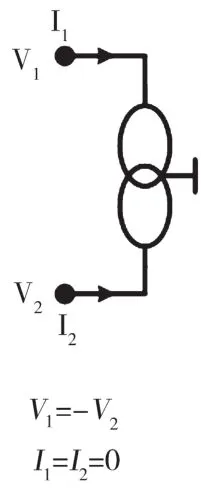
圖4 電壓鏡（voltage mirror）的符號和定義

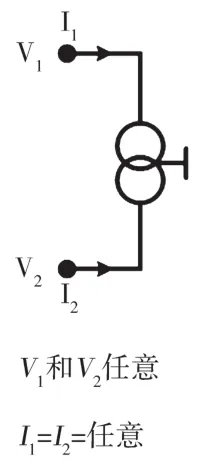
圖5 電流鏡（current mirror）的符號和定義

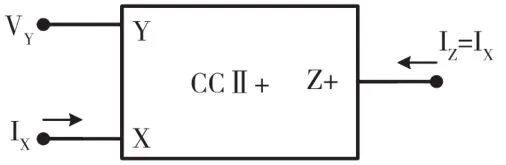
圖6 CCⅡ+符號

圖8 CCⅡ-符號

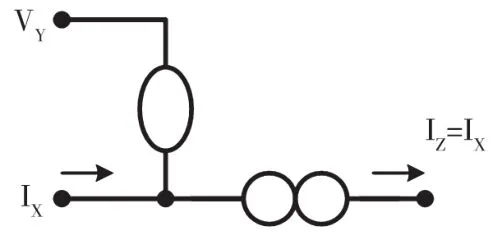
圖9 CCⅡ-（零子-任意子）

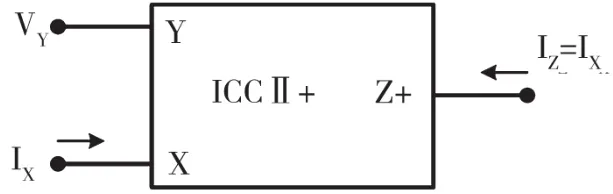
圖10 ICCⅡ+符號

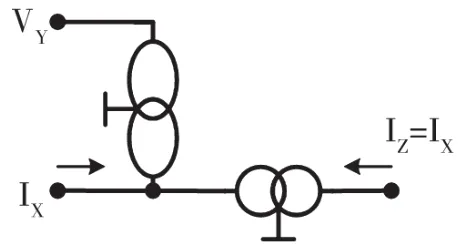
圖11 ICCⅡ+（電壓鏡-電流鏡）

圖12 ICCⅡ-符號

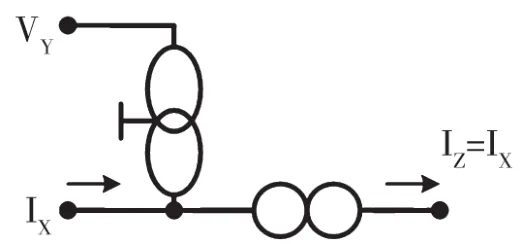
圖13 ICCⅡ-（電壓鏡-任意子）

圖14 CCIIs的NAM表示

電壓模式濾波器的合成程序總結如下。

第1步：將一行和一列零引入到第1行和第1列，將單一電阻放入到矩陣（1）的位置（1，1）。將現有的列和行挪動到右側和底部，如矩陣（2）所示：

第2步：使用克萊姆規則，將出現的導納項添加到矩陣（2）的第一列，以估計所需傳遞函數的分子。必須指出的是，分母中的每個電容器必須排列成在主對角線上只有一個位置，以獲得具有接地電容器的電路。這一操作相同于將輸入端電壓信號連接列1中添加的導納項。導納條件加到第一列不會影響傳遞函數的分母。比如。按照第2步通過添加項±y11可得到矩陣（3）：

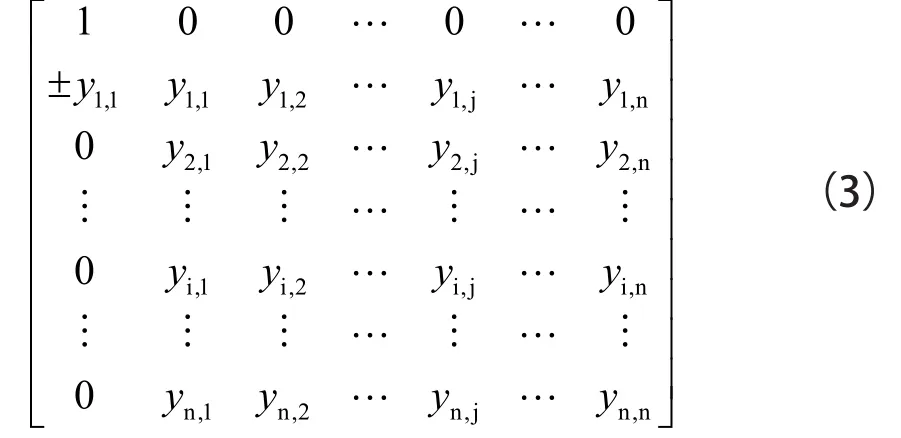
第3步：將一列和一行零項引入到矩陣（3）的第2列和第2行，后來將無窮變量放入到導納矩陣，以實現在圖1[18]中電壓源的相同電路。所以，在第1列和第2列之間引入一個零子，在第2行和接地之間引入一個任意子，則矩陣（3）成為矩陣（4）：

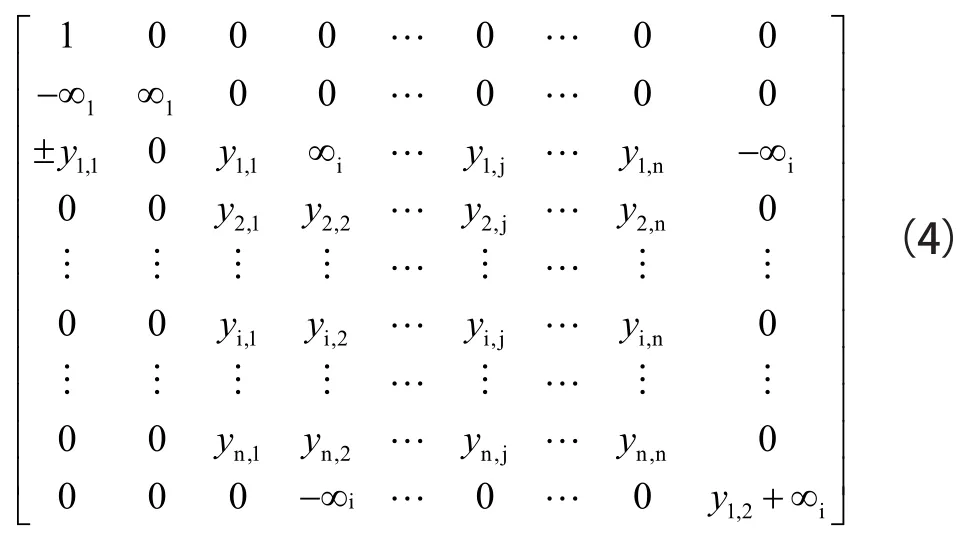
第4步：擴展得到的矩陣（4），找到合成電壓模式電路[19]的完整導納矩陣。

使用四種類型CCII來實現得到電路中的零極子-鏡結構對，計算通過零極子鏡對的每個節點的電流[19]。

2 應用實例

使用最小數量的無源元件來合成電壓型多功能雙二階濾波器。電壓模式多功能雙二階濾波器的傳遞函數的分母選為方程（5），即：

每個電容排列成在NAM的主對角線上只有一個位置，可得到具有接地電容的幾個濾波器函數。方程式（5）由矩陣（6）按照第1步的程序，以矩陣（1）的形式表示。按照第1步的程序，可以通過矩陣（6）得到相同NAM，即矩陣（7）：

從矩陣（7）出發，它們可以在NAM擴展中用作起始矩陣。節點1選為輸入端節點，節點2、節點3和節點4都是輸出端節點。

運用第2步，通過將輸入端電壓源連接到R1=1/G1，可在VO1是一個帶通函數，在VO2是一個低通函數，在VO3是一個高通函數。此操作對應插入項-G1到矩陣（7）的第一列，即：

運用第3步可得到矩陣（9）：

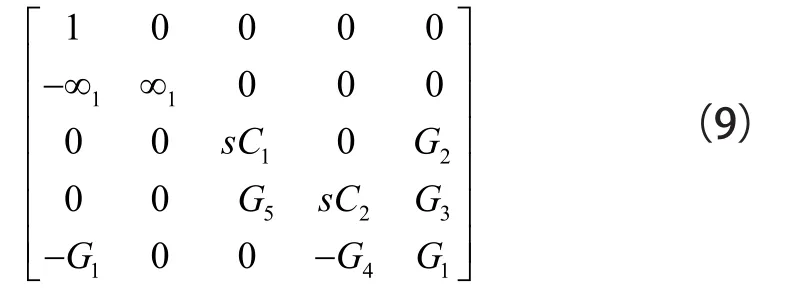
通過項±∞1，可以將項-G1挪動到第2列，將元件±G1添加到第2行，以完成項G1的對稱元件集，如矩陣（10）所示：

通過運用第4步添加零項的四列，行、零極子-鏡元件（由∞2，∞3，∞4和∞5表示）介紹到矩陣（10）的右側和底部。所以，矩陣（10）可擴展為矩陣（11）：

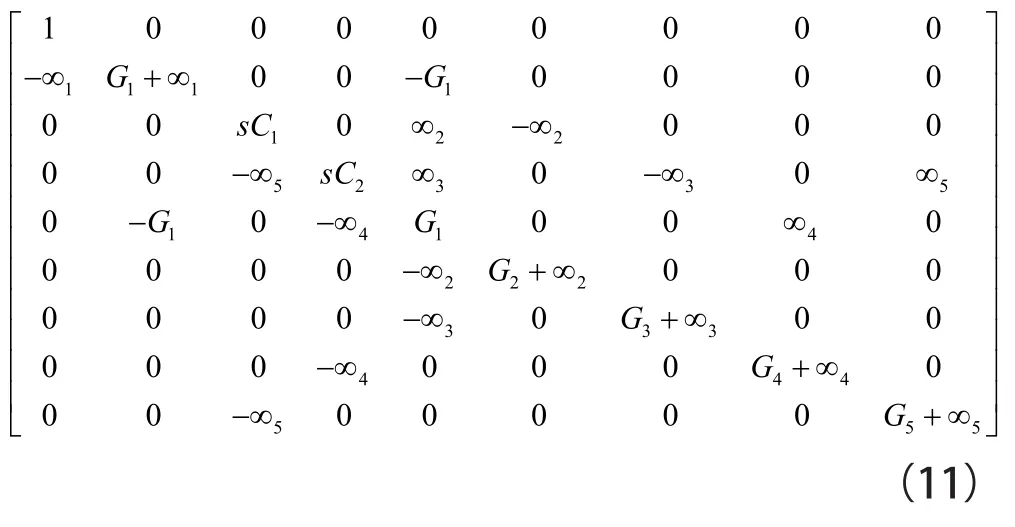
得到的由（11）表示的濾波器，如圖15（挑選4）所示。其中，Vi2節點接地。有八種替代挑選1～挑選8可通過擴展矩陣（9）來引入各個零極子-鏡元件對。每個合成電路包括4個有源元件、7個無源元件和2個接地電容，如圖16～圖23所示。

由矩陣（11）表示的電路濾波器，如圖15所示，連接到輸入端節點Vi1和輸入端節點Vi2的電壓源的輸出端接地。有8個替代挑選可以通過擴展（10）來引入各個無窮變量，如圖16～圖23所示。圖16～圖23中，由矩陣表示的電路濾波器使用的是零極子-鏡對。已知圖16～圖23中的每個構造對有一個公共端，因此可以通過正確的電流傳輸器來實現。

圖15 提出的使用電流傳輸器的高通、低通和帶通電壓模式濾波器

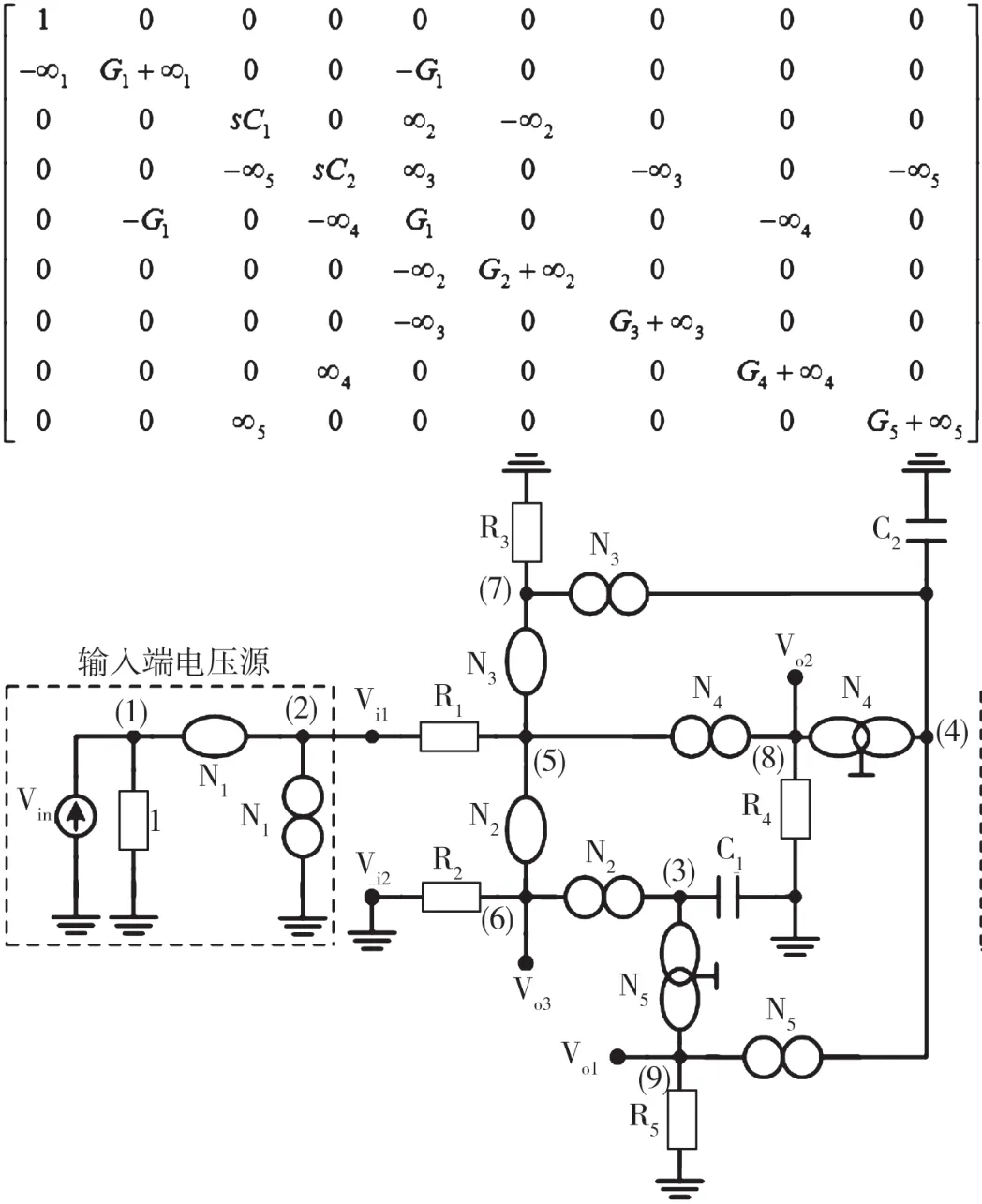
圖16 挑選1

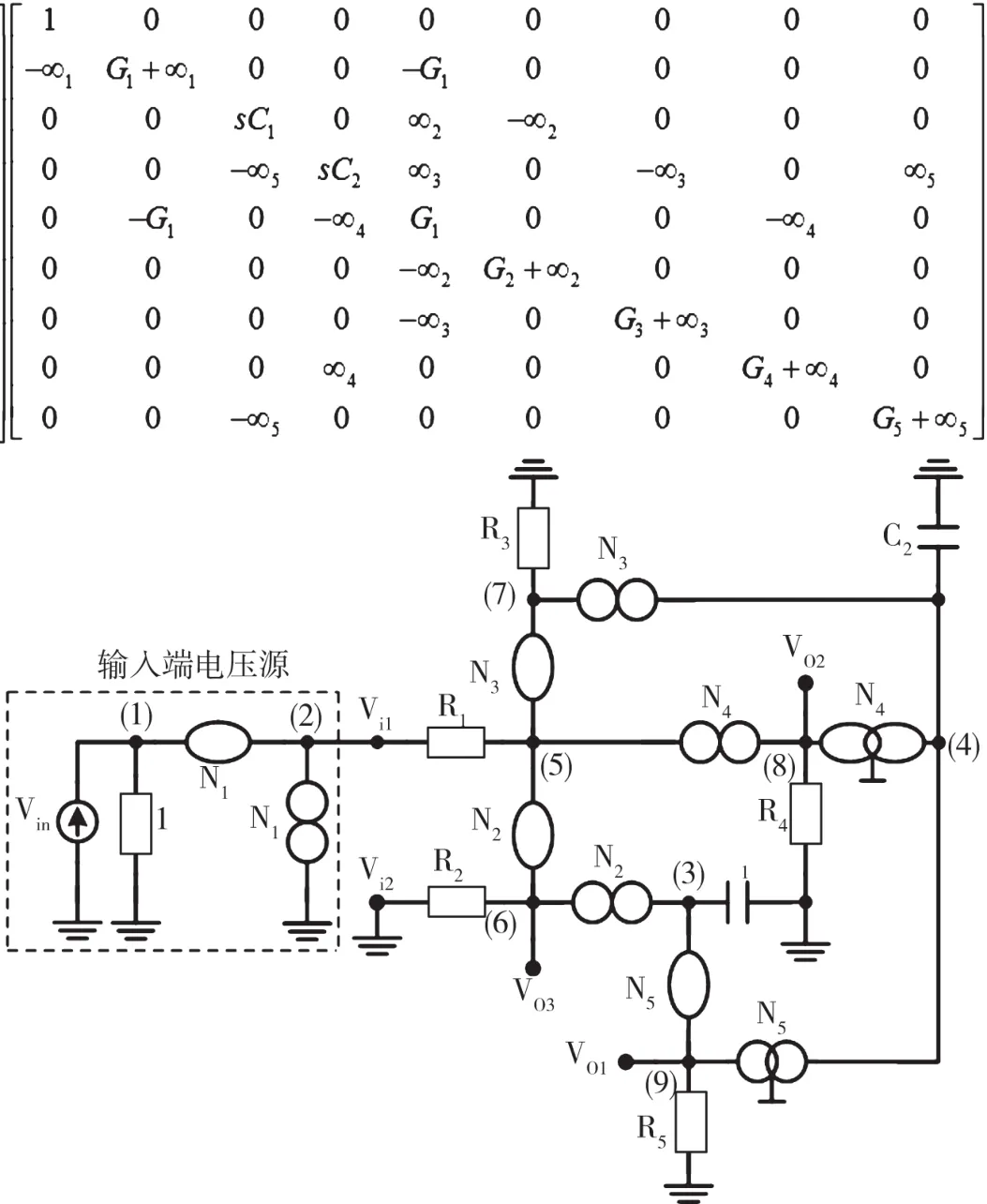
圖17 挑選2

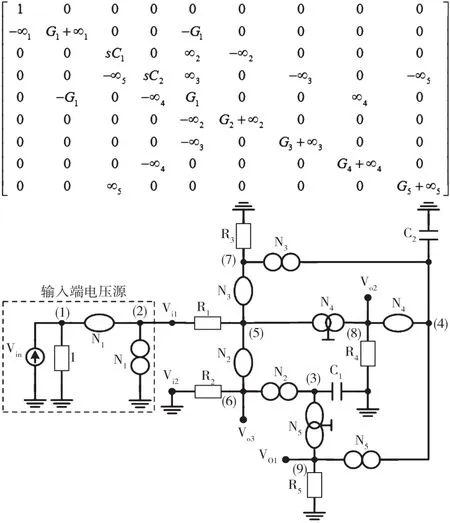
圖18 挑選3

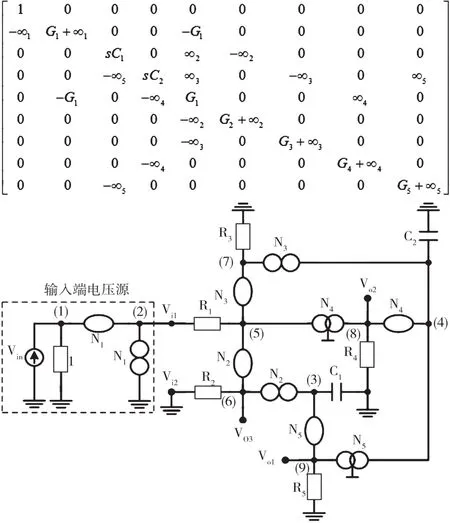
圖19 挑選4

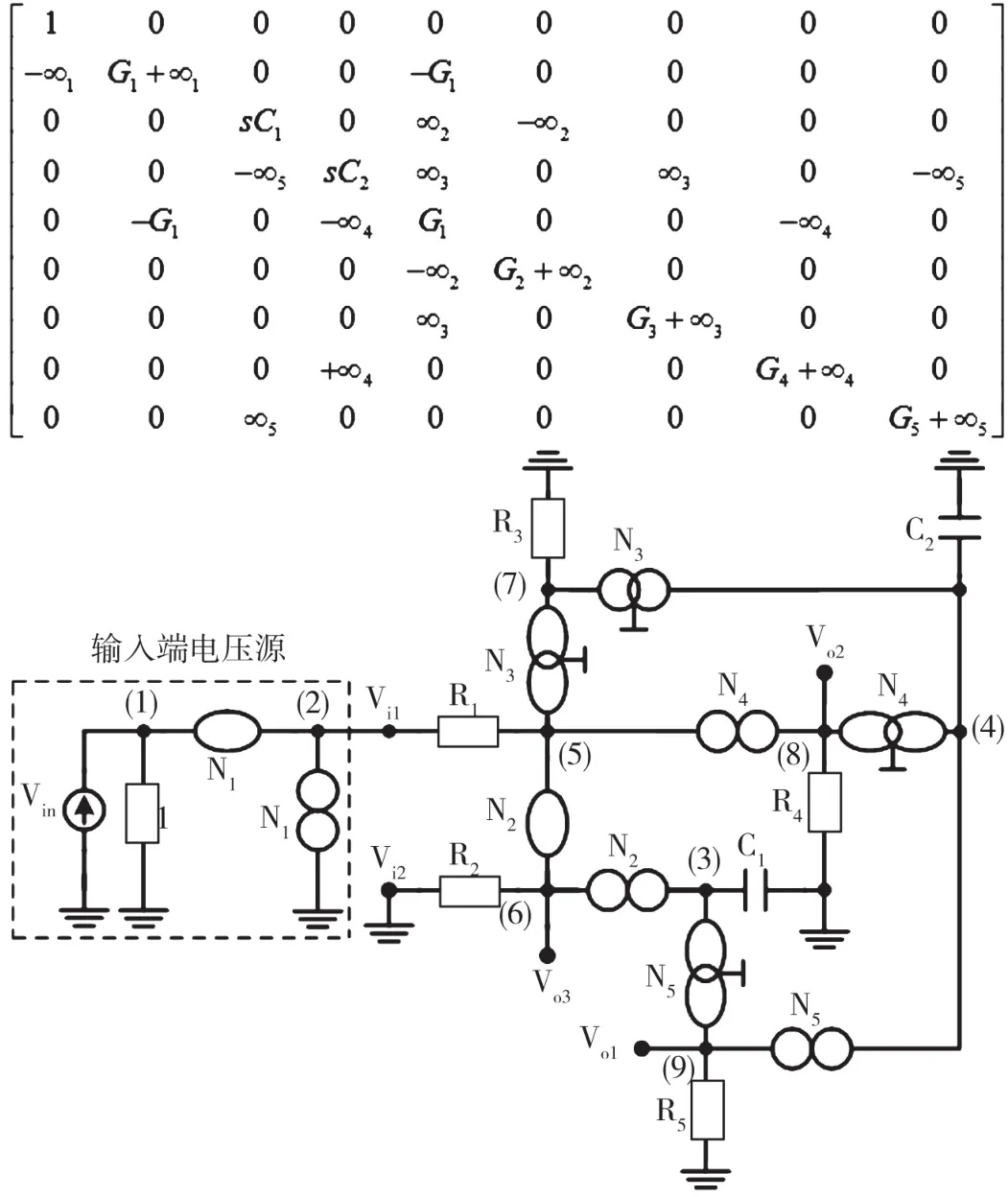
圖20 挑選5

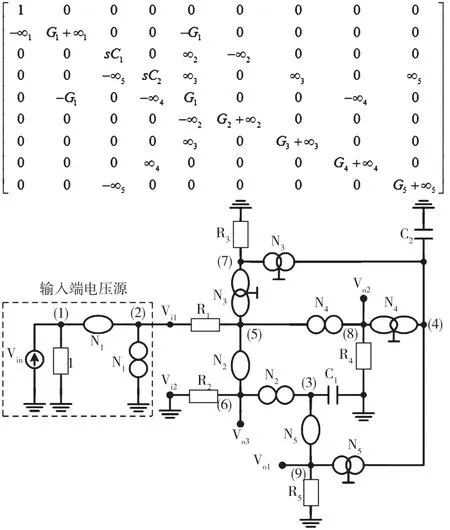
圖21 挑選6

圖22 挑選7

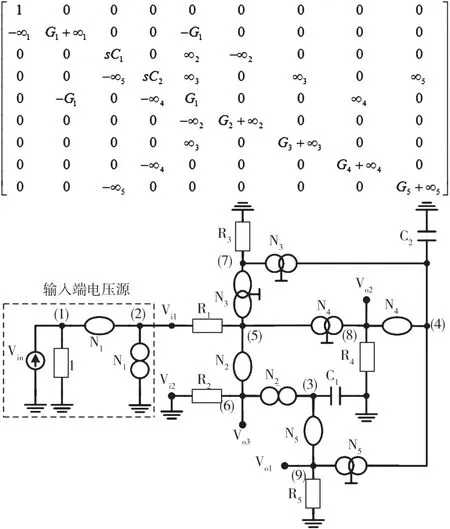
圖23 挑選8

同樣，通過將輸入端電壓源連接到R2=1/G2，可在Vo1、Vo2和Vo3都是低通函數。該操作相同于將項-G2插入到矩陣（7）的第一列，如矩陣（12）所示：

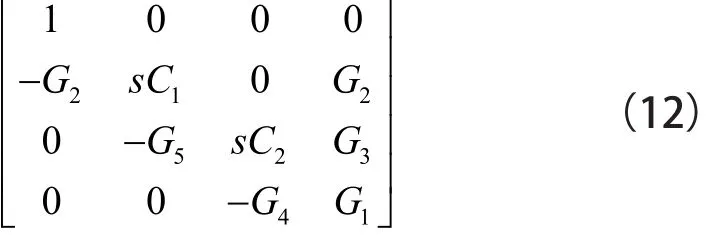
應用第3步和第4步引入零極子-鏡對（由∞1，∞2，∞3，∞4，∞5表示），矩陣（12）可擴展為矩陣（13），即：

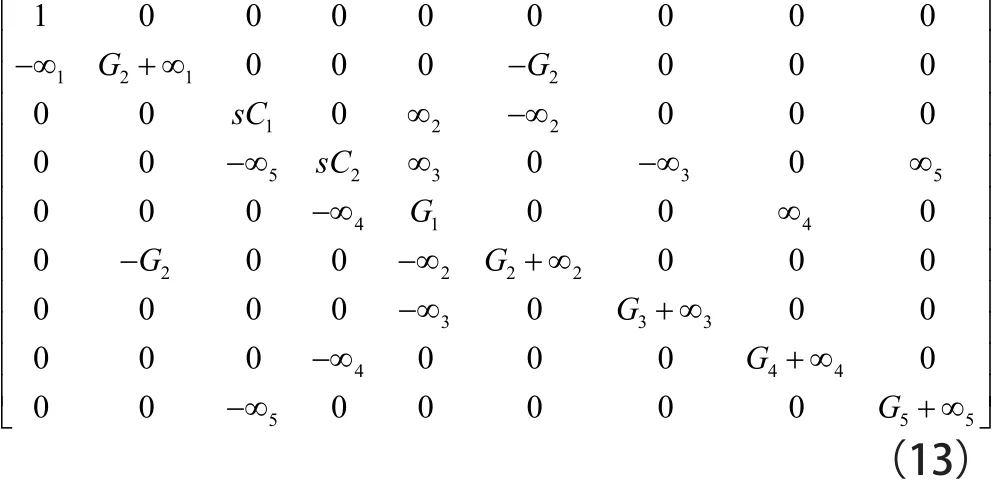
對于圖24中的電路，挪動相同電路電壓源的輸出端、輸入端節點Vi2和輸入端節點Vi1接地，可得到由矩陣（13）表示的濾波器。

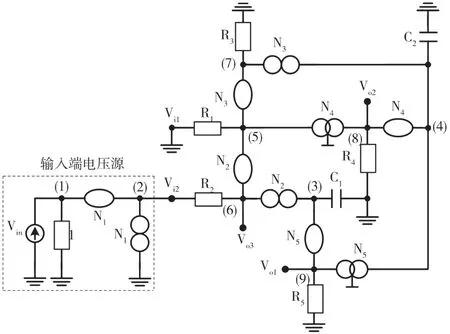
圖24 提出的使用電流傳輸器的低通電壓模式濾波器

通過將輸入端電壓源連接到R1和R2，可在Vo1是一個低通函數，在Vo2是一個帶通函數，在Vo3是一個陷波函數。該操作相同于將項-G1和項-G2插入到矩陣（7）的第一列，如矩陣（14）：

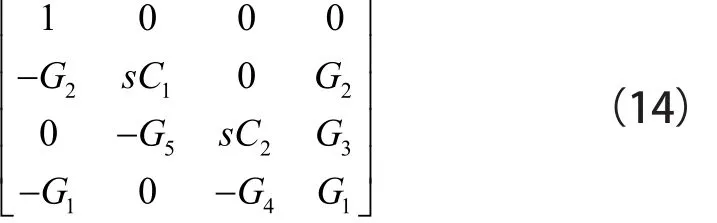
應用第3步和第4步引入零極子-鏡對（由∞1，∞2，∞3，∞4，∞5表示），矩陣（14）可擴展為矩陣（15），即：

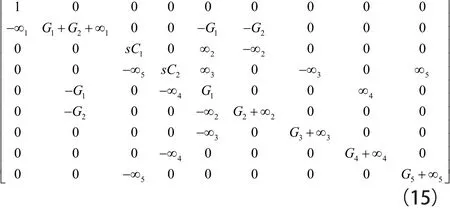
對于圖25中的電路，將相同電路電壓的源輸出端挪動到輸入端節點Vi1和Vi2，可得到由矩陣（15）表示的濾波器。

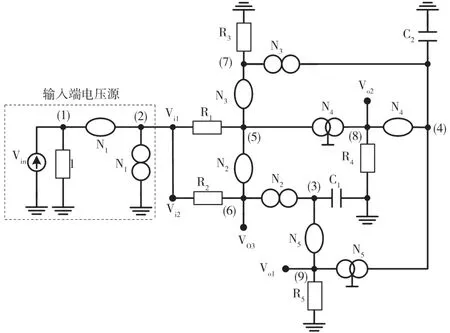
圖25 提出的使用電流傳輸器的陷波、帶通和低通電壓模式濾波器

電壓模式帶通、低通、高通和陷波濾波電路的所有上述合成的傳遞函數，可通過式（16）、式（17）、式（18）表示[18]。圖26顯示了實現圖15、圖25和圖26中結構相同的實際組態。在表1中和圖26濾波電路中使用電流傳輸器，提議的網絡、基于并使用±類型的CCII±所提出的網絡如圖26所示。使用標準符號、CCII±的端口關系可以通過圖6～圖14、vx=vy,iz=±ix和iy=0來描述。

圖26 電壓模式多功能雙二階濾波器結構的實現

容易得到，可正交調整每個提出網絡的諧振角頻率ω0和極點品質因數Q：

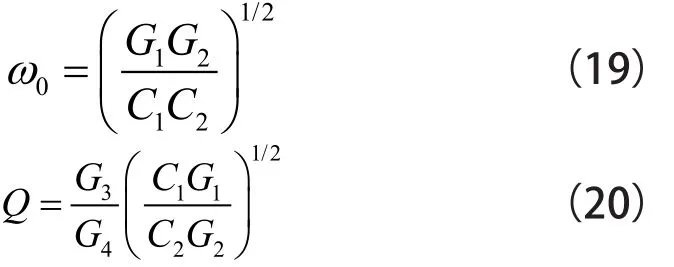
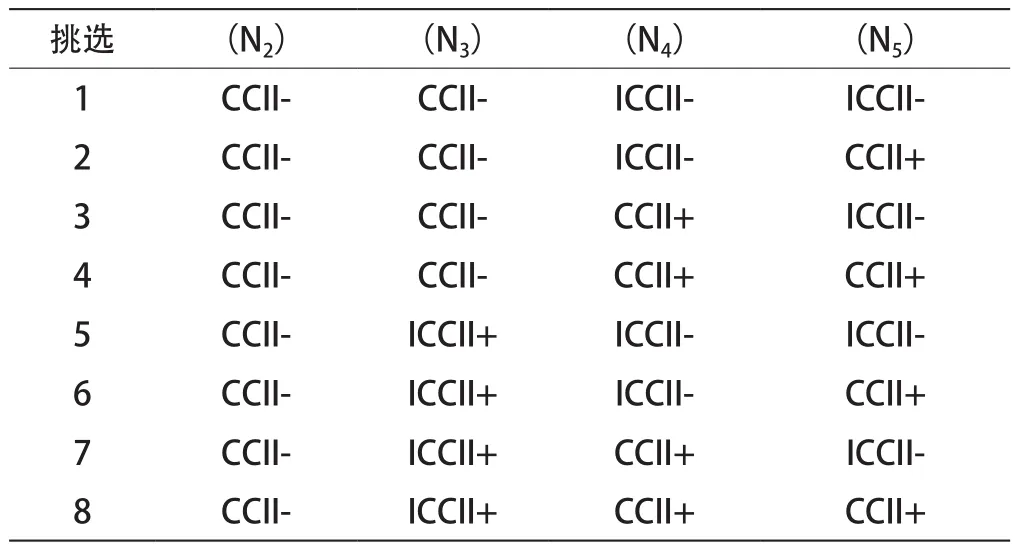
表1 使用電流傳輸器的電壓模式多功能雙二階濾波器

3 得到的基于CCII的電壓模式多功能雙二階濾波器的仿真結果

為了驗證提出方法的可操作性，對圖27中得到的濾波器使用TSMC 0.35 μm（臺灣積體電路制造股份有限公司）過程參數進行HSPICE模擬，模擬中使用CCII±的CMOS實現，結果如圖28[20]所示。

圖27 電壓模式多功能雙二階濾波器結構的實現

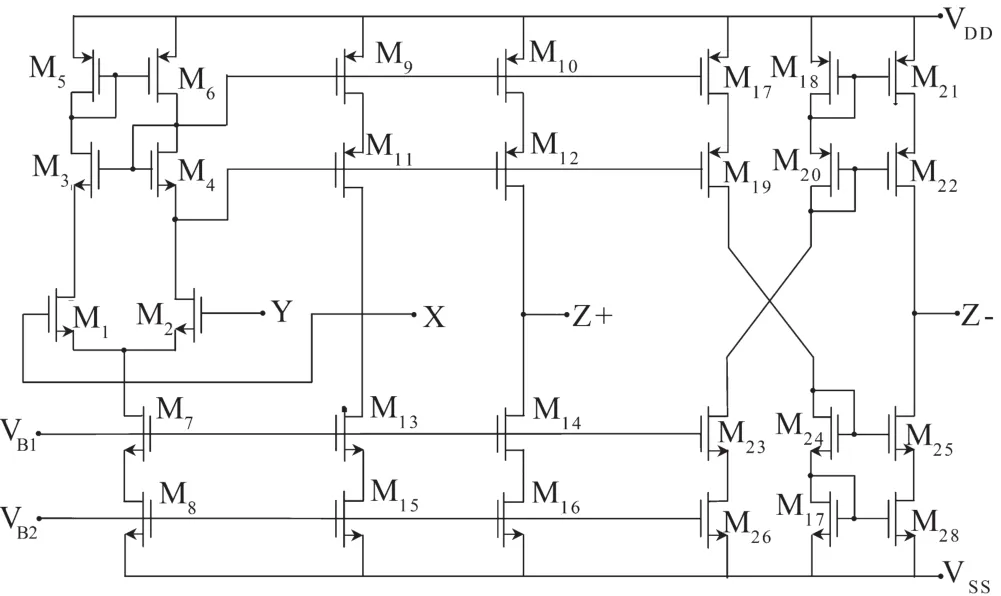
圖28 CCII±的CMOS電路

每個PMOS和NMOS晶體管的長寬比分別為W/L=10μm/1μm 和 W/L=5μm/1μm[21]。CCII±的電源電壓是VDD=-VSS=1.5 V、偏壓電壓是VB1=-0.52 V和VB2=-0.33 V。對于圖28中的模擬多功能雙二階濾波器，使用的有源元件是N2（CCⅡ-）、N3（CCⅡ-）、N4（CCⅡ+）、N5（CCⅡ +），無源元件值是C1=C2=1 nF和R1=R2=R3=R4=R5=10 kΩ。模擬結果如圖29所示。

4 結 論

本文中提出了一種用于合成多功能電壓模式雙二階濾波器的系統合成過程。提出的方法以使用零鏡面結構元件的NAM展開方法為基礎，獲得了具有2個輸入端節點、3個輸出端節點的濾波器，可以實現全部的,4個通用函數。HSPICE模擬結果顯示，合成電路具有有效性，從而驗證了所提方法的可行性。

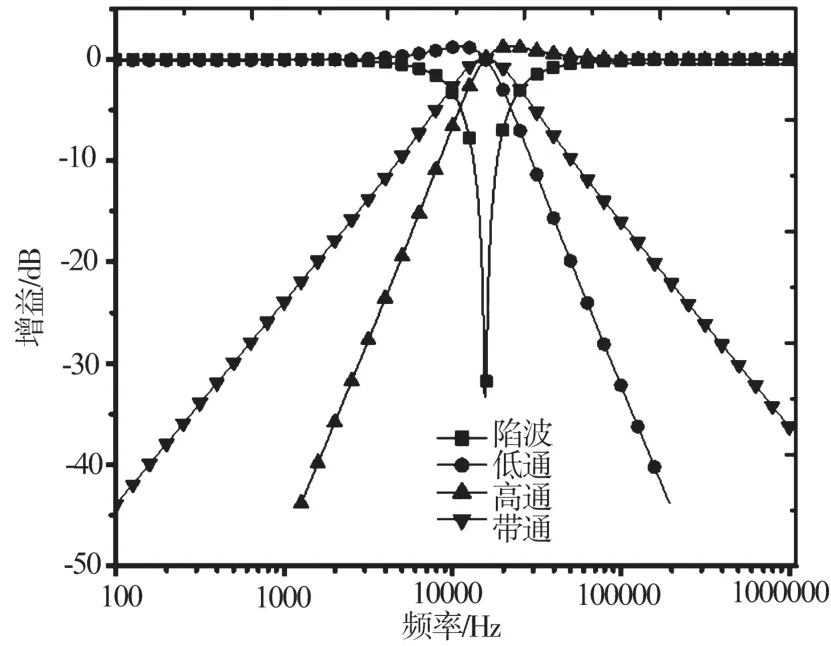
圖29 多功能雙二階濾波器的頻率響應

[1] 李永安，曹暋蕤.基于CCIIs接地回轉器的系統綜合法[J].電子設計工程，2017，25（3）：72-75.

[2] Jiun-Wei H. High-input Impedance Voltage-mode Universal Biquadratic Filters with Three Inputs Using Plus-type CCIIs[J].Int. J. Electron，2004，（91）：465-475.

[3] Jiun-Wei H.High-input Impedance Voltage-mode Universal Biquadratic Filters Using Three Plus-type CCIIs[J].IEEE Trans. Circuits Syst，2001（48）：996-997.

[4] CHANG Chun-ming，TU Shu-hui.Universal Voltage Mode Filter with Four Inputs and One Output Using two CCII+s[J].Int. J. Electron，1999，（86）：305-309.

[5] Tarim N，Kuntman H.The Effects of CCII Nonidealities on Voltage-Mode Active Filters[J].Microelectronics Journal，1999，（30）：1265-1272.

[6] Chang C M，Al-Hashimi B M，Ross J N.Unified Active Filter Biquad Structures[J].IEE Proceedings-Circuits，Devices and Systems，2004，151（4）：273-277.

[7] WANG Hung-Yu，Ching-Ting L.Versatile Insensitive Current-mode Universal Biquad Implementation Using Current Conveyors[J].IEEE Transactions on Circuits and Systems II，2001，48（4）：409-413.

[8] David G H，Thomas J W C，Paul M R.Symbolic Framework for Linear Active Circuits Based on Port Equivalence Using Limit Variables[J].IEEE Transactions on Circuits and Systems，2006，53（9）：2011-2024.

[9] David G H.A Method of Transformation from Symbolic Transfer Function to Active-RC Circuit by Admittance Matrix Expansion[J].IEEE Trans Circuits Syst I：Regul Pap，2006，53（12）：2715-2728.

[10] Haigh D G，Tan F Q，Papavassiliou F.Systematic Synthesis of Active-RC Circuit Building-Blocks[J].Analog Integrated Circuits and Signal Processing，2005：297-315.

[11] David G H，Paul M R.Admittance Matrix Models for the Nullor Using Limit Variables and Their Application to Circuit Design[J].IEEE Transactions on Circuits and Systems，2006，53（10）：2214-2223.

[12] 譚玲玲，滕建輔，劉開華，等.有源RC濾波器網絡的綜合[J].電路與系統學報，2011，16（5）：6.

[13] Yong-An L.On the Systematic Synthesis of OTA-based Wien Oscillators[J].AEU-Int. J. Electron. Commun，2013，（67）：754-760.

[14] Lingling T，Yu B，Jianfu T，et al.Trans-impedance Filter Synthesis Based on Nodal Admittance Matrix Expansion[J].Circuits Systems and Signal Processing，2013,32（3）：1467-1476.

[15] 譚玲玲，滕建輔，劉開華，等.一種基于節點導納矩陣（NAM）擴展理論的浮地電感和浮地FDNR電路的綜合[C].中國電子學會電路與系統學會年會，2011.

[16] Ahmed M S.Two Integrator Loop Filters：Generation Using NAM Expansion and Review[J]. Hindawi Publishing Corporation Journal of Electrical and Computer Engineering，2010：8.

[17] Ahmed M S.Generation of Current Mode Filters Using NAM Expansion[J].Int J Circuit Theory，2011，39（4）：1087-1103. [19]Ahmed M S.On the DVCC and the BOCCII as Adjoint Elements[J].Journal of Circuits，Systems，and Computers，2009，18（6）：1017-1032.

[18] Hung-Yu W，Wen-Chung H，Nan-Hui C.Symbolic Nodal Analysis of Circuits Using Pathological Elements[J].IEEE Transactions on Circuits and Systems II，2010，（57）：874-877.

[19] Samy A S，Ahmed M S.Use of Mirror Elements in the Active Device Synthesis by Admittance Matrix Expansion[J].IEEE Trans Circuits Syst I：Regul Pap，2008，55（9）：2726-2735.

[20] Acar C，Kuntman H.Limitations on input Signal Level in Voltage-mode Active-RC Filters Using Current Conveyors[J].Microelectronics Journal，1999，（30）：69-76.

[21] CHEN Hua-pin.Single CCII-based Voltage-Mode Universal Filter[J].Analog Integr Circ Sig Process,2010，（62）：259-262.[23]INAS A A，AHMED M S.Inverting Second Generation Current Conveyors：The Missing Building Blocks，CMOS Realizations and Applications[J].INT. J. ELECTRONICS，1999，86（4）：413-432.