考慮負荷不確定性的微電網優化調度研究

,,

(1.國家電網公司西南分部，四川 成都 610041；2.電子科技大學，四川 成都 611731)

0 引 言

近年來隨著世界經濟的快速發展，世界各國對能源的需求不斷增大，一方面，造成全球能源供應的日益緊張；另一方面，也帶來了諸如氣候惡化、溫室效應等嚴重的環境問題。因此，提升新能源利用比例、改善能源結構、緩解能源利用與環境保護之間的矛盾，已成為當前能源及電力體系的發展共識和必然趨勢。

微電網(Microgrid)是一種新型的能源網絡化供應與管理結構，由分布式電源、儲能裝置、控制裝置及負荷組成。相對于傳統電網發電系統，微電網可有效實現大規模分布式電源的靈活接入與高效利用，在降低能耗和減少環境污染的同時，也提高了系統的可靠性與靈活性。

隨著微電網技術的不斷成熟，微電網功能和結構日趨復雜，對微電網運行的經濟、環保、可靠性的要求也不斷提高[1]。如何改善提升其運行的經濟性與環保性，已成為當前國內外微電網優化運行的研究熱點。文獻[2]建立了包括建設及折舊費用、維護費用、無功補償成本及政府新能源補貼的經濟性目標，而微電網的環保性通過系統的污染物排放懲罰來衡量；通過基于改進的遺傳算法對優化模型進行求解。文獻[3]將微電網的環保性用環境成本來計算，將其與經濟性目標列入同一個目標函數；其經濟性目標函數考慮了并網時的運行成本、運行維護成本、MT的燃料成本及制冷制熱收益；利用改進的雞群算法對優化模型進行求解。但上述研究僅將微電網環保性改善作為首要前提，未同時考慮運行方式對于微電網經濟性的影響。文獻[4]將經濟成本及CO2的排放量作為調度優化的兩個目標，采用將模糊矩陣引入傳統粒子群算法中的方法，協同優化兩目標。文獻[5]在以運行成本最小為優化目標的基礎上，考慮了風力發電及光伏發電的功率預測存在誤差，通過貝塔分布擬合出有誤差的可再生能源發電功率曲線，研究其誤差大小對微電網穩定經濟運行的影響。但上述研究僅針對固定發電單元進行優化，未考慮多種能源接入的協調問題。

為解決上述問題，搭建了含風力、光伏、燃氣輪機、燃料電池及蓄電池等多供能主體的微電網模型，在綜合考慮能量供需平衡、爬坡速率約束及蓄電池充放電容量限制條件下，運用混合整數規劃優化方法，建立了考慮負荷的不確定性因素下以離網型微電網為主的微電網經濟調度模型，并針對多種典型負荷場景對建立的模型準確性進行了驗證。

1 分布式電源的數學模型

1.1 風機發電模型

風機的發電量由風速決定，已知風速即可求出出力。風機出力與風速的關系可近似表示為

(1)

式中：Pr為風機額定功率；V為風力發電機所受的風速；VO為額定風速；a和b為風機出力曲線的擬合參數，其計算公式為

(2)

式中：VI為切入風速；Vr為切出風速。

1.2 光伏發電模型

光伏發電的發電量由光照強度及環境溫度決定，在標準測試條件下，光伏電池的輸出功率為

PPV=PSTC(GT/GSTC)·[1-k(Tc-Tr)]

(3)

式中：PSTC為標準測試條件(即太陽光照強度1000 Lux，環境溫度25℃時)下的最大測試功率；GT為運行時的光照強度；GSTC為標準測試條件下的光照強度；k為功率溫度系數，取-0.47[6]；Tr為參考溫度；Tc=Te+30·(GT/1 000)，Te為運行時的環境溫度。

1.3 燃料電池模型

燃料電池是一種將燃料和氧化劑中的化學能不經過燃燒直接轉換為電能的裝置，因此燃料電池不受卡諾循環的限制。因其能量轉換效率高、啟動速度快、體積小、污染小等優點，廣泛應用于微電網。燃料成本的計算如式(4)。

CFC=(CM/L)·∑(PFC(t)·Δt/ηFC(t))

(4)

式中：CM為天然氣的市場價格，取2.5元/m3[7]；L為天然氣的低熱值，取9.7 kWh/m3，PFC(t)為t時刻的凈輸出電功率；ηFC(t)為燃料電池的效率。

1.4 燃氣輪機模型

微型燃氣輪機是一種小型的熱動裝置，功率一般在30～250 kW，以天然氣、甲烷、汽油等作為燃料，因其可靠性高、體積小、污染小等優點，使其具有廣泛的商業發展前景，適用于各種環境的微電網。

燃汽輪機的燃料成本計算與燃料電池的相近：

CFC=(CM/L)·∑(PFC(t)·Δt/ηFC(t))

(6)

1.5 蓄電池模型

蓄電池具有電能雙向流動、可兼顧容量和功率需求、優異的環保效益等優勢，蓄電池等儲能裝置在微電網中占據著重要作用。特別是在微電網工作于離網模式時，由于失去了與大電網交互能量的途徑，蓄電池作為既可充電亦可放電的裝置，可暫時替代大電網的部分功能，所以蓄電池在微電網中的應用至關重要。

蓄電池充放電時主要涉及其剩余容量的計算，通過計算其剩余容量，即可知道何時能充電或放電，以及充放電電量。蓄電池t時刻的剩余容量，與前一時刻的剩余電量及充放電量相關，計及蓄電池的自放電率與充放電效率，其剩余容量計算公式如下[8]。

放電時,P(t)>0:

(6)

充電時，P(t)<0:

SOC(t)=SOC(t-1)(1-δ)-PSB(t)ηSB

(7)

式中：SOC(t)為蓄電池t時刻的容量；δ為蓄電池的自放電率；PSB為蓄電池t時刻的充放電量；ηSB為蓄電池的充放電效率。

通過建立各分布式電源發電功率的數學求解模型，即可根據現有的可測量的數據求解分布式電源的發電功率。進而通過建立微電網的優化調度模型，可優化各分布式電源的出力情況。

2 微電網的優化模型

2.1 目標函數

下面將綜合考慮到微電網運行的經濟性與環保性，且微電網處于離網模式下的優化模型，不考慮微電網與外網交互的成本。目標函數可分為經濟性與環保性。

1)經濟性

考慮微電網一天內的發電成本最低，其中發電成本包括燃料成本、投資折舊成本、運行維護成本。其目標函數表達式為

f(t)=f1(t)+f2(t)+f3(t)

(8)

式中，f1(t)為燃料成本，其計算公式為

f1(t)=CFC+CMT

(9)

式中，CFC、CMT分別為燃料電池及微型燃氣輪機的燃料成本。

f2(t)為設備投資折舊成本，其計算公式可表示為[9]

(10)

式中，Pi(t)為第i個分布式電源的在t時刻的出力；CAZ,i為第i個分布式電源的單位容量安裝成本；ki為第i個分布式電源的容量因數；r為年利率；q為第i個分布式電源投資回收年限。

f3(t)為設備運行維護成本，其計算公式可表示為[10]

(11)

式中，KWH,i為第i個分布式電源的單位電量運行維護成本系數。

2)環保性

通過將分布式電源排放的污染物的量，轉化為其因排放污染物所需付出的環境保護成本來計算。

(12)

式中，M為排放的氣體的種類總數；CHB(m)為每種排放的氣體對應的環保治理費用；kmi為第i個設備排放第m種氣體時的排放因子。

2.2 約束條件

1)功率平衡約束

任意時刻各分布式電源的出力之和需滿足微電網的負荷需求。

(13)

2)各分布式電源的出力約束

任意時刻分布式電源的出力不能超出自身最大、最小功率的限制[15]。

Pi(t)min≤Pi(t)≤Pi(t)max

(14)

式中，Pi(t)min與Pi(t)max分別為第i個分布式電源出力的最大值與最小值。

3)MT的爬速率約束

增出力時，有：

PMT(t)-PMT(t-1)≤Pup,MT

(15)

前后兩個調度時間的出力之差應小于其爬坡速率。

減出力時，有：

PMT(t-1)-PMT(t)≤Pdown,MT

(16)

式中，Pup,MT、Pdown,MT分別為微型燃氣輪機增出力和減出力時單位時間內的變化功率限制。

4)蓄電池的相關約束

蓄電池在充電或者放電時，每次充放電的電量有所限制；其充放電后，蓄電池的容量要保持在限值之內；在一天的調度周期內，蓄電池的始末容量需保持相同。

所建立的蓄電池充電模型，選擇了最大輸出功率為100 kW,單位時間內的輸出功率不超過最大輸出功率的20%。其表達式為

(17)

式中：P+為蓄電池放電時的功率；P-為蓄電池充電時的功率；PSB,max為蓄電池的最大輸出功率。

蓄電池總的容量還需要控制在一定范圍內。在蓄電池充電的時候，其充電后的最大容量不能超過其自身的最大容量。蓄電池在放電的時候，如果放電深度過大，會降低蓄電池的使用壽命，所以需限制放電后最小剩余容量，即將其規定為放電后蓄電池的容量不小于最大容量的20%。其數學表達式為

SOCSB,max(t)·20%≤SOCSB(t)≤SOCSB,max(t)

(18)

式中：SOCSB,max(t)為蓄電池充放電時可以充放電容量的最大值；SOCSB(t)為t時刻蓄電池的容量值。

為滿足蓄電池循環調度的前提，蓄電池在一個周期的充放電電量需滿足始末平衡。即可表示為蓄電池在一個調度周期內充放電電量相同：

∑SOCSBC=∑SOCSBF

(19)

蓄電池可以工作于充電、放電兩種狀態下，為求解模型方便，引入狀態開關變量Oc(t)、Of(t)來表示蓄電池在t時刻的充放電狀態。在t時刻，Oc(t)值為1則表示充電，Of(t)值為1則表示放電。則式(17)、式(18)、式(19)可表示為

(20)

式中，

Oc(t)+Of(t)=1

(21)

在蓄電池參與優化調度時，如頻繁地轉換蓄電池的充放電狀態，也會導致蓄電池的使用壽命變短。為延長蓄電池的使用壽命，還需對蓄電池的充放電次數進行限制，故引入狀態變量NSB(t)，對其進行如下定義：

NSB(t)=|Oc(t)-Oc(t-1)|

(22)

式中，Oc(t-1)為蓄電池上一個調度時間的開關變量狀態值。蓄電池在一個調度周期內充放電次數的約束條件可表示為

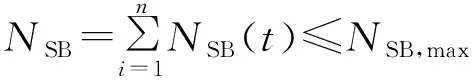
(23)

式中，NSB,max為蓄電池一個調度周期內最大的充放電轉換次數。

3 算例及分析

3.1 微電網系統結構

采用 9節點的輻射狀的微電網驗證所建模型，在滿足系統約束條件下實現微電網能量優化分配。微電網結構如圖1所示。考慮微電網負載容量，設置風電單元容量、光伏單元容量、微型燃氣輪機單元容量、燃料電池單元容量及儲能單元容量分別為20 kW、12 kW、65 kW、40 kW、120 kW。

3.2 模型參數

5個負荷曲線示意如圖2所示。

主要各分布式電源單元參數設置見表1。

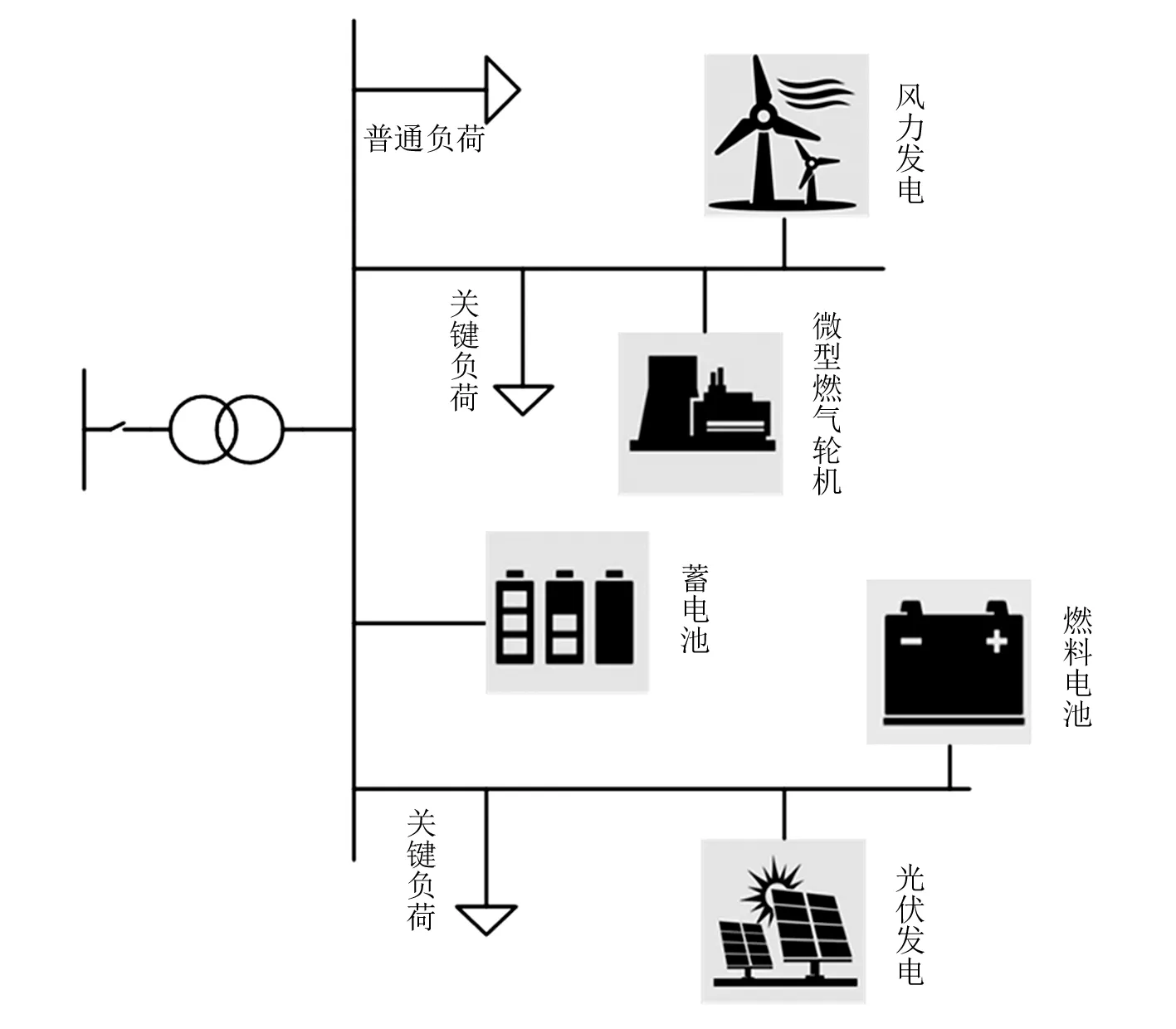
圖1 微電網結構

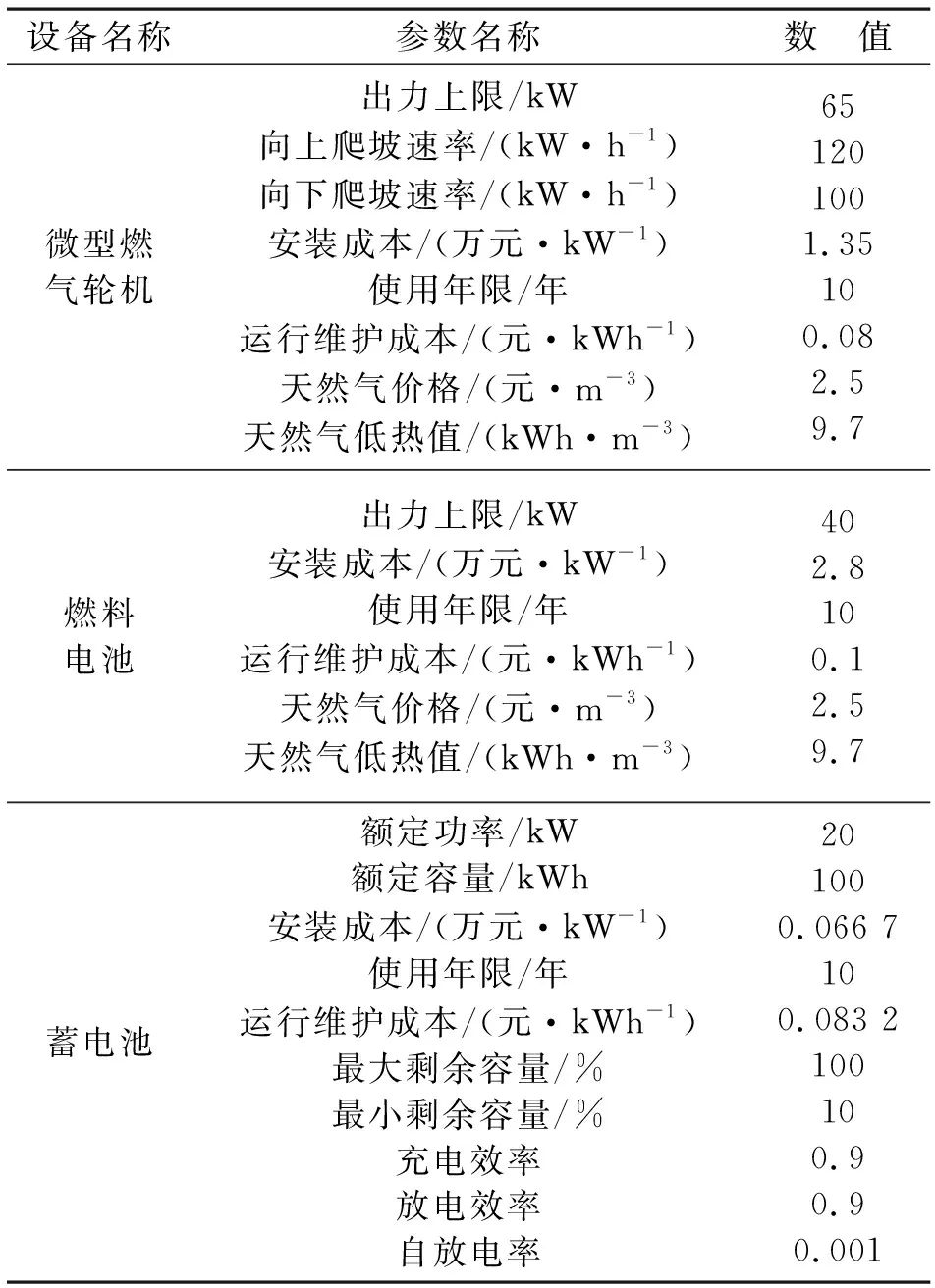
設備名稱參數名稱數 值微型燃氣輪機出力上限/kW向上爬坡速率/(kW·h-1)向下爬坡速率/(kW·h-1)安裝成本/(萬元·kW-1)使用年限/年運行維護成本/(元·kWh-1)天然氣價格/(元·m-3)天然氣低熱值/(kWh·m-3)651201001.35100.082.59.7燃料電池出力上限/kW安裝成本/(萬元·kW-1)使用年限/年運行維護成本/(元·kWh-1)天然氣價格/(元·m-3)天然氣低熱值/(kWh·m-3)402.8100.12.59.7蓄電池額定功率/kW額定容量/kWh安裝成本/(萬元·kW-1)使用年限/年運行維護成本/(元·kWh-1)最大剩余容量/%最小剩余容量/%充電效率放電效率自放電率201000.066 7100.083 2100100.90.90.001

3.3 優化結果

利用Matlab求解優化模型，在滿足各分布式電源的約束前提下，以提高微電網的經濟性與可靠性為前提，得出各分布式電源在各時刻的出力。微電網的負荷往往具有隨機性，每日的負荷曲線差異較大，需驗證此優化調度模型能否滿足各類型的負荷需求。根據圖2選取負載曲線L1至L3進行優化驗證，各負載情況下的系統運行優化結果見圖3至圖5。

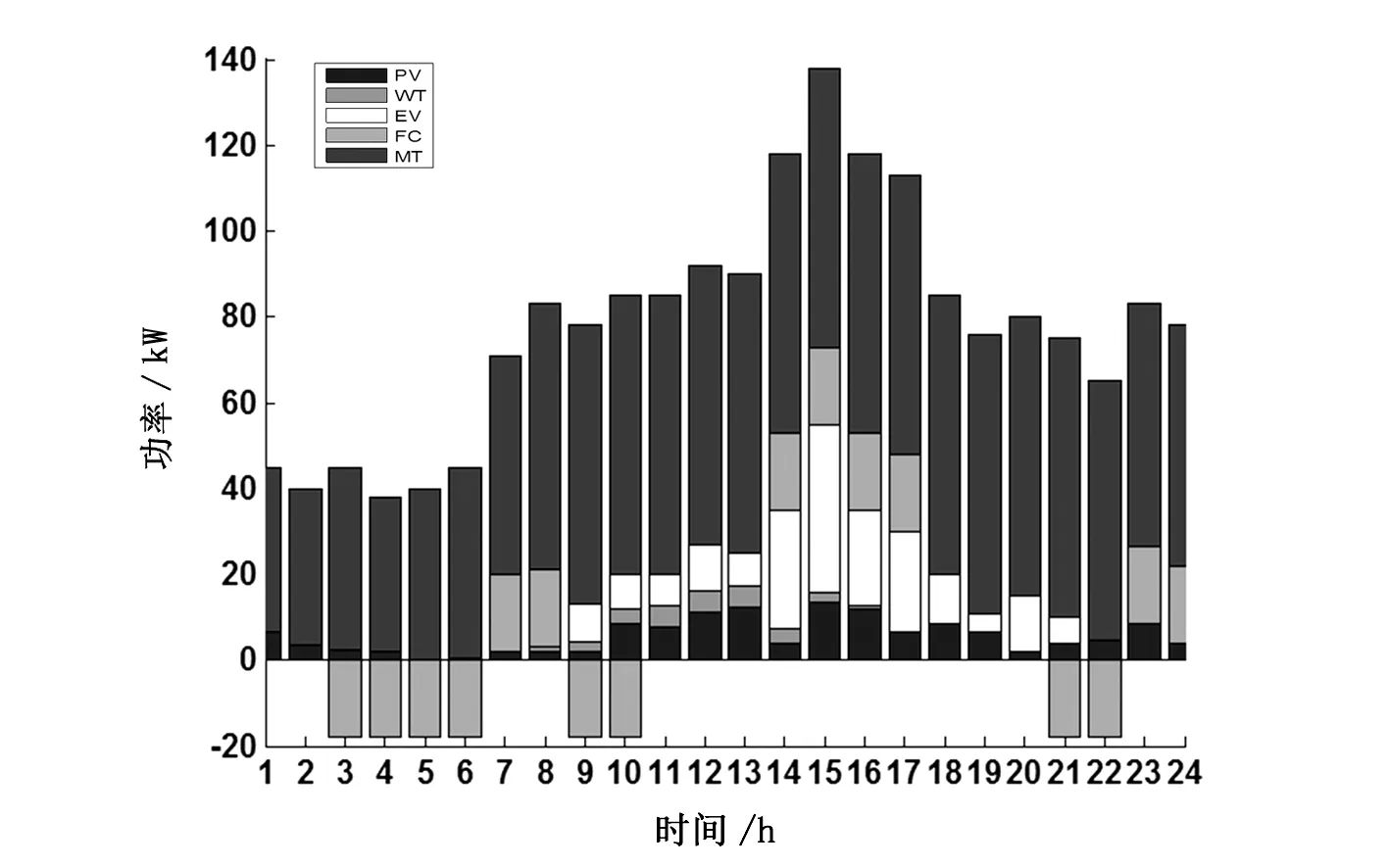
圖3 情況1時的優化結果

圖3為系統在負荷曲線1 下的運行優化結果。根據圖2負荷特性可知，在0:00—06:00期間為負荷的低谷時期，因此蓄電池切換至充電模型，其電能由風電及微型燃氣輪機發電提供；14:00—17:00為負荷高峰期，且系統的負荷需求高達140 kW，此時微型燃氣輪機已滿發，需利用蓄電池放電，滿足系統的負荷需求，保障系統的穩定運行。

圖4 情況2時的優化結果

圖4為系統在負荷曲線2下的運行優化結果。負荷曲線2的負荷高峰期為19:00—22:00。如圖4所示，此高峰時段微型燃氣輪機已滿發，需要蓄電池配合放電才可以滿足系統負荷需求。由于該負荷條件下負荷高峰期時間出現較晚，此時蓄電池雖然已經過了兩次充放電的轉換，但依舊是滿電量狀態，因此在保證系統可靠性的同時保障了運行的經濟性。

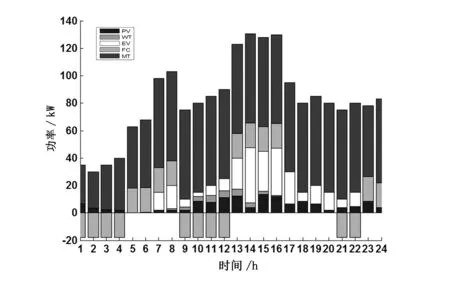
圖5 情況3時的優化結果

圖5為系統在負荷曲線3下的運行優化結果。負荷曲線3的負荷低谷期為0:00—04:00，因此蓄電池在較早時開始充電，隨后根據負載變化不斷切換放電、充電，但依舊保證了在負荷高峰期時達到滿電量狀態，從而滿足負荷高峰期的系統調度需求。

4 結 語

建立了在保障微電網運行可靠性的前提下，以提高微電網的經濟性與環保性為目標的優化調度模型，加大了蓄電池在微電網系統中的比重。所建立的模型包含風、光、微型燃氣輪機、燃料電池、蓄電池，考慮能量供需平衡、爬坡速率約束及蓄電池充放電容量等約束條件。在3個負荷場景下，檢驗負荷的不確定性對微電網調度優化的影響，實驗證明，所建立的微電網模型可有效工作于負荷不確定的模式。

[1] 楊毅,雷霞,葉濤,等. 考慮安全性與可靠性的微電網電能優化調度[J]. 中國電機工程學報,2014,34(19):3080-3088.

[2] 趙磊,曾芬鈺,王霜,等. 基于經濟性與環保性的微電網多目標優化調度研究[J]. 高壓電器,2015,51(6):127-132.

[3] 胡漢梅,李靜雅,黃景光. 基于改進雞群算法的微電網優化運行研究[J]. 高壓電器,2017,53(2):19-25.

[4] 邱曉燕,趙勁帥,史光耀,等. 基于HSMOPSO算法的微電網經濟與環保協同優化方法[J]. 高電壓技術,2017,43(4):1223-1230.

[5] 趙波,薛美東,陳榮柱,等. 高可再生能源滲透率下考慮預測誤差的微電網經濟調度模型[J]. 電力系統自動化,2014,38(7):1-8.

[6] 牛銘,黃偉,郭佳歡,等. 微網并網時的經濟運行研究[J]. 電網技術,2010,34(11):38-42.

[7] 吳雄,王秀麗,王建學,等. 微網經濟調度問題的混合整數規劃方法[J]. 中國電機工程學報,2013,33(28):1-9.

[8] Gouveia C, Moreira J, Moreira C L, et al. Coordinating Storage and Demand Response for Microgrid Emergency Operation[J]. IEEE Transactions on Smart Grid, 2013, 4(4):1898-1908.

[9] 洪博文,郭力,王成山,等. 微電網多目標動態優化調度模型與方法[J]. 電力自動化設備,2013,33(3):100-107.

[10] 劉嬌嬌,王致杰,袁建華,等. 基于PSO算法的風光儲微電網優化調度研究[J]. 華東電力,2014,42(8):1534-1539.