中心吸氣式超聲速飛行器動載荷識別

王驍峰，段 毅，袁銳之

(空間物理重點試驗室， 北京 100076)

飛行器在飛行過程中，常會遇到各種外界動態干擾力，稱速變力。當這些速變力的變化頻率接近飛行器結構或結構單元體的自身振動固有頻率時，將會激起飛行器的橫向彎曲振動和結構單元體的振動，產生動載荷[1-2]。吸氣時超聲速飛行器具有強耦合性、不確定性等特點[3]。一般吸氣式飛行器多為細長外形，其固有頻率和結構剛度較低，易產生顯著的彈性變形[3]，且其設計具有內外流一體化特征，既要使飛行器具有較高的升阻比，又要保證進氣道的進氣通暢[4]。飛行器受到非常復雜的氣流擾動，會出現低頻整體彈性響應的動載荷[5]。

中心吸氣式超聲速飛行器一般采用兩級串聯動力組合方式，一級為助推火箭發動機，二級為沖壓發動機(主發動機)。在該串聯動力組合方式中，沖壓發動機噴管出口處被助推發動機連接機構部分或全部堵住，內通道前端往往設計成開口狀態，內通道和燃燒室形成了前端開口、后端封堵或部分封堵的空腔，高速氣流從內通道前端流入空腔后，內通道內流場發生周期性低頻壓力振蕩，如圖1所示，即產生亥姆赫茲不穩定現象[6]。在這種低頻壓力振蕩的影響下，內通道前端會產生周期性溢流，并和外流場相互干擾，產生飛行器頭部區域的周期性法向干擾力，引起飛行器低頻振動，產生使飛行器的橫向彎曲振動的動載荷。

載荷識別屬于振動問題的第二類反問題[7-8]，是通過測量結構動態響應和系統特征求結構激勵的方法。一般結構動力學問題由響應分析、系統辨識、載荷(外力激勵)辨識組成；根據某種響應參數求另一種響應參數，可以稱其為響應識別[9]。

載荷識別最早出現于航空工業，之后逐漸擴展到其他領域[8]。目前，載荷識別技術主要有頻域和時域兩類方法[7-8]。頻域識別法如Hillary[10]的懸臂梁問題，李東升、郭杏林[8]的逆虛擬激勵法和奇異值分解法結合的方法，許斌等[11]進行了多自由度結構非線性恢復力時域識別，張青霞等[12]進行了結構損傷的載荷識別，王洪波等[5]利用工作模態辨識的方法對飛行器動載荷進行識別。時域研究法如文詳榮等[7]的精細逐步積分法，高偉，于開平等[13]的基于變尺度積分滑動平均的載荷識別方法，王萬金等[14]的基于一階切比雪夫廣義正交多項式的載荷識別等，以上基于頻域或時域的方法和研究都是關于外載荷辨識方面的研究，關于內力載荷辨識的研究成果相對較少。尹云玉[9,15]根據飛行遙測數據，基于小波分析、最小二乘擬合及模態疊加法對飛行器內力載荷進行了識別并和載荷實測結果進行對比，識別效果較好。本文根據遙測數據對飛行器內力載荷進行識別，通過復現加速度進行驗證，屬于一種間接的響應識別。

1 超靜定方程組的最小二乘法和動力學響應的模態疊加法

1.1 最小二乘法

對于超靜定方程組：

Xβ=y

(1)

其中：

如果矩陣XTX非奇異則β有唯一解

(2)

1.2 模態疊加法

飛行器的結構動力學方程可寫成：

(3)

令

X=φq

(4)

將(4)代入(3)并左乘φT，最終可得解耦的方程：

(5)

式(3)～式(5)中:M為質量矩陣;C為阻尼矩陣;K為剛度矩陣;F為外力函數列陣;X為位移列陣;φ為模態矩陣;q為廣義坐標(廣義位移)列陣;qi為第i階模態的廣義坐標;Mi為第i階模態的廣義質量;ωi為第i階模態的圓頻率;ξi為第i階模態的阻尼比;Fi第i階模態的廣義力。

求解式(5)，可得廣義坐標qi，通過式(4)將模態空間的物理量轉換成物理空間的物理量；飛行器的截面彎矩和截面剪力可由前n階模態彎矩與模態剪力和廣義位移疊加而成：

(6)

式(6)中，W、Q為飛行器某截面的彎矩及剪力，Wj、Qj為飛行器第j階模態的模態彎矩及模態剪力，qj為第j階廣義坐標。

在本文的載荷識別中，廣義坐標qj并非直接由動力學方程式(5)直接求解而來，而是對飛行器低頻振動傳感器的測量數據進行辨識，求得廣義坐標，從而利用模態疊加法實現載荷識別。

2 廣義坐標的辨識

對某中心吸氣式超聲速飛行器飛行試驗的低頻振動數據進行廣義坐標辨識，四個低頻振動傳感器如圖2所示1#～4#位置。

根據式(1)，建立超靜定方程組：

(7)

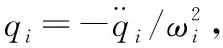
由圖3可見，1階廣義坐標幅值最大，是影響動載荷大小的主要因素，3階廣義坐標最小，其對動載荷的影響可忽略不計。以下動載荷識別僅考慮1階和2階廣義坐標的影響。

3 飛行器動載荷識別

由模態計算或模態試驗可以得到模態彎矩和模態剪力，則根據式(6)，由模態疊加法根據前2階模態可出求飛行器任意截面的動彎矩和動剪力。圖4(見封三)及圖5(見封三)給出了飛行器從起飛到助推分離時間段的10個截面(圖2所示1～10個截面位置)的動彎矩和動剪力的識別結果。由圖4及圖5可以看出，在6.8～10.3 s的時間段動載荷最大，其他外力干擾引起的動載荷相對較小，說明內通道低頻壓力振蕩是引起飛行器動載荷的唯一因素。

4 廣義坐標辨識的正確性驗證

動載荷識別時，如果有動載荷飛行試驗實際測量值，可將識別結果和實際測量值對比[8]。由于飛行試驗時飛行器并未測量飛行器飛行狀態的實際動載荷，因此無法將識別的動載荷和實際測量值直接對比。但是，可以根據式(7)，將模態矩陣左乘辨識得到的廣義加速度，復現物理空間的加速度，并和遙測低頻振動加速度對比，用來驗證廣義坐標辨識和動載荷識別的正確性。對比結果如圖6～圖9(見封三)所示。

圖中可以看出，1#、3#、4#的復現結果和遙測結果非常吻合，2#的復現結果和遙測結果的吻合度較差。究其原因，2#位于一階振型的節點處，此處的振型數值較小，測量的相對誤差較大；而此處振型微小的絕對誤差會引起較大的相對誤差，出現病態矩陣[16]，導致復現結果吻合度較差。為避免這種情況出現，最好的辦法就是選取離振型節點較遠的傳感器數據進行辨識。本文1#、3#、4#的復現結果和遙測結果非常吻合。根據式(7)，采用三個傳感器即可辨識前三階模態的廣義位移。從1#、3#、4#傳感器復現的結果看，廣義位移的辨識方法是可信的，說明飛行器的動載荷的識別結果可靠。

5 結論

1) 本文敘述的動載荷識別方法，不但適用于中心吸氣式超聲速飛行器的飛行動載荷識別，也適用于其他飛行器的飛行動載荷識別。當飛行器受外界動態干擾的外力函數不明確時，可以運用該法對飛行器動載荷加以識別，達到指導載荷設計的目的。

2) 通過式(7)可對廣義坐標辨識的結果的正確性進行驗證：根據辨識得到的廣義加速度反算出物理空間的加速度并和遙測低頻振動加速度進行對比，不失為一種有效驗證方法。

3) 飛行器內通道的低頻壓力振蕩是引起的飛行器彈體動載荷的主要原因，由內通道低頻振蕩壓力引起的彈體動載荷是飛行器動載荷的最主要成分，這在載荷設計時必須予以充分考慮。

4) 對于飛行器的結構動特性而言，由于飛行器的一階模態頻率一般較低，其一階模態頻率往往和內通道低頻壓力振蕩頻率比較接近，容易激起較大彎曲振動的動載荷響應，這在載荷設計和結構設計時應予以足夠重視。

[1] 黃壽康.流體動力·彈道·載荷·環境[M].北京:宇航出版社,1991.

[2] 龍樂豪.總體設計(上)[M].北京：宇航出版社,1989.

[3] 王勇,張艷,白辰,等.吸氣式高超聲速飛行器制導與控制方法綜述[J].兵器裝備工程學報,2017，38(4)：72-76.

[4] 焦子涵,王雪英,范宇,等.類乘波前體進氣道一體化設計與仿真研究[J].兵器裝備工程學報,2016， 37(9)：152-156.

[5] 王洪波,趙長見,廖選平,等.基于飛行工作模態分析的飛行器動載荷識別研究[J].動力學與控制學報，2017,15(4):178-183.

[6] 唐碩,祝強軍.吸氣式高超聲速飛行器動力學建模研究進展[J].力學進展,2011,41(2):187-200.

[7] 文祥榮,智浩,孫守光.結構動態載荷識別的精細逐步積分法[J].工程力學,2001,18(4):117-122.

[8] 李東升,郭杏林.逆虛擬激勵法隨機載荷識別試驗研究[J].工程力學,2004,21(2):134-139.

[9] 尹云玉.固體火箭自由運行狀態截面彎矩識別方法[J].宇航學報,2010,31(7):1706-1710.

[10] HILLARY B,EWINS D J.The use of strain gages in force determination and frequency response measurements[C]//Proceedings of 2nd International Modal AnalysisConference.New York:Society for Experimental Mechanics,1984:627-634.

[11] 許斌,辛璐璐,賀佳.基于切比雪夫多項式模型的多自由度結構非線性恢復力時域識別[J].工程力學,2014,31(11):99-109.

[12] 張青霞,段忠東,LUKASZ JANKOWSKI.結構損傷與載荷共同識別的研究[J].工程力學,2012,9(12):316-321.

[13] 高偉,于開平,蓋曉男.一種基于變尺度積分滑動平均的載荷識別方法[J].工程力學,2016,33(7):39-47.

[14] 王萬金,玄志武,張志國.切比雪夫多項式在動態載荷識別中的應用[J].強度與環境,2013,40(6):1-7.

[15] 尹云玉.固體火箭橫向響應載荷識別方法[J].宇航學報,2009,30(6):2135-2139.

[16] 李慶陽,王能超,易大義.數值分析[M].北京：清華大學出版社，2001.