考慮輪輻剛度和齒廓修形的漸開線直齒輪動載荷研究

李春明， 王成， 杜明剛， 趙志剛

(1.中國北方車輛研究所 車輛傳動重點實驗室， 北京 100072； 2.陸軍裝備部 項目管理辦公室， 北京 100072)

0 引言

隨著車輛傳動系統向高速、重載的方向發展，在內、外激勵共同作用下傳動系統產生較強振動，降低了安全性、可靠性和工作質量，嚴重時甚至造成齒輪、傳動軸和軸承等零件的破壞。以往針對高速重載車輛傳動系統動態性能研究主要以線性扭轉振動為主[1-2]，實際上傳動系統的振動形式包括扭轉振動、彎曲振動等，并且這些振動大多是以相互耦合的形式存在的[3-4]。間隙、時變剛度和加工誤差等成為齒輪傳動系統動力學研究中重要的非線性因素[5]。

修形是降低齒輪傳動系統振動和提高可靠性的關鍵技術。其中，齒廓修形可有效地緩和嚙合齒數變化時引起的嚙合剛度急劇變化，降低齒輪傳動系統的振動[6]。文獻[7-8]分別基于有限元模型和解析模型提出了定量計算修形齒輪嚙合剛度的計算方法。Lin等[9]基于2自由度非線性動力學模型，研究了直線和拋物線修形對動載荷影響。文獻[10-11]分別針對兩級定軸齒輪傳動系統和行星齒輪系統，采用不同動力學模型對比分析了齒廓修形對動態特性影響。王成等[12]建立了考慮齒輪運動狀態和嚙合狀態的嚙合剛度模型，研究了波動轉矩作用下齒廓修形對動態特性影響。Marcello等[13]采用優化設計方法，對比研究了靜態傳遞誤差和動態傳遞誤差最小時對應的齒廓修形參數。文獻[14-15]將有限元法計算的嚙合剛度代入動力學分析模型中，研究了含有不同修形量和修形長度齒輪的動態行為。楊玉良等[16]建立了具有12自由度的平行軸系斜齒輪轉子系統動力學模型，研究了不同修形量對斜齒輪傳動振動響應影響規律。王成等[17]和Liu等[18]建立了單級齒輪傳動系統10自由度的橫- 扭- 擺耦合非線性動力學模型，研究了齒廓修形對動載荷影響，并以減小齒輪傳動系統的動載系數為目標開展了齒廓修形優化設計。綜上所述，為提升高速重載車輛傳動系統的功率密度，漸開線直齒輪普遍采用薄壁輪緣結構，而綜合考慮薄壁輪緣結構和齒廓修形對嚙合剛度影響，并開展齒輪動載荷研究的文獻尚不多見。

本文考慮輪輻剛度、齒廓修形和齒輪實際運行狀態，采用解析法計算嚙合剛度，建立了齒輪嚙合剛度模型。考慮幾何偏心、陀螺力矩和齒向偏載力矩，建立了10自由度橫- 扭- 擺耦合非線性動力學模型，并將嚙合剛度模型和非線性動力學模型進行耦合計算。從定性和定量角度，對比分析了兩種輪體結構齒輪動載荷隨轉速、扭矩、修形量和修形長度的變化趨勢，所得結論可為齒輪減振和輕量化設計提供理論參考依據。

1 考慮輪輻剛度和齒廓修形的嚙合剛度模型

1.1 齒廓修形齒輪嚙合剛度模型

齒廓修形包括齒頂修形和齒根修形[6]，本文僅考慮齒頂修形(見圖1)并將修形量表示為嚙合線長度的函數。齒頂修形有多種類型，其中線性修形最常用，如(1)式所示：

(1)

式中：C為任意修形位置的修形量；s為任意修形位置的嚙合線長度，s∈[sb,se]，sb和se分別為修形起始點和修形終止點對應的嚙合線長度；Cmax為齒頂位置的最大修形量。

圖1中，L為修形長度，rb為基圓半徑。

嚙合剛度隨著嚙合位置的變化而不斷變化，表示為嚙合點壓力角的函數，結合單、雙齒嚙合和修形區動態邊界條件，齒頂修形齒輪的嚙合剛度計算分為5種情況[17-18]：1)嚙合點在單齒嚙合區內；2)嚙合點在雙齒嚙合區內；3)嚙合點在齒輪1修形區內；4)嚙合點在齒輪2修形區內；5)嚙合點同時在兩個齒輪修形區內，其中，修形區的嚙合剛度采用文獻[7]方法計算。5種情況的嚙合剛度分別為

(2)

(3)

(4)

(5)

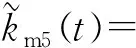
(6)

式中：αm(t)為嚙合點壓力角，是轉速和中心距的時變函數[17]；ks(αm(t))為單對齒嚙合剛度；ks1(αm(t))和ks2(αm(t))分別為雙齒嚙合時不同齒對的嚙合剛度；Fm(t)為動態嚙合力；C1(t)和C2(t)分別為齒輪1和齒輪2的修形量；中間變量E1(t)、E2(t)和E3(t)分別為

E1(t)=δ1(t)-C1(t)，

(7)

E2(t)=δ2(t)-C2(t)，

(8)

E3(t)=C1(t)-C2(t)，

(9)

δ1(t)=Fm(t)/ks1(αm(t))，

(10)

δ2(t)=Fm(t)/ks2(αm(t))，

(11)

δ1(t)和δ2(t)為雙齒嚙合時不同齒對的變形量。

采用解析法計算單對齒嚙合剛度[6]：

(12)

式中：δBj(αm(t))為齒輪j輪齒本身的變形，采用Weber法并結合Cornell的判斷條件計算；δC為輪齒之間的接觸變形，采用赫茲接觸模型計算；δMj(αm(t))為齒輪j輪體附加變形，本文考慮薄壁輪緣結構，采用1.2節解析方法計算。

1.2 薄壁輪緣齒輪輪體附加變形

將輪體分成3個部分，如圖2所示。將每個部分看作內圈固定而外圈承受扭矩，則外圈相對于內圈將產生轉角形變量，將3個部分的形變量疊加，可得輪體的總形變量。圖2中：lr為輪緣處齒厚；lw為輻板處齒厚；lh為輪轂處齒厚；rh為第2部分圓孔中心與圓環中心的距離；dh為第2部分圓孔的直徑；di1為輪轂內直徑，do1為輪轂外直徑；di2為輪緣內直徑；do2為輪緣外直徑。

1) 對于第1部分，設輪體承受扭矩為M，則任意橫截面所受的扭矩為Mr=M/lr. 在截面半徑為ρ處取寬度為dρ的微小圓環，其圓周位移為

(13)

式中：G為剪切模量。則圓環總的圓周位移為

(14)

2) 對于第2部分，無圓孔處的計算方法與第1部分相同。對圓孔部分，半徑為ρ的微小圓環穿過其中的1個圓孔.ρ與rh之間的夾角為

(15)

設有n個圓孔，則圓孔外的圓環有效長度為

(16)

有效部分的圓環上所受剪應力τ=M/(ρlwL)，剪應變為

(18)

則寬度為dρ微小圓環的圓周位移為

(18)

穿過圓孔部分圓環的總圓周位移為

(19)

將無圓孔和有圓孔部分的圓周位移疊加，可得到第2部分的總圓周位移s2為

(20)

3)對于第3部分，將(14)式中的lr變為lh，且積分區間變為[di1/2,do1/2]，可得總圓周位移s3為

(21)

將3個部分相加可得到輪體總的圓周位移，再除以輪體半徑，得到輪體轉角為

θt=2(s1+s2+s3)/d1，

(22)

式中：s1、s2和s3分別為3個部分的圓周位移；d1為輪體直徑。則薄壁輪緣齒輪的輪體附加變形為

δMi=θtRi，

(23)

式中：Ri為齒輪i的基圓半徑。

1.3 嚙合剛度有限元結果對比

采用有限元法計算單對齒嚙合剛度并與本文解析法進行對比。齒輪副結構參數見表1，其中，方案1的輪體為實體，方案2的輪體為薄壁輪緣結構。

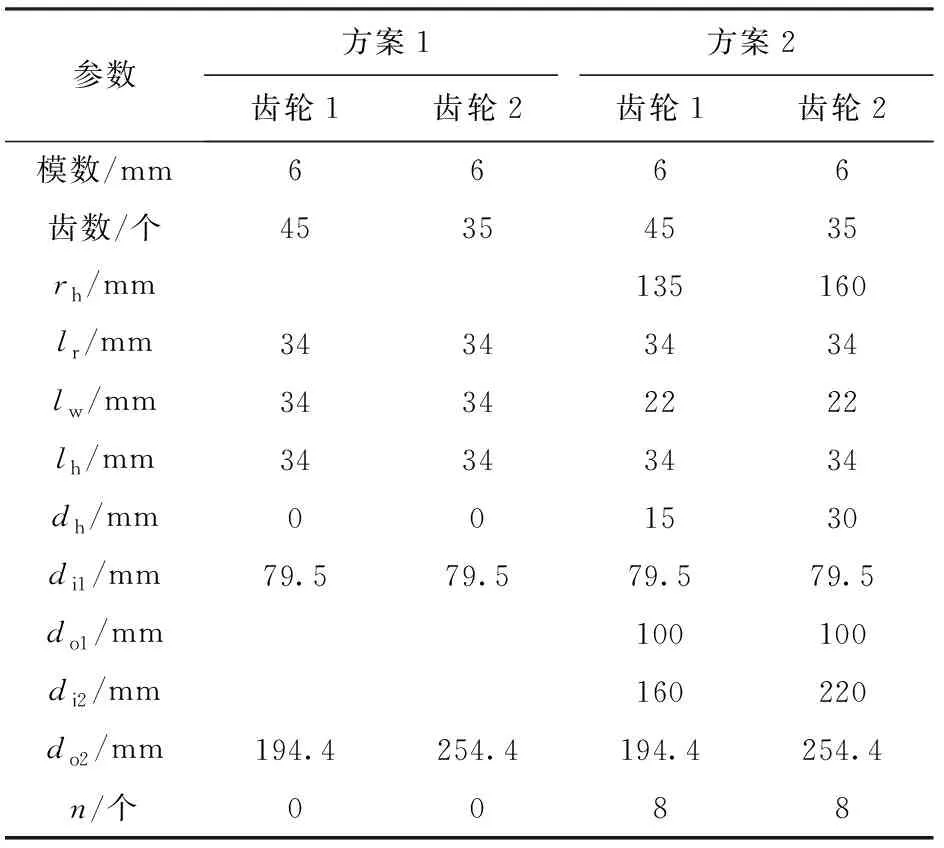
表1 齒輪副結構參數

不考慮接觸變形，在齒輪內徑施加固定約束，在兩齒輪對應的嚙合位置分別施加沿嚙合線方向齒寬上均勻分布的載荷F，可得沿嚙合線方向的變形量分別為δ1和δ2，則單對齒嚙合剛度[19]為

(24)

式中：k1=F/δ1；k2=F/δ2.

薄壁輪緣齒輪1的三維有限元模型如圖3所示。兩種方案有限元計算結果和解析計算結果如圖4所示。由表4可以看出，兩種方法的計算結果吻合較好，最大誤差小于6%，驗證了薄壁輪緣齒輪嚙合剛度計算模型的正確性。另外，方案2薄壁輪緣齒輪的嚙合剛度較方案1實體齒輪的嚙合剛度明顯減小。

2 非線性動力學建模

針對圖5所示的齒輪傳動系統進行動力學建模，滾動軸承簡化為彈性支撐，齒輪中心等效為傳動軸和軸承的串聯支撐；齒輪副通過沿著嚙合面的作用力耦合在一起，嚙合面始終與兩齒輪的基圓相切。

齒輪傳動三維動力學模型如圖6所示，圖6中有兩種坐標系：第1種為各齒輪的局部坐標系oixiyizi，oi為傳動軸理論中心位置；第2種為固定坐標系OXYZ，它與齒輪1的局部坐標系重合。A1A2B2B1為齒輪副間的嚙合面。每個齒輪包含2個橫向平移自由度xi和yi、1個扭轉自由度θzi以及2個擺動自由度θxi和θyi. 圖6中，Ci為質心，ei為偏心距，ψi為質心位置的初始轉角。下標i=1代表齒輪1，i=2代表齒輪2.

考慮幾何偏心、陀螺力矩和齒向偏載力矩，由拉格朗日方程可得單級齒輪傳動系統的橫- 扭- 擺耦合非線性動力學方程[17-18, 20-21]為

(25)

(26)

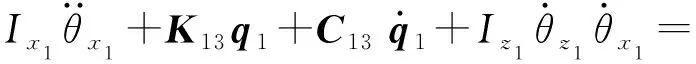
(27)

(28)

(29)

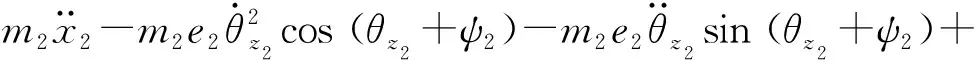
(30)

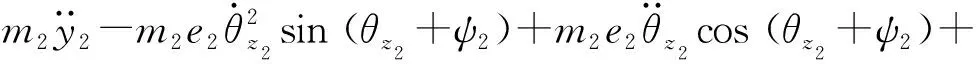
(31)

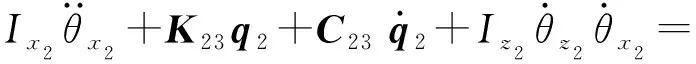
(32)

(33)

(34)

式中：kh為齒向偏載系數；α(t)和γ(t)分別為動態嚙合角和位置角；mi為質量；Ixi、Iyi和Izi分別為轉動慣量；Ti為外部激勵；qi=[xi,yi,θxi,θyi,θzi]T；Kij和Cij分別為齒輪i中心支撐剛度矩陣和阻尼矩陣的第j行；下標i=1代表齒輪1，i=2代表齒輪2；下標j=1,2,3,4,5.

齒輪副通過沿嚙合線方向上的嚙合剛度、嚙合阻尼和齒側間隙耦合在一起，動態嚙合力為

(35)

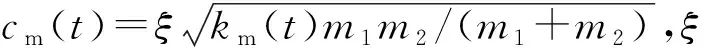
(36)

(37)

Δ(t)=(x1-x2)sin (α(t)+γ(t))-
(y1-y2)cos (α(t)+γ(t))+R1θz1-R2θz2+e(t)，

(38)

e(t)為齒廓修形引起的齒形偏差。

3 動載荷參數影響規律研究

針對表1所示齒輪副進行動載荷參數影響規律研究，動力學參數見表2，其中，單齒嚙合最高點對應的修形長度為Lh=5.3 mm，當修形長度小于Lh為短修形，超過Lh為長修形。為描述齒輪動載荷隨參數的變化規律，定義動載系數為

(39)

式中：Fmax為仿真時間內動態嚙合力最大值；Fs為理論嚙合力；Fm(t)為動態嚙合力。

表2 齒輪動力學參數

3.1 兩種輪體結構下轉速扭矩對動載荷影響

不考慮齒廓修形，輸入額定扭矩2 850 N·m，轉速變化范圍為[800 r/min, 2 300 r/min]，動載系數隨轉速的變化趨勢如圖7所示。由圖7可見，隨著轉速增加，兩種方案的動載系數均呈駝峰狀變化，多數轉速下薄壁輪緣齒輪的動載系數較大，最大增幅為6%. 方案1在轉速為1 650 r/min時的動載系數最大為1.784，較轉速為1 300 r/min時的最小動載系數1.458增加了22.3%；方案2在轉速為1 650 r/min時的動載系數最大為1.835，較轉速為1 350 r/min時的最小動載系數1.484增加了23.6%.

輸入轉速2 050 r/min，此時齒輪嚙合剛度和動態嚙合力分別如圖8和圖9所示。由圖8和圖9可見，兩種方案在單、雙齒嚙合交替時均存在明顯的剛度突變現象，且薄壁輪緣齒輪的單、雙齒嚙合剛度明顯降低。薄壁輪緣齒輪的嚙入沖擊載荷增加，造成動載系數較大。由圖10可知，兩種方案的動態嚙合力均以第2階、第5階和第6階嚙頻對應幅值為主，其中，薄壁輪緣齒輪的動態嚙合力2倍嚙頻和6倍嚙頻幅值明顯增加。

不考慮齒廓修形，輸入額定轉速2 300 r/min，扭矩變化范圍為[500 N·m,3 000 N·m]，動載系數隨扭矩的變化趨勢如圖11所示。由圖11可見：隨著扭矩增加，動載系數總體均呈拋物線減小的趨勢，但薄壁輪緣齒輪的動載系數在個別轉速下存在局部峰值；兩種方案的動載系數隨轉矩變化均不敏感，其中，方案1在扭矩為1 850 N·m時的動載系數最小為1.660，在扭矩為500 N·m時的動載系數最大為1.698；方案2在扭矩為1 850 N·m時的動載系數最小為1.649，在扭矩為700 N·m時的動載系數最大為1.690.

輸入扭矩為3 000 N·m，此時動態嚙合力時域曲線如圖12所示。由圖12可以看出，兩種方案的嚙入沖擊載荷基本相同，動載系數差別較小。由圖13可知，兩種方案的動態嚙合力均以2階、4階和5階嚙頻對應幅值為主，其中，薄壁輪緣齒輪的動態嚙合力2倍嚙頻對應的幅值明顯減小。另外，薄壁輪緣齒輪5倍嚙頻幅值增加是出現局部峰值的主要原因。

3.2 兩種輪體結構下齒廓修形對動載荷影響

兩齒輪修形量和修形長度相同，其中，修形量取值范圍為[0 mm, 0.1 mm]，取值間隔為0.001 mm，修形長度為2 mm. 在額定轉速和扭矩工況下，動載系數隨修形量變化如圖14所示。由圖14可以看出，隨著修形量增加，動載荷系數均呈U形變化，即存在最優修形量使動載荷系數達到最小。當修形量超過最優值時，方案1的動載系數增加明顯，而方案2的動載系數變化趨勢緩慢。兩種方案對應的最優修形量均為0.019 mm，對應的動載系數分別為1.376和1.385，分別較無修形齒輪的動載系數1.663和1.649減小了17.2%和16.0%. 兩種方案對應的最優修形量均小于額定轉矩作用下單齒嚙合最高點的變形量。另外，存在臨界修形量，當超過該值時齒輪動載系數大于無修形齒輪。兩種方案對應的臨界修形量分別為0.053 mm和0.073 mm. 在修形量為0.095 mm情況下，兩種方案的動載系數差別最大，其中，方案1動載系數為2.365，較方案2的動載系數1.848增加了21.9%.

針對薄壁輪緣齒輪，進一步對比無修形和最優修形齒輪(修形量0.019 mm)的嚙合剛度和動態嚙合力時域曲線，分別如圖15和圖16所示。由圖15、圖16可以看出，齒廓修形有效地緩和了單、雙齒嚙合交替時嚙合剛度的突變現象，同時齒廓修形有效地降低了嚙入沖擊載荷，動載系數明顯降低。由圖17所示的動態嚙合力頻域曲線可知，無修形齒輪的動態嚙合力幅值以2倍嚙頻、4倍嚙頻和5倍嚙頻為主，而修形齒輪的動態嚙合力幅值以1倍嚙頻、2倍嚙頻和5倍嚙頻為主。其中，修形齒輪1倍嚙頻的幅值顯著增加，而2倍嚙頻、4倍嚙頻和5倍嚙頻的幅值明顯降低。

兩齒輪修形量和修形長度相同，其中，修形量為0.02 mm，修形長度的取值范圍為[1.0 mm,6.0 mm]，取值間隔為0.1 mm. 在額定轉速和扭矩工況下，動載系數隨修形長度的變化趨勢如圖18所示。由圖18可見，隨著修形長度增加，兩種輪體結構齒輪的動載荷系數變化趨勢基本一致。當修形長度小于5.1 mm時，動載系數近似呈U形變化；當修形長度超過5.1 mm時，動載系數急劇減小。在修形長度為4.8 mm情況下，方案1的動載系數2.780較方案2的動載系數2.456增加了12.3%. 在短修形情況下，方案1和方案2對應的最優修形長度分別為2.5 mm和3.0 mm，對應的動載系數分別為1.335和1.352. 在長修形情況下，短修形和長修形對應的最優修形長度均為5.4 mm，對應的動載系數分別為1.060和1.128. 上述分析說明長修形可更有效地減低齒輪動載荷。

針對薄壁輪緣齒輪，進一步對比短修形3.0 mm和長修形5.4 mm的嚙合剛度和動態嚙合力時域曲線，結果分別如圖19和圖20所示。由圖19和圖20可知，長修形和短修形均有效地緩和了單、雙齒嚙合交替時嚙合剛度的突變現象。由圖20可知，長修形的動態嚙合力波動小于短修形，動載荷明顯降低。結合圖19和圖20，在修形區內，由于短修形動態嚙合力的波動范圍大，導致嚙合剛度存在明顯波動。由圖21所示的動態嚙合力頻域曲線可知，短修形齒輪的動態嚙合力幅值以1倍嚙頻、2倍嚙頻和4倍嚙頻為主，而長修形齒輪的動態嚙合力幅值以2倍嚙頻、4倍嚙頻和5倍嚙頻為主。除5倍嚙頻外，長修形齒輪動態嚙合力對應的幅值明顯降低。

4 結論

本文考慮輪輻剛度、齒廓修形和齒輪實際運行狀態，采用解析法計算嚙合剛度，建立了齒輪嚙合剛度模型，并與10自由度橫- 扭- 擺耦合非線性動力學模型實現了耦合計算。所得主要結論如下：

1)隨著轉速增加，兩種輪體結構齒輪的動載荷均呈駝峰狀變化；多數轉速下薄壁輪緣齒輪的動載荷較大，動態嚙合力第2階和第6階嚙頻對應的幅值增加明顯。

2)隨著轉矩增加，兩種輪體結構齒輪的動載荷總體均呈拋物線減小，但薄壁輪緣齒輪在個別扭矩下存在局部峰值，動態嚙合力在第2階和第5階嚙頻對應的幅值差別明顯。

3)隨著修形量增加，兩種輪體結構齒輪的動載荷均呈U形變化，即存在最優修形量使動載荷達到最小，且最優修形量和最小動載系數基本相同；當修形量超過某臨界值時，修形齒輪的動載荷大于無修形齒輪，且薄壁輪緣齒輪的臨界修形量較大。

4)隨著修形長度增加，短修形下動載荷均近似呈U形變化，長修形下動載荷急劇減小，說明長修形可更有效地降低齒輪振動。

參考文獻(References)

[1] 劉輝, 蔡仲昌, 曹華夏, 等. 基于iSIGHT平臺的車輛動力傳動系統聯軸器剛度優化研究[J]. 兵工學報, 2012, 33(2):228-231.

LIU Hui, CAI Zhong-chang, CAO Hua-xia, et al. The optimization study on the stiffness of coupling in vehicle powertrain based on iSIGHT platform[J]. Acta Armamentarii, 2012, 33(2):228-231.(in Chinese)

[2] 項昌樂, 何韡, 劉輝, 等. 履帶車輛傳動系統換擋工況瞬態動力學分析[J]. 農業機械學報, 2016, 47(4):288-293.

XIANG Chang-le, HE Wei, LIU Hui, et al. Transient dynamic analysis of tracked vehicle transmission during gear shift process[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4):288-293.(in Chinese)

[3] 劉輝, 項昌樂, 孫恬恬. 車輛動力傳動系統彎扭耦合振動模型的建立及復模態分析[J]. 機械工程學報, 2010, 46(24):67-74.

LIU Hui, XIANG Chang-le, SUN Tian-tian. Construction of bending-torsional coupled vibration model and complex modal analysis of the vehicle powertrain[J]. Journal of Mechanical Engineering, 2010, 46(24):67-74.(in Chinese)

[4] Liu H, Wang C, Xiang C L. Dynamic characteristic optimization of vehicle transmission based on lateral-torsional coupled nonlinear dynamic model[C]∥Proceedings of the 6th International Conference on Modelling, Identification & Control. Melbourne, Australia:IEEE, 2014: 149-154.

[5] 劉輝, 蔡仲昌, 朱麗君, 等. 多擋條件下單級行星傳動非線性振動特性研究[J]. 兵工學報, 2012, 33(10):1153-1161.

LIU Hui, CAI Zhong-chang, ZHU Li-jun, et al. Study on nonli-near vibration behavior of simple single stage planetary gears in multiple work conditions[J]. Acta Armamentarii, 2012, 33(10):1153-1161. (in Chinese)

[6] 李潤方. 齒輪傳動的剛度分析和修形方法[M]. 重慶:重慶大學出版社, 1998.

LI Run-fang. Mesh stiffness analysis and modification method of gear transmission[M]. Chongqing: Chongqing University Press, 1998. (in Chinese)

[7] Chen Z G, Shao Y M. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory, 2013, 62: 63-74.

[8] 唐進元, 蔡衛星, 王志偉. 修形圓柱齒輪嚙合剛度計算公式[J]. 中南大學學報:自然科學版, 2017, 48(2):337-342.

TANG Jin-yuan, CAI Wei-xin, WANG Zhi-wei. Meshing stiffness formula of modification gear[J]. Journal of Central South University: Science and Technology, 2017, 48(2):337-342. (in Chinese)

[9] Lin H H, Oswald F B, Townsend D P. Dynamic loading of spur gears with linear or parabolic tooth profile modifications[J]. Mechanism and Machine Theory, 1994, 29:1113-1129.

[10] Liu G, Parker R G. Dynamic modeling and analysis of tooth profile modification for multimesh gear vibration[J]. Journal of Mechanical Design, 2008, 130(12): 121402-1-121402-12.

[11] Bahk C J, Parker R G. Analytical investigation of tooth profile modification effects on planetary gear dynamics[J]. Mechanism and Machine Theory, 2013, 70:298-319.

[12] 王成, 劉輝, 項昌樂. 波動扭矩下漸開線直齒輪傳動齒廓修形研究[J].振動與沖擊, 2014, 33(24):32-38, 53.

WANG Cheng, LIU Hui, XIANG Chang-le. Influences of profile modification on dynamic characteristics of involute spur gears under a fluctuating torque[J]. Journal of Vibration and Shock, 2014, 33(24):32-38, 53. (in Chinese)

[13] Marcello F, Farhad S, Gabrieie B, et al. Dynamic optimization of spur gears[J]. Mechanism and Machine Theory, 2011, 46: 544-557.

[14] 陳思雨, 唐進元, 王志偉, 等. 修形對齒輪系統動力學特性的影響規律[J]. 機械工程學報, 2014, 50(7):39-45.

CHEN Si-yu, TANG Jin-yuan, WANG Zhi-wei, et al. Effect of modification on dynamic characteristics of gear[J]. Journal of Mechanical Engineering, 2014, 50(7):39-45.(in Chinese)

[15] 馬輝, 逄旭, 宋溶澤, 等.考慮齒頂修緣的齒輪- 轉子系統振動響應分析[J]. 機械工程學報, 2014,50(7)：39-45.

MA Hui, PANG Xu, SONG Rong-ze, et al. Vibration response analysis of a geared rotor system considering the tip relief[J]. Journal of Mechanical Engineering, 2014, 50(7):39-45.(in Chinese)

[16] 楊玉良, 魏靜, 賴育彬, 等. 考慮齒頂修緣的斜齒輪傳動振動響應分析[J]. 重慶大學學報, 2017, 40(1):31-40.

YANG Yu-liang, WEI Jing, LAI Yu-bin, et al. Vibration response analysis of helical gear transmission considering the tip relief[J]. Journal of Chongqing University, 2017, 40(1):31-40.(in Chinese)

[17] 王成, 劉輝, 項昌樂. 基于齒輪傳動系統橫- 扭- 擺耦合非線性動力學模型的齒廓修形優化設計[J]. 振動與沖擊, 2016, 35(1): 142-148.

WANG Cheng, LIU Hui, XIANG Chang-le. Optimal profile modification for spur gear systems based on their lateral-torsional-rocking coupled nonlinear dynamic model[J]. Journal of Vibration and Shock, 2016, 35(1): 142-148.(in Chinese)

[18] Liu H, Zhang C, Xiang C L, et al. Tooth profile modification based on lateral-torsional-rocking coupled nonlinear dynamic model of gear system[J]. Mechanism and Machine Theory, 2016, 105: 606-619.

[19] Chaari F, Fakhfakh T, Haddar M. Analytical modelling of spur gear tooth crack and influence on gear mesh stiffness[J]. European Journal of Mechanics A/Solids, 2009, 28(3):461-468.

[20] 劉輝, 張晨, 王成. 兩級漸開線齒輪傳動系統橫- 擺- 扭耦合非線性動力學建模與試驗驗證[J]. 振動與沖擊, 2017, 36(15):124-132.

LIU Hui, ZHANG Chen, WANG Cheng. Nonlinear dynamic modeling and test validation for a two-stage involute gear system[J]. Journal of Vibration and Shock, 2017, 36(15): 124-132. (in Chinese)

[21] 王成. 漸開線直齒輪傳動系統非線性動力學研究[D].北京： 北京理工大學, 2015.

WANG Cheng.Nonlinear dynamic research of involute spur gear system [D]. Beijing: Beijing Institute of Technology, 2015. (in Chinese)