弧形閘門支臂結構的非線性振動及混沌現象
張 健,謝智雄
(河海大學機電工程學院,江蘇常州213022)
0 引 言
弧形閘門支臂結構的安全影響著整個弧形閘門的安全,根據國內外對弧形閘門事故的調查分析發現:弧形閘門產生破壞的主要原因就是閘門支臂結構的失穩破壞,并且有文獻指出,只要動水壓力的激振能量不是很大,閘門不容易出現整體框架結構的振動,但是支臂發生單獨振動的可能性卻是很大的,因而有必要對弧形閘門支臂結構的非線性振動做進一步的分析研究。
混沌來源于非線性,在非線性振動過程中有可能存在混沌現象,在線性系統中不會產生。混沌存在于某些確定性的系統中,而且不需要任何附加的隨機因素。混沌振動具有以下的一些特點:由確定性因素產生,具有有界性,具有非周期性,對初始條件具有極端敏感性。本文通過有界性和非周期性來判斷弧形閘門支臂結構振動是否存在混沌現象,并通過功率譜圖和Lyapunov指數進一步確認了支臂結構振動確實存在混沌現象。
1 閘門支臂結構動力微分方程的建立
根據文獻[1],在一定開度下,弧形閘門泄流產生的動力荷載可以轉化為周期性變化的動水荷載,在考慮到考慮非線性影響因素后,其動力屈曲方程的一般形式為

(1)
式中,A,B,C是與梁的動力屈曲模態有關的常數矩陣;I為單位陣;f為廣義坐標列陣;Φ(t)為周期函數;α、β為荷載參數。
方程(1)是一個齊次非線性微分方程,而混沌只會發生在非線性系統中,因而研究方程(1)是有可能發現混沌現象的。
1.1 支臂結構的計算簡圖
根據國內外一些實測結果,將支臂結構按照兩端鉸接壓桿計算得到的自振頻率值與實測頻率值很接近,因此可以將支臂結構按照簡支梁模型來分析。本文將支臂看成是兩端鉸接的壓桿,在軸向干擾力的作用下進行動力穩定性分析,支臂結構的計算模型如圖1所示。

圖1 支臂結構計算模型
1.2 支臂結構動力學微分方程的建立
對于圖1所示的支臂結構的計算模型,在荷載的作用下支臂將產生橫向彎曲,根據文獻[3]發現支臂阻尼對支臂振動主要不穩定區域的影響較小,可忽略阻尼對支臂振動的影響。
根據支臂結構的計算模型,由動力平衡條件,建立無阻尼動力微分方程為
(2)
式中,E為彈性模量;I為截面慣性矩;p0+ptcos(θt)為周期性變化動水荷載;A為支臂橫截面面積;α為支臂的傾角;m為支臂的質量;v為支臂的撓度。

(3)
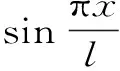
由式(3)可得
(4)
(5)
于是可得到無量綱形式的動力學微分方程

(6)

2 支臂結構振動的混沌現象
混沌是發生在確定性非線性系統中的貌似隨機的無規則運動,看似混亂無序,但是又頗有規律。由于系統的非線性,在滿足一定條件的振動系統中,即使是在受到規則的激勵后也會產生貌似無規則的永不重復的振動響應。混沌產生的主要原因就是系統對初始條件的十分敏感性,即使初始條件有微小的差別也有可能使得系統產生混沌現象。混沌運動的形態是十分復雜的,很難通過解析計算來描述,本文主要是通過計算機的數值仿真來實現對混沌現象的描述。
弧形閘門在發生振動時,支臂會產生動力不穩定區域,當非線性振動系統不穩定時,就有可能產生混沌現象,因此在研究混沌振動之前,要先解決系統振動穩定性問題。根據一些調查弧形閘門失事報告經過解析分析得出結論:在把支臂作為兩端鉸接的軸心壓桿,所施加的軸向干擾力為p(t),當干擾力的頻率θ等于支臂的橫向振動固有頻率Ω的2倍時,支臂將發生參數共振,喪失穩定。在本文中分析混沌振動時不妨取θ=2Ω,此時當施加的軸向干擾力的某些參數發生改變時,系統就有可能會發生混沌現象。

(7)

將以上數據整理后代入一階微分方程組(7),采用MATLAB程序利用四階龍格庫塔方法進行數值分析,繪制相圖、時程曲線圖、功率譜圖并計算Lyapunov指數,通過這些方法進行混沌的數值識別,當圖像滿足一定的條件時,即可判定該系統是否出現了混沌現象。混沌的相圖不是單獨的一條封閉的曲線,而是一個具有往復性并且局限在某一區域內的圖形;混沌運動是非周期性運動,功率譜譜線是類似于噪聲的連續譜線,但是利用功率譜圖還是很難區分真正的混沌運動和隨機運動的;而Lyapunov指數就能避免這個問題,只要當Lyapunov指數中有一個值是正值,此時就產生了混沌運動。
在實際工程中,脈動壓力幅值(即pt)是一個變量,因此在本文中以c為變量,通過選擇不同的值,利用程序繪制出相應的圖像。
取c=5,相圖和時程曲線如圖2、3所示。

圖2 相圖

圖3 時程曲線
顯然,相圖是一個環面,時程曲線圖是一個規則的周期圖像,因而這是一個周期運動。此時弧形閘門支臂沒有產生混沌現象。
取c=14,相圖和時程曲線如圖4、5所示。
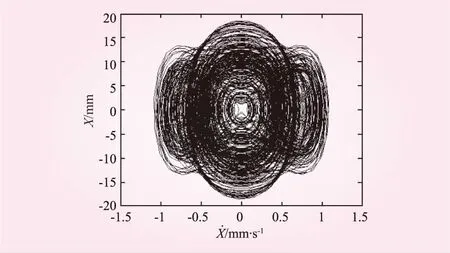
圖4 相圖

圖5 時程曲線
顯然,相圖是局限在一定區域內的不重復圖像,時程曲線圖是一個類似噪聲無規律譜線圖,因而在此時系統有可能出現了混沌現象。
取c=14.8,相圖、時程曲線圖如圖6、7所示。

圖6 相圖

圖7 時程曲線
顯然,相圖是局限在某一區域內永不重復的圖像,時程曲線圖是一種類似于噪聲的無規律譜線,因而可以判斷系統有可能存在混沌現象。
為驗證此時系統的確存在混沌現象,繪制功率譜圖和計算Lyapunov指數如圖8、9所示。

圖8 功率譜

圖9 Lyapunov指數
功率譜圖是一種類似于噪聲的無規律連續譜線,因而可判斷系統有可能存在混沌現象。
3 結 語
利用MATLAB程序數值模擬的方法,通過計算機繪制出的相圖、時程曲線圖、功率譜圖以及Lyapunov指數發現弧形閘門支臂結構在動水荷載的激勵下可能會產生混沌現象。在本文中,周期倍化是產生混沌的途徑,當c較小的時候,支臂結構在激勵下做周期振動,隨著c數值的增大,支臂非線性振動系統中產生了混沌。通過數值模擬的方法發現了混沌產生的途徑,對弧形閘門支臂結構的混沌振動有了更加直觀的認識。
[1] 朱召全, 卓家壽, 陶桂蘭. 弧形閘門的動力穩定性研究進展[J]. 水利水電科技進展, 1999, 19(5): 27- 29.
[2] 諶磊. 弧形鋼閘門空間框架的動力穩定性分析[D]. 西安: 西農林科技大學, 2006.
[3] 李火坤, 練繼建. 偏心荷載作用下弧形閘門支臂的動力穩定性研究[J]. 南昌大學學報, 2006, 28(1): 72- 77.
[4] 龍運佳. 混沌振動研究方法與實踐[M]. 北京: 清華大學出版社, 1996.
[5] 王聰玲, 龍運佳. 關于混沌振動的研究[J]. 中國農業大學學報, 1997, 2(6): 23- 27.
[6] 陜振沛, 寧寶權, 張轉周. 基于MATLAB的各類混沌系統的計算機仿真模擬研究[J]. 科技廣場, 2015, 6(1): 6- 11.
[7] 張靜. 混沌系統的計算機仿真[J]. 實驗室研究與探索, 2008, 27(8): 58- 59.
[8] 趙弘, 張登山. 混沌振動研究[J]. 鋼鐵研究, 2003, 134(5): 36- 40.
[9] 何四祥, 鄒祖軍. 混沌運動在一類非線性結構振動中的數值模擬研究[J]. 結構工程師, 2007, 23(1): 42- 44.
[10] 李娜, 趙鳳群, 王苗苗. 非保守簡支梁的非線性振動與混沌現象[J]. 陜西科技大學學報, 2011, 29(6): 56- 59.

