丹巴水電站彎道截流龍口局部水流水力特性分析

徐志惠，熊 毅

(1.武漢大學水利水電學院，湖北武漢430072； 2.中國市政工程中南設計研究總院有限公司，湖北武漢430010; 3.河南靈捷水利勘測設計研究有限公司，河南南陽473000)

1 研究背景

大渡河丹巴水電站采用枯水期圍堰擋水、隧洞導流，汛期導流隧洞和基坑聯合過流的導流方式。根據地形地質條件及樞紐布置情況，導流隧洞布置在左岸山體內，進口高程1 962.0 m，出口高程1 961.0 m，隧洞全長864 m，洞身斷面11.0 m×11.0 m(寬×高)，為城門洞形。戧堤上游設計邊坡1∶1.5，下游邊坡1∶1.5，頭部邊坡1∶1，戧堤頂高程1 973.5 m，設計流量取5年一遇旬平均流量517 m3/s，截流平面如圖1所示。

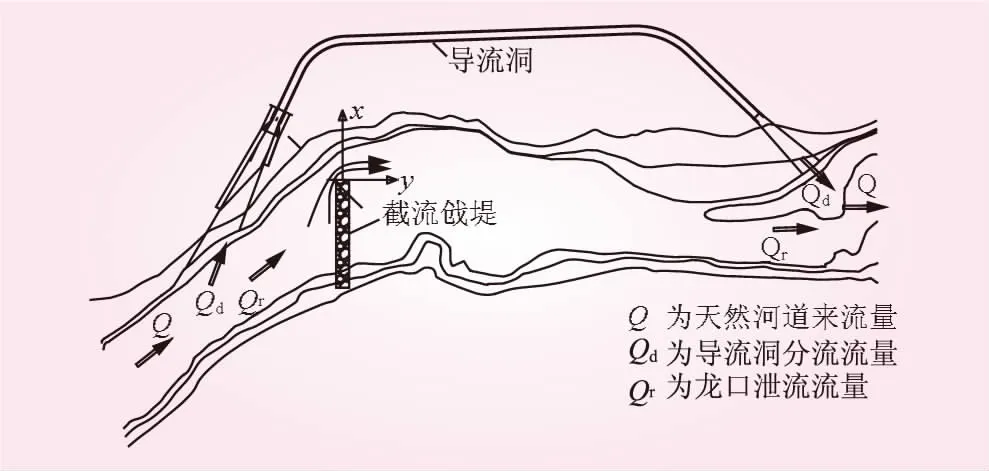
圖1 丹巴水電站截流平面布置示意

工程樞紐布置處河道存在約為35°的轉角，類似于局部彎曲河道，相對河寬B/r0可近似取為0.33，戧堤布置在彎道出口末端，采用立堵法從凸岸至凹岸單向進占，凹岸無預進占。受彎道影響，當進占至一定區間后，龍口進口前河寬明顯開始束窄，特別是戧堤堤頭上游坡腳處至彎曲岸坡束窄達到最大，如圖2所示。在束窄段的影響下，水流沿程水位于束窄段處即開始明顯下降，相應水流流速明顯增大。比較束窄段和龍口處的水深、流速、承擔的落差，束窄段對水流流態的改變與龍口起到相同的作用，可視為小龍口，即河道為雙龍口截流[1]。為探究小龍口的影響，本文以水力學理論為基礎，通過因素分析法建立計算模型，研究彎道影響下龍口上游堤頭處水流運動的變化，并通過物理模型試驗驗證計算模型及其分析方法的可靠性與適用性。

圖2 彎道截流龍口前束窄段示意

2 龍口局部水流特性分析

2.1龍口局部水流特性

彎道截流龍口如圖3所示，取龍口上游水流穩定處為斷面1-1，對1-1和c-c斷面、2-2和c-c斷面列能量方程：

(1)

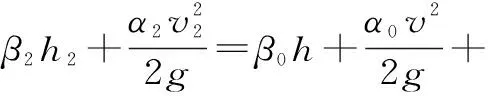
(2)

式中，h、H、h2分別為c-c、1-1、2-2斷面處的水深；β0、β1、β2分別為c-c、1-1、2-2斷面處的水流非靜力系數，緩變流時，β≈1，凸形水流β<1，凹形水流β>1[2]；龍口軸線α為動能修正系數[3]；fb為彎道阻力系數[4]；ξ為龍口進口處的局部水頭損失；v、v1、v2分別為c-c、1-1、2-2斷面處的水流速度。

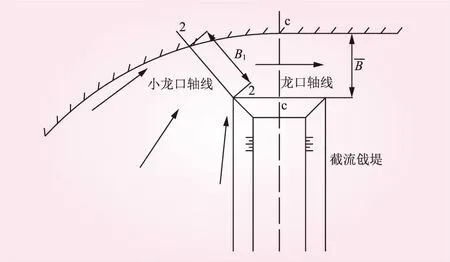
圖3 彎道截流龍口局部示意

由于束窄段水流相對龍口較為平穩，可取α1=α2=1，β1=β2=1，α0和fb的取值可參考文獻[5]的分析進行計算，如式(3)和式(4)所示；B、B1分別為雙龍口前最小束窄距離，如圖3所示，取束窄比為ψ=B1/B，顯然束窄比與彎道形態、戧堤位置和戧堤寬度b有關，對于固定的工程，ψ隨戧堤的進占變化而變化，即只與龍口進占束窄程度M有關，如圖4所示。

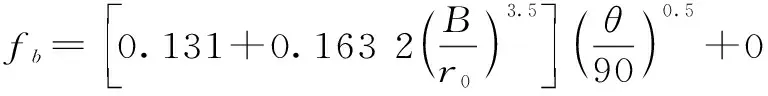
(3)

(4)

式中，r0為彎道中軸線曲率半徑；r1、r2分別為彎道

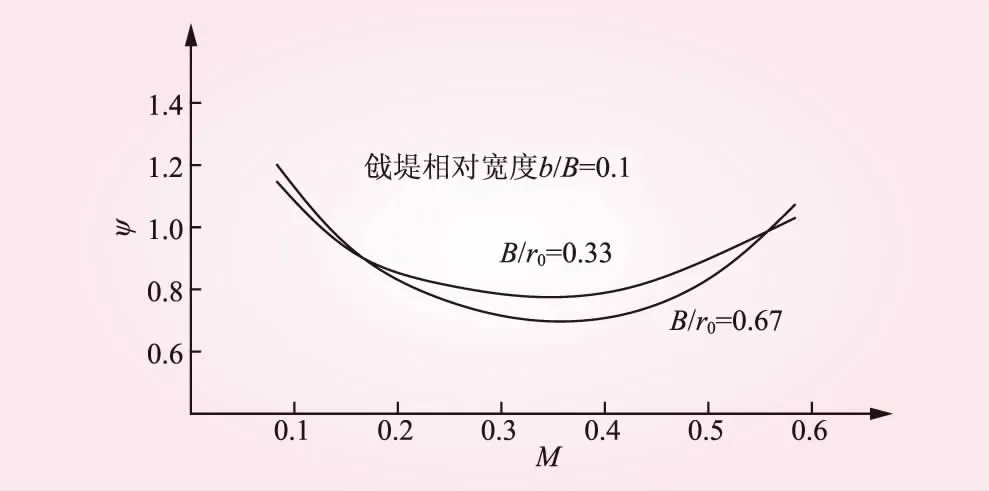
圖4 彎道截流束窄比 Ψ隨進占M變化的關系曲線

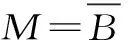
聯立式(1)、(2)，得

(5)

將上式進行無量綱化，得

(6)

根據彎道截流龍口水力特性的分析，α0和fb的取值主要與彎道形態系數(B/r0、θ)有關，同時結合龍口斷面軸線相對水深的計算式可知，龍口前束窄段水深主要受控于淹沒系數σ、龍口束窄系數、沿程損失系數η、水流不均勻系數、彎道形態系數、束窄比、龍口進口局部水頭損失等有關，即

h2/H=f(σ，M，η，β0，B/r0，θ，ψ，ξ)

(7)

2.2 彎道形態對龍口水深的影響

ψ與M具有對應關系，通過試驗發現淹沒系數和彎道形態對雙龍口效應影響較為顯著。因此本文采用單因素分析法，研究進占過程中σ和B/r0對雙龍口水深的影響。

2.2.1 淹沒流條件下

取η=0.5、θ=60°、β0=1.0，由于堤頭坡腳對水流的挑流作用非常明顯，可取ξ=0.2。考慮淹沒流的情況，取σ=0.1，得到小龍口相對水深h2/H～M關系曲線如圖5所示，雙龍口水深比h/h2～M的關系曲線如圖6所示。

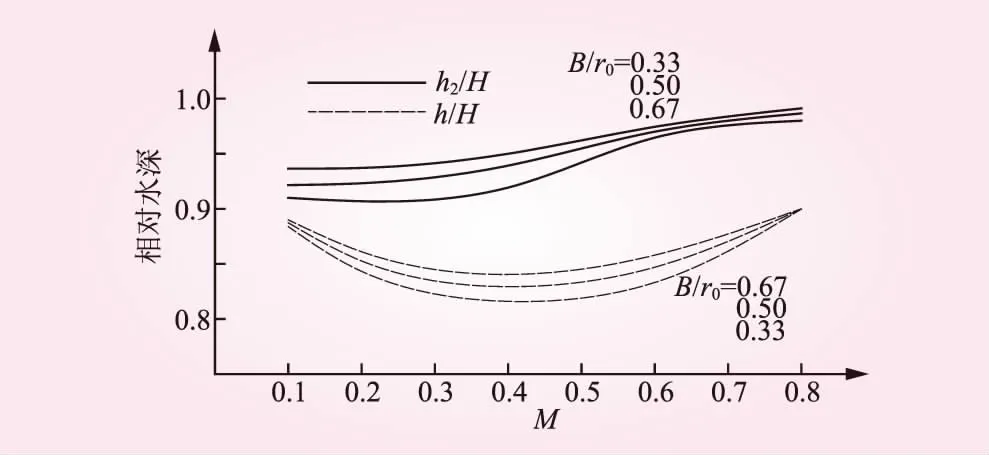
圖5 淹沒流條件下雙龍口相對水深隨進占的關系

圖6 淹沒流條件下雙龍口水深比隨進占的關系

由圖5、6可知，在進占初始階段，h2/H約為0.95～1.0，h/h2約為0.85～0.9，小龍口處水流水位變化不明顯，其承擔的水流落差較小，與正常河道的龍口前水面線規律類似，即可忽略雙龍口效應的影響；隨著進占的進行，當M在0.4～0.2時，h2/H約為0.95～0.9，h/h2約為0.9～0.95，小龍口處水流水位與龍口軸線水位較為接近，河道水面線在小龍口處即出現下降，小龍口開始承擔一部分落差，彎道截流開始呈現出雙龍口效應；當進占至截流最困難階段時，當M在0.2～0.1時，h2/H穩定為0.93～0.9，h/h2約為0.95～1.0，顯然，此時小龍口處水位與龍口軸線處水位非常接近，水流水面線在小龍口處顯著下降，在小龍口至龍口軸線范圍內以急流狀態平穩過渡，可認為小龍口與龍口共同承擔落差，彎道截流雙龍口效應明顯。對比不同彎道相對河寬下的雙龍口水深關系可知，B/r0值對小龍口水深有一定的影響，當B/r0在0.33～0.67時，h/h2在0.01～0.03內變化；彎道相對河寬越大，雙龍口效應越明顯，這是由于彎道相對河寬是體現彎曲河道特性的重要參數，B/r0越大，彎道特性越顯著，B/r0趨于0時，河道形態也趨于直河道，此時h2/H隨進占穩定在0.95～1.0，這與傳統的河道截流龍口水面線變化規律相符。

2.2.2 非淹沒流條件下

對于非淹沒流的情況通常發生在龍口束窄程度很大的時候，通過熊毅等[5]的分析計算可知此時龍口軸線水深相對較低，龍口流態為急流，落差主要集中在龍口軸線附近，可以預見彎道截流的雙龍口效應在非淹沒流條件下要比淹沒流顯著。非淹沒流下，小龍口相對水深h2/H～M關系曲線如圖7所示，雙龍口水深比h/h2～M的關系曲線如圖8所示。戧堤進占至截流最困難階段時，當M在0.2～0.1時，h2/H約為0.9～0.7，h/h2約為0.55～0.8，顯然在此區間段內小龍口水深變化非常明顯，水面線在小龍口處大幅度跌落，小龍口承擔相當一部分落差，彎道截流雙龍口效應顯著。非淹沒流條件下彎道相對河寬B/r0對雙龍口效應的影響更為顯著，B/r0在0.33～0.67時，雙龍口水深比在0.02～0.06內變化。

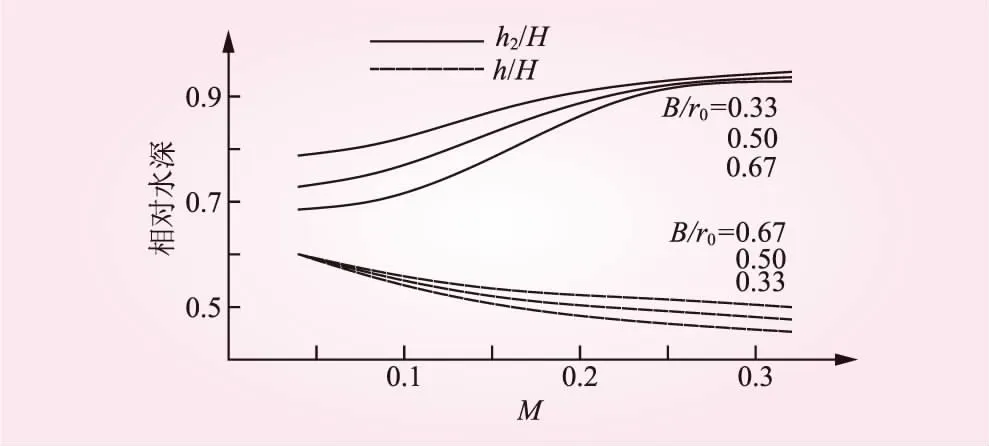
圖7 非淹沒流條件下雙龍口相對水深隨進占的關系

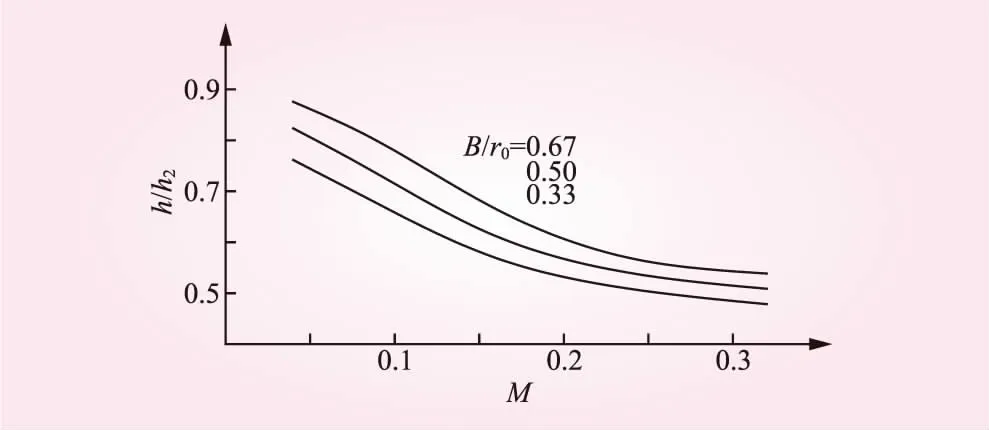
圖8 非淹沒流條件下雙龍口水深比隨進占的關系

僅從水流水面線的角度上分析，彎道截流在進占至一定區間后，戧堤上游坡腳至彎曲岸坡處河道顯著收縮，形成小龍口，使該處水面線跌落，與龍口共同承擔截流落差；水流至小龍口處較為平順的進入龍口，從一定程度上改善了龍口的水流流態，有助于降低截流龍口水力指標。

2.3 彎道形態對龍口流速的影響

對于龍口過水斷面為梯形斷面的條件下，龍口過流可視為寬頂堰自由溢流[6]，根據能量方程可求得龍口流速為

(8)

式中，ZB為龍口戧堤軸線處的水位跌落，可由龍口軸線相對水深h/H求出；m為流量系數。

小龍口處的流速v2可按連續性方程，結合式(8)進行求解，即

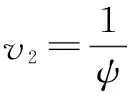
(9)

分析影響v2的因素可以采用單因素分析法，研究進占過程中σ和B/r0對小龍口水流流態的影響。取η=0.5、θ=60°、β0=1.0、ξ=0.2，對于淹沒流的情況，可取σ=0.1。雙龍口水流流速之比v2/v隨戧堤進占的關系曲線如圖9所示。

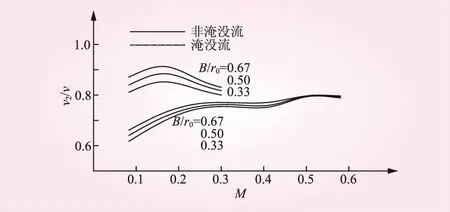
圖9 雙龍口水流流速之比隨進占的關系

對于淹沒流條件，隨進占的變化v2/v在0.6～0.8內變動，考慮到截流龍口流速的變化規律，在最困難時段流速達到最大，其值一般為進占剛開始時流速的5倍左右，因此對于小龍口的水流流速變化在M為0.15～0.25間達到最大，v2/v約為0.7；在M達到0.1后，v2/v開始明顯下降，這是由于此時龍口戧堤形成了三角形斷面，龍口的泄水能力顯著降低，同時龍口處水深較大，影響龍口前水流流態，使小龍口斷面水流較平穩，流速相對較小。

對于非淹沒流條件，隨進占的變化v2/v在 0.8～0.9范圍內變動，并于M為0.15附近時達到最大，考慮到該龍口束窄程度下截流位于最困難階段，此時小龍口處的水流流速極大。不同彎道相對河寬B/r0對小龍口水流流速有一定的影響，當B/r0在0.33～0.67時，v2/v在0.01～0.05內變化；彎道相對河寬越大，小龍口處水流流速也越大。

從水流流速的角度上分析，彎道截流在進占至一定區間后形成小龍口，該處由于束窄水流流速值較大，特別是在截流最困難階段，小龍口處流速非常接近龍口流速，會使水流在龍口前對戧堤堤頭坡腳進行顯著的沖刷。因此，彎道截流形成的雙龍口效應有利也有弊，既分擔了一部分龍口落差，降低截流水力指標，同時也會加大水流對堤頭的沖刷，實際工程施工設計中需要綜合考慮。

3 物理模型試驗分析

試驗采用動床正態模型，按重力相似準則設計，模型長度比尺為1∶60，模型制作范圍選定上游圍堰軸線以上約500 m，下游圍堰軸線以下約800 m，總長約1 800 m。動床范圍以保證河道沖淤相似為原則，從上游圍堰軸線上游約100 m開始到上游圍堰軸線下游約200 m處，總長約300 m。模型平面布置如圖1所示，戧堤布置在彎道出口末端，彎道彎角為35°，相對河寬B/r0取0.33。

通過模型試驗觀測，由于龍口位于岸坡處，水流以一定夾角流向龍口，在龍口寬一定范圍內，戧堤堤頭上坡腳與彎曲河道岸坡間束窄程度很小，甚至小于龍口束窄程度，收縮段改變了水流特性和流態，并承擔一部分落差，起到和龍口相同的作用，可視為雙龍口截流，其實測流速落差結果如表1所示，理論計算與模型試驗實測數據對比如表2所示。

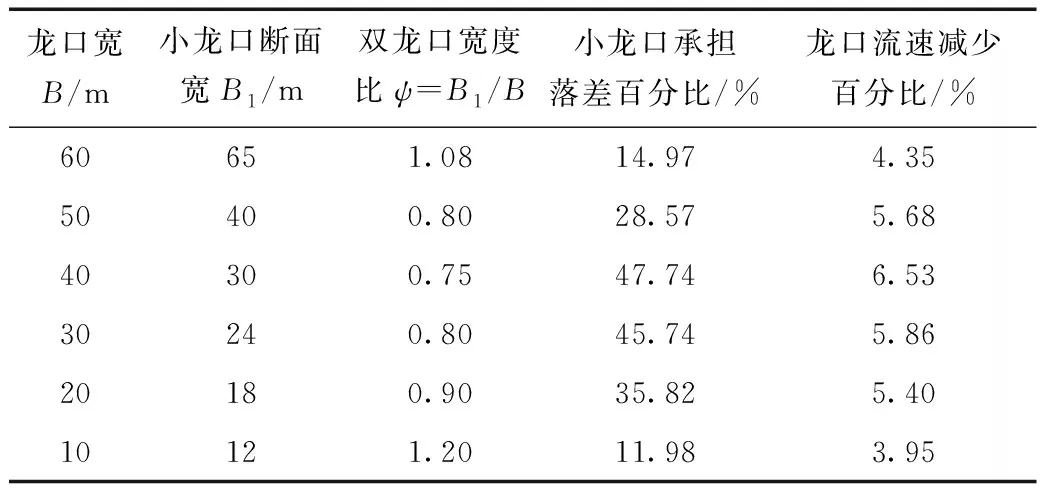
表1 雙龍口截流流速落差實測數據

表2 理論計算與模型試驗得到的流速水位對比

在龍口寬30～50 m間，龍口前收縮最為明顯，相應承擔的落差可達到總落差的47.74%，很大程度上降低了龍口段的截流指標。但龍口前束窄段水流收縮，流速增大，導致水流對基坑沖刷加重，特別是對進占端頭有很大淘刷作用，沿著戧堤進占端頭至河道形成一條沖溝。

從以上計算分析可知，工程實測資料與本文模型計算值較為接近[7- 8]，計算誤差范圍在3%～10%，考慮到本文模型建立在若干假設基礎上，模型計算理論是比較合理的，具有較好的適用性。

4 結 論

(1)通過試驗觀察和分析計算，提出彎道截流下出現雙龍口現象。以龍口軸線水深關系為基礎，建立雙龍口截流局部水深和流速計算模型，分析了彎道截流下龍口與小龍口處平均流速、軸線水深之比隨彎道相對河寬、彎道彎角、龍口束窄系數及淹沒程度的變化關系。分析結果表明，彎道截流在進占至一定區間后形成小龍口，小龍口承擔較大落差，一定承擔上降低龍口處的水力指標；彎道彎曲程度越大，雙龍口效應越明顯。

(2)通過與物理模型試驗的對比，驗證了彎道截流下雙龍口效應。為類似于丹巴水電站彎曲河道截留的工程充分考慮河床地基和岸坡的抗沖刷能力，合理的設計截流戧堤布置形式，使截流難度達到可控范圍提供了參考。

[1] 熊毅, 吳威, 陸賀, 等. 丹巴水電站上游河道岸坡對截流龍口水力參數的影響分析[J]. 水力發電, 2013, 39(12): 49- 53．

[2] 肖煥雄. 施工水力學[M]. 北京： 水利電力出版社, 1992．

[3] MA Jiming, LIU Tianxiong, LIANG Yanbo. The Three Gorges power intakes and their hydraulic properties[J]. Journal of Basic Science and Engineering, 2000, 8(3): 61- 68．

[4] 張洪武, 呂昕. 彎道水力學[M]. 北京: 水利電力出版社, 1993．

[5] 熊毅, 胡志根, 陸賀, 等. 彎曲河道立堵截流龍口水力特性分析[J]. 水利學報, 2017, 48(2): 184- 192．

[6] TULLIS B P, YOUNG J C, CHANDLER M A. Head-discharge relationships for submerged labyrinth weirs[J]. Journal of Hydraulic Engineering, 2007, 133(3): 248- 254．

[7] 寧晶, 張津, 寧廷俊. 三峽工程明渠截流龍口護底模型試驗與原型對比[J]. 水力發電學報, 2009, 28(2): 106- 109．

[8] SCHMOCKER L, HOCH E, MAYOR P A, et al. Hydraulic model study of the fuse plug spillway at Hagneck Canal, Switzerland[J]. Journal of Hydraulic Engineering, 2013, 139(8): 894- 904．