基于ARM的混沌幀同步系統設計與實現

楊曉云，徐強，莊燕濱

(常州工學院計算機信息工程學院，江蘇 常州 213032)

0 引言

序列密碼系統的特點是加密與解密使用同樣的密鑰，圖1為以混沌信號為密鑰的序列密碼系統原理圖。該系統發端，將欲發送的明文序列與混沌序列密鑰經模2加形成密文序列，通過信道將其傳送到收端。收端用與發端完全相同的混沌序列密鑰和發端傳送來的密文序列進行模2加，即可得到與發端相同的明文序列信號。

根據混沌信號產生原理，收發雙方采用相同的產生電路、相同的初始值和步長，便能得到相同的混沌序列密鑰。關鍵是收端的序列密鑰起始點，一定要對準發端密文序列的起始點，即二者要完全同步，才能通過模2加解密出正確的明文序列[1-4]。混沌信號同步包括位同步與幀同步兩部分。位同步即定時同步、碼元同步，通常采用數字鎖相環法來完成，其硬件實現亦比較容易[5-7]。本文主要討論混沌信號的幀同步系統的實現，它是在位同步建立后進行，即系統的收端時鐘與發端時鐘已經同步。圖2為本文提出的混沌信號幀同步方法的混沌序列密碼實驗系統原理圖。

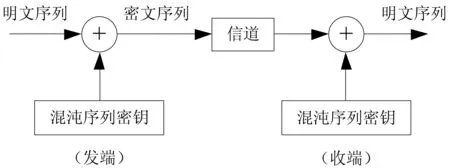
圖1 以混沌信號為密鑰的序列密碼系統原理圖

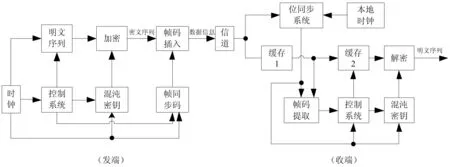
圖2 混沌序列密碼實驗系統原理圖

1 混沌信號同步發端實驗系統

本實驗系統的混沌序列密鑰采用文獻[8]中的混沌信號產生方法組成，即選用Lorenz系統的混沌電路，取迭代步長h=0.001和初始值(x0,y0,z0)=(1,1,1)，用C語言設計基于芯片STM32F103VET6的運行程序進行運算，圖3為其程序流程圖。

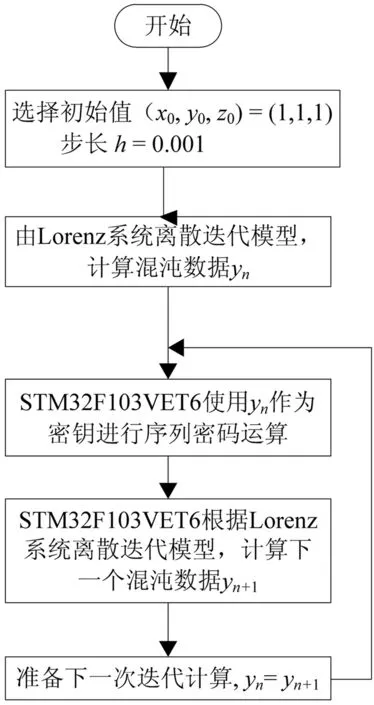
圖3 混沌序列密鑰程序流程圖

取產生的混沌序列的前256 bit(3FF0000000000000，3FF000B242070B8D,3FF00213A0C6B485，3FF004230FCF80DC)作為發端混沌序列密鑰。

幀同步碼型應選擇具有尖銳單峰特性的局部自相關函數的特殊碼組[9]。巴克碼是一種非周期序列，一個n位的巴克碼組為{x1,x2,x3,…,xn}，其中xi取值為+1或-1，其局部自相關函數為

(1)

本方案采用7位的巴克碼(1110010)，為了構成一個字節(8位碼)，再加一位監督碼“0”，便組成了幀同步碼(11100100)。為方便收端檢測與觀察，本方案的測試序列(即明文序列)，采用轉義字符組成與密鑰序列長度相等的一組序列(0708090A0B0C0D0E，22273E3F004A5B5C，000708090A0B0C0D，0E22273E4A5B5C3F)作為明文序列幀(由32個字節組成)，將其反復向收端傳送。

圖4為本方案的混沌信號同步發端實驗系統原理圖。具體工作過程：發端實驗系統在控制電路統一控制下進行工作，首先將明文序列與混沌序列密鑰進行模2加，形成一個密文序列幀，而后將幀同步碼加到此幀密文序列的開頭，構成數據信號序列，通過信道傳送到收端。圖5為發端數據信號時序示意圖。

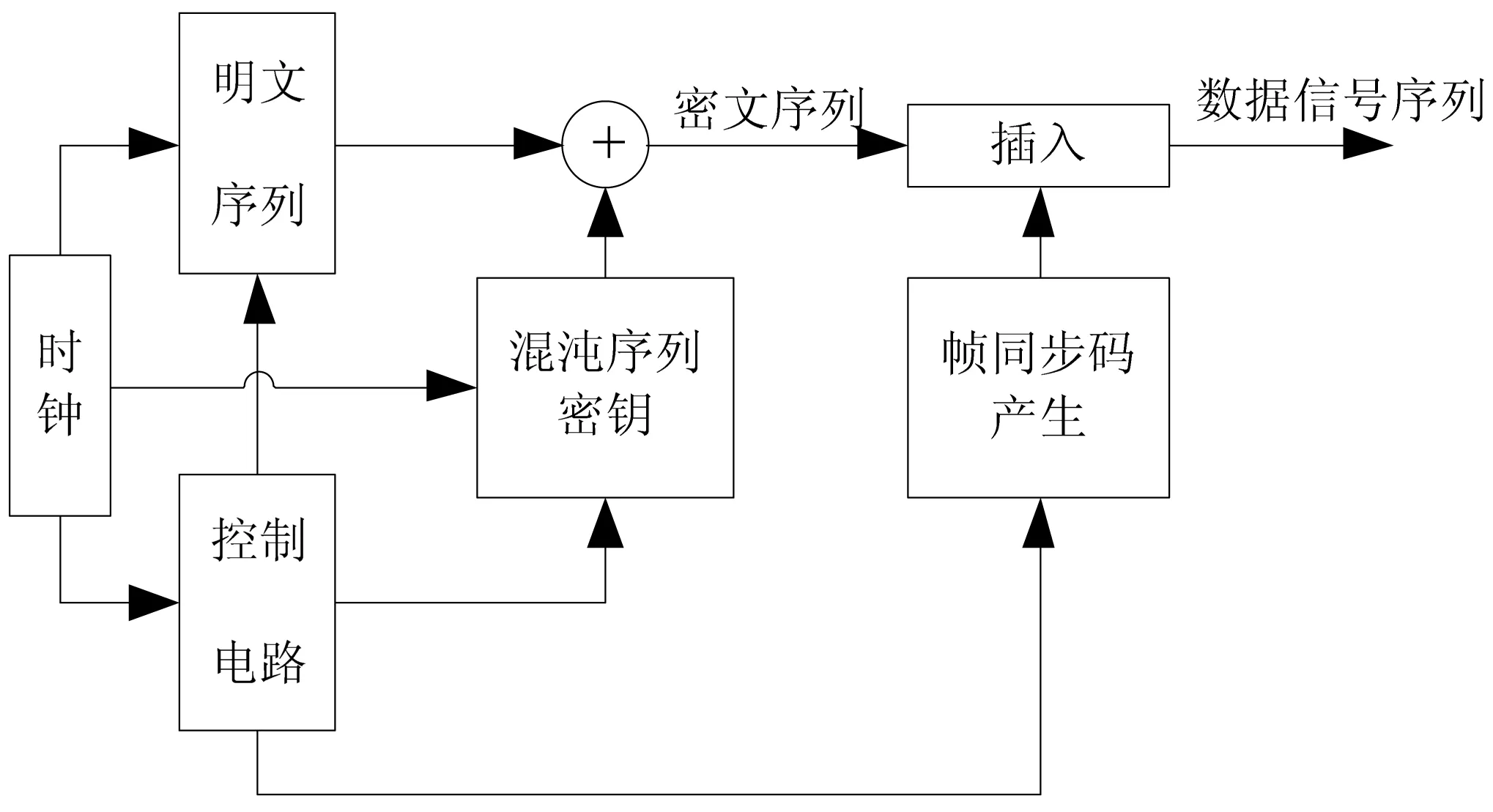
圖4 混沌信號同步發端實驗系統

圖5 發端數據信號時序示意圖

2 混沌信號同步收端實驗系統

收端為了從發端送來的數據信號中正確恢復出明文序列，收端的時鐘必須與所收到的發送時鐘信號同步，這由位同步系統實現。

位同步建立后，收端在控制電路統一管理下工作。幀同步系統立即從發端送來的數據信號中識別幀同步碼，即幀同步碼提取。為了防止數據信號序列中有可能存在與幀同步碼相同的碼，出現假同步，幀同步系統捕捉到第一個幀同步碼后，必須進行校驗，如果在下一周期同一位置上又提取到一個幀同步碼，這時才可以認為這個碼可能是幀同步碼。若設校驗次數n=1,便可認為此碼是幀同步碼，讓系統進入幀同步狀態。當然，為了減小假同步的概率，校驗次數可以增加，但同步建立時間就要加長。

收端根據發端規定的產生混沌序列密鑰的電路、初始值和步長，可以產生與發端完全一樣的混沌序列密鑰，存放在緩存器中，等待使用。當幀同步建立后，在控制電路管理下，準確地將數據緩存器中的數據信號序列與另一緩存器中的混沌密鑰序列同時取出，進行模2加，便可得到正確的明文序列。圖6為本方案的混沌信號同步收端實驗系統原理圖。

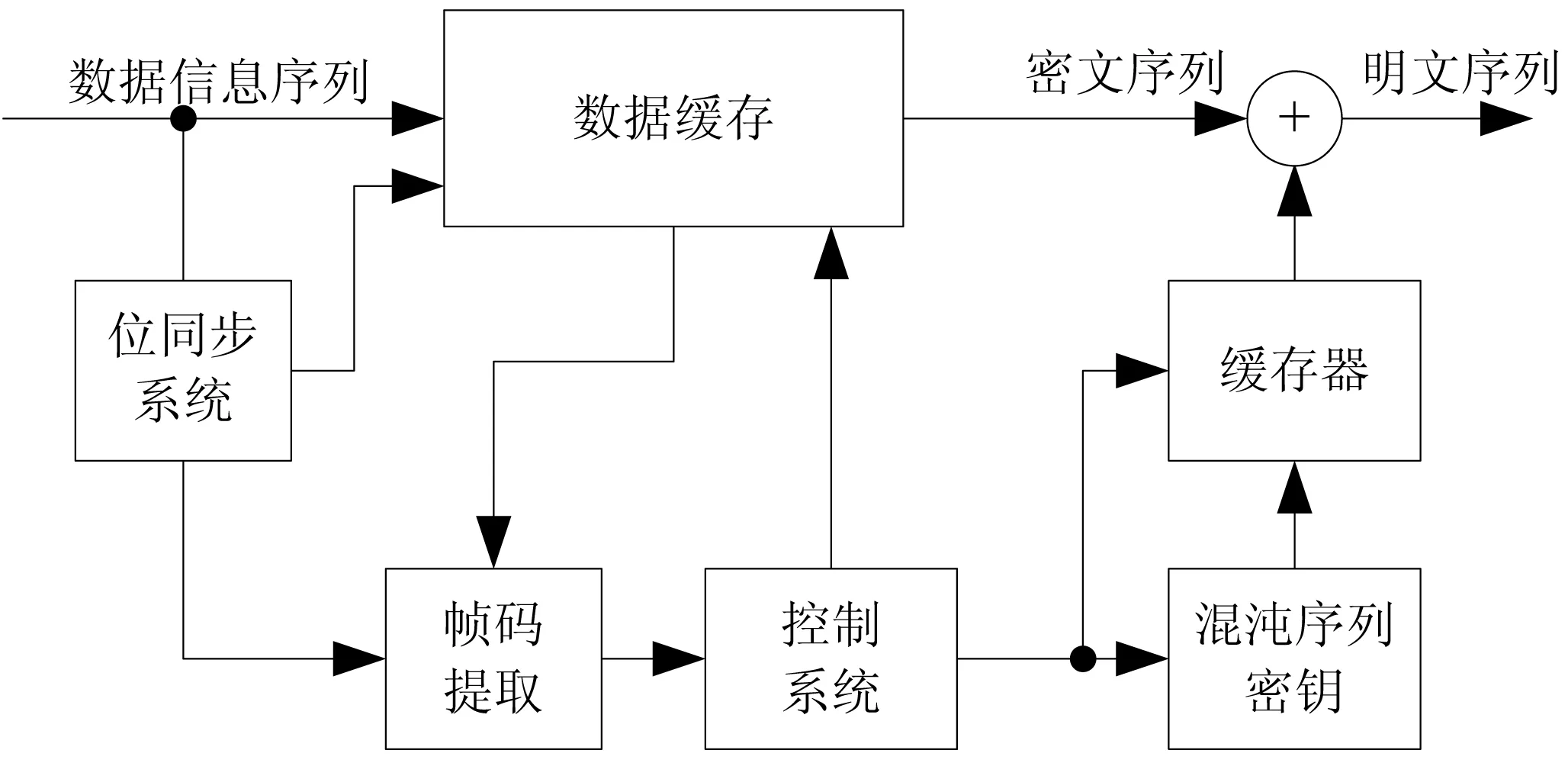
圖6 混沌信號同步收端實驗系統原理圖

本實驗系統亦采用STM32F103VET6芯片，主要包括混沌序列密鑰產生、控制電路及幀同步系統等模塊。

本實驗系統工作過程為，先將發端送來的數據信號經串/并變換后存貯在緩存器中，由幀同步比較器對送來的數據信息序列進行幀碼識別，當捕捉到一個幀碼(11100100)后，便進行校驗工作。本方案中校驗次數n=1，即如果捕捉到2個幀碼信號后，就確定系統進入同步狀態，便可識別出密文序列幀的起始點位置。通過控制電路從緩存器中將相應的密文序列送到解密器，此時將等待在那里的混沌密鑰序列亦送到解密器，讓二者對應進行模2加，便可得到正確的明文信號。

利用C語言將上述運算及各種處理對芯片STM32F103VET6進行編程，圖7為收端實驗系統的程序流程圖。

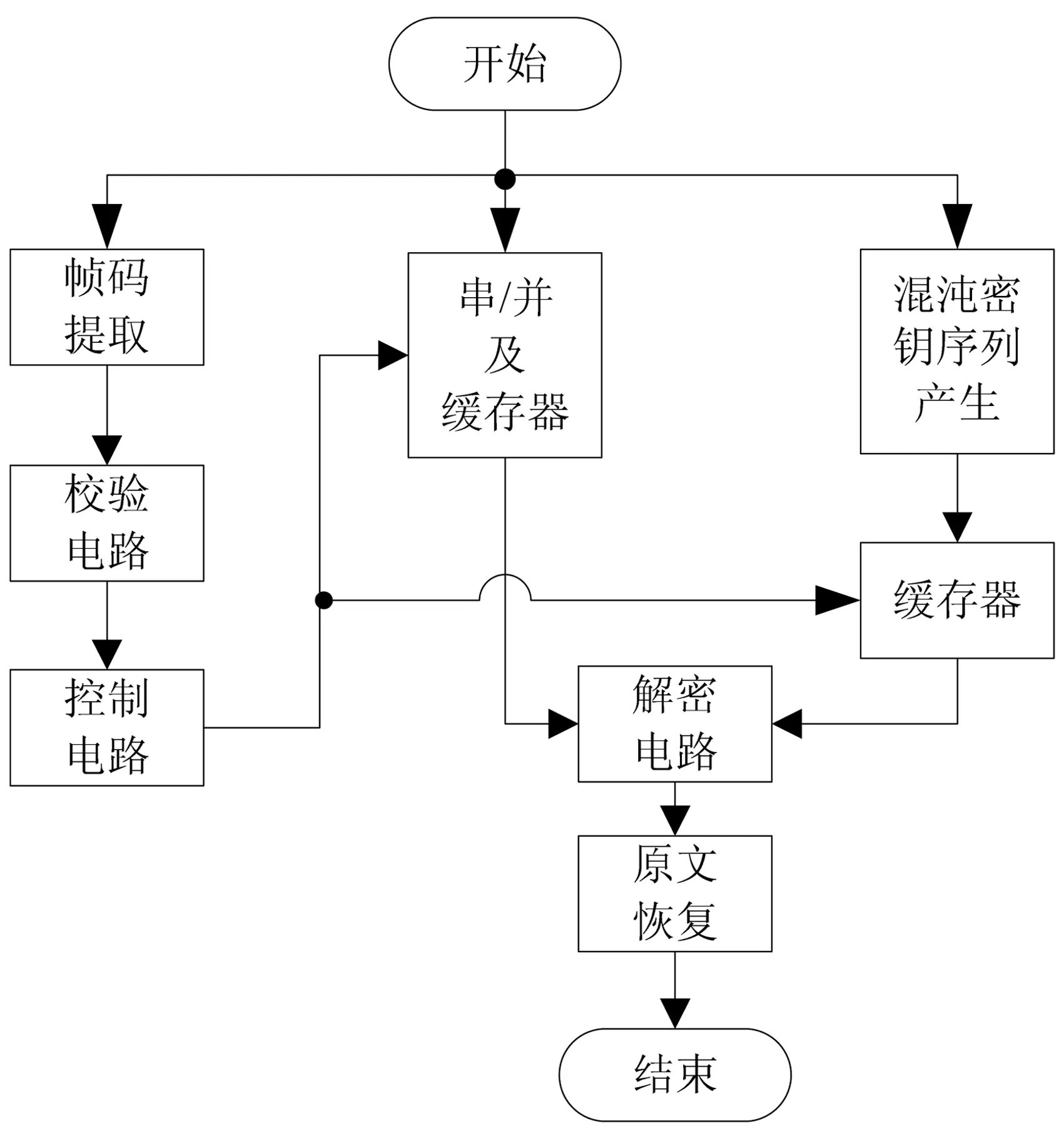
圖7 收端實驗系統程序流程圖

3 幀同步系統建立時間

從圖5數據時序圖可見，混沌數據信號序列與一般數據信號形式上是一樣的。位同步采用數字鎖相環方式，建立時間是很快的，因此整個系統建立時間主要取決于幀同步建立時間。幀同步系統從捕捉到同步建立需兩個階段：幀碼碼型信號識別和校驗階段。

明文序列每幀含m個字節，每個字節所占時間為TB。由于幀同步系統開始捕捉時可能在任何一個字節位置上，因此最慢識別到幀碼時間為mTB，最快為TB。故識別幀同步碼的平均時間TD為

TD=(m+1)TB/2

(2)

系統進入校驗階段后，有兩種情況。

第一種情況，設校驗次數為n，如果系統連續n次在同一位置上捕捉到幀同步碼，便可確定此碼組是真正的幀同步碼，讓系統進入同步狀態。

設位同步建立時間為TC，則系統總的建立時間TA為

TA=TC+TD+n(mTB)

(3)

第二種情況，為方便試驗，本文的測試信號序列采用由轉義字符組成的特殊序列作為明文序列。在實際應用中明文序列是隨機的，有可能存在與幀同步碼型一樣的碼組。若在接收到的數碼信息中存在與幀同步碼型一樣的碼組，系統捕捉到的可能是假幀同步碼，經校驗發現后，系統應立即重新捕捉，再校驗，直到捕捉到真正的幀同步碼，系統才可進入同步狀態。這時系統總的建立時間TA應該用下式來估算：

TA=TC+TD+n(mTB)+i(TD+mTB)

(4)

式中，i表示假同步次數。由于假同步最早可能出現在捕捉的第一次，最晚可能在校驗的第n次，故式(4)中i取平均值(i=n/2)。

由式(3)、(4)可見，幀同步系統建立時間長短與校驗次數n有很大關系，一般希望校驗次數n盡量選小一點。

4 結語

經測試，基于ARM的混沌信號同步實驗系統方案是可行的。由于混沌信號具有非周期性和類隨機噪聲等特性，很難對其進行跟蹤、分析和破解，其信息傳輸保密性是非常好的。但是混沌信號幀同步亦比較困難，尤其是硬件實現。本文提出這種混沌信號幀同步方法，硬件實現比較容易，性能也比較好，在使用混沌信號序列為密鑰的數字信封等技術中應用是很合適的。

[參考文獻]

[1]MAHERI Mahmoud,ARIFIN Norihan Md.Application adaptive exponential synchronization of chaotic dynamical systems in secure communications[J].Advances in Difference Equations,2017,96(1):1-21.

[2]李震波，唐駕時. 參數擾動下的混沌同步控制及其保密通信方案[J].控制理論與應用，2014,31(5)：592-600.

[3]李國華. 基于混沌導頻信號同步控制的混沌保密通信[J]. 計算機應用研究, 2014,31(9):2788-2790.

[4] 梅蓉，吳慶憲，陳謀，等. 時滯Lorenz混沌系統的同步電路實現及在保密通信中的應用[J]. 應用基礎與工程科學學報，2011,

19(5)：830-841.

[5]徐強，楊曉云，莊燕濱. 基于FPGA的高速光幕同步系統設計與實現[J].計算機測量與控制，2016,24(8)：294-297.

[6]杜勇，劉帝英，羅宇智.基于FPGA的改進積分型位同步環設計[J].信息技術，2013,37(5)：129-132.

[7]王永慶，喬媛，吳嗣亮. 基于早遲門位同步環的FPGA實現[J].微計算機信息，2009,25(8):178-179.

[8]楊曉云，徐強，莊燕濱. 基于混沌信號序列的數字信封[J].常州工學院學報，2016,29(2)：47-50.

[9]樊昌信，曹麗娜,等.通信原理[M].7版.北京：國防工業出版社，2013.