基于水波原理的城市道路交通事故影響分析
何雅琴,容煜倫,柳祖鵬
(武漢科技大學(xué)汽車與交通工程學(xué)院,湖北武漢430081)
城市道路交通事故不僅帶來生命和財(cái)產(chǎn)的損失,也會(huì)對(duì)城市交通系統(tǒng)造成一定的負(fù)面影響。如果事故點(diǎn)產(chǎn)生的排隊(duì)車輛不斷累積、疏散不及時(shí),將產(chǎn)生擴(kuò)散的連鎖反應(yīng),會(huì)導(dǎo)致大面積的交通擁堵甚至交通中斷。因此,對(duì)城市道路交通事故造成的影響進(jìn)行分析和研究并及時(shí)采取應(yīng)急對(duì)策,具有重要的理論意義和現(xiàn)實(shí)價(jià)值。目前對(duì)城市道路交通事故的影響分析主要以定性為主[1-3],定量的研究主要集中在事故影響范圍及持續(xù)時(shí)間方面,且研究方法主要為交通流理論[4-13],該理論基于流體力學(xué)理論,假設(shè)交通流處于密閉的空間。而城市道路網(wǎng)絡(luò)出入口、節(jié)點(diǎn)甚多,假設(shè)與實(shí)際情況差別較大。本文從城市路網(wǎng)實(shí)際特性出發(fā),探討城市道路交通事故的影響,為突發(fā)事件交通影響研究提供新思路。
1 城市道路交通事故影響定性分析
1.1 影響形式
1)點(diǎn)的影響。
當(dāng)路段上發(fā)生交通事故,事故點(diǎn)路段通行能力下降,瓶頸點(diǎn)形成,事故段交通開始出現(xiàn)混亂。此時(shí)若上游到達(dá)交通量小于事故后路段剩余通行能力,則不會(huì)引發(fā)交通擁堵排隊(duì),車輛會(huì)以較低的速度通過事故點(diǎn)。整個(gè)事故過程只對(duì)事故點(diǎn)的交通產(chǎn)生一定影響。
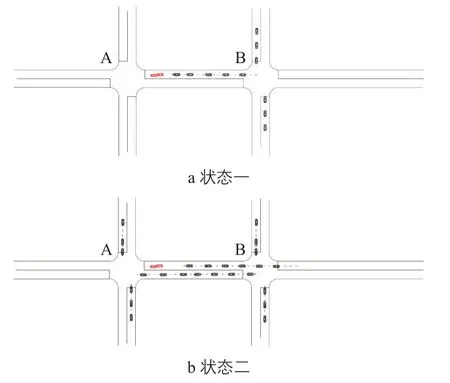
圖1 事故發(fā)生在有中間分隔帶路段的交通影響輻射Fig.1 Traffic impact radiation of accidents occurring on a roadway segment with median separator

圖2 事故發(fā)生在無中間分隔帶路段的交通影響輻射Fig.2 Traffic impact radiation of accidents occurring on a roadway segment without median separator
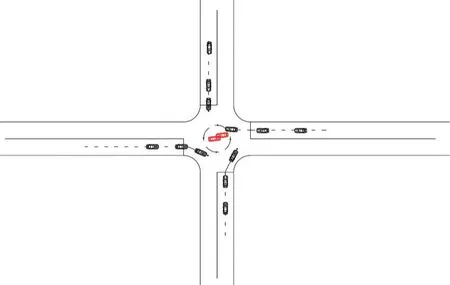
圖3 事故發(fā)生在交叉口的交通影響輻射Fig.3 Traffic impact radiation of accidents occurring within an intersection area
2)線的影響。
當(dāng)路段上發(fā)生交通事故,上游到達(dá)交通量大于事故后路段剩余通行能力,引發(fā)交通擁堵排隊(duì)。隨著擁堵的持續(xù),排隊(duì)長度逐漸延伸,整個(gè)路段處于擁堵狀態(tài),車流密度增大到極限。但是排隊(duì)尚未延伸到上游交叉口或者垂直交叉道路的交通量很小,暫時(shí)不會(huì)形成排隊(duì),事故只對(duì)其發(fā)生路段交通產(chǎn)生影響。
3)面的影響。
當(dāng)?shù)缆方煌ㄊ鹿拾l(fā)生后,排隊(duì)延續(xù)到上游交叉口,交叉口通行能力迅速下降,擁堵在上游交叉口開始向各個(gè)方向擴(kuò)散,造成更大范圍的交通擁堵,甚至使整個(gè)交通網(wǎng)絡(luò)陷入癱瘓狀態(tài)。
1.2 不同事故位置的影響范圍
1)有中間分隔帶的路段。
路段上發(fā)生如圖1所示的交通事故,會(huì)產(chǎn)生以下交通狀態(tài):①各車輛按規(guī)則有序行駛(見圖1a),由于交通事故使事故點(diǎn)通行能力明顯降低,形成一個(gè)虛擬瓶頸,事故后方到達(dá)車輛會(huì)減速或依次排隊(duì)等待,擁堵向上游蔓延,直至延伸到上游交叉口,上游交叉口各進(jìn)口道停車線后面的車輛也會(huì)受虛擬瓶頸影響,并使擁堵向四周擴(kuò)散;②車輛無序行駛(見圖1b),事故后方到達(dá)車輛依次減速或排隊(duì),并向上游蔓延伸展,上游交叉口B各方向車輛強(qiáng)行駛?cè)虢徊婵趽屝校瑢?dǎo)致交叉口內(nèi)車輛行駛混亂,使事故點(diǎn)對(duì)向車流在該交叉口受阻,進(jìn)而影響交叉口A的車輛正常行駛,以至影響周邊路網(wǎng)的交通運(yùn)行。
2)無中間分隔帶的路段。
路段上發(fā)生如圖2所示的交通事故,同樣會(huì)產(chǎn)生如下的交通狀態(tài):①不影響對(duì)向車輛正常行駛時(shí)借用對(duì)向機(jī)動(dòng)車道(見圖2a),由于事故后方車輛行駛軌跡發(fā)生變化,造成車輛減速,導(dǎo)致后方車輛排隊(duì),并向上游蔓延;②無序狀態(tài)下占用對(duì)向車道(見圖2b),使對(duì)向車流形成一個(gè)虛擬瓶頸,通行能力下降,造成對(duì)向車輛減速或排隊(duì),并向事故下游方向蔓延,事故對(duì)上下游方向的交通均產(chǎn)生影響,隨著持續(xù)時(shí)間的推移,車輛排隊(duì)會(huì)向四周蔓延,以至影響整個(gè)周邊路網(wǎng);③后續(xù)車輛按規(guī)則有序排隊(duì)等候,交通運(yùn)行情況與事故發(fā)生在有中間分隔帶的路段的狀態(tài)一相同。
3)交叉口內(nèi)部。
如圖3所示,當(dāng)事故發(fā)生在交叉口內(nèi)部,導(dǎo)致該交叉口的通行能力明顯降低,形成交通瓶頸,進(jìn)入交叉口各方向車輛會(huì)繞行事故點(diǎn),形成一個(gè)臨時(shí)環(huán)島交通,從而導(dǎo)致車速降低形成擁堵,并沿路段向四周蔓延,進(jìn)而影響周邊路網(wǎng)的交通運(yùn)行。
4)小結(jié)。
交通事故發(fā)生后無論是車輛有序行駛還是無序行駛,對(duì)交通影響的最終狀態(tài)均是以事故點(diǎn)為中心向四周逐漸擴(kuò)散的圓,輻射的范圍和速度與突發(fā)事件的嚴(yán)重程度相關(guān),且影響程度隨著與事發(fā)點(diǎn)距離的增大而逐漸減小。這與向水里扔石頭產(chǎn)生的漣漪現(xiàn)象一致,石頭扔進(jìn)水里會(huì)引發(fā)以石頭為圓心的水波,并以同心圓的形式向外傳播,傳播速度和傳播范圍與波源(石頭)的強(qiáng)度有關(guān),并且振動(dòng)強(qiáng)度隨著距離的增大逐漸衰減直至消失。如果交通系統(tǒng)中交通條件、道路條件均相同,事故對(duì)交通的影響將是均勻地向四周輻射,與水波現(xiàn)象一致。但是由于交通系統(tǒng)的不確定性,其道路條件和交通條件不可能完全一樣,事故對(duì)交通的影響可以看成是交通波非均勻地向四周擴(kuò)散。因此,可以嘗試借助于水波原理分析突發(fā)事件對(duì)交通的影響。
2 城市道路交通事故交通影響定量分析
2.1 交通影響系數(shù)
將城市道路交通事故的影響程度用定量指標(biāo)交通影響系數(shù)表示,定義為事發(fā)時(shí)受影響路網(wǎng)內(nèi)道路某一斷面、某一點(diǎn)的平均車速與事發(fā)前該點(diǎn)平均車速的比值,用α表示。
如圖4所示,O點(diǎn)表示事件發(fā)生地點(diǎn),事件發(fā)生后t時(shí)刻半徑為r、極角為θ的斷面A上交通影響系數(shù)
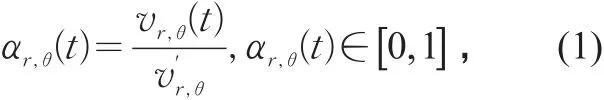
式中:r為事件影響范圍半徑/mt為事件的影響時(shí)間為事件發(fā)生后t時(shí)刻距事發(fā)地半徑為r、極角為θ的斷面的平均車速/(km·h-1);為事件發(fā)生前距事發(fā)地半徑為r、極角為θ的斷面的平均車速/(km·h-1)。α越大,交通影響程度越小,α越小,交通影響程度越大。αr,θ(t)=0表示影響達(dá)到極值,道路成阻塞狀態(tài);αr,θ(t)=1表示突發(fā)事件對(duì)交通沒有影響或影響已經(jīng)恢復(fù)。

圖4 基于水波原理的突發(fā)事件對(duì)交通的影響Fig.4 Impact of road accidents based on water wave theory
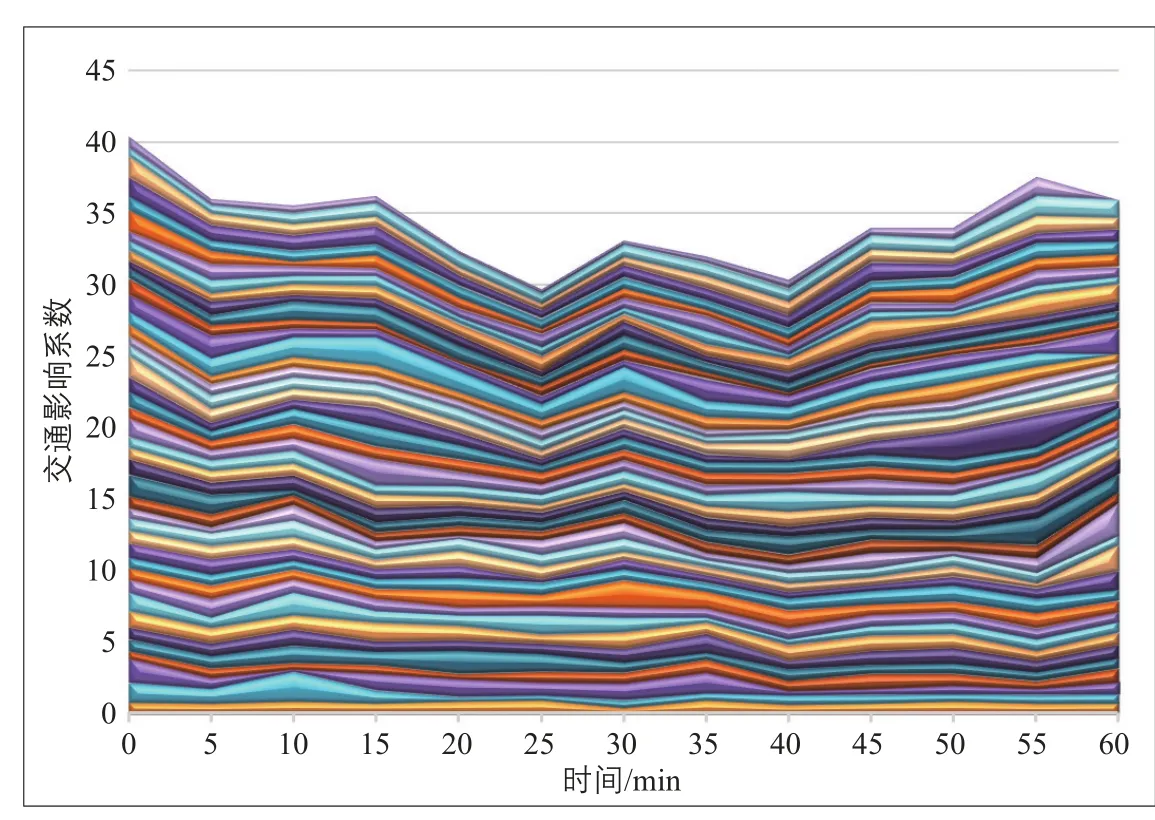
圖5 交通影響系數(shù)變化趨勢(shì)Fig.5 Trends of traffic impact coefficient
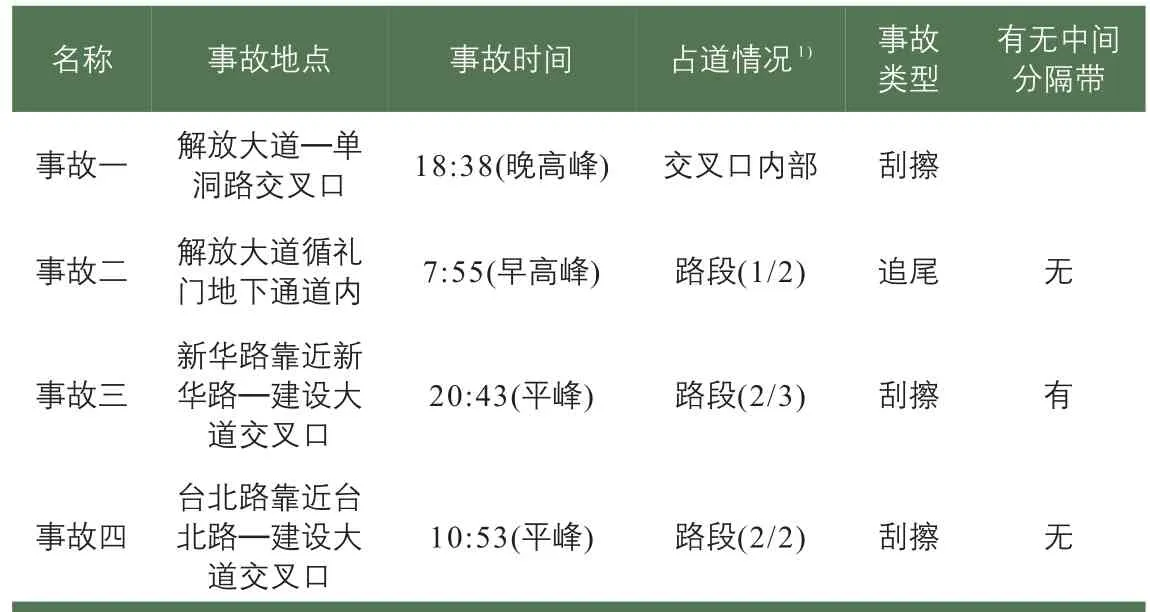
表1 不同交通事故特征Tab.1 Characteristics of different traffic accidents
2.2 交通影響系數(shù)特征分析
基于從交管部門調(diào)研獲得的交通事故和道路行車速度數(shù)據(jù),篩選造成交通擁堵較嚴(yán)重的42起事故,并對(duì)每一起事故的所有影響路段車速進(jìn)行整理,得到各影響路段在事故發(fā)生當(dāng)天的前后各5天6:00—22:00每5 min間隔的車速數(shù)據(jù)(見圖5)。為了反映事發(fā)前道路的正常運(yùn)行速度,取事發(fā)當(dāng)日前后共10天平均車速作為事發(fā)前車速,從而得到各個(gè)影響路段每5 min間隔的交通影響系數(shù)。在實(shí)際路網(wǎng)條件下,不是事件影響圈上每一個(gè)點(diǎn)都會(huì)對(duì)應(yīng)道路。另外,事件造成的影響是非均勻向外輻射的,即使同一半徑的單個(gè)圓環(huán),影響點(diǎn)也可以認(rèn)為是離散的。因此,暫時(shí)不考慮極角和半徑的影響,只考慮隨時(shí)間的變化。

圖6 事故影響點(diǎn)的交通影響系數(shù)Fig.6 Traffic impact coefficient at accident impact points
可以看出,各起交通事故的交通影響系數(shù)變化趨勢(shì)基本一致,都是先減小至某一點(diǎn),然后再逐漸增大,與事故發(fā)生后的交通運(yùn)行狀態(tài)吻合。事故發(fā)生后,交通運(yùn)行開始受到影響,直至影響達(dá)到最大,隨后由于交通疏導(dǎo)措施的介入,影響會(huì)逐漸減小直至消失。因此,本文用交通影響系數(shù)描述事故對(duì)交通的影響具有可行性。
選取4起代表不同特征的交通事故進(jìn)行詳細(xì)分析(見表1)。將每起事故各影響路段的交通影響系數(shù)隨時(shí)間變化值繪制成曲線(見圖6)。r為影響點(diǎn)與事故點(diǎn)的距離/m;u和d分別為影響點(diǎn)位于事故點(diǎn)的上游或下游。
由于交通系統(tǒng)的不確定性及各影響點(diǎn)位置不同,其開始受影響和恢復(fù)交通的時(shí)間也不盡相同,各曲線軌跡之間會(huì)存在一定的差異,但是整體變化趨勢(shì)基本一致。
從圖6中散點(diǎn)及曲線特征可以看出,曲線呈波浪線型,隨著時(shí)間的推移,交通影響系數(shù)先從1逐漸減小至最小值,再逐漸增大直至接近1①,該曲線與水波波面?zhèn)鞑デ€形狀類似(見圖7)。圖7波形函數(shù)可表示為

式中:η為波高/m;H為波幅/m;k為2π時(shí)間范圍內(nèi)波的起伏震動(dòng)次數(shù);x為橫、縱距離/m;σ為圓頻率;t為傳播時(shí)間/s;T為周期。
為了使公式(2)具有一般性,可以改寫為三角函數(shù)
式中:A為波高,即波峰的縱坐標(biāo)值;W為公式(2)中的k,W=2π/T;C為圖像沿x軸水平平移的距離;D為波離開坐標(biāo)軸的距離。
從圖6的曲線軌跡還可以看出,與事發(fā)地點(diǎn)越遠(yuǎn)的影響點(diǎn),其交通影響系數(shù)變化越快,事故剛發(fā)生時(shí),距事故點(diǎn)遠(yuǎn)的影響點(diǎn)的交通影響系數(shù)會(huì)先達(dá)到最低點(diǎn),隨后,交通開始恢復(fù)時(shí),其影響系數(shù)會(huì)率先達(dá)到或接近1,意味著會(huì)比離事發(fā)地點(diǎn)近的影響點(diǎn)先恢復(fù)交通。這與實(shí)際交通運(yùn)行狀態(tài)一致。
2.3 交通影響系數(shù)建模
為了驗(yàn)證交通影響系數(shù)隨時(shí)間變化特征能否用水波方程描述,以事故一為研究對(duì)象,將對(duì)應(yīng)事故發(fā)生后各個(gè)時(shí)刻(5 min間隔)的所有影響路段(也稱影響點(diǎn))的影響系數(shù)進(jìn)行平均,得到α和t的散點(diǎn)圖(見圖8)。利用SPSS統(tǒng)計(jì)軟件對(duì)該圖像進(jìn)行擬合,建立α與t的關(guān)系模型,選用類似水波方程的公式(4)進(jìn)行模擬。
在SPSS中進(jìn)行非線性回歸時(shí),需要手動(dòng)輸入自變量和因變量以及模型公式,還需要對(duì)模型中的參數(shù)進(jìn)行初始值的賦予。初始值的賦予力求滿足模型的特征,即減少迭代次數(shù),讓模型能夠更好地滿足數(shù)據(jù)要求。首先輸入公式(4),然后再逐步輸入各參數(shù)初始值,結(jié)合圖8,賦予A初始值為0.2,W初始值為0.079(周期取80 min),C初始值為5.0,D初始值為0.7,迭代結(jié)果見表2和表3,得到關(guān)系模型

利用水波方程模擬交通影響系數(shù)隨時(shí)間的關(guān)系擬合程度較好(R2=0.948),具有一定的統(tǒng)計(jì)意義,同時(shí)也符合實(shí)際交通特性。因此,利用水波原理分析城市突發(fā)事件的交通影響具有可行性。

圖7 水波自由面示意Fig.7 Water wave surface
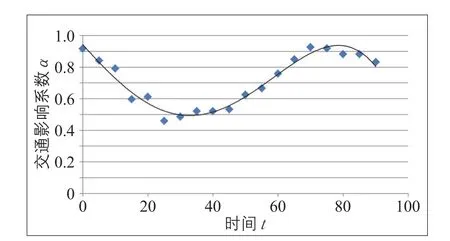
圖8 平均交通影響系數(shù)特征Fig.8 Characteristics of average traffic impact coefficient

表2 實(shí)際事故數(shù)據(jù)迭代歷史記錄Tab.2 Iteration historic records of real accidents
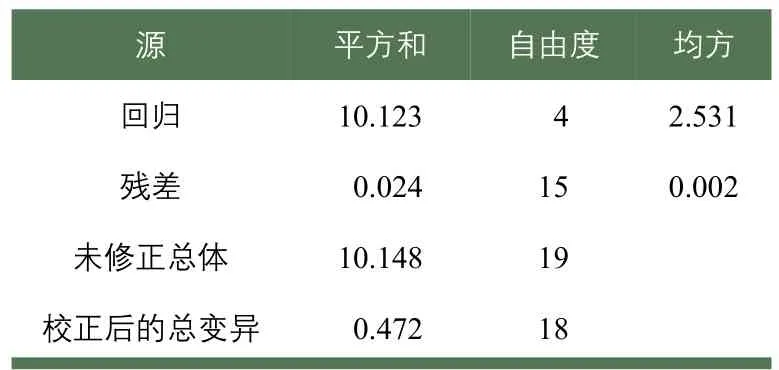
表3 實(shí)際事故數(shù)據(jù)方差分析Tab.3 ANOVAanalysis using real accidents dataset
2.4 仿真分析
2.4.1 仿真場(chǎng)景
假設(shè)某個(gè)有中間分隔帶的雙向10車道路段上發(fā)生一起兩車刮擦事故,占用2個(gè)車道,事故延遲時(shí)間為20min。對(duì)該事故進(jìn)行VISSIM仿真,采用信號(hào)控制模擬交通事故的發(fā)生,總周期為4 200 s,共設(shè)置三組,以便體現(xiàn)事故車輛占用的道路長度:0~1 200 s為綠燈,表示事故發(fā)生前的時(shí)間;1 200~2 400 s為紅燈,代表事故時(shí)間;2 400~4 200 s為綠燈,表示事故結(jié)束。仿真運(yùn)行示例見圖9。在事故周邊路段設(shè)置數(shù)據(jù)采集點(diǎn),獲取通過各斷面的車速數(shù)據(jù)。
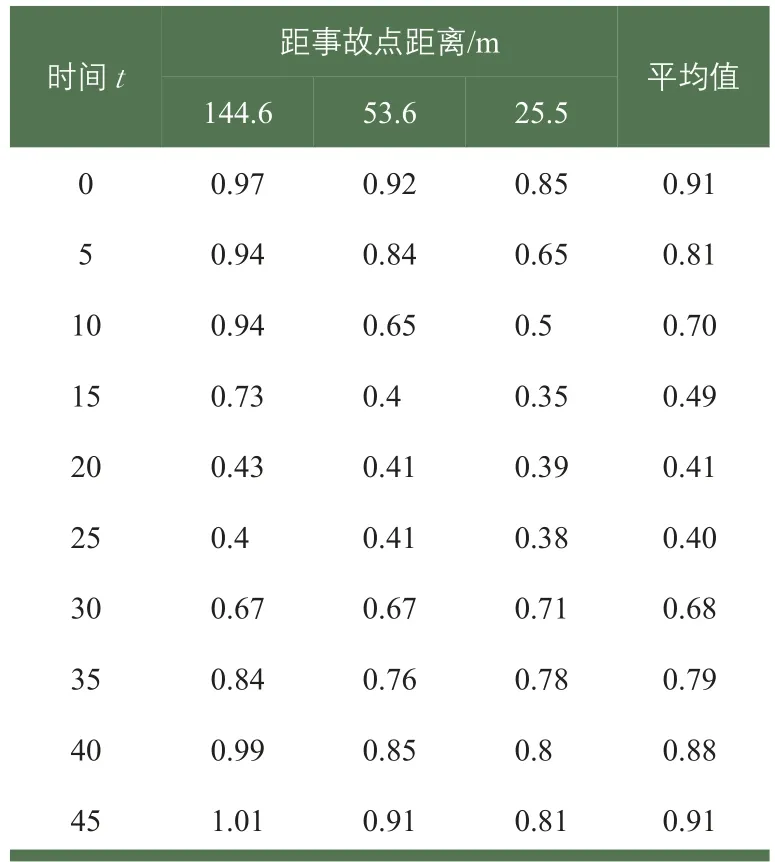
表4 交通影響系數(shù)α仿真結(jié)果Tab.4 Simulation results of traffic impact coefficientα
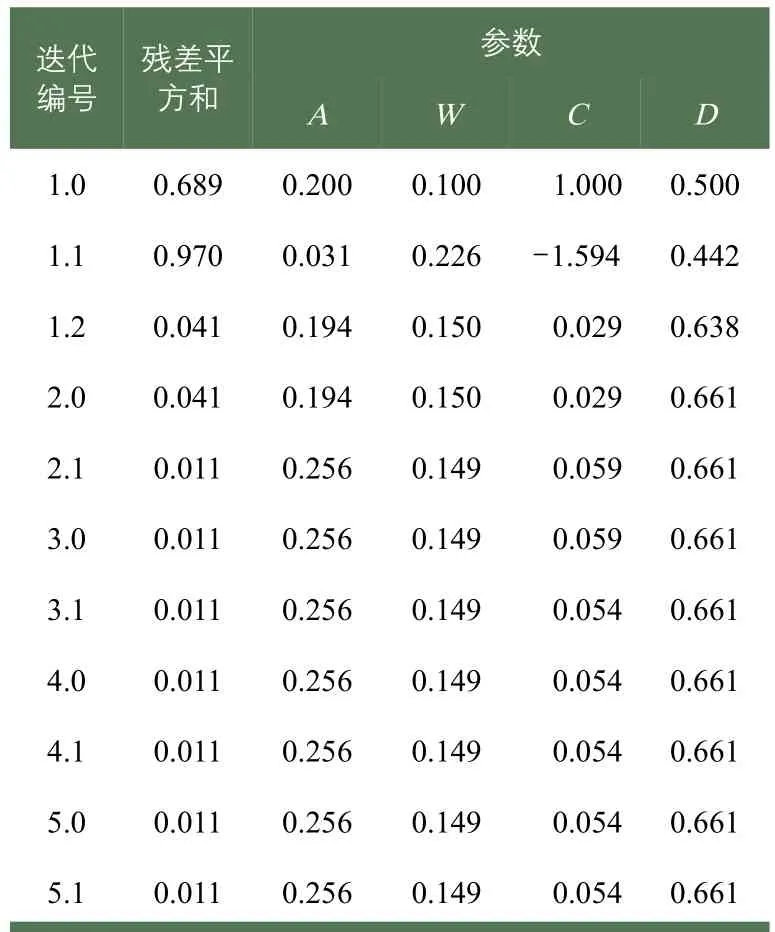
表5 仿真事故數(shù)據(jù)迭代歷史記錄Tab.5 Iteration historic records of simulated accidents

表6 仿真事故數(shù)據(jù)方差分析Tab.6 ANOVAanalysis using simulated accidents dataset
2.4.2 交通影響系數(shù)分析
根據(jù)仿真輸出的事故前后車速值,計(jì)算事故點(diǎn)周邊3個(gè)斷面每5 min間隔的交通影響系數(shù)(見表4)。
根據(jù)公式(5)構(gòu)建的模型,利用SPSS軟件對(duì)交通影響系數(shù)α和時(shí)間t進(jìn)行回歸分析,結(jié)果見表5、表6及公式(6)。
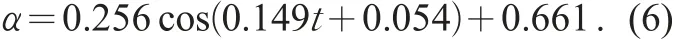
利用仿真所得數(shù)據(jù)構(gòu)建的交通影響系數(shù)α與時(shí)間t的關(guān)系模型,進(jìn)一步證明了水波原理用于突發(fā)事件交通影響分析的可行性。
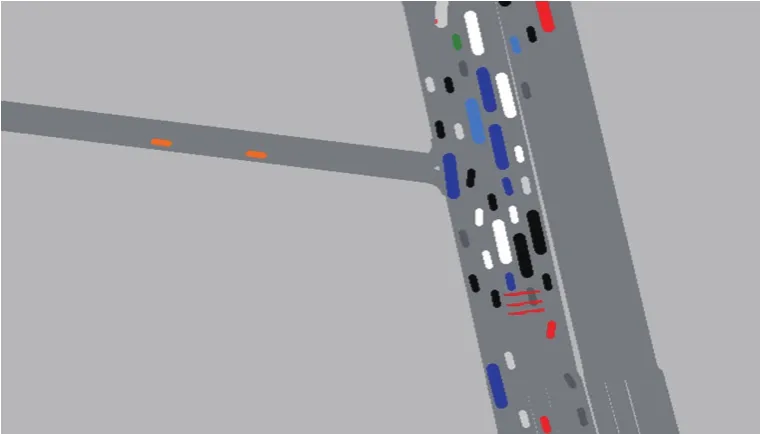
圖9 仿真運(yùn)行示例Fig.9 Simulation demo example
3 結(jié)論
本文首先定性分析城市道路交通事故的交通影響,并與水波現(xiàn)象進(jìn)行對(duì)比分析;在此基礎(chǔ)上,提出交通影響系數(shù)概念,并繪制交通影響系數(shù)隨時(shí)間變化的曲線,發(fā)現(xiàn)該曲線與水波波面曲線形式一致,且符合實(shí)際交通運(yùn)行規(guī)律。借助水波波動(dòng)方程,構(gòu)建交通影響系數(shù)隨時(shí)間的關(guān)系模型,最后利用仿真數(shù)據(jù)對(duì)模型進(jìn)行驗(yàn)證。結(jié)果表明,模型擬合度較好,具有統(tǒng)計(jì)意義。因此,用水波原理分析交通事故的交通影響,可以為突發(fā)事件交通影響研究提供一個(gè)嶄新的平臺(tái)和思路。
由于采集數(shù)據(jù)有限,出現(xiàn)了某些交通影響系數(shù)值大于1的情況,與理論值有偏差。另外,本文僅對(duì)代表不同事故場(chǎng)景的4起事故進(jìn)行分析,無法全面反映各種類型交通事故,具有一定的局限性。交通事故影響定性分析時(shí)在建模過程中存在一些假設(shè),并且只驗(yàn)證了模型的形式。因此,對(duì)于模型的精確性及實(shí)際應(yīng)用還有待后續(xù)的深入研究和驗(yàn)證。
注釋:
Notes:
①曲線中部分距離事發(fā)地較遠(yuǎn)的影響點(diǎn)在事故開始和結(jié)束時(shí)的交通影響系數(shù)出現(xiàn)大于1的情況,一方面是這些影響點(diǎn)受影響開始時(shí)刻有延遲及提前恢復(fù)交通,另一方面車速除了受交通事故影響外還會(huì)受很多其他因素的影響,可能使事故當(dāng)天某個(gè)時(shí)段(正好是事故剛發(fā)生時(shí))的車速比平時(shí)同一時(shí)段高,從而造成實(shí)際值大于1,與理論值存在一定的偏差。
:
[1]陳燕.應(yīng)對(duì)突發(fā)事件的城市交通應(yīng)急管理研究[D].成都:西南交通大學(xué),2009.Chen Yan.Research on Urban Traffic Emergency Management for Coping with Emergency[D].Chengdu:Xi'nan Transportation University,2009.
[2]石超峰,徐寅峰.突發(fā)事件對(duì)交通網(wǎng)絡(luò)的影響評(píng)估指標(biāo)和方法[J].運(yùn)籌與管理,2013,22(4):144-150.Shi Chaofeng,Xu Yinfeng.Link Importance Identification of Transportation Networks in the Emergency[J].Operations Research and Management Science,2013,22(4):144-150.
[3]張臣軍,王振山,高原.剮蹭事故對(duì)交通運(yùn)行的影響評(píng)估分析[J].道路交通與安全,2011,11(1):46-50.Zhang Chenjun,Wang Zhenshan,Gao Yuan.Analysis and Evaluation on the Traffic Operation Influence of Accident[J].Road Traffic and Safety,2011,11(1):46-50.
[4]Baykal-Gürsoy M,Xiao W,Ozbay K.Modeling Traffic Flow Interrupted by Incidents[J].European Journal of Operational Research,2009(195):127-138.
[5]Chien S J,Goulias D G,Yahalon S,et al.Simulation-Based Estimates of Delays at Freeway Work Zones[J].Journal of Advanced Transportation,2002,36(2):131-156.
[6]余貴珍,劉玉敏,金茂菁,等.基于交通波的高速公路事故的交通影響分析[J].北京航空航天大學(xué)學(xué)報(bào),2012,38(10):1420-1424.Yu Guizhen,Liu Yumin,Jin Maojing,et al.Traffic Impact Analysis of Highway Accident Based on the Shockwave Theory[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(10):1420-1424.
[7]俞斌,陸建,陶小伢.道路交通事故的影響范圍算法[J].城市交通,2008,6(3):82-86.Yu Bin,Lu Jian,Tao Xiaoya.Method to Determine the Influence Area of Street Accidents[J].Urban Transport of China,2008,6(3):82-86.
[8]孫明玲,楊峰,貝登榮,等.基于交通波動(dòng)理論的排隊(duì)消散時(shí)效分析[J].公路交通科技,2013,30(10):112-116.Sun Mingling,Yang Feng,Bei Dengrong,et al.Analysis of Queue Dissipation Time Effect Based on Traffic Wave Theory[J].Journal of Highway and Transportation Research and Development,2013,30(10):112-116.
[9]馬劍,李文勇,梁滿朝.基于卡爾曼濾波的交通突發(fā)事件影響范圍預(yù)測(cè)研究[J].長沙大學(xué)學(xué)報(bào),2012,26(5):86-89.Ma Jian,Li Wenyong,Liang Manchao.Predictionof TrafficEmergencyImpactScope Based on Kalman Filerting[J].Journal of Changsha University,2012,26(5):86-89.
[10]胡曉健,王煒,陸建.道路交通意外事件影響范圍確定方法[J].東南大學(xué)學(xué)報(bào)(自然科學(xué)版),2007,37(5):934-939.Hu Xiaojian,Wang Wei,Lu Jian.Determination Impact Area of Traffic Incident[J].Journal of Southeast University(Natural Science Edition),2007,37(5):934-939.
[11]張貴賓,劉清,嚴(yán)新平.高速公路緊急事件延誤影響分析[J].公路,2008(10):120-123.Zhang Guibin,Liu Qing,Yan Xinping.Analysis of Impact of Expressway Emergencies on Traffic Delay[J].Highway,2008(10):120-123.
[12]叢浩哲,王俊驊,童世鑫.高速公路網(wǎng)絡(luò)交通突發(fā)事件輻射范圍預(yù)測(cè)模型[J].同濟(jì)大學(xué)學(xué)報(bào)(自然科學(xué)版),2012,40(3):414-422.Cong Haozhe,Wang Junye,Tong Shixin.Prediction Model of Freeway Network Traffic Incident Radiation Scope[J].Journal of Tongji University(Natural Science),2012,40(3):414-422.
[13]曹志遠(yuǎn),郭忠印,張起森,等.高速公路重大交通事故時(shí)空影響范圍研究[J].公路工程,2011,36(6):55-58+73.Cao Zhiyuan,Guo Zhongyin,Zhang Qisen,et al.Research on Time and Spatial Extent of Terrible Traffic Accident on Highway[J].Highway Engineering,2011,36(6):55-58+73.

