梯度磁場中自旋-軌道耦合旋轉兩分量玻色-愛因斯坦凝聚體的基態研究?

李吉 劉伍明

1 引 言

兩分量玻色-愛因斯坦凝聚體(BEC)[1,2],由于組分內相互作用與組分間相互作用兩者互相競爭,為我們提供了一個全新的量子平臺,可以研究許多有趣的拓撲缺陷[3?13].實驗方面,Matthews等[2]在兩分量BEC中產生了量子渦旋.Anderson等[3]觀察到暗孤子在動力學過程中被分解為渦旋環.理論方面,Kasamatsu等[4]發現兩分量BEC中的多疇是由調制不穩定性而形成的.Williams等[6]得到了多量子數渦旋.?hberg和Santos[7]研究了兩分量BEC中暗孤子的產生以及孤子間相互作用.一些研究者進一步詳細討論了旋轉勢下兩分量BEC中的新奇拓撲結構和基態相圖,例如四角渦旋晶格的動力學過程[9]、整數渦旋與分數渦旋的相變[10]以及不同渦旋結構的相圖[11].此外,Battye等[12]證實了在兩分量BEC中存在穩定的skyrmion結構.Martikainen等[13]理論研究了在兩分量BEC中產生磁單極結構的方法.近年來,隨著拓撲絕緣體和自旋霍爾效應的興起,自旋-軌道耦合的研究吸引了人們廣泛的關注.BEC由于其高度的可調控性,為實現和產生人造自旋-軌道提供了一個非常理想的平臺.人們已經在超冷原子氣體實驗中實現了一維和二維形式的自旋-軌道耦合[14?17].許多研究者也在理論上提出了不同的實現方案[18?26].人造自旋-軌道耦合 BEC,由于原子內部自旋態和質心運動的耦合,進而提供了更多的機遇探索新奇量子態[27?33].Wang等[27]在無外勢的自旋-軌道耦合兩分量BEC中發現了平面波相和條紋相.如果考慮外勢,體系將出現新的量子態,例如分數渦旋和渦旋格子[28]以及skyrmion格子[29].Bhat等[31]討論了自旋-軌道耦合對調制不穩定性的影響.Kato等[33]研究了自旋-軌道耦合 BEC中渦旋-反渦旋對的動力學性質,并且發現在該體系中渦旋-反渦旋對的運動速度更慢.緊接著,人們研究了旋轉勢下自旋-軌道耦合兩分量BEC的基態性質[34?44].例如,Xu和Han[34]在該體系中發現了對稱排列的渦旋列和中心伴有巨skyrmion的三角渦旋格子.Liu等[35]發現在兩分量BEC中自旋-軌道耦合能夠誘導環形-雙曲狀的skyrmion.Zhou等[36]探討了具有旋轉和自旋-軌道耦合兩分量BEC的基態性質,發現了半量子數渦旋格子結構.Fetter[42]詳細討論了自旋-軌道耦合BEC中的動力學行為.最近,人們利用磁場梯度實現了一些新奇量子態并觀察到量子相變過程.有研究者利用梯度磁場方法實現了光晶格體系中的量子霍爾效應[45].此外,在BEC中借助梯度磁場,實驗上觀察到了人造磁單極結構[46,47]和量子扭結[48,49].之前的工作研究了梯度磁場中三分量BEC的基態結構,例如伴隨極核渦旋的磁單極[50]和對稱性排列的渦旋格子[51].然而,在兩分量BEC中,梯度磁場和自旋-軌道耦合共同作用是否會導致新奇的基態結構和不同的基態相變,到目前為止這些問題依然不清晰.

本文研究了自旋-軌道耦合作用和梯度磁場對旋轉兩分量BEC基態的影響.研究結果表明,在梯度磁場中,隨著自旋-軌道耦合強度增大,基態結構由skyrmion格子逐漸過渡為沿著對角線方向排列的skyrmion列.通過改變磁場梯度強度大小,深入探索該調控參數對系統基態結構的影響.發現當自旋-軌道耦合強度和旋轉頻率都小,磁場梯度的增強可導致基態由平面波相轉變為half-skyrmion;當自旋-軌道耦合強度和旋轉頻率都大,梯度磁場可誘導hidden渦旋的產生.最后討論了不同基態的自旋構型.梯度磁場作為自旋-軌道耦合兩分量BEC中新的調控參數,能夠控制和實現不同基態相間的轉化.

2 理論模型

考慮梯度磁場和自旋-軌道耦合作用下的二維兩分量旋轉BEC體系,系統基態和動力學性質可由以下耦合的非線性方程組描述[35,50,51]:

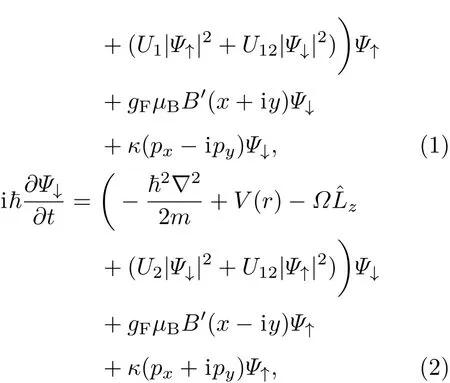
其中Ψj(j= ↑,↓)描述凝聚體的原子分布在自旋向上態和向下態的宏觀波函數,波函數滿足條件N是體系內總粒子數;動能項中～為普朗克常量;m為選取87Rb原子的質量;二維光束縛勢其中ω是束縛頻率;旋轉項中?代表旋轉頻率,其中規定?>0的正向旋轉為逆時針旋轉;?Lz=?i～(x?y?y?x)是沿著z方向的軌道角動量;原子相同自旋態之間相互作用參量為原子不同自旋態間相互作用參量為

其中a11和a22是相同自旋態間的S波散射長度,a12是不同自旋態間的S波散射長度;梯度磁場項中[52?54],其中B′代表磁場梯度強度的大小,朗德因子gF=?1/2,μB為玻爾磁矩;考慮Rashba類型自旋-軌道耦合,κ表示自旋-軌道耦合強度的大小,px和py分別描述在x和y方向的動量算符.進一步可以得到無量綱化的耦合方程組[35,50,51]:

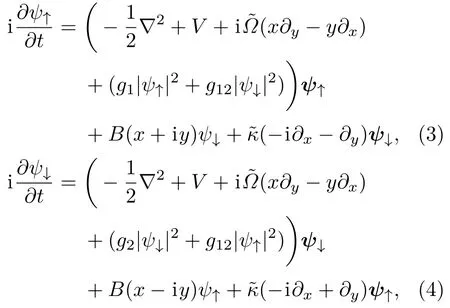
無量綱化波函數ψj=N?1/2ahΨj(j= ↑,↓),并且滿足歸一化條件無量綱化光束縛勢無量綱化相互作用強度分別為g1=4πa11N,g2=4πa22N 和g12=4πa12N;散射長度選為a11=a22=100.40aB和a12=33.4aB,aB是玻爾半徑;無量綱化的旋轉頻率,自旋-軌道耦合強度和磁場梯度強度分別為??,?κ和B;諧振勢的特征長度為在數值計算時,分別選用和ω～/(gFμBah)作為長度,時間,能量,自旋-軌道耦合強度和磁場梯度強度的單位.通過虛時演化方法求解(3)和(4)式得到基態[55?58],空間離散采用二階中心有限差分,時間迭代采用線性項隱式和非線性項顯式.數值計算網格為300×300,對應計算體系為12×12(a2h),初始試探函數為復數值的隨機數.

3 研究結果與討論

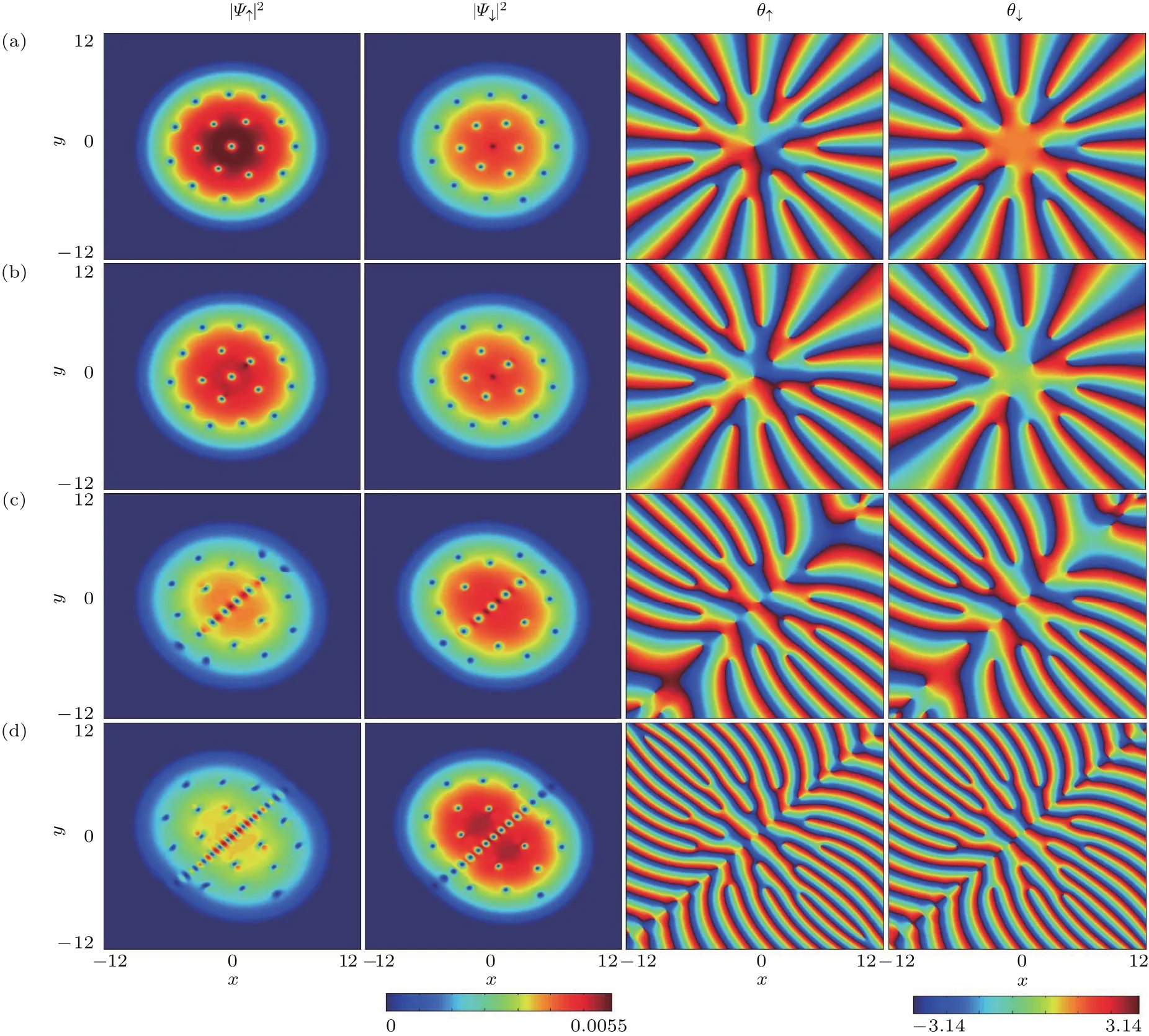
圖1 不同自旋-軌道耦合強度下梯度磁場中兩分量87Rb BEC基態粒子數密度分布(第1,2列)和相位分布(第3,4列)(a)?κ=0;(b)?κ=0.2;(c)?κ=0.8;(d)?κ=2;其余模擬參數選為g1=g2=6000,g12=2000,B=0.6,??=0.4和ω=2π×250 HzFig.1.Particle number densities(the fi rst and second columns)and phase distributions(the third and fourth columns)of ground state of the two-component BEC of 87Rb for the diff erent spin-orbit coupling strengths.The parameters are set as follows:(a)?κ=0;(b)?κ=0.2;(c)?κ=0.8;(d)?κ=2;and the rest of parameters are g1=g2=6000,g12=2000,B=0.6,??=0.4 andω=2π×250 Hz.

首先討論自旋-軌道耦合對體系基態的影響.固定磁場梯度強度和旋轉頻率,利用虛時演化方法數值模擬得到不同自旋-軌道耦合強度下對應的基態結構.基態粒子數密度和相位分布如圖1所示.第1,2列分別為自旋向上和自旋向下分量的密度分布,第3,4列分別為對應的相位分布.相位圖中可以看到有許多相位割線,從割線藍色一側到紅色一側相位存在從?π到π的不連續跳躍.割線端點對應粒子數密度分布,圖中密度極小值點即為渦旋核.當體系沒有自旋-軌道耦合時,由于有旋轉勢存在,凝聚體各個自旋組分都會出現渦旋,如圖1(a)所示.此外,由于產生渦旋的數目與旋轉頻率成正比,因此體系會出現一定數量的渦旋并以三角渦旋格子形式存在.其中每一個渦旋在自旋構型中實際上都對應一個skyrmion,因此也稱此時的基態結構為skyrmion格子,下文將詳細討論.引入較小的自旋-軌道耦合強度?κ=0.2,如圖1(b)所示,三角渦旋格子排列規則稍微被打破,有一些渦旋開始偏離原來位置.進一步將自旋-軌道耦合增強到?κ=0.8,發現凝聚體對角線方向出現整齊排列的渦旋列,尤其是處于中心對角線上的渦旋排列更緊密.同理,因為每個渦旋對應自旋構型上每個skyrmion,這樣的渦旋列也被稱為自旋空間下的skyrmion列,如圖1(c)所示.從相位圖中也可以看出,相位的奇異點表現為列狀分布.在較強自旋-軌道耦合?κ=2作用下,凝聚體基態依然保持為skyrmion列,而且排列分布更整齊,如圖1(d)所示.因此,在梯度磁場中,改變自旋-軌道耦合強度,體系實現了從skyrmion格子到skyrmion列的轉化.從物理角度也不難理解這樣的現象:一方面,原子自旋和質心運動的耦合,會導致原子的自旋結構發生改變;另一方面,自旋-軌道耦合和梯度磁場共同作用,會改變體系內渦旋分布的對稱性,使得渦旋排布從格子狀轉變為列狀.與前人的研究結果相比,在沒有梯度磁場的各向同性自旋-軌道耦合旋轉BEC中,增加自旋-軌道耦合強度,體系基態僅僅支持skyrmion格子[35].

接下來,固定弱的自旋-軌道耦合強度,研究在不同旋轉頻率下梯度磁場對基態結構的影響.首先考慮旋轉慢的情況,開始體系沒有感受到梯度磁場,基態表現為平面波相,如圖2(a1)所示.類似于無旋轉自旋-軌道耦合兩分量BEC中的結果,當組分內相互作用大于組分間相互作用,體系基態為平面波相[27].盡管此時有旋轉,但是一方面旋轉頻率太小不足以產生渦旋,另一方面旋轉勢的作用小于規范勢對體系的作用,所以只有平面波相出現.一旦體系考慮了梯度磁場,基態結構將發生變化.由于梯度磁場中心處為磁場零點,對應拓撲缺陷的奇異點,因此該磁場零點進入凝聚體中,便會引入產生一個拓撲缺陷,該缺陷對應自旋向上分量的粒子數密度分布中一個渦旋.從兩個分量整體分析,一個分量表現為渦旋,另一個分量表現為孤子,這樣的結構在文獻中被稱為半渦旋[55],如圖2(a2)所示.實際上它對應自旋空間的一個half-skyrmion,下文將詳細討論.因此,當自旋-軌道耦合和旋轉頻率都小時,梯度磁場的引入實現了體系從平面波相到half-skyrmion的轉變.進一步考慮旋轉快的情況,沒有外磁場時,體系出現大量渦旋,并圍繞圓心以徑向排列形成渦旋格子,如圖2(b1)所示.當增大磁場梯度強度時,原來徑向排列的渦旋格子結構被打破,中心處密度開始耗散,形成了橢圓狀的環形結構.環形區域上的渦旋形成三角格子,環形內部及勢阱中心區域形成巨渦旋,主對角線區域凝聚體粒子數較多,次對角線區域的凝聚體粒子數較少,如圖2(b2)所示.這是因為強磁場梯度導致強的磁力,凝聚體原子很難聚在中心處,所以原子云從中心處擴散,形成不均勻的密度分布.此外,由于有旋轉的存在,所以磁力和旋轉兩種作用相互競爭,出現了中心處的巨渦旋結構.

進一步,固定強自旋-軌道耦合,探索在不同旋轉頻率下梯度磁場對基態的影響.同樣先考慮旋轉慢的情況,當磁場梯度為零,強自旋-軌道耦合誘導兩條互相垂直的渦旋列,如圖3(a1)所示.在相位圖中,被渦旋列分隔開的4個區域表現為平面波分布,而且相位值由小變大的方向為逆時針方向,正如黑色箭頭所示.如果磁場梯度強度增強,發現體系結構僅僅表現為單列渦旋態,沿著傾斜方向排布,如圖3(a2)所示.相位圖中箭頭表示平面波位相值的變化趨勢.物理上不難解釋,渦旋總是對應著自旋的劇烈翻轉和起伏,這使得自旋偏離面內.而梯度磁場對原子的磁矩會產生作用,如果原來非面內的磁矩發生翻轉,使得原子自旋沿著梯度磁場的方向,磁場對渦旋產生起一定的抑制作用,當磁場梯度變強時,抑制作用占主導地位,因此體系內渦旋數目變少.這種情況下,通過調節磁場梯度實現了兩條互相垂直的渦旋列向單條渦旋列的轉變.然后考慮旋轉快的情況,在無磁場時,強自旋-軌道耦合和強旋轉頻率能夠導致伴隨巨渦旋的渦旋格子態,此結果也與前人的工作符合[34],如圖3(b1)所示.當梯度磁場增大,發現凝聚態被擠壓到主對角位置,這是由于強磁力所引起的.值得注意的是,體系內出現hidden渦旋[59],如圖3(b2)所示.hidden渦旋是一種很有趣的拓撲缺陷,此類渦旋在密度分布中無法找到渦旋核,只能從相位圖中觀察到其相位奇異點.而且如同可見渦旋,自身能夠攜帶角動量[59].圖3(b2)中的hidden渦旋分布于體系次對角線區域,從相位圖中可以清晰地看到,橢圓線圈之內的渦旋就是hidden渦旋.之前關于hidden渦旋的研究幾乎都是基于單分量旋轉BEC體系[59,60],這里提供了一種在兩分量BEC中產生hidden渦旋的方法,為將來在高自旋BEC體系、超流和超導領域實現hidden渦旋提供了理論和實驗指導.

最后討論了不同基態的自旋結構,定義自旋平均值為[35,55]:

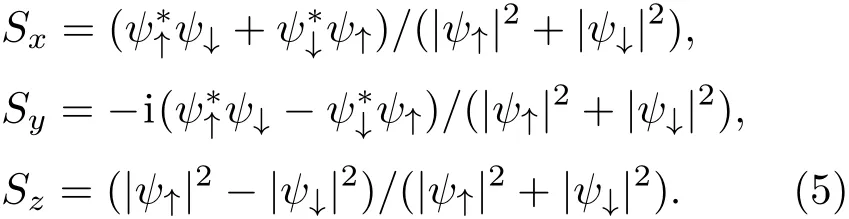
也給出了計算拓撲荷公式

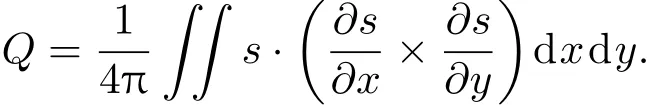
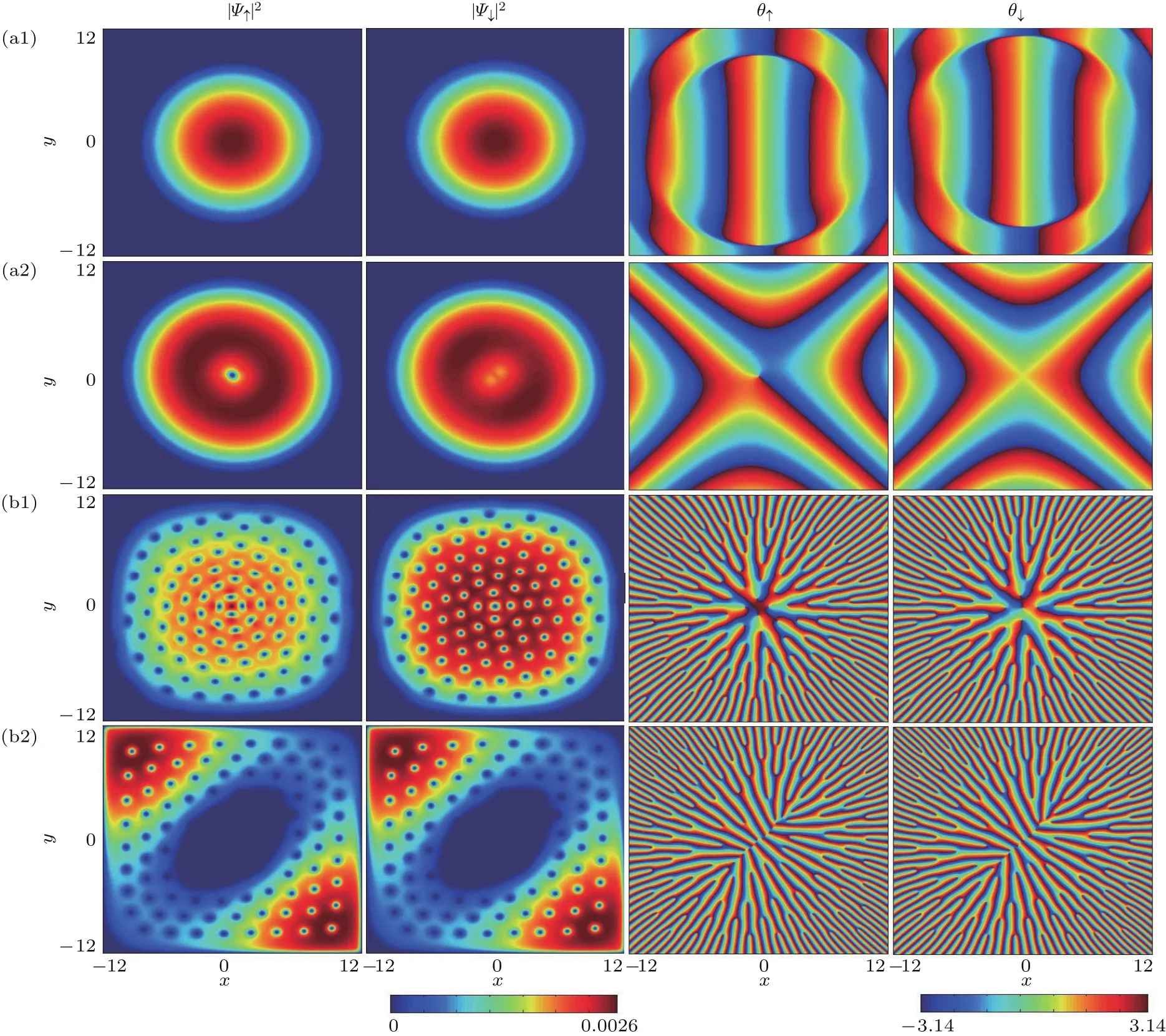
圖2 在弱自旋-軌道耦合下,不同磁場梯度強度對基態的影響.第1,2列描述兩分量87Rb凝聚體基態的粒子數密度分布;第3,4列表示對應的相位分布(a1)B=0,??=0.1;(a2)B=3.8,??=0.1;(b1)B=0,??=0.9;(b2)B=3.8,??=0.9;其余模擬參數選為g1=g2=6000,g12=2000,?κ=0.8和ω=2π×250 HzFig.2.Eff ects of the diff erent magnetic fi eld gradient strength on ground state when the spin-orbit coupling is weak.The fi rst and second columns are the particle number densities of the two-component BEC of 87Rb;the third and fourth columns are the corresponding phase distributions.The parameters are set as follows:(a1)B=0,??=0.1;(a2)B=3.8,??=0.1;(b1)B=0,??=0.9;(b2)B=3.8,??=0.9;and the other parameters are g1=g2=6000,g12=2000,?κ=0.8 and ω =2π×250 Hz.

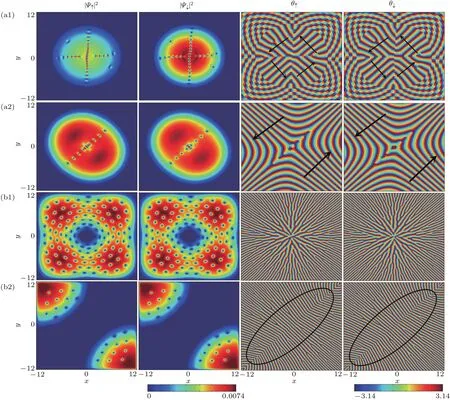
圖3 在強自旋-軌道耦合下,不同磁場梯度強度對基態的影響.第1,2列描述兩分量87Rb凝聚體基態的粒子數密度分布;第3,4列表示對應的相位分布(a1)B=0,??=0.1;(a2)B=3.8,??=0.1;(b1)B=0,??=0.9;(b2)B=3.8,??=0.9;其余模擬參數選為g1=g2=6000,g12=2000,?κ=4和ω=2π×250 HzFig.3.Eff ects of the diff erent magnetic fi eld gradient strength on ground state when the spin-orbit coupling is strong.The fi rst and second columns are the particle number densities of the two-component BEC of 87 Rb;the third and fourth columns are the corresponding phase distributions:(a1)B=0,??=0.1;(a2)B=3.8,??=0.1;(b1)B=0,??=0.9;(b2)B=3.8,??=0.9(the other parameters are g1=g2=6000,g12=2000,?κ=4 andω=2π×250 Hz).

其中積分核為拓撲荷密度.圖4(a)是對應于圖1(a)的自旋結構,此時自旋-軌道耦合強度為零,體系中skyrmion形成三角格子排列,計算每個skyrmion對應的拓撲荷為1,屬于整數skyrmion.通過分析體系內每個skyrmion的自旋結構,發現skyrmion自旋包括兩種繞向及順時針方向和逆時針方向.圖4(a)圓圈中skyrmion的自旋結構是逆時針繞向,其對應的局部放大結構如圖4(f)所示.值得注意的是,中心處表現為一個雙曲型meron結構[51],這是由于梯度磁場所引起的.圖4(b)是對應于圖1(c)的自旋結構,當自旋-軌道耦合強度增大,原來的skyrmion格子轉變為skyrmion列,沿著次對角方向排列.與此同時,關于次對角線對稱的兩個區域,面內自旋方向是相反的.此外,也發現體系內所有skyrmion自旋繞向都為順時針方向,為了更清晰地看到自旋排布,給出了圖4(b)三角形中skyrmion的局部放大結構,如圖4(c)所示.圖4(d)是對應于圖2(a2)的自旋結構,自旋在面內呈現雙曲四極分布,靠近中心處自旋發生翻轉.計算拓撲荷為0.5,這樣的自旋結構被稱為half-skyrmion.圖4(e)是對應于圖3(a2)的自旋結構,當在強自旋-軌道耦合和慢的旋轉情況下,梯度磁場的增強會導致體系內僅僅出現單條skyrmion列,而且沿著次對角線方向分布.此時體系內所有的skyrmion的自旋繞向為順時針方向.

將來工作可以考慮具有其他形式的自旋-軌道耦合體系,例如Rashba-Dresselhaus自旋-軌道耦合 BEC,SU(3)自旋-軌道耦合 BEC和Weyl型自旋-軌道耦合BEC[61?63]等,此時基態結構將展現出更多有趣的特性.進一步,將考慮具有偶極相互作用和高自旋的BEC系統[64,65],由于長程各向異性的作用力和自旋交換相互作用,會對凝聚體的基態相貌、穩定性以及實時動力學性質產生顯著影響,可以誘導更豐富的量子態和自旋紋理.

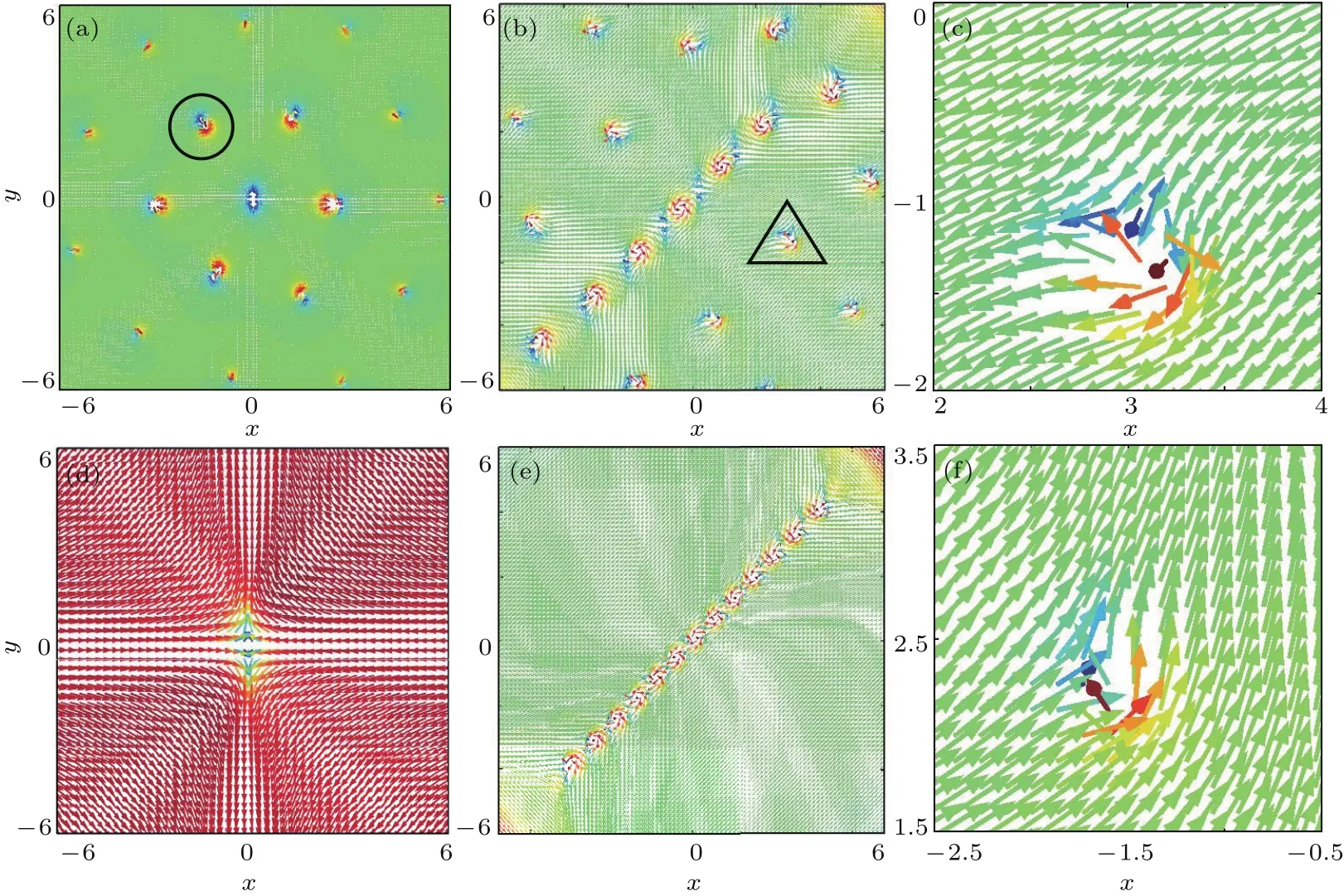
圖4 基態的自旋結構 (a)對應圖1(a)的自旋結構;(b)對應圖1(c)的自旋結構;(c)描述圖4(b)中三角區域自旋的局部放大結構;(d)對應圖2(a2)的自旋結構;(e)對應圖3(a2)的自旋結構;(f)描述圖4(a)中圓形區域自旋的局部放大結構(自旋密度值變化區間為從?1(藍色)到1(紅色))Fig.4.The spin texture of the ground state:(a)Spin texture corresponding to the Fig.1(a);(b)spin texture corresponding to the Fig.1(c);(c)local enlargement of the spin in the triangular region in Fig.4(b);(d)spin texture corresponding to the Fig.2(a2);(e)spin texture corresponding to the Fig.3(a2);(f)local enlargement of the spin in the circular region in Fig.4(a)(Values of the pseudospin density are from?1(blue)to 1(red)).

4 結 論

本文利用準二維Gross-Pitaevskii方程,研究了自旋-軌道耦合和梯度磁場對旋轉兩分量BEC基態的影響,得到了不同參數下的基態結構.結果表明:自旋-軌道耦合與梯度磁場共同作用,能夠導致體系基態由skyrmion格子轉變為skyrmion列;當自旋-軌道耦合強度和旋轉頻率都小,磁場梯度強度的增大能夠引起基態從平面波相到halfskyrmion的轉化;對于自旋-軌道耦合強度和旋轉頻率都大的情況,梯度磁場可誘導體系產生hidden渦旋.最后,還討論了基態的自旋結構.在自旋-軌道耦合BEC中,梯度磁場不僅僅對于研究奇異量子相提供了一個新的機遇,而且對于控制不同基態相間的轉化發揮了關鍵作用.這些有趣的結果可為BEC中的相關拓撲激發實驗提供指導.

[1]Hall D S,Matthews M R,Ensher J R,Wieman C E,Cornell E A 1998 Phys.Rev.Lett.81 1539

[2]Matthews M R,Anderson B P,Haljan P C,Hall D S,Wieman C E,Cornell E A 1999 Phys.Rev.Lett.83 2498

[3]Anderson B P,Haljan P C,Regal C A,Feder D L,Collins L A,Clark C W,Cornell E A 2001 Phys.Rev.Lett.86 2926

[4]Kasamatsu K,Tsubota M 2004 Phys.Rev.Lett.93 100402

[5]Qu C L,Pitaevskii L P,Stringari S 2016 Phys.Rev.Lett.116 160402

[6]Williams J E,Holland M J 1999 Nature 401 568

[7]?hberg P,Santos L 2001 Phys.Rev.Lett.86 2918

[8]Kasamatsu K,Tsubota M,Ueda M 2004 Phys.Rev.Lett.93 250406

[9]Schweikhard V,Coddington I,Engels P,Tung S,Cornell E A 2004 Phys.Rev.Lett.93 210403

[10]Cipriani M,Nitta M 2013 Phys.Rev.Lett.111 170401

[11]Kasamatsu K,Tsubota M,Ueda M 2003 Phys.Rev.Lett.91 150406

[12]Battye R A,Cooper N R,Sutcliff e P M 2002 Phys.Rev.Lett.88 080401

[13]Martikainen J P,Collin A,Suominen K A 2002 Phys.Rev.Lett.88 090404

[14]Lin Y J,García K J,Spielman I B 2011 Nature 471 83

[15]Ji S C,Zhang J Y,Zhang L,Du Z D,Zheng W,Deng Y J,Zhai H,Chen S,Pan J W 2014 Nature Phys.10 314

[16]Wu Z,Zhang L,Sun W,Xu X T,Wang B Z,Ji S C,Deng Y J,Chen S,Liu X J,Pan J W 2016 Science 354 83

[17]Huang L H,Meng Z M,Wang P J,Peng P,Zhang S L,Chen L C,Li D H,Zhou Q,Zhang J 2016 Nature Phys.12 540

[18]Ruseckas J,Juzeliúnas G, ?hberg P,Fleischhauer M 2005 Phys.Rev.Lett.95 010404

[19]Campbell D L,Juzeliúnas G,Spielman I B 2011 Phys.Rev.A 84 025602

[20]Zhang J Y,Ji S C,Chen Z,Zhang L,Du Z D,Yan B,Pan G S,Zhao B,Deng Y J,Zhai H,Chen S,Pan J W 2012 Phys.Rev.Lett.109 115301

[21]Liu X J,Borunda M F,Liu X,Sinova J 2009 Phys.Rev.Lett.102 046402

[22]Anderson B M,Spielman I B,Juzeliúnas G 2013 Phys.Rev.Lett.111 125301

[23]Anderson B M,Juzeliúnas G,Galitski V M,Spielman I B 2012 Phys.Rev.Lett.108 235301

[24]Cheuk L M,Sommer A T,Hadzibabic Z,Yefsah T,Bakr W S,Zwierlein1 M W 2012 Phys.Rev.Lett.109 095302

[25]Wang P J,Yu Z Q,Fu Z K,Miao J,Huang L H,Chai S J,Zhai H,Zhang J 2012 Phys.Rev.Lett.109 095301

[26]Lan Z H,?hberg P 2014 Phys.Rev.A 89 023630

[27]Wang C J,Gao C,Jian C M,Zhai H 2010 Phys.Rev.Lett.105 160403

[28]Sinha S,Nath R,Santos L 2011 Phys.Rev.Lett.107 270401

[29]Hu H,Ramachandhran B,Pu H,Liu X J 2012 Phys.Rev.Lett.108 010402

[30]Yu Z Q 2013 Phys.Rev.A 87 051606

[31]Bhat I A,Mithun T,Malomed B A,Porsezian K 2015 Phys.Rev.A 92 063606

[32]Li Y,Zhou X F,Wu C J 2016 Phys.Rev.A 93 033628

[33]Kato M,Zhang X F,Saito H 2017 Phys.Rev.A 95 043605

[34]Xu X Q,Han J H 2011 Phys.Rev.Lett.107 200401

[35]Liu C F,Fan H,Zhang Y C,Wang D S,Liu W M 2012 Phys.Rev.A 86 053616

[36]Zhou X F,Zhou J,Wu C J 2011 Phys.Rev.A 84 063624

[37]Sakaguchi H,Umeda K 2016 J.Phys.Soc.Jpn.85 064402

[38]Zhang X F,Gao R S,Wang X,Dong R F,Liu T,Zhang S G 2013 Phys.Lett.A 377 1109

[39]Wang X,Tan R B,Du Z J,Zhao W Y,Zhang X F,Zhang S G 2014 Chin.Phys.B 23 070308

[40]Wang H,Wen L H,Yang H,Shi C X,Li J H 2017 J.Phys.B:At.Mol.Opt.Phys.50 155301

[41]Radi?J,Sedrakyan T A,Spielman I B,Galitski V 2011 Phys.Rev.A 84 063604

[42]Fetter A L 2014 Phys.Rev.A 89 023629

[43]Chen G P 2015 Acta Phys.Sin.64 030302(in Chinese)[陳光平 2015物理學報64 030302]

[44]Liu C F,Liu W M 2012 Phys.Rev.A 86 033602

[45]Kennedy C J,Siviloglou G A,Miyake H,Burton W C,Ketterle W 2013 Phys.Rev.Lett.111 225301

[46]Ray M W,Ruokokoski E,Kandel S,M?tt?nen M,Hall D S 2014 Nature 505 657

[47]Ray M W,Ruokokoski E,Tiurev K,M?tt?nen M,Hall D S 2015 Science 348 544

[48]Hall D S,Ray M W,Tiurev K,Ruokokoski E,Gheorghe A H,M?tt?nen M 2016 Nature Phys.12 478

[49]Kawaguchi Y,Nitta M,Ueda M 2008 Phys.Rev.Lett.100 180403

[50]Li J,Yu Y M,Zhuang L,Liu W M 2017 Phys.Rev.A 95 043633

[51]Liu J S,Li J,Liu W M 2017 Acta Phys.Sin.66 130305(in Chinese)[劉靜思,李吉,劉伍明 2017物理學報 66 130305]

[52]Leanhardt A E,G?rlitz A,Chikkatur A P,Kielpinski D,Shin Y,Pritchard D E,Ketterle W 2002 Phys.Rev.Lett.89 190403

[53]Pritchard D E 1983 Phys.Rev.Lett.51 1336

[54]Leanhardt A E,Shin Y,Kielpinski D,Pritchard D E,Ketterle W 2003 Phys.Rev.Lett.90 140403

[55]Han W,Zhang S Y,Jin J J,Liu W M 2012 Phys.Rev.A 85 043626

[56]Dalfovo F,Stringari S 1996 Phys.Rev.A 53 2477

[57]Zhang X F,Dong R F,Liu T,Liu W M,Zhang SG 2012 Phys.Rev.A 86 063628

[58]Bao W Z,Du Q 2004 SIAM J.Sci.Comput.25 1674

[59]Wen L H,Xiong H W,Wu B 2010 Phys.Rev.A 82 053627

[60]Mithun T,Porsezian K,Dey B 2014 Phys.Rev.A 89 053625

[61]Ruokokoski E,Huhtam?ki J A M,M?tt?nen M 2012 Phys.Rev.A 86 051607

[62]Barnett R,Boyd G R,Galitski V 2012 Phys.Rev.Lett.109 235308

[63]Chen G J,Chen L,Zhang Y B 2016 New J.Phys.18 063010

[64]Zhang X F,Zhang P,Chen G P,Dong B,Tan R B,Zhang S G 2015 Acta Phys.Sin.64 060302(in Chinese)[張曉斐,張培,陳光平,董彪,譚仁兵,張首剛 2015物理學報64 060302]

[65]Liu C F,Wan W J,Zhang G Y 2013 Acta Phys.Sin.62 200306(in Chinese)[劉超飛,萬文娟,張贛源2013物理學報62 200306]