任意復包絡信號的勻速運動目標回波脈間補償及相干積累?
馮西安 張楊梅2)?
1)(西北工業大學航海學院,西安 710072)
2)(西安航空學院電子工程學院,西安 710077)
(2017年10月11日收到;2018年3月7日收到修改稿)
1 引 言
微弱信號檢測可使用多脈沖積累.North[1]曾指出:從理論上講,信號積累是一種最有效的微弱目標檢測方式.但實際中,信號積累檢測仍存在一定的難度,尤其是運動目標的積累檢測.迄今為止,國內外的專家和學者們針對低可觀測性運動目標的長時間相干積累問題展開了廣泛研究,并取得了豐碩的成果.
長時間相干積累主要包括精確匹配濾波、運動補償及Fourier變換(FFT)積累3個重要環節,其中的關鍵問題是運動補償,將回波包絡對齊.目前,常用的運動補償方法有最大相關法[2]、最小熵法[3,4]、Hough變換[5?7]、Radon-Fourier變換[8?11]、Keystone變換[12?16]等.這些積累方法多使用脈壓性能好、多普勒容限大的線性調頻(LFM)信號進行建模、公式推導,得出相應結論.然而,在現代聲吶、水下制導領域,除了LFM信號以外,人們還使用復雜多樣的波形形式來滿足不同的應用目的和環境需求.當考慮波形穩健傳輸、精準測速時,多選擇較簡單的連續波(CW)信號;考慮低截獲主動隱蔽探測時,則使用復雜的大時間帶寬積編碼信號[17];現代波形設計還使用最優化算法和計算機迭代程序生成發射序列用于抗干擾、信道匹配、目標識別等目的[18].隨著復雜波形在實際探測系統中的廣泛應用,在長時間信號積累中,任意信號波形的運動目標回波補償及相干積累是需要研究解決的問題.
本文針對水聲探測系統使用的信號形式種類繁多這種實際情況,研究給出了任意復包絡信號的勻速運動目標回波脈間補償及相干積累檢測方法,并進行了必要的仿真和水池實驗驗證.
2 信號積累中的多脈沖回波模型
將水聲探測系統的發射信號表示為復包絡和載波形式uc(t)exp(j2πf0t),則當目標勻速運動時,使用脈內快時間tk和脈間慢時間tm表示的多脈沖回波為
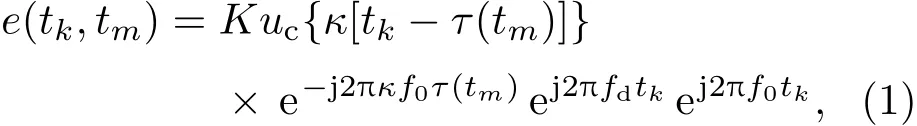
式中κ=(c?v0)/(c+v0)是展縮系數,c是聲速,v0是目標速度;K是反射系數;τ表示回波時延,τ(tm)=2R(tm)/(c?v0)是第m個回波的時延,其中R(tm)=R0+v0tm,R0是第一個回波對應的目標距離.慢時間tm=(m?1)Tr,Tr為脈沖重復周期(pulse repetition time,PRT),其倒數為脈沖重復頻率fr(pulse repetition frequency,PRF).fd=(κ?1)f0是多普勒頻率.降頻處理后,得到多脈沖回波復包絡為
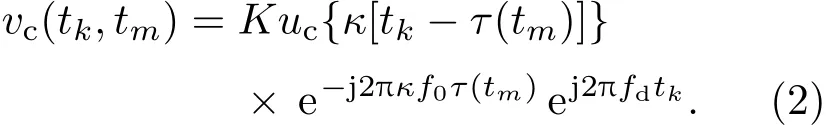
vc(tk,tm)是二維函數,一維是距離維,另一維是脈沖維.回波復包絡的頻譜為
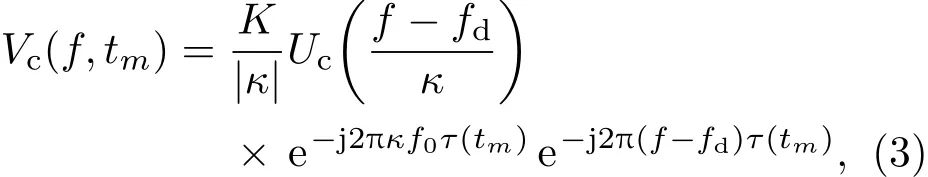
式中Uc(f)是復包絡uc(t)的頻譜.將τ(tm)代入(2)式,整理后得
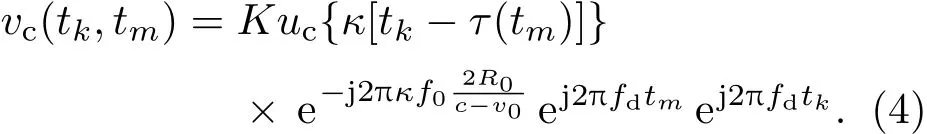
可見回波復包絡除了是發射信號復包絡的時延及壓縮形式以外,還增加了3個指數項:第一個是固定相位項;第二個是脈間慢時間多普勒頻移項;第三個是脈內快時間多普勒頻移項.從距離維看,目標運動使得回波包絡不能對齊,出現距離走動.長時間積累或運動速度較高時,還會出現跨距離單元走動.對于距離走動,需要進行運動補償將包絡對齊.從脈沖維看,脈沖幅度按照多普勒頻率的復正弦規律變化,因此,脈沖維也叫多普勒維.相干積累時需要在脈沖維做FFT以補償脈間慢時間多普勒頻移項.
3 脈沖壓縮信號的廣義模糊函數表示
對回波復包絡進行精確匹配濾波,即讓匹配濾波器的脈沖響應取為
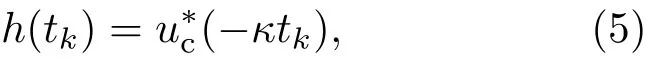
或者在頻域將其傳輸函數取為
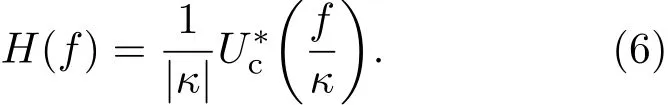
則在時域,匹配濾波器輸出的脈壓信號可一般地表示為
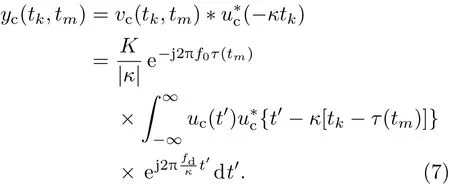
可以看到,對于不同形式的發射波形,將其復包絡代入該式的積分,得到的yc(tk,tm)形式不盡相同.另外,這個表示式沒有給出脈壓信號的距離走動和多普勒維的脈沖幅度變化信息.這些信息隱藏在積分式中,給距離走動分析、運動補償及多普勒維的相干積累帶來困難.以往的文獻采用LFM信號的壓縮形式來分析這些問題,得出的結論不具有一般性.本文通過構建一種時延τ和展縮系數κ的函數來表示脈壓信號,使得任意復包絡信號的脈壓波形不僅能夠用統一的數學模型來表述,而且提供了多脈沖回波的距離走動信息和多普勒頻移信息.對于發射信號s(t),所構造的函數為
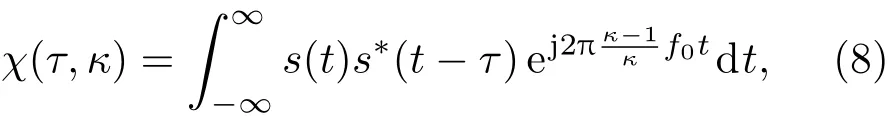
它與窄帶模糊函數相似,被稱為廣義模糊函數(generalized ambiguity function,GAF).特別地,κ=1即目標靜止時,GAF退化為自相關函數.
GAF是信號的脈沖壓縮形式,具有顯著的主瓣和較低的旁瓣,主瓣峰值位于時延τ=0、壓縮κ=1處,峰值位置與波形形式無關.
利用fd=(κ?1)f0,(7)式中的積分可表示為
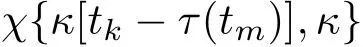
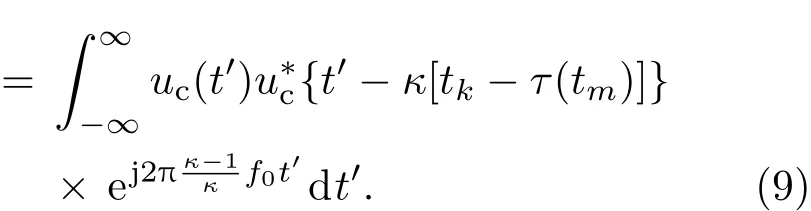
它是GAF的壓縮和延時,表示了回波復包絡的壓縮形式.將其代入(7)式,可得
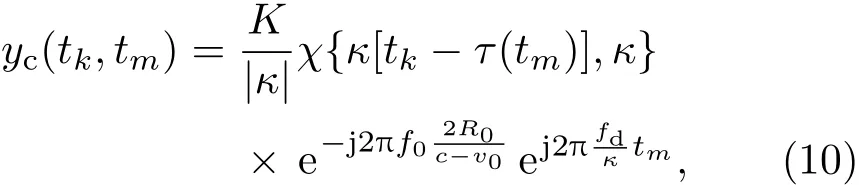
該式是任意復包絡信號回波的脈壓信號模型.不難看出,χ{κ[tk?τ(tm)],κ}具有窄的主瓣,其峰值位置τ(tm)給出了脈壓信號的距離走動.同時,相位項exp(j2πfd/κtm)給出了脈沖維的多普勒信息.
本文作者在文獻[19]中采用所構建的GAF給出了CW信號、LFM信號、m序列編碼信號、Costas跳頻編碼信號的基帶脈壓信號具體表達式,其中對LFM信號推導得到的脈壓信號表示形式與文獻[12,13,15]中由回波復包絡精確匹配得到的結果完全相同.
4 脈壓信號的距離走動及運動補償
4.1 脈壓信號的距離走動
(4)式和(10)式從時域上清楚表明了距離走動的現象.運動產生距離走動,在每次發射探測脈沖時,目標距離不同,回波復包絡的時延發生了變化.回波復包絡經距離向脈壓后,匹配濾波器輸出的脈壓信號峰值位置也各不相同.
距離走動的本質需要在頻域進行分析.為此,給出(10)式的頻域形式.由(3)式和(6)式可得脈壓信號的距離頻域表示式為
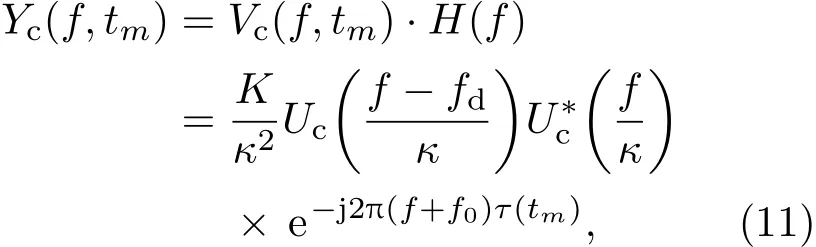
式中指數項表明,距離頻率f與脈間慢時間tm之間存在耦合.當轉換到時域時,這種耦合將直接導致(10)式中各壓縮脈沖的峰值位置彼此不同,出現距離走動.所以,從頻域上看,距離頻率與脈間慢時間之間的耦合是導致脈壓信號距離走動的根本原因.
校正距離走動就是解除f與tm間的耦合.使用Keystone變換對脈間慢時間tm做變量代換就可消除頻率與時間耦合,使得距離頻率不再受脈間慢時間的影響.但是注意到(10)式,匹配濾波器輸出存在一個exp[j2πfd/(κtm)]項,它是tm的復正弦函數,頻率是多普勒頻率.因此,經Keystone變換后,變換到時域的脈壓信號還需要對脈沖維做FFT,將多普勒頻移進行補償,得到相干積累的結果.相干積累的峰值位置對應目標距離和多普勒頻率.
4.2 運動目標回波補償
Keystone變換最初是應用于SAR/ISAR(synthetic aperture radar/inverse synthetic aperture radar)成像中的一種距離走動校正技術,它利用時間尺度變換消除目標速度與距離頻域之間的耦合,從而實現運動目標的跨距離單元走動校正.將Keystone變換用于勻速運動目標長時間相干積累,可消除脈壓信號中的距離頻率f與脈間慢時間tm的耦合,實現距離走動校正.
Keystone變換定義為
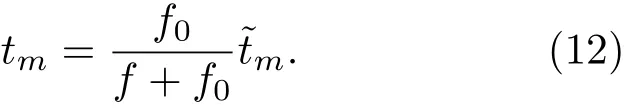
這個線性尺度變換將f-tm平面上的矩形支撐域變為f-?tm平面上一個倒梯形或楔石形,因此命名Keystone變換.若tm是脈間慢時間,那么Keystone變換就是對脈間慢時間進行的尺度變換,將tm變換為?tm.通過這種尺度變換改變脈沖位置,校正運動引起的線性距離走動.
將(12)式代入脈壓信號的頻域表示式(11)式,整理后可得對齊峰值位置后的脈壓信號頻域表達式為
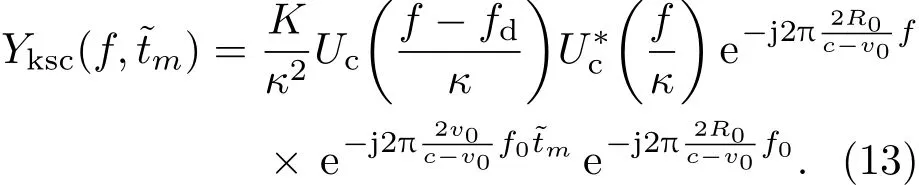
可見Keystone變換解除了f與?tm間的耦合,消除了脈間慢時間對距離頻率的影響.將(13)式變換到時域,整理后得其時域表達式
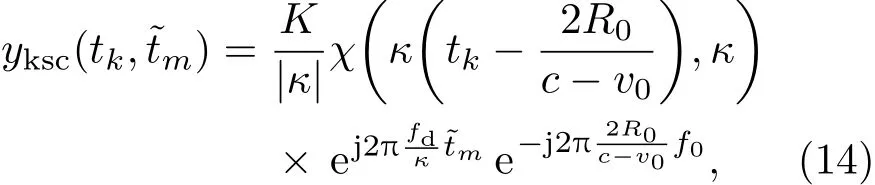
式中χ的峰值位置只與初始時刻的目標位置R0有關,而與tm無關.這表明Keystone變換將運動引起的回波跨距離單元走動校正到同一距離單元,使回波復包絡的壓縮形式對齊.再注意到,(14)式中的第一個指數項是?tm的正弦函數,它使得脈壓信號的相位不同,采用FFT進行該項補償,可得到相干積累的結果.
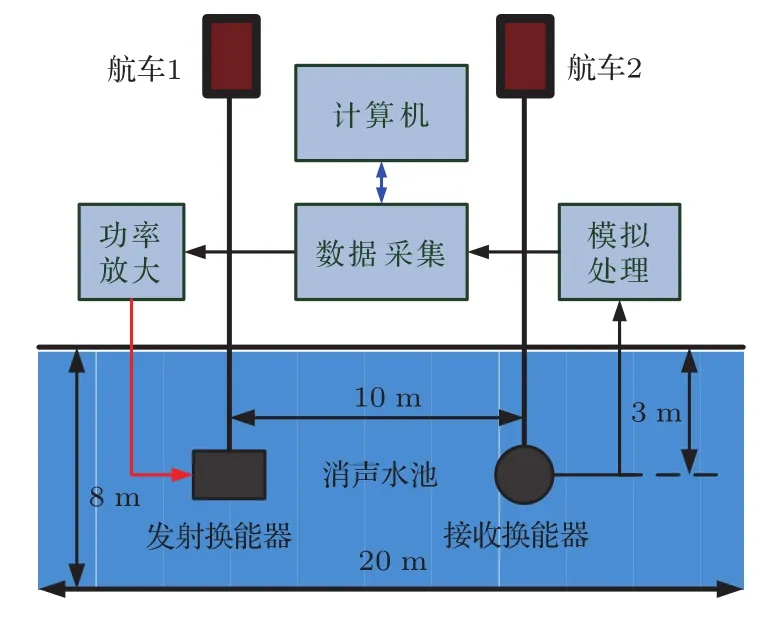
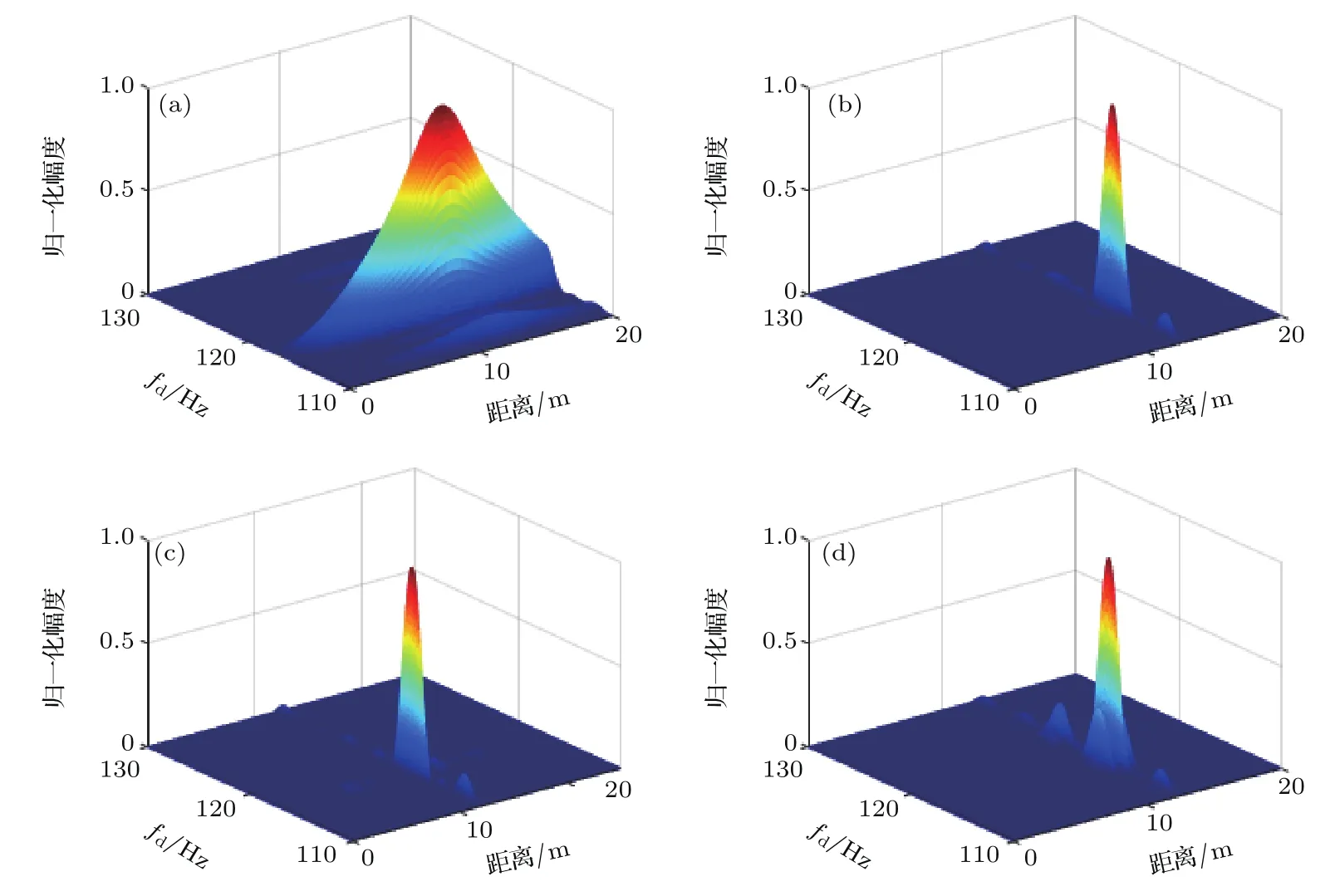
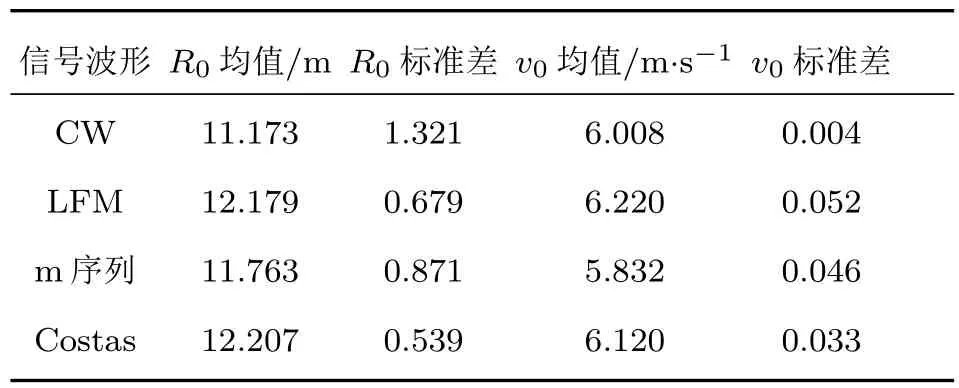
另外,(14)式中的第一個指數項是對頻率為fd/κ的正弦信號在脈沖維采樣,采樣頻率即脈沖重復頻率fr,數字譜分析范圍為(?fr/2,fr/2).當fr>fd時,頻率fd/κ落在譜分析范圍內,可從頻譜上觀測到.但是,當目標速度較快,多普勒頻率較高,而脈沖重復頻率較低,即fr 式中fd0是頻譜上觀察到的模糊多普勒頻率,nk是模糊數. 將(15)式代入(14)式得 式中的第三個指數項為模糊項,必須加以補償.當速度已知時,根據模糊數估計nk,使用對模糊項進行補償,補償后多普勒模糊后的壓縮回波為 再對慢時間維做FFT,可得到考慮了多普勒模糊的相干積累結果為 式中M是脈沖個數,M Tr是脈沖維正弦信號的持續時間. 以上推導均假設目標速度v0已知.當目標速度未知時,則需要設計匹配濾波器組對回波包絡進行精確匹配濾波,并使用匹配濾波器組對應的多普勒頻率或速度估計模糊數nk,以便補償模糊項,但這會增加信號積累的計算量.當目標做勻加速運動時,加速度與慢時間將發生二次耦合,二次耦合將導致積累時間內目標回波的距離彎曲,距離彎曲需要使用二階廣義Keystone變換進行補償[20]. 信號積累過程的仿真實驗:設聲吶分別發射CW信號、LFM信號、m序列編碼信號和Costas跳頻編碼信號來探測目標;信號參數設置為中心頻率f0=15 kHz,帶寬B=10 kHz,采樣頻率fs=100 kHz,脈沖寬度T=30 ms,脈沖重復周期Tr=0.2 s,脈沖個數M=10;目標距離R0=75 m,速度v0=?30 kn(1 kn≈0.5117 m/s,目標向觀測點勻速運動),對應的多普勒頻率fd=310.2 Hz;信噪比SNR=5 d B,信噪比取值較高,以便能夠在時域上看到回波位置. 采用本文的方法對4種信號波形積累的過程及結果如圖1—圖4所示.其中圖1(a),圖2(a),圖3(a)和圖4(a)是噪聲中的10個回波;圖1(b),圖2(b),圖3(b)和圖4(b)是精確匹配濾波后的脈壓信號;圖1(c),圖2(c),圖3(c)和圖4(c)是用Keystone變換補償運動以后對齊了的脈壓信號;這12幅圖均對波形取了絕對值,并用最大值歸一化;圖1(d),圖2(d),圖3(d)和圖4(d)是補償距離走動、去除多普勒模糊后,沿慢時間維做FFT積累的結果,圖中用峰值進行了歸一化,其中補償的多普勒模糊數由多普勒頻率fd與脈沖重復頻率fr之比得到,為62個. 從圖1—圖4的(a),(b)圖可以看到,由于目標運動,各周期的回波、脈壓信號均有距離走動,脈沖距離位置不齊.目標勻速運動時,脈沖位置在距離-慢時間平面上是一條傾斜直線.從圖1—圖4的(c)圖可見,在利用Keystone變換對脈壓信號進行距離走動校正以后,脈壓信號對齊到同一距離位置,分布在一條與距離軸垂直的直線上.從圖1—圖4的(d)圖可以看出,沿慢時間維做FFT,在距離-多普勒平面上出現了相干積累的峰值,峰值位置對應著目標距離和多普勒頻率,分別約為75 m,310.2 Hz,與仿真設置的參數相符合.還可看到,CW信號的脈沖壓縮比小,脈壓信號及積累結果在時間或距離維較寬,其余三種信號脈沖壓縮能力強,脈壓信號及積累后的結果都是尖銳的峰值. 圖1 CW信號的積累結果 (a)距離走動的回波;(b)隨距離走動的脈壓信號;(c)運動補償的脈壓信號;(d)積累結果的三維圖Fig.1.Accumulating result of CW signal:(a)Echo signal of moving target;(b)pulse compressed signal moving along with distance;(c)pulse compressed signal after motion compensation;(d)three-dimensional graph of accumulating results. 圖2 LFM信號的積累結果 (a)距離走動的回波;(b)隨距離走動的脈壓信號;(c)運動補償的脈壓信號;(d)積累結果的三維圖Fig.2.Accumulating result of LFM signal:(a)Echo signal of moving target;(b)pulse compressed signal moving along with distance;(c)pulse compressed signal after motion compensation;(d)three-dimensional graph of accumulating results. 圖3 m序列編碼信號的積累結果 (a)距離走動的回波;(b)隨距離走動的脈壓信號;(c)運動補償的脈壓信號;(d)積累結果的三維圖Fig.3.Accumulating result of m sequence coded signal:(a)Echo signal of moving target;(b)pulse compressed signal moving along with distance;(c)pulse compressed signal after motion compensation;(d)three-dimensional graph of accumulating results. 圖4 Costas跳頻編碼信號的積累結果 (a)距離走動的回波;(b)隨距離走動的脈壓信號;(c)運動補償的脈壓信號;(d)積累結果的三維圖Fig.4.Accumulating result of Costas frequency hop coded signal:(a)Echo signal of moving target;(b)pulse compressed signal moving along with distance;(c)pulse compressed signal after motion compensation;(d)three-dimensional graph of accumulating results. 信號檢測性能的Monte Carlo仿真實驗:仍然取上述仿真參數,在不同信噪比下,求恒虛警概率條件下的檢測概率曲線.理論上,對于這里給定的脈寬、帶寬和脈沖個數參數,高斯噪聲中匹配濾波器的增益為10log(2BT)=27.78 d B,多脈沖積累的增益為10log(M)=10 d B,即可檢測到約?37.78 d B的信號,其檢測性能與波形無關.實驗時,采用在距離-多普勒平面上的相干積累峰值作為檢測統計量,無信號時,統計干擾峰值求虛警概率及對應的門限;有信號時,統計計算檢測概率.得到的檢測概率曲線如圖5所示.可以看出,在約?35 d B時,對4種信號的檢測概率均達到80%以上.仿真結果接近理論值,與理論相符. 圖5 4種信號的檢測概率曲線Fig.5.Probability of detection for four kinds of signal in noise as a function of the signal-to-noise ratio. 在尺寸為20 m×8 m×7 m的消聲水池設計實驗方案,進行實驗研究.分別發射仿真實驗的4種信號波形.波形參數為:載頻15 kHz,帶寬10 kHz,采樣頻率100 kHz,脈寬20 ms;脈沖重復周期0.05 s,SNR測量值11.8 dB;進行相干積累,并估計目標的距離、速度參數. 實驗系統組成: NI公司的數據采集儀(使用24 bit的PXIe-4496 AD卡和16 bit的PXI-6733 DA卡),VBF40型放大濾波器,L2線性功放(200 W),寬帶發射換能器,標準水聽器;發射換能器、接收水聽器深度3 m,相距12 m.實驗系統組成如圖6所示. 運動目標回波模擬:采用兩次發射、接收的方法模擬運動目標回波.即對第一次發射、接收的多脈沖數據,人工加入波形壓縮和回波位置走動信息,再進行第二次發射、接收即可.運動信息加入方法:取目標速度v0=?12 kn,由此計算的壓縮因子為1.01,并按照Rm=R0+v0×(m?1)×Tr,計算走動參數,其中R0=12 m,以此對第一次接收的數據重采樣壓縮和循環移位,即可得到包含波形壓縮和距離走動的目標回波. 目標參數估計:對第二次發射、接收的運動目標回波數據進行相干積累,由距離-多普勒平面上積累的峰值位置估計目標距離和速度. 圖6 水池實驗系統組成Fig.6.Experimental arrangement for anechoic water tank. 在消聲水池,所模擬的4種信號的運動目標回波如圖7所示,每種信號的10個回波包含著波形壓縮和距離走動信息.對4種信號的10個回波分別進行相干積累,結果如圖8所示.由積累的峰值位置對目標距離R0、速度v0進行估計,結果如表1所列,這是10次實驗得到的均值和標準差. 可以看出,對4種信號進行相干積累,在距離-多普勒平面上均出現了顯著的峰值,峰值位置出現在目標的初始距離和速度附近.比較4種信號的估計結果可見,CW信號的距離估計誤差大,速度估計精度高,而其余3種信號的距離估計精度高,速度估計誤差大.這是因為CW信號多普勒容限小,脈沖壓縮比大,而其余信號的脈沖壓縮能力強,距離估計精度高. 圖8 4種信號的積累結果 (a)CW信號;(b)LFM信號;(c)m序列編碼信號;(d)Costas編碼信號Fig.8.Accumulating results of four kinds of signals:(a)CW signal;(b)LFM signal;(c)m-sequence phase-coded signal;(d)Costas frequency hop coded signal. 表1 目標初始距離和速度估計結果Table 1.Estimation of initial distance and target velocity. 另外,有必要指出,湖海實驗驗證至關重要,是理論走向實際應用的必要環節.湖海實驗的水聲環境十分復雜,混響、有限帶寬信道及目標運動的不確定性等都會給包絡對齊和多普勒補償帶來困難,從而降低相干積累效果.通過湖海實驗發現問題,克服誤差、干擾影響,優化方法是一項更具挑戰性的研究工作. 通過構建任意發射信號波形的廣義模糊函數來表示多脈沖積累中的匹配濾波器輸出,不僅給出了任意復包絡信號的脈壓信號的一般表達式,而且清楚地表示了多脈沖積累中距離維的距離走動信息和脈沖維的多普勒頻移信息,為距離走動補償、多普勒頻移補償、多普勒模糊補償等相干積累問題分析提供了依據.對于脈壓信號的一般表示式,采用Keystone變換消除距離走動,采用FFT補償多普勒頻移項,實現了任意復包絡信號勻速運動目標回波的長時間相干積累.采用4種不同形式的聲吶波形進行了仿真,得到距離走動補償、多普勒頻移補償、多普勒模糊補償及相干積累的正確計算結果,驗證了對任意復包絡信號進行距離走動補償及相干積累的正確性.信號檢測的Monte Carlo實驗表明相干積累方法的檢測性能與理論分析相符.采用消聲水池實驗進行信號積累,并估計模擬運動目標的距離、速度參數,驗證了方法的有效性. [1]North D O 1963 Proc.IEEE 51 1016 [2]Liu Z L,Liao G S,Yang Z W 2012 Acta Electron.Sin.40 799(in Chinese)[劉志凌,廖桂生,楊志偉 2012電子學報40 799] [3]Zhang L,Sheng J L,Duan J,Xing M D,Qiao Z J,Bao Z 2013 EURASIP J.Adv.Signal Process.2013 33 [4]Dong Q,Zhang L,Xu G,Xing M D 2014 J.Xi’an Jiaotong Univ.48 107(in Chinese)[董祺,張磊,徐剛,邢孟道2014西安交通大學學報48 107] [5]Carlson B D,Evans E D,Wilson S L 1994 IEEE Trans.Aerosp.Electron.Syst.30 102 [6]Carlson B D,Evans E D,Wilson S L 1994 IEEE Trans.Aerosp.Electron.Syst.30 109 [7]Pang C S,Hou H L,Han Y 2012 J.Electron.Infor.Technol.34 754(in Chinese)[龐存鎖,侯慧玲,韓焱2012電子與信息學報34 754] [8]Yu J,Xu J,Peng Y N,Xia X G 2012 IEEE Trans.Aerosp.Electron.Syst.47 1186 [9]Yu J,Xu J,Peng Y N,Xia X G 2012 IEEE Trans.Aerosp.Electron.Syst.47 2473 [10]Yu J,Xu J,Peng Y N,Xia X G 2012 IEEE Trans.Aerosp.Electron.Syst.48 991 [11]Xu J,Xia X G,Peng S B,Yu J,Peng Y N,Qian L C 2012 IEEE Trans.Sig.Proc.60 6190 [12]Perry R P,Dipietro R C,Kozma A,Vaccaro J J 1994 Algorithms for Synthetic Aperture Radar Imagery(Bellingham:SPIE)p160 [13]Perry R P,Dipietro R C,Fante R L 1999 IEEE Trans.Aerosp.Electron.Syst.35 188 [14]Ruan H,Wu Y H,Jia X,Ye W 2013 IEEE Geo.Rem.Sens.Lett.11 128 [15]Zhao Y B,Zhou X P,Wang J 2013 J.Xidian Univ.Nat.Sci.40 98(in Chinese)[趙永波,周曉佩,王娟 2013西安電子科技大學學報自然科學版40 98] [16]Guo B F,Shang C X,Wang J L,Gao M G,Fu X J 2014 Acta Phys.Sin.63 238406(in Chinese)[郭寶鋒,尚朝軒,王俊嶺,高梅國,傅雄軍2014物理學報63 238406] [17]Feng X A,Zhang Y M,Su J J 2014 J.Northwest.Polytechnical Univ.32 882(in Chinese)[馮西安,張楊梅,蘇建軍2014西北工業大學學報32 882] [18]He H,Li J,Petre S 2012 Waveform Design for Active Sensing Systems:A Computational Approach(Cambridge:Cambridge Univ.Press)pp18–25 [19]Zhang Y M 2017 Ph.D.Dissertation(Xi’an:Northwestern Polytechnical University)(in Chinese)[張楊梅2017博士學位論文(西安:西北工業大學)] [20]Guo H W,Liang D N,Wang Y,Huang X T,Dong Z 2003 Proceedings of the 2003 International Society for Optics and Photon.AeroSense Orlando,United States,April 21–25,2003 p1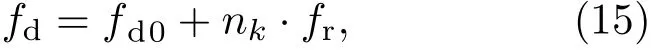
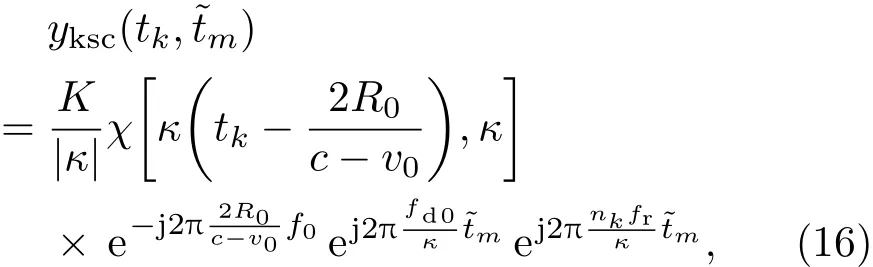
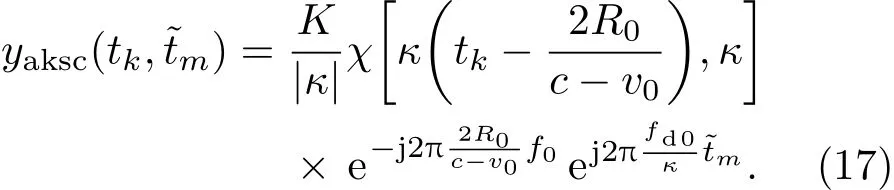
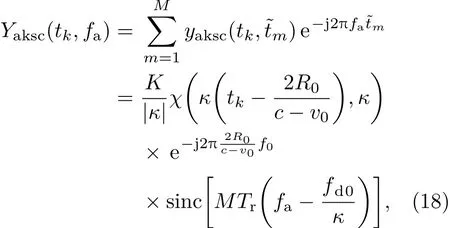
5 實驗驗證
5.1 相干積累的計算機仿真
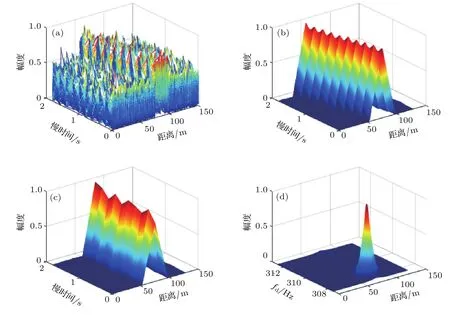
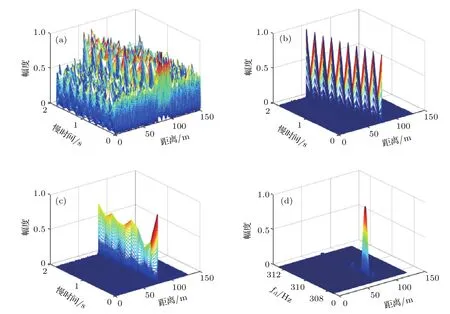
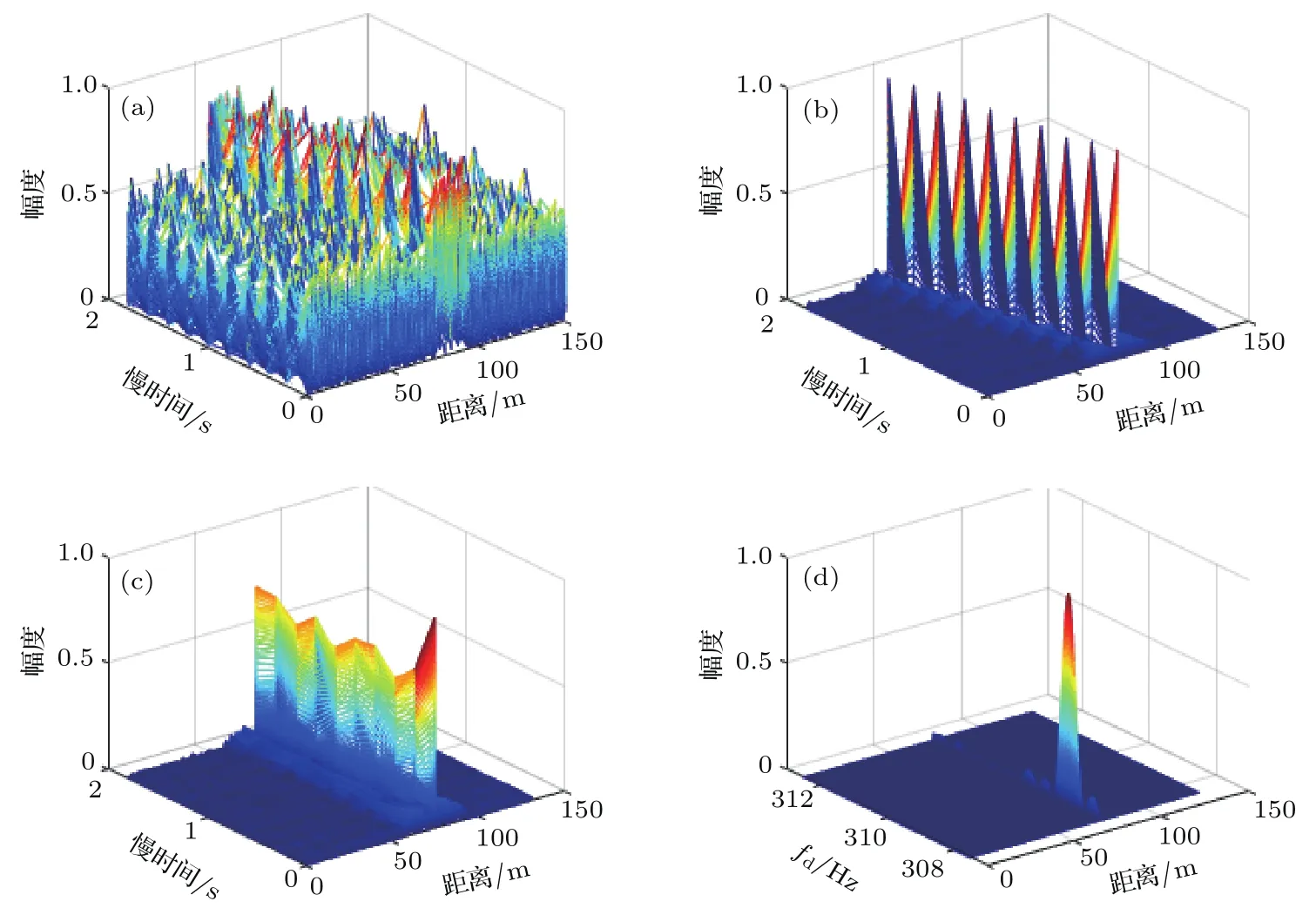
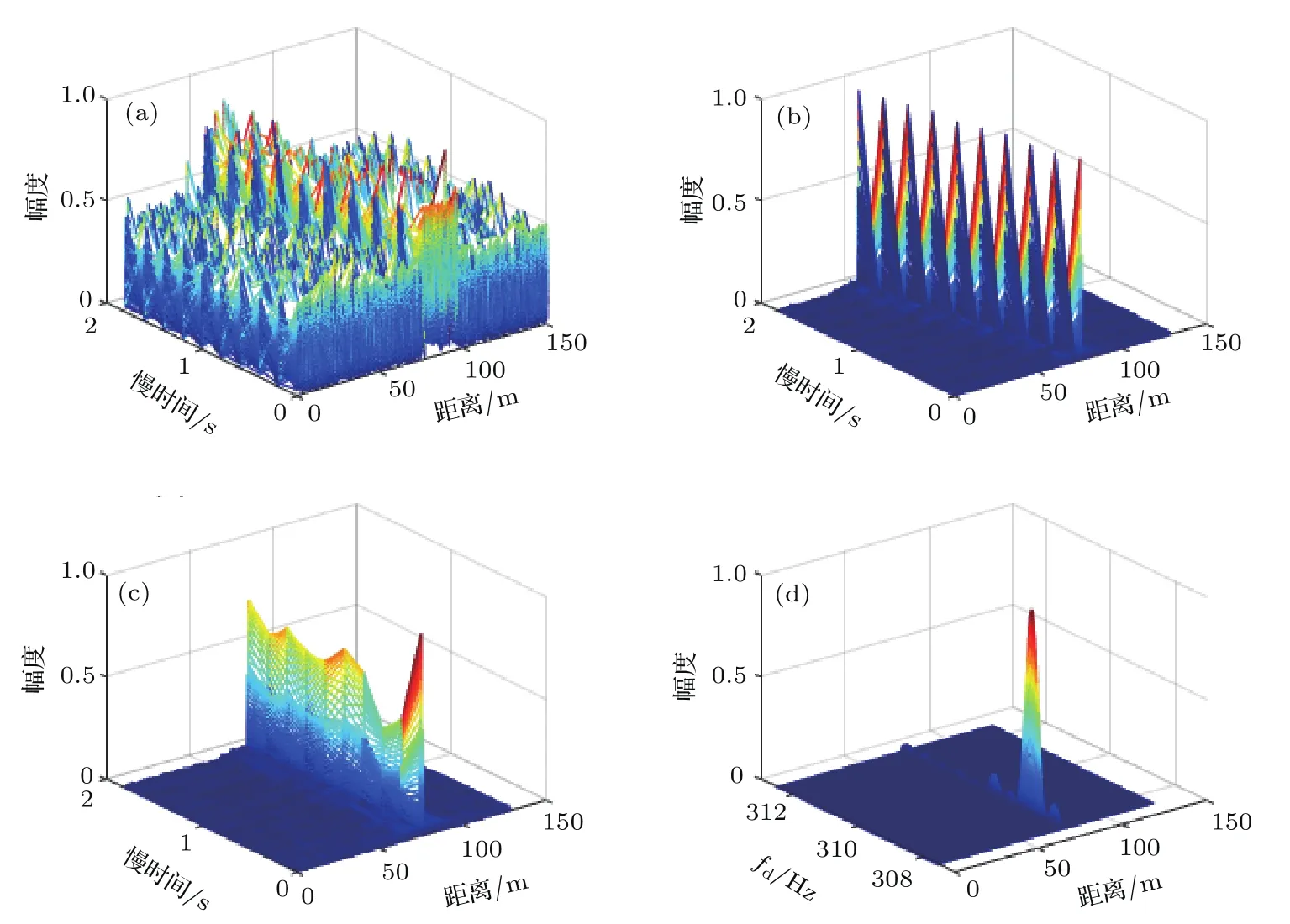
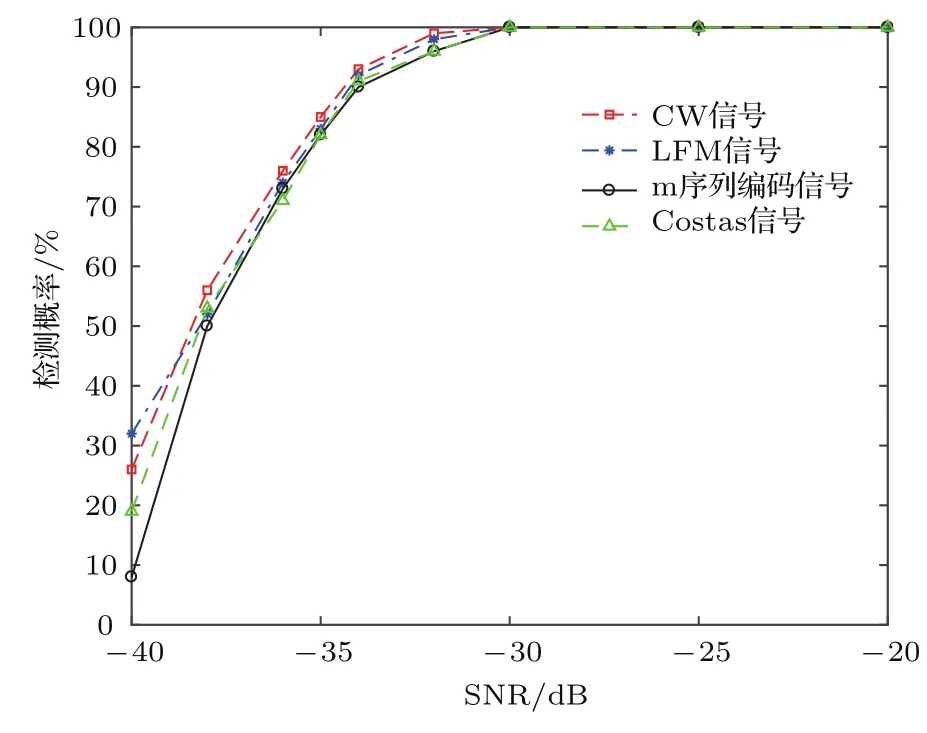
5.2 目標距離、速度估計的消聲水池實驗
6 結 論

