Korteweg-de Vries方程的準孤?立子解及其在離子聲波中的應用

王建勇 程雪蘋 曾瑩 張元祥 葛寧怡

1)(衢州學院教師教育學院,衢州 324000)

2)(浙江海洋大學物理系,舟山 316004)

3)(衢州學院機械工程學院,衢州 324000)

(2017年12月18日收到;2018年1月28日收到修改稿)

1 引 言

Korteweg-de Vries(Kd V)方程是孤子理論的基礎模型之一,它具有非常典型的可積性,如Lax表示[1]、無窮多對稱及守恒律[2]、N-孤子解[3]及Painlevé性質[4]等.KdV方程也是物理學諸多分支學科中一個重要的非線性數學物理模型,在非線性光學、玻色-愛因斯坦凝聚、等離子體物理、生物物理等分支學科中都有著廣泛的應用[5].在等離子體物理中,Kd V方程可描述有限小振幅離子聲波、磁聲波、阿爾文波[6]等.例如,在近期的一項實驗研究報告中,Bandyopadhyay等[7]指出塵埃聲孤立波的振幅和特征寬度隨等離子體參數的變化可由KdV方程的經典孤立子解來描述,而在有限小振幅及低馬赫數條件下,理論結果更是和實驗數據高度符合.

孤子方程的解析解研究是非線性科學中的熱點課題[8,9].最近,通過非局域對稱的局域化及對稱約化,Lou等[10]給出了Kd V方程、非線性Schr?dinger方程等若干孤子方程的孤子-橢圓周期波解,并發現孤子和橢圓周期波之間的相互作用是彈性的,相互作用后兩者僅有相位變化.基于這些方法,Lou[11]又提出了推廣的Painlevé截斷展開法和推廣的tanh函數展開法.應用此類推廣的方法可直接給出孤子與其他非線性波的相互作用解,如孤子與橢圓周期波、Painlevé波、Airy波、Bessel波等的相互作用解[12?20].而在等離子體物理中,人們很早就開始了關于孤子與小振幅周期波之間相互作用的數值研究[21,22].例如,Deeskow等[21]早在1987年就應用數值方法研究了非磁化等離子體中離子聲波和朗繆爾波同時激發的情況,在允許離子擾動和電荷分離條件下,朗繆爾波電場和離子聲波電勢的耦合是一種具有準孤子行為的結構,即朗繆爾波電場可由包絡孤子描述,而離子聲波電勢則以小振幅周期波的形式圍繞在包絡孤子周圍.最近,Keane等[22]也進行了這方面的研究,從包含量子修正的霍爾磁流體力學方程組出發,導出了耦合Zakharov型方程并進行了數值研究,發現初值解形如穿了“衣服”的孤立波,即高斯波峰被小振幅周期波圍繞,并具有在時空演化中保持波形不變的性質.此外,流體力學中已有關于孤立波和小振幅周期波之間相互作用的實驗研究和實際觀測[23?25].例如,Farmer和Smith[24]以及Akylas和Grimshaw[25]曾在加拿大某海灣觀測到了類似孤立波的結構與小振幅周期波之間的相互作用現象.

本文考慮Kd V方程的孤子-橢圓周期波解及其準孤立子行為.應用推廣的tanh函數展開法,給出Kd V方程具有準孤立子行為的兩組孤子-橢圓周期波解及雙孤立子解.另外,運用約化攝動法推導描述離子聲波動力學行為的KdV方程,并由此討論等離子體參數對離子聲準孤立子波形的影響.

2 Kd V方程的準孤立子解

在等離子體物理中,Kd V方程一般可寫為

其中A是非線性項系數,B是色散項系數,兩者由等離子體參數決定.根據推廣的tanh函數展開法,可知KdV方程的解u具有如下截斷展開[14]:

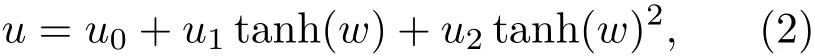
其中ui和w都是關于(x,t)的待定函數.將截斷展開(2)式代入Kd V方程,并令tanh(w)5,tanh(w)4,tanh(w)3的系數為零,可求得u2,u1及u0為：

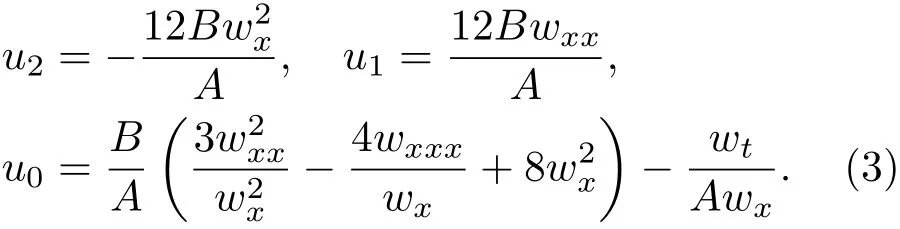
將(3)式代入tanh(w)2的系數方程,可得w的相容性方程

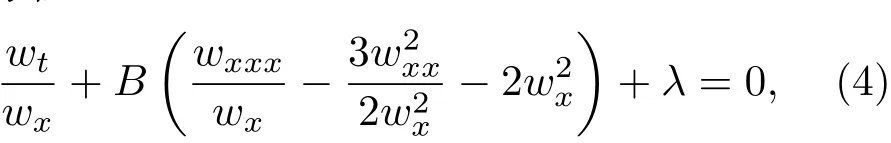
其中λ是積分常數.由(3)式和(4)式,Kd V方程的解(2)可寫為

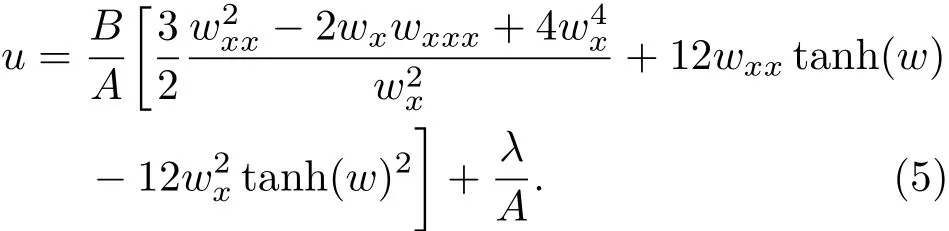
最后,可直接驗證(3)式—(5)式滿足tanh(w)1和tanh(w)0的系數方程.由此說明,若w滿足其相容性方程(4),則(5)式為Kd V方程的解.

為了求得Kd V方程的孤子-橢圓周期波解,可將w設為[26]：

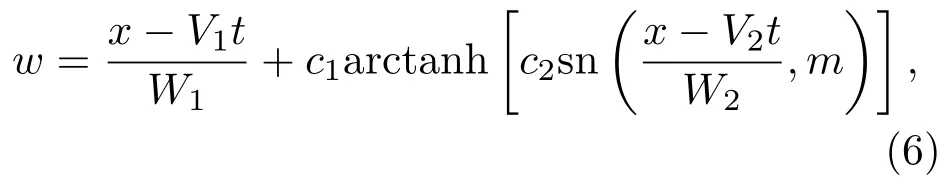
其中sn是Jacobi橢圓正弦函數,m為其模數,V1,V2分別為孤立波和橢圓周期波的速度,W1是孤立波的特征寬度,W2與橢圓周期波波長相關.將關于w的假設(6)式代入相容性方程(4),由Jacobi橢圓函數sn,cn,dn的各階系數可得到關于參數{m,V1,V2,W1,W2,c1,c2,λ}的超定方程組.在這些超定方程組中,若取{m,V1,V2}為任意值,則可求得關于{W1,W2,c1,c2,λ}的參數解.在較早的研究中[26],給出了其中一組參數解:

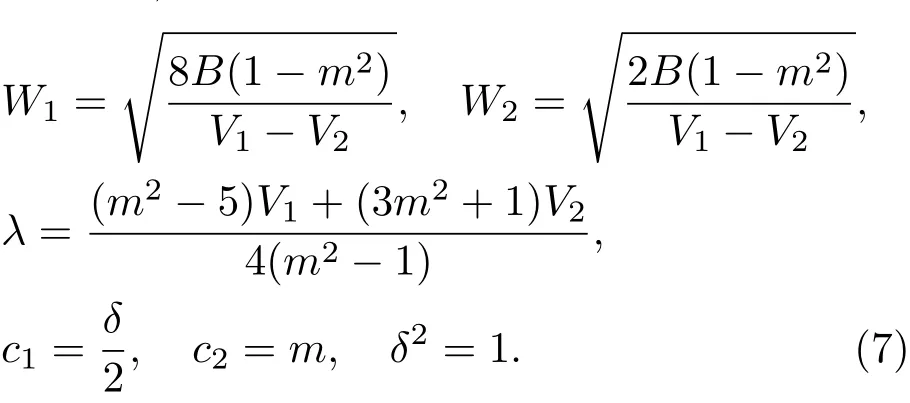
在此參數條件下,Kd V方程的孤子-橢圓周期波解具有比較簡潔的形式:

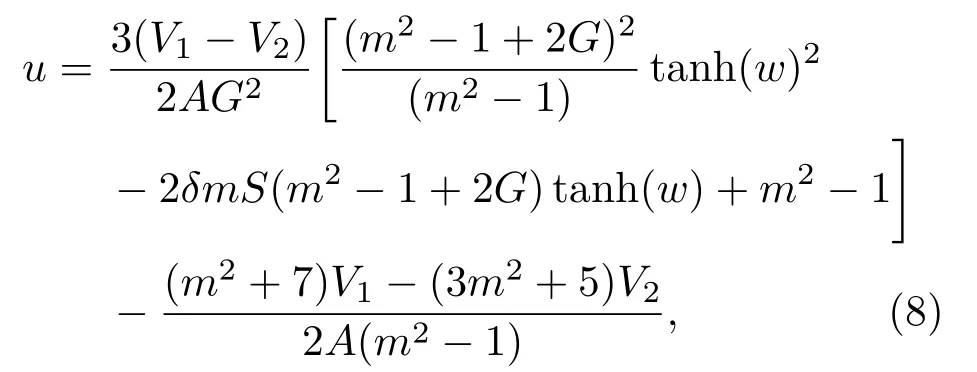
其中

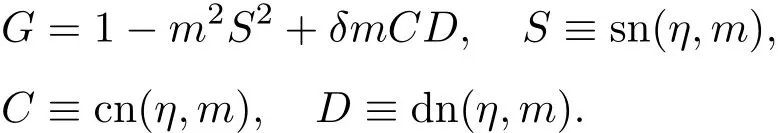
在孤子-橢圓周期波解(8)中,取V1=V,V2=?V及m=0可得滿足零邊界條件的經典孤立子解為:

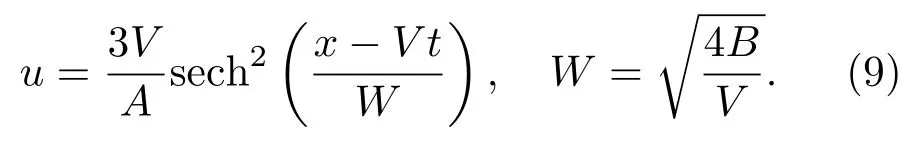
由此不難發現孤子-橢圓周期波解(8)在漸進條件V1=V,V2=?V及m→0下具有準孤立子行為.

研究發現孤子-橢圓周期波解的參數條件也可取為:

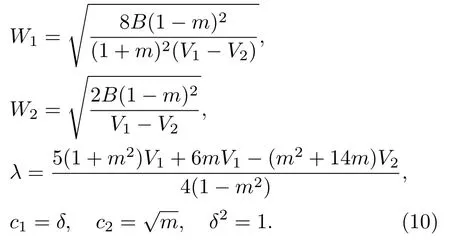
由此參數條件,可得KdV方程的一個新孤子-橢圓周期波解,其形式略為復雜:

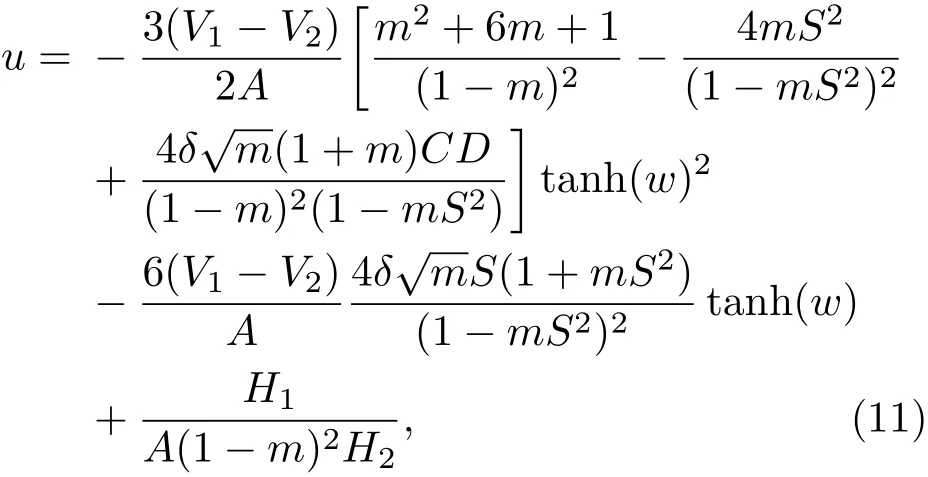
其中H1和H2的具體表達式見附錄A.孤子-橢圓周期波解(11)在漸進條件V1=V,V2= ?V及m → 0下也具有準孤立子行為,下面以圖示說明.準孤立子解(11)與經典孤立子解(9)的對比如圖1所示,由m=0.0016,m=0.0004及經典孤立子解(m=0)的波形對比可知,m取值越小,孤子-橢圓周期波解的孤子核越接近于滿足零邊界條件的經典孤立子,而圍繞在其周圍的橢圓周期波也越接近于在零附近振蕩的正余弦波.Kd V方程的孤子-橢圓周期波解(8)式和(11)式都具有準孤立子行為,可統稱為準孤立子解.

顯然,在參數條件(7)式和(10)式中,m都不可取為1.因此,孤子-橢圓周期波解(8)和(11)式都無雙孤立子極限.為求得雙孤立子解,可將w設為：

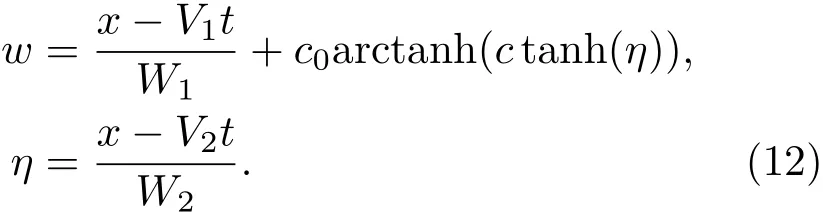
將(12)式代入相容性方程(4),令tanh(η)的各階系數為零,可求得關于{c0,W1,W2,λ}的參數解：

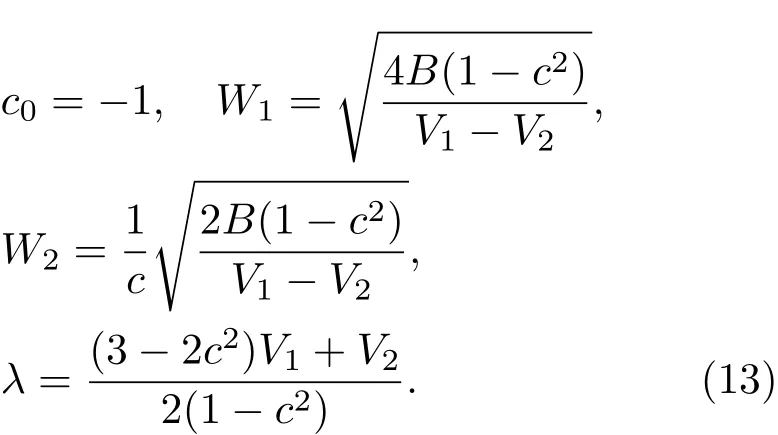
由(5)式,(12)式及(13)式,可給出KdV方程的雙孤立子解：

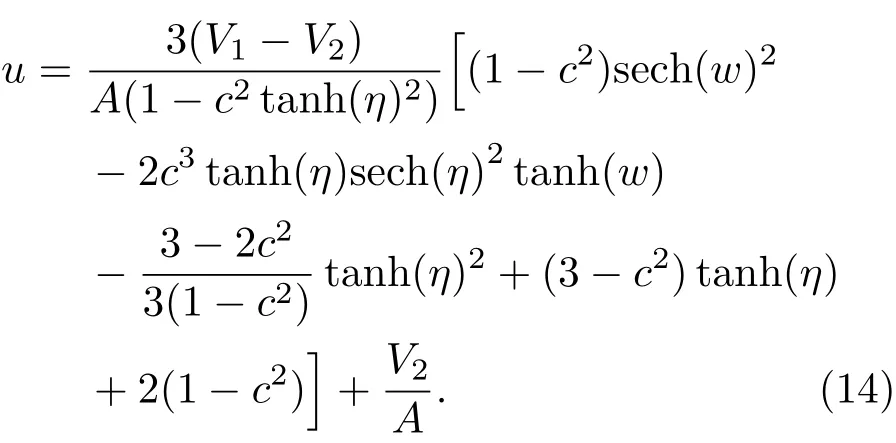
圖2是由(14)式描述的雙孤立子追趕相互作用,其中高瘦孤立波的波速為V1=1.25,矮胖孤立波的波速為V2=0.75.由圖2可知,兩孤立波在發生追趕相互作用后并不改變原有的波形與波速,僅發生相位變化.

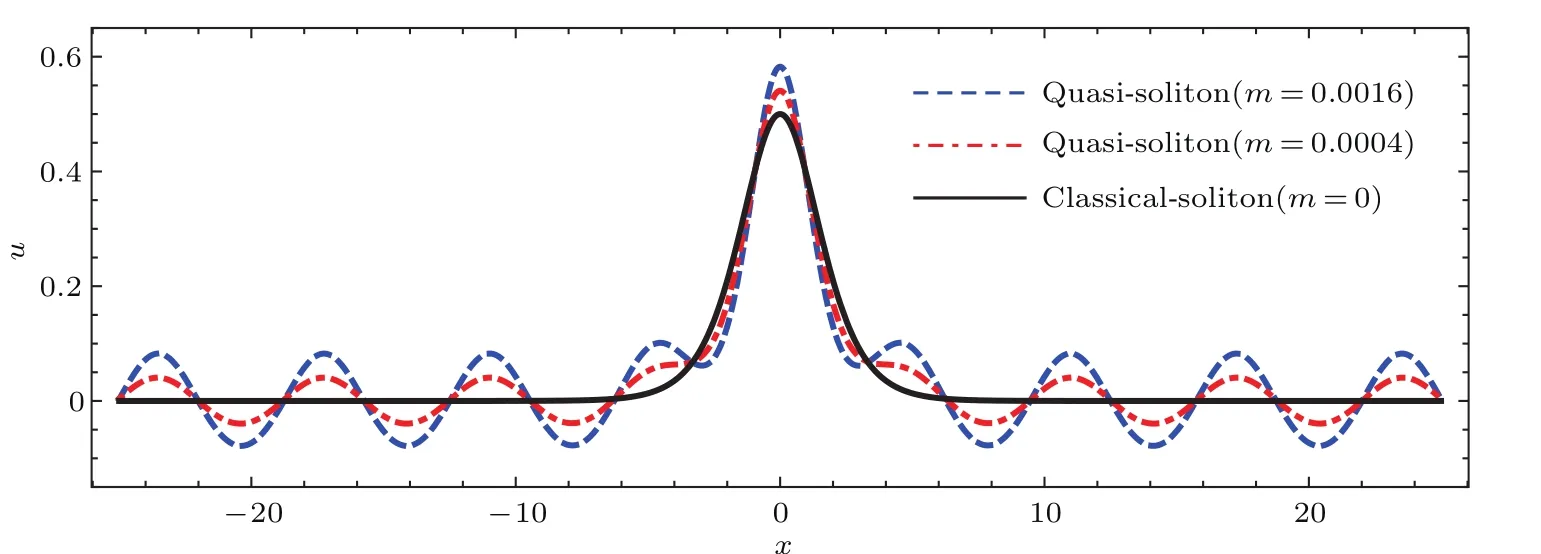
圖1 準孤立子解(11)與經典孤立子解(9)的對比 波參數為V1=1,V2=?1,V=1及δ=1,Kd V方程的系數為A=6,B=1Fig.1.Comparison of quasi-soliton solution(11)with the classical solion solution(9).Wave parameters are selected as V1=1,V2=?1,V=1,δ=1 and coeffi cients of the Kd V eqation are A=6,B=1.

圖2 由(14)式給出的雙孤立子相互作用 波參數為V1=1.25,V2=0.75及c=0.75,Kd V方程的系數為A=6,B=1Fig.2.Two soliton interaction given by equation(14).Wave parameters are selected as V1=1.25,V2=0.75,c=0.75 and coeffi cients of the Kd V eqation are A=6,B=1.

3 描述離子聲波動力學行為的KdV方程

考慮均勻磁化等離子中的離子聲波,等離子體的成分是超熱電子和熱離子.相對于離子,電子質量極小,可忽略電子慣性.假設等離子體沉浸在恒定磁場B=B0?z中,?z是單位矢量.平衡態時,由電中性可知ne0=ni0=n0,ne0,ni0分別是平衡態時的電子、離子數密度.另外,假設超熱電子遵循κ分布

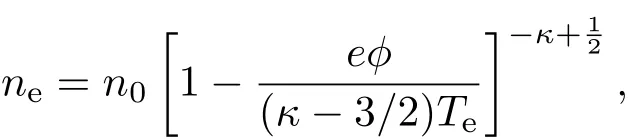
其中,參數κ(κ>3/2)是表征電子分布偏離麥克斯韋分布程度的物理量.

在上述條件下,離子聲波的動力學行為可由連續性方程、動量方程和泊松方程來描述:

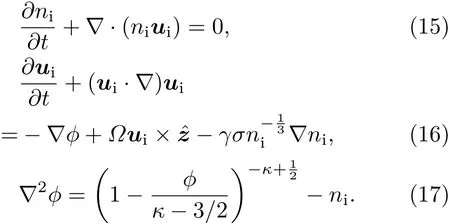
(15)式—(17)式中,ni是熱離子的粒子數密度,由平衡態離子數密度n0無量綱化;ui是由離子聲速Cs=(Te/mi)(1/2)無量綱化后的離子流體速度;電勢?則由Te/e無量綱化;時間變量和空間變量分別經離子等離子體離子頻率的倒數 ωp?i1=和德拜長度無量綱化;離子回旋頻率經離子等離子體頻率ωpi無量綱化;σ=Ti/Te是離子電子溫度比.對于低頻離子聲波過程,可認為電子是絕熱的,動量方程(16)式中的絕熱系數可取為γ=5/3.此外,對于有限小振幅波?1,泊松方程可做如下近似展開:

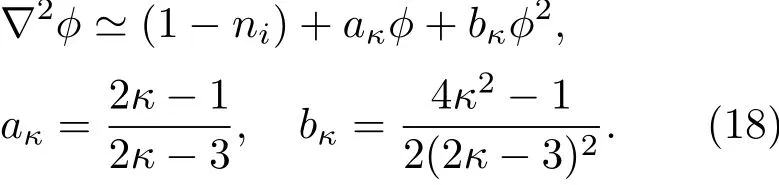
下面應用約化攝動法來研究磁化超熱電子-熱離子中的有限小振幅離子聲波.首先引入坐標變換

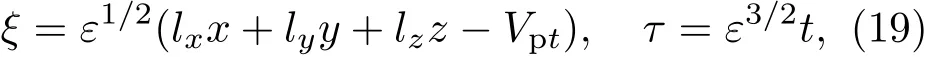
其中ε?1是描述弱色散效應的無窮小參數,Vp是待定離子聲波相速度;lx,ly,lz是波矢量k沿x,y,z方向的余弦值,且lx,ly,lz滿足l2x+l2y+l2z=1.由于磁場在各個方向的非均勻性,相對于平行于磁場方向的離子流體速度分量,離子流體速度沿垂直于磁場方向的分量應在ε的更高階次.故可將獨立變量在平衡態附近按ε的冪次展開為:

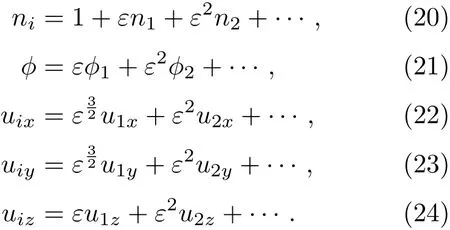
將(20)式—(24)式代入流體力學方程組(15)式—(17)式并收集ε的各階系數,可得到關于各階擾動量的相容性方程.由ε的最低冪次,可求得n1,u1x,u1y及u1z為

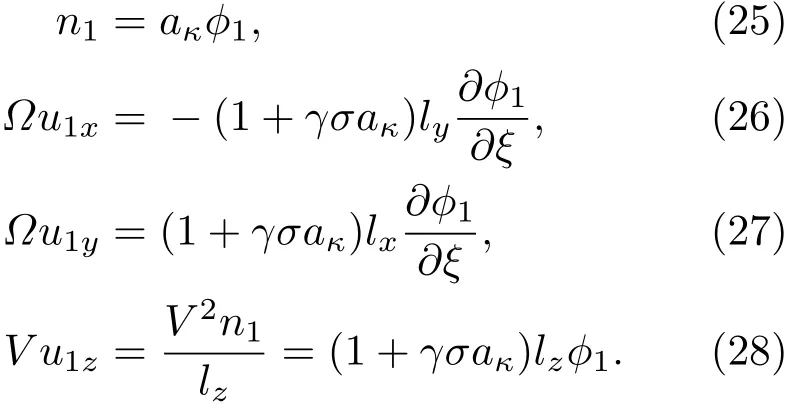
由(25)式—(28)式可給出離子聲波的相速度Vp為

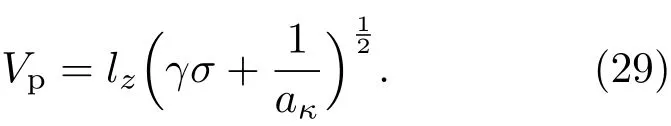
由(29)式可知,當離子電子溫度比σ增加時,離子聲波相速度增加;當磁場方向與波矢量方向的夾角增加時(lz減小),離子聲波相速度減小;當電子偏離麥克斯韋分布的程度增加時(κ減小),aκ增大,離子聲波相速度減小.

由ε的高一階冪次的系數,可得關于二階小量的相容性方程.代入(25)式—(29)式可求得:

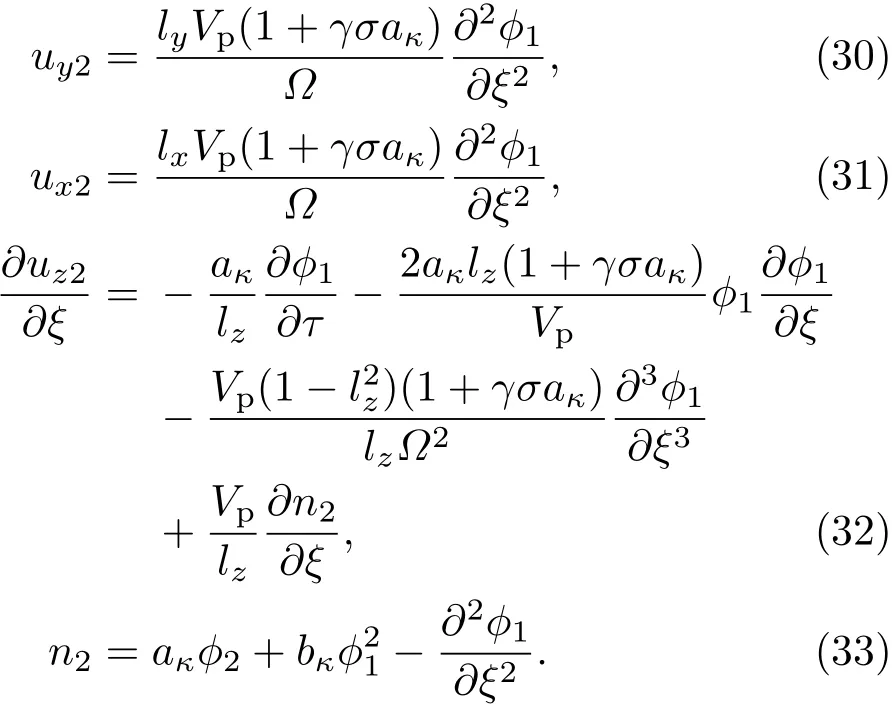
由(30)式—(33)式的相容性,可給出KdV方程

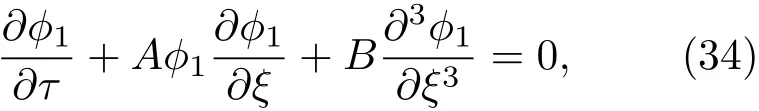
其中,非線性項系數A和色散項系數B為:

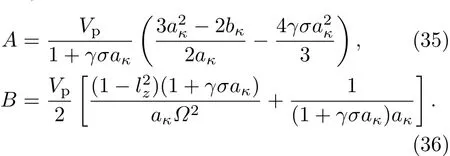
4 等離子體參數對波形的影響

由于Kd V方程的非線性項系數A和色散項系數B由等離子體物理參數決定,故等離子體參數的變化會引起孤子核的特征寬度和振幅的變化,同樣也會引起圍繞在其周圍的小振幅周期波的波長和振幅的變化.下面討論在實驗室坐標系中等離子體參數對離子聲準孤立子波形的影響.在(21)式中,忽略高階小量,可取?=ε?1.由(8)式及(19)式,不難給出電勢離子聲準孤立子在實驗室坐標系下的表達式.

首先,考慮電子分布偏離麥克斯韋分布的程度(κ)對離子聲準孤立子波形的影響.對于遵循κ分布的電子,當κ減小時,超熱電子成分增加,電子偏離麥克斯韋分布的程度增加;當κ增大時,超熱電子成分減少,電子偏離麥克斯韋分布的程度減小.圖3為離子聲準孤立子波形隨電子分布偏離麥克斯韋分布程度(參數κ)的變化,由圖可知,當κ增大時,即電子分布偏離麥克斯韋分布的程度減小時,孤子核的振幅和特征寬度都增大,圍繞在孤子核周圍的小振幅周期波的振幅和波長也都增大.當κ→∞時,電子遵循麥克斯韋分布,孤子核的振幅和特征寬度、小振幅周期波的振幅和波長達到最大值.這種現象說明,當超熱電子變得越來越稀疏時(κ增大),Kd V方程的非線性項系數A減小而色散項系數B增大,進而使孤子核的振幅和特征寬度、小振幅周期波的振幅和波長都增大.從物理上來講,離子聲波由電子熱壓強提供驅動力,而κ增大的過程也可視為電子熱壓強增加的過程,從而使孤子核的振幅和特征寬度、小振幅周期波的振幅和波長都增大.文獻[27]研究了電子分布參數κ對經典孤立子波形的影響,研究表明κ增大將導致經典孤立子的振幅和特征寬度都增大;而當κ→∞時,經典孤立子的振幅和特征寬度達到最大值,其研究結果與本文一致.

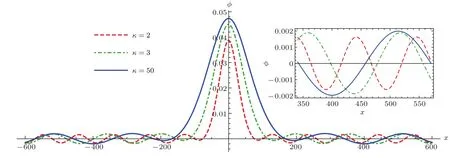
圖3 離子聲準孤立子波形隨電子分布偏離麥克斯韋分布程度(參數κ)的變化 波參數為ε=0.1,m=0.02,δ=?1,V1= ?V2=0.05,? =0.3,σ=0.01,l x=0.5及l z=0.3Fig.3.Variation of the ion acoustic(IA)quasi-soliton structure with respect to the electron superthermalityκ.Wave parameters areε=0.1,m=0.02,δ=?1,V1=?V2=0.05,? =0.3,σ=0.01,l x=0.5 and l z=0.3.

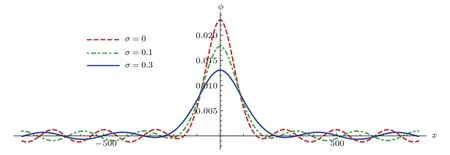
圖4 離子聲準孤立子波形隨離子與電子之間溫度比σ=T i/T e的變化 波參數為ε=0.05,m=0.025,δ=?1,V1=?V2=0.05,l x=0.5,l z=0.3,?=0.3及κ=3Fig.4.Variation of the IA quasi-soliton structure with respect to the ion to electron temperature ratioσforε=0.05,m=0.025,δ=?1,V1=?V2=0.04,l x=0.5,l z=0.3,? =0.3 andκ=3.

其次,考慮離子電子溫度比(σ)對離子聲準孤立子波形的影響.圖4為離子聲準孤立子波形隨離子與電子之間溫度比σ=Ti/Te的變化,由圖可知,當離子與電子之間溫度比σ=Ti/Te減小時,孤子核振幅、周期波振幅增大,孤子核特征寬度、周期波波長減小;當離子為冷離子,即σ=0時,孤子核振幅、周期波振幅達到最大值,而孤子核特征寬度、周期波波長達到最小值.這種現象說明,當離子與電子之間溫度比σ減小時,Kd V方程的非線性項系數A和色散項系數B都減小,進而使孤子核振幅、周期波振幅增大,孤子核特征寬度、周期波波長減小.文獻[28]研究了離子與電子之間溫度比對經典孤立子的影響,發現離子電子溫度比σ=Ti/Te減小時,經典孤立子的振幅將增大而特征寬度將減小,此結果與圖4孤子核的波形變化一致.

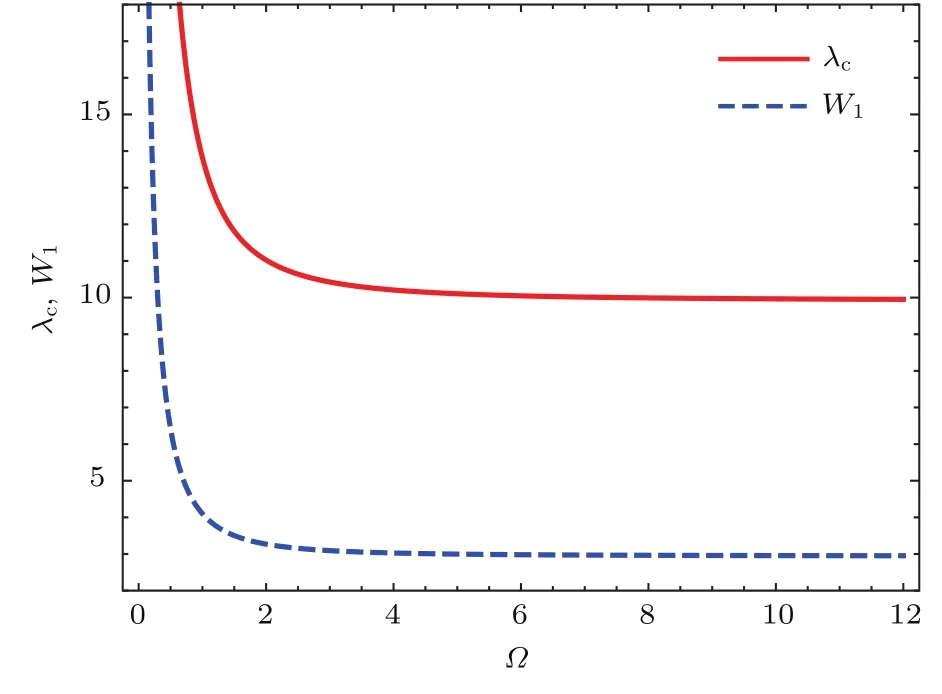
圖5 孤子特征寬度及周期波波長隨磁場大小?的變化波參數為m=0.02,δ=1,V1=?V2=0.05;等離子體參數為σ=0.01,l z=0.3及κ=50Fig.5.Variation of soliton width and wavelength of periodic wave with respect to the electron magnetic fi eld strength? for m=0.02,δ=1,V1=?V2=0.05 and plasma parameters areσ=0.01,l z=0.3 and κ=50.

第三,考慮離子聲準孤立子波形隨磁場大小?的變化.由(35)和(36)式可知,非線性項系數A與磁場大小?無關,因此,孤子核振幅、周期波振幅與磁場大小?變化無關.下面僅討論磁場大小?對孤子核特征寬度、周期波波長的影響.(7)式給出了孤子核特征寬度表達式,文獻[26]由“穿衣服”結構給出了周期波波長為λc=4K(m)W2,K(m)是第一類Legendre完全橢圓積分,由此可做圖討論.圖5為孤子特征寬度及周期波波長隨磁場大小?的變化,由圖可知,當磁場取值較小時,?增大將導致孤子核特征寬度、周期波波長顯著減小.當?進一步增大時,孤子核特征寬度、周期波波長都將趨向一固定值.此現象可由KdV方程色散項系數的表達式給出解釋.當磁場大小?達到極限,即(1?l2z)(γσ+1/aκ)? ?2時,色散項系數B可近似取為

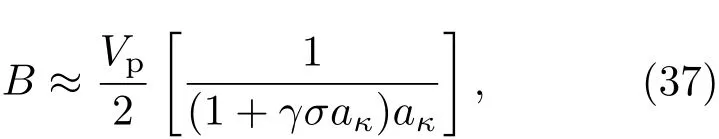
此時,色散項系數B與?無關,故孤子核特征寬度、周期波波長存在極限值.文獻[27,29]考慮了磁場大小?對經典孤立子的影響,也發現磁場大小?對孤子特征寬度的影響存在一個極限值.

最后,討論離子聲準孤立子波形隨磁場方向與波矢量之間夾角的變化.圖6為離子聲準孤立子波形隨傾斜程度lz的變化,由圖可知,當磁場B與波矢量k之間夾角θ增大時,lz減小,孤子核振幅、周期波振幅增大,孤子核特征寬度、周期波波長減小.當磁場B與波矢量k之間夾角為直角時,lz為零,孤子核振幅、周期波振幅達到最大值,孤子核特征寬度、周期波波長達到最小值.

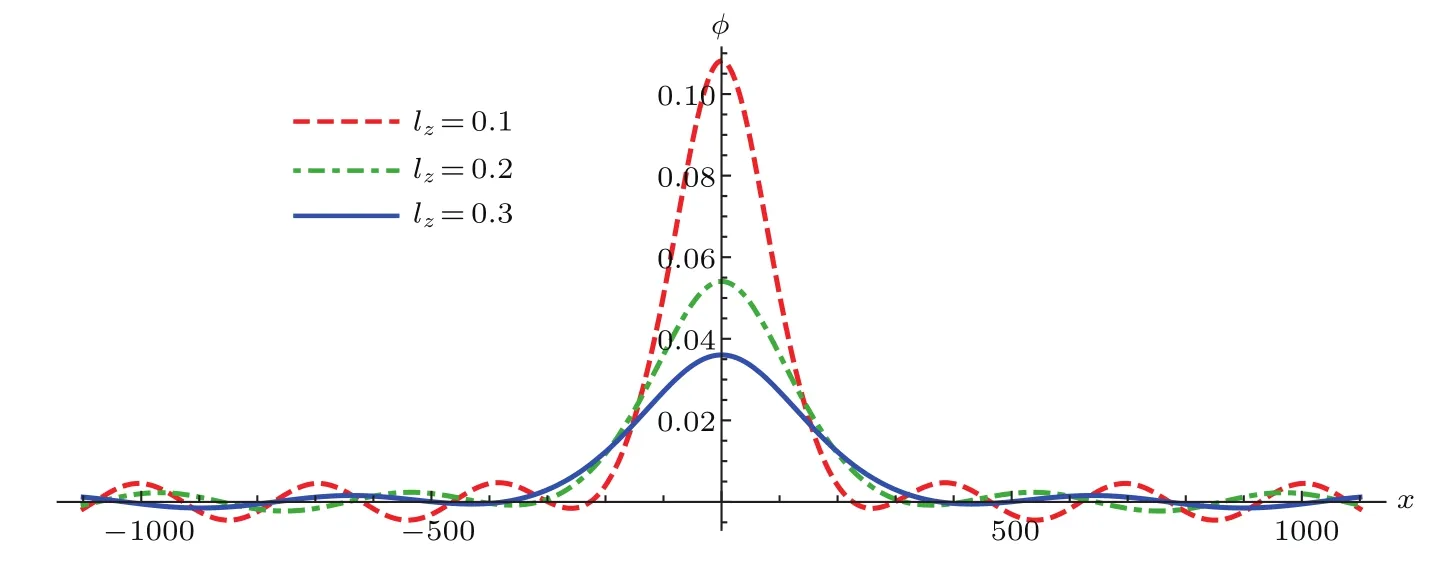
圖6 離子聲準孤立子波形隨傾斜程度l z的變化 波參數為ε=0.1,m=0.02,δ=?1,V1=?V2=0.04,l x=0.5,?=0.3,σ=0.01及κ=3Fig.6.Variation of the IA quasi-soliton structure with respect to obliqueness l z forε=0.1,m=0.02,δ=?1,V1=?V2=0.04,l x=0.5,? =0.3,σ=0.01 andκ=3.

5 結 論

本文應用推廣的tanh函數展開法給出了KdV方程具有準孤立子行為的兩組孤子-橢圓周期波解,其中一組為新解.討論了均勻磁化等離子體中描述離子聲波動力學行為的準孤立子,發現電子分布偏離麥氏分布、離子電子溫度比、磁場大小和磁場方向對離子聲準孤立子波形具有顯著影響.本文給出的準孤立子解可應用到物理學的眾多領域.例如,可將準孤立子解視為“穿衣服”孤立子,并在實驗和數值研究中給出經典孤立子解的修正.

附錄A

H1和H2的具體表達式為:

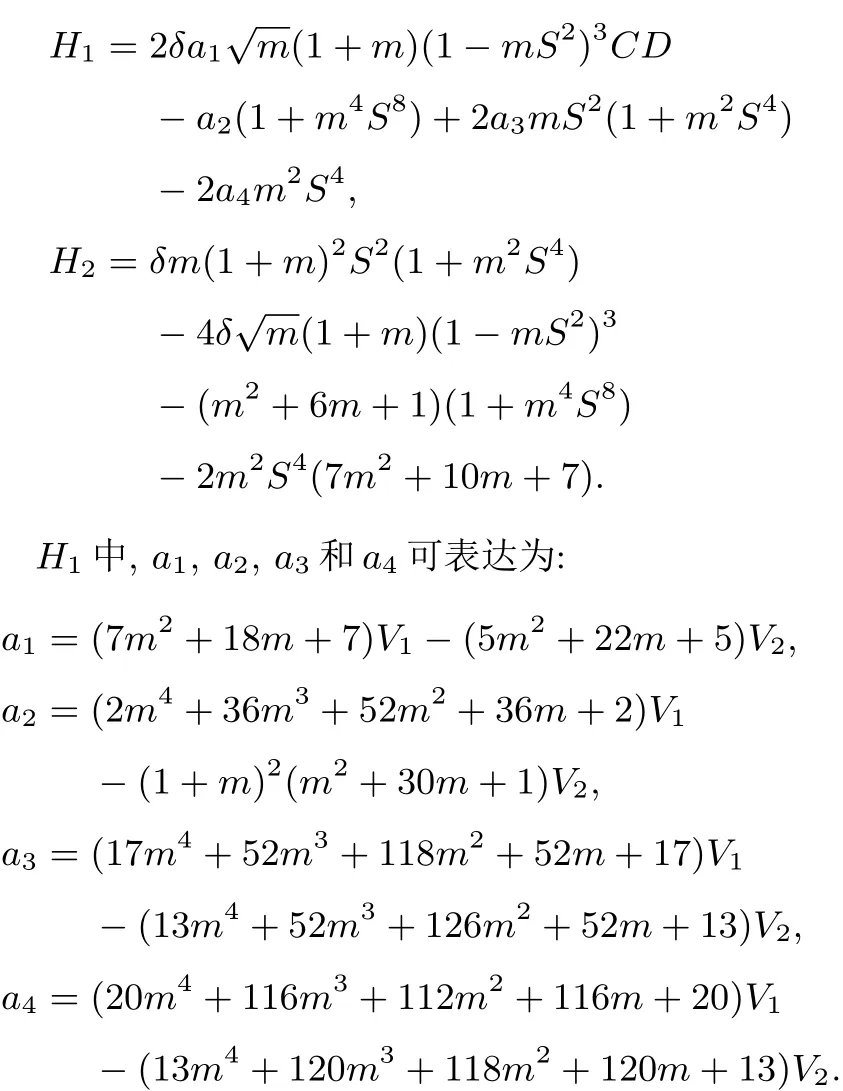
[1]Lax P D 1968 Commun.Pur.Appl.Math.21 467

[2]Miura R,Gardner C,Kruskal M 1968 J.Math.Phys.9 1204

[3]Hirota R 1971 Phys.Rev.Lett.27 1192

[4]Weiss J,Tabor M,Carnevale G 1983 J.Math.Phys.25 522

[5]Dauxois T,Peyrard M 2006 Physics of Solitons(Cambridge:Cambridge University Press)

[6]Jeff rey A,Kakutani T 1972 SIAM Rev.14 582

[7]Bandyopadhyay P,Prasad G,Sen A,Kaw P K 2008 Phys.Rev.Lett.101 065006

[8]Cheng X P,Li J Y,Xue J R 2011 Acta Phys.Sin.60 110204(in Chinese)[程雪蘋,李金玉,薛江蓉2011物理學報60 110204]

[9]Mao J J,Yang J R,Li C Y 2012 Acta Phys.Sin.61 020206(in Chinese)[毛杰健,楊建榮,李超英2012物理學報61 020206]

[10]Lou SY,Hu X R,Chen Y 2012 J.Phys.A:Math.Theor.45 155209

[11]Lou S Y 2015 Stud.Appl.Math.134 372

[12]Tang X Y,Hao X Z,Liang Z F 2017 Comp.Math.Appl.74 1311

[13]Tang X Y,Liang Z F,Wang J Y 2015 J.Phys.A:Math.Theor.48 285204

[14]Gao X N,Lou S Y,Tang X Y 2013 JHEP 05 029

[15]Chen C L,Lou S Y 2013 Chin.Phys.Lett.30 110202

[16]Cheng X P,Lou S Y,Chen C L,Tang X Y 2014 Phys.Rev.E 89 043202

[17]Ren B,Cheng X P,Lin J 2016 Nonlinear Dyn.86 1855

[18]Ren B 2017 Commun.Nonlinear Sci.Numer.Simul.42 456

[19]Hao X Z,Liu Y P,Tang X Y,Li Z B 2016 Comp.Math.Appl.72 2405

[20]Wang J Y,Cheng X P,Tang X Y,Yang J R,Ren B 2014 Phys.Plasmas 21 032111

[21]Deeskow P,Schamel H,Rao N N,Yu M Y,Varma R K,Shukla P K 1987 Phys.Fluids 30 2703

[22]Keane A J,Mushtaq A,Wheatland M S 2011 Phys.Rev.E 83 066407

[23]Davis R E,Acrivos A 1967 J.Fluid Mech.29 593

[24]Farmer D M,Smith J D 1980 Deep-sea Rea.27A 239

[25]Akylas T R,Grimshaw R H J 1992 J.Fluid Mech.242 279

[26]Wang J Y,Tang X Y,Lou S Y,Gao X N,Jia M 2014 Europhys.Lett.108 20005

[27]Williams G,Kourakis I 2013 Plasma Phys.Controlled Fusion 55 055005

[28]Singh S V,Devanandhan S,Lakhina G S,Bharuthram R 2013 Phys.Plasmas 20 012306

[29]Saini N S,Kourakis I 2010 Plasma Phys.Controlled Fusion 52 075009