廣義不完備多粒度標記決策系統的粒度選擇

吳偉志 楊 麗 譚安輝 徐優紅

(浙江海洋大學數理與信息學院 浙江舟山 316022) (浙江省海洋大數據挖掘與應用重點實驗室(浙江海洋大學) 浙江舟山 316022) (wuwz@zjou.edu.cn)

粒計算(granular computing, GrC)是當前人工智能領域中一個非常活躍的研究方向，是信息處理的一種新的概念和計算范式，它模擬人類思考模式，以粒(granule)為基本計算單位，強調對現實世界問題多視角、多層次的理解和描述，是針對復雜問題求解、海量數據挖掘和不確定性信息處理等問題研究的有力工具.早在1979年，模糊數學的創始人Zadeh[1]就提出了信息粒度(information granularity)的概念.Hobbs[2]于1985年對粒度(granularity)概念作了進一步的闡述，描述了粒計算雛形的一些基本特征，以不同的粒度來概化世界，以粒度之間的交換來處理問題.Zadeh[3]于1997年又進一步提出了信息粒化(information granulation)的概念，并認為人類認知能力可概括為粒化、組織和因果3個主要特征.而“粒計算”這個概念是Lin[4]于1997年首次提出的，后來Lin[5]和Yao[6]分別對粒計算研究的一些基本問題進行了闡述.我國張鈸院士和張鈴教授[7]提出的商空間(quotient space)理論被公認為粒計算的另一個重要模型，該理論明確指出“在問題求解研究中，人類智能的一個公認特點，就是人們能從極不相同的粒度上觀察和分析同一問題”.

迄今為止，已經提出了很多涉及具體應用背景的粒計算模型和方法，而在眾多粒計算研究方法中，粗糙集對粒計算研究的推動和發展起著重要的作用[8-19].粗糙集數據分析中的典型數據描述結構稱為信息系統(information system)[20]，又稱為信息表或對象-屬性值表，信息表所給出的是數據集的訓練樣本，原始的Pawlak粗糙集理論利用樣本集上的等價類來描述“粒度”，用等價關系所誘導的劃分來描述粒度空間.由于Pawlak粗糙集模型所用到的等價關系要求過于嚴厲且對噪聲過于敏感，因此，很多基于非等價關系的粗糙集模型被提出來，并用于各種類型的信息系統和決策表的信息粒度表示和知識獲取問題[9-11,16-18].然而，在傳統粗糙集數據分析中，信息系統或決策表中的每個對象只能取唯一的屬性值，這樣的信息系統所描述的是固定尺度下的對象信息，我們稱之為單粒度標記信息系統.事實上，單一粒度框架下的知識表示以及數據處理方法已遠遠不能滿足實際應用的需求，因而“多粒度”已經成為粒計算研究方向的熱點.將復雜問題轉換為多粒度問題并利用多粒度方法進行求解，不僅體現了粒計算中將復雜問題分層、分塊處理的基本思想，而且展現出人類的多層次、多視角思維認知能力.在粗糙集數據分析方面，錢宇華等人在文獻[21]中首次提出了多粒度粗糙集模型，這是一種推廣的Pawlak粗糙集模型，所提出的樂觀粗糙集和悲觀粗糙集思想有較好的創新性，其主要思想是通過屬性的選擇進行交運算或并運算進行數據處理，在此基礎上針對不同數據背景的多粒度粗糙集方法被相繼提出[22-23].在實際應用中人們可能要在不同的粒度標記下對同一對象在同一屬性或變量下對系統中的數據進行觀察、表示、分析和做出決策，即對于同一個對象和所對應的某個屬性，根據實際問題的不同粒度層次的需要，可以取不同層次標記的值.比如，對于地圖上我國的某一地方，根據行政區域的不同粒度層次(如鄉、縣、地級市、省自治區等級別)，其所屬地分別給予不同的區域標記.針對類似問題，Wu和Leung在文獻[24]中首次提出了基于多粒度標記劃分的粗糙集數據分析方法，在這種多粒度標記數據模型下，同一批數據可以被標記為不同的粒度層次，人們可以根據需要在不同的粒度標記層面上處理和分析數據.Wu等人[25-29]還進一步研究了在多粒度標記框架下的其他數據類型的信息粒度表示和最優粒度的選擇問題，She等人[30]提出了多粒度標記決策系統的局部最優粒度選擇和規則提取方法.Gu和Wu[31-32]還給出了協調的和不協調的多粒度標記決策系統中知識獲取的算法.由于人們在日常生活中接觸和處理的數據很多情形下都有缺省的情況，針對此類情況，Wu等人[33]最近又進一步提出了不完備多粒度標記粗糙集數據分析模型.然而，以上多粒度標記信息系統都有一個共同的假設，即系統中所有的屬性都具有相同的粒度標記個數，而實際生活中人們可能面對不同的屬性具有不同的粒度標記個數的數據處理問題，針對這種情形，Li和Hu在文獻[34]中提出了一種推廣的多粒度標記數據分析模型，研究了不同屬性具有不同粒度標記層次的多粒度標記決策系統的最優粒度選擇問題，給出了2種最優粒度標記選擇方法.

本文結合文獻[33-34]的思路，提出推廣的不完備多粒度標記決策系統的粗糙集知識表示模型，并討論該模型下粒度標記選擇問題.

1 相關的基礎知識

設U是非空論域，U的子集全體記為P(U).對于A∈P(U)，A在U中的補集記為～A，即～A={x∈U|x?A}.本節簡單介紹一些基本概念與知識.

1.1 不完備信息系統

一個信息系統是一個二元組(U,AT)，其中U={x1,x2,…,xn}是一個非空有限對象集，稱為論域；AT={a1,a2,…,am}是一個非空有限屬性集，對于任意的a∈AT，滿足a:U→Va，即a(x)∈Va，x∈U，其中Va={a(x)|x∈U}稱為a的值域.

當一個信息系統中的一些屬性值是缺省的或者說是未知的，則稱該系統為不完備信息系統，我們仍然用二元組(U,AT)來表示.用符號“*”表示未知值或缺省值，即如果a(x)=*，那么就認為x在屬性a上的值是未知的.

對于給定的一個不完備信息系統(U,AT)，A?AT，記：

RA={(x,y)∈U×U|?a∈A,a(x)=a(y)
或a(x)=*或a(y)=*}.

顯然，RA是自反和對稱的，即RA是相似關系，但一般是非傳遞的.記：

SA(x)={y∈U|(x,y)∈RA}，x∈U.

SA(x)稱為對象x關于RA的相似類，記:

URA={SA(x)|x∈U}.

設(U,AT)是一個不完備信息系統，A?AT，X?U，X關于RA的下近似和上近似定義如下：

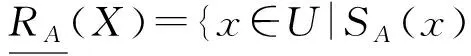
其中，|X|表示集合X的基數.X關于RA的粗糙度為

1.2 信任函數與似然函數

定義1. 信任結構.設U是非空有限論域，集函數m:P(U)→[0,1]稱為mass函數(基本概率指派)，若它滿足2個性質：

1)m(?)=0；

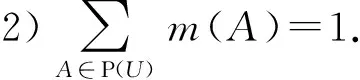
稱A∈P(U)是m的焦元，若m(A)>0.記M={A∈P(U)|m(A)>0},則序對(M,m)稱為U上的一個信任結構.

定義2. 信任函數與似然函數.設(M,m)是U上的一個信任結構，集函數Bel:P(U)→[0,1]稱為U上的信任函數，若

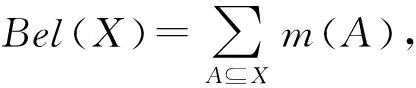
集函數Pl:P(U)→[0,1]稱為U上的似然函數，若

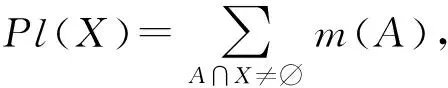
由同一信任結構導出的信任函數與似然函數是對偶的，即?X∈P(U)，

Pl(X)=1-Bel(～X)，

且

Bel(X)≤Pl(X).

反之，信任結構中的mass函數可以通過M?bius變換用信任函數來表示，即?X∈P(U)，

信任函數和似然函數還可以等價地用公理定義，即集函數Bel:P(U)→[0,1]是U上的一個信任函數當且僅當它滿足3個性質：

1)Bel(?)=0；

2)Bel(U)=1；

3) 對于任意X1,X2,…,Xl?U,有

同樣地，Pl:P(U)→[0,1]是U上的一個似然函數當且僅當它滿足3個性質：

1)Pl(?)=0；

2)Pl(U)=1；

3) 對于任意X1,X2,…,Xl?U,有:

定理1[35]. 設(U,AT)是一個不完備信息系統，A?AT，?X∈P(U)，記：

則BelA，PlA:P(U)→[0,1]是U上一對對偶的信任函數與似然函數，其對應的mass函數為

2 不完備多粒度標記信息系統

在一個(完備)信息系統(U,AT)中，每一個對象xi在屬性aj上只取一個確定的值，這是單粒度標記信息系統.若信息系統(U,AT)中每一個對象在同一個屬性上，根據不同的粒度標記層面可以取不同的值，則(U,AT)是一個多粒度標記信息系統.Wu和Leung在文獻[24]中首次提出了多粒度標記信息系統的概念.

定義3[24]. 多粒度標記信息系統.稱(U,AT)是一個多粒度標記信息系統，其中U={x1,x2,…,xn}是一個非空有限對象集，稱為論域，AT={a1,a2,…,am}是一個非空有限屬性集，且每一個屬性都是多粒度屬性.假設所有的屬性都有I個相同的等級粒度，則一個多粒度標記信息系統可以表示為

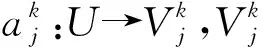
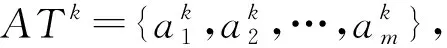
定義3中假設系統中的每一個屬性都有相同等級的粒度標記，但在實際生活中，各個屬性的粒度等級可能不一樣，針對這種情形，Li和Hu在文獻[34]中提出了一種基于不同屬性取不同等級粒度標記的多粒度標記信息系統，我們稱之為廣義多粒度標記信息系統.

定義4[34]. 廣義多粒度標記信息系統.稱(U,AT)是一個廣義多粒度標記信息系統，其中U={x1,x2,…,xn}是一個非空有限對象集，稱為論域，AT={a1,a2,…,am}是一個非空有限屬性集，且每一個屬性都是多粒度屬性.假設屬性aj有Ij個等級粒度標記，則一個多粒度標記信息系統可以表示為

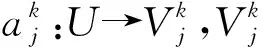
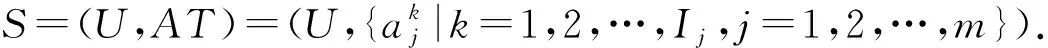
其中，k=1,2,…,Ij-1；j=1,2,…,m；x∈U.

可以驗證，(L,?)是一個偏序集，即?是L上的一個偏序關系(自反、傳遞和反對稱的關系).若進一步定義：

則(L,?,∧,∨)是一個有界格，顯然它是一個完備格，其中最小元是(1,1,…,1)，最大元是(I1,I2,…,Im)，并且：

K1?K2?K1∧K2=K1?K1∨K2=K2.

對于A?AT和K=(l1,l2,…,lm)∈L，記K在屬性子集A上的限制為KA，并記LA={KA|K∈L}，即LA是子多粒度標記信息系統(U,A)的粒度標記選擇全體.

對于A?AT和K=(l1,l2,…,lm)∈L，記：

RAK={(x,y)∈U×U|?al∈AKA,
al(x)=al(y)或al(x)=*或al(y)=*}，

則RAK是不完備多粒度標記信息系統S在粒度標記層面K=(l1,l2,…,lm)上由屬性集A導出的一個相似關系，特別地，對于a∈AT，記RaK=R{a}K.記：

SAK(x)={y∈U|(x,y)∈RAK}，x∈U.

SAK(x)稱為對象x關于AK的相似類.記：

URAK={SAK(x)|x∈U}.

定義6. 設U為非空集，A與B是U的2個覆蓋，若對于任意A∈A，存在B∈B使得A?B，則稱A比B細或B比A粗，記作AB.

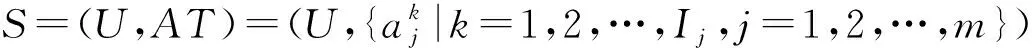
1)K1?K2?RAK1?RAK2；

2)K1?K2?SAK1(x)?SAK2(x),?x∈U；

3)K1?K2?URAK1URAK2；

4)A?B?AT?RBK?RAK,?K∈L；

證明. 直接驗證即得.

證畢.

對于X?U,K∈L，X關于RAK的下近似和上近似定義為

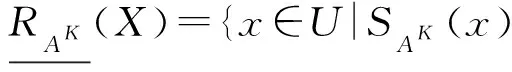
由定理2和上述下近似、上近似的定義容易得到如下：

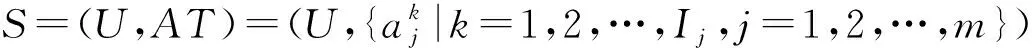
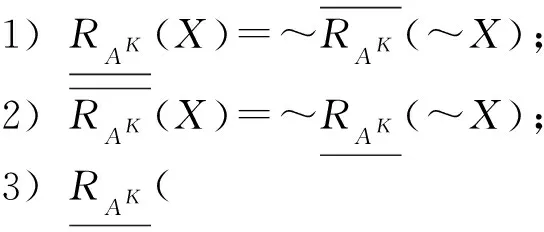
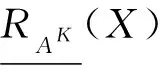
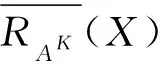
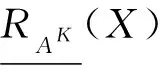
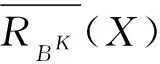
X關于RAK的近似精度定義為

X關于RAK的粗糙度定義為

ρAK(X)=1-αAK(X)，

則我們可以得到在不同的粒度標記層面下集合的近似精度與粗糙度的關系：

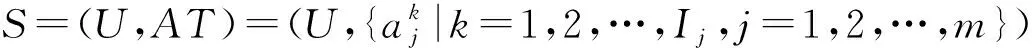
1)K1?K2?αAK2(X)≤αAK1(X)；

2)K1?K2?ρAK1(X)≤ρAK2(X).

定理4表明，粒度標記越小(細)，集合的近似精度越高而相應的粗糙度越小.

由定理1和定理3可得：

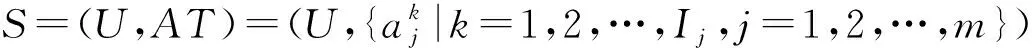
則BelAK，PlAK:P(U)→[0,1]是U上一對對偶的信任函數與似然函數，其對應的mass函數為

并且信任函數與似然函數滿足3個性質：

1) 對于K1，K2∈L，若K1?K2，則BelAK2(X)≤BelAK1(X)≤P(X)；

2) 對于K1，K2∈L，若K1?K2，則P(X)≤PlAK1(X)≤PlAK2(X)；

3) 若B?C?AT，則BelBK(X)≤BelCK(X)≤P(X)≤PlCK(X)≤PlBK(X).

3 不完備多粒度標記決策系統與最優粒度選擇

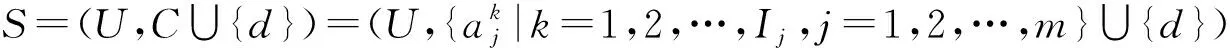
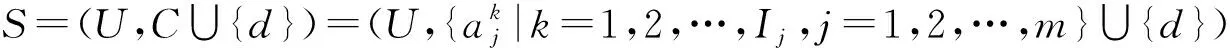
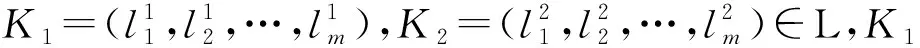
是協調的，即RCK2?Rd，則由定理2知，RCK1?RCK2?Rd，從而：

也是協調的，即在較粗的粒度標記層面下的不完備決策系統是協調的，則在較細的粒度標記層面下的不完備決策必定是協調的.

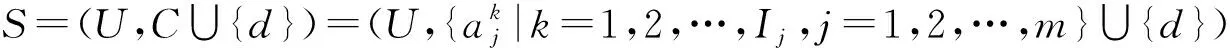
例1. 表1是一個不完備多粒度標記決策表S=(U,C∪g0gggggg)，其中U={x1,x2,…,x8}，C={a1,a2,a3}，其中“S”,“M”,“L”,“Y”,“N”分別表示“小”、“中等”、“大”、“是”、“否”等.屬性a1與a3有3個粒度層面的標記，屬性a2只有2個粒度層面的標記.

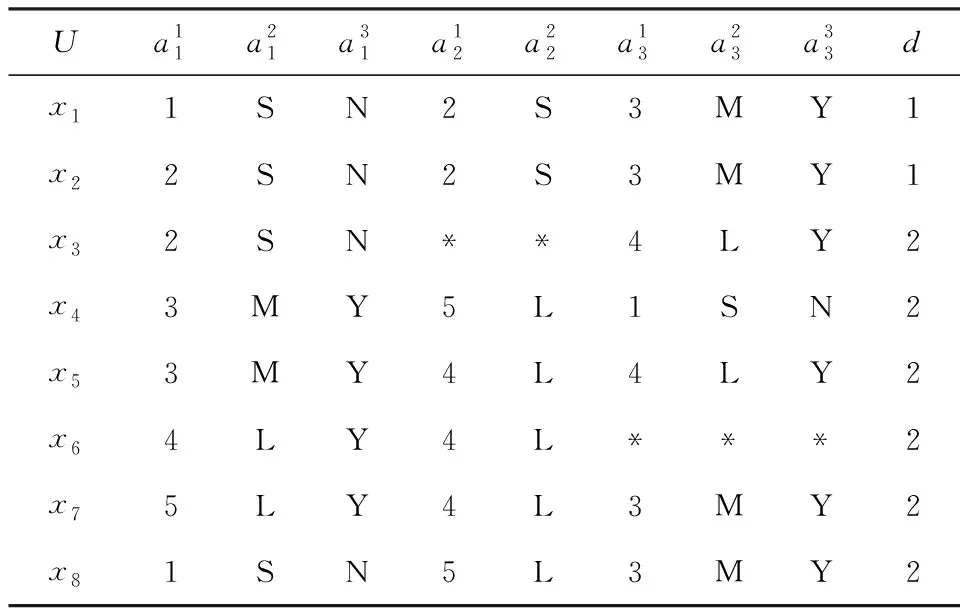
Table 1 An Incomplete Multi-Granular LabeledDecision System表1 一個不完備多粒度標記決策系統

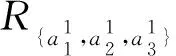
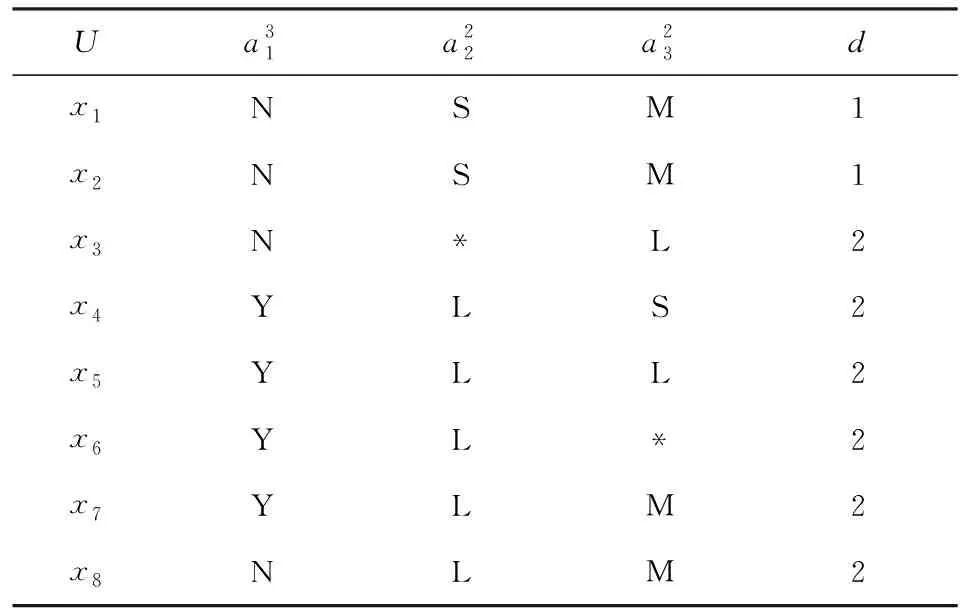
Table 2 The Incomplete Decision Table with the GranularLabel Selection K=(3,2,2)表2 對應于粒度標記選擇K=(3,2,2)的不完備決策表

我們下面討論用證據理論中的信任函數和似然函數來刻畫最優粒度標記選擇的特征.為了方便起見，不妨設Vd={1,2,…,r}，記Dj={x∈U|d(x)=j}，j∈{1,2,…,r}，URd={Dj|j=1,2,…,r}.

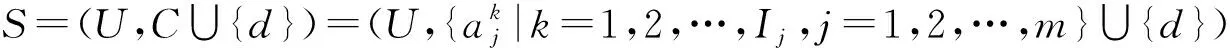
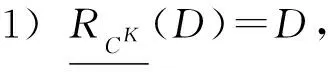
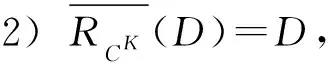
證明. 1) 對于任意D∈URd，由定理3知，?D.另一方面，對于任意x∈D，顯然[x]d={y∈U|d(y)=d(x)}=D.由于SK=(U,CK∪g0gggggg)是協調的，從而SCK(x)?[x]d=D，由下近似的定義知于是D?因此，

2) 對于任意D∈URd，由定理3知，D?另一方面，對于任意由上近似的定義知，SCK(x)∩D≠?.對于任意y∈SCK(x)∩D，顯然[y]d=D，又由于RCK是對稱的，從而由y∈SCK(x)可得x∈SCK(y).由于SK=(U,CK∪g0gggggg)是協調的，因此SCK(y)?[y]d，從而x∈SCK(y)?[y]d=D，于是?D，故

證畢.

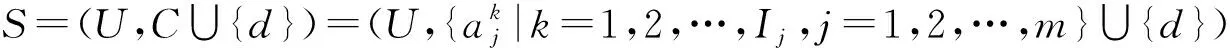
證明. “1)?2)”由于SK=(U,CK∪g0gggggg)是協調的，由定理6知，對于任意Di∈URd有從而因此，

(1)

由定理5知，對于任意Di∈URd有BelCK(Di)≤BelC1(Di)，因此由式(1)可得：

于是：

(2)

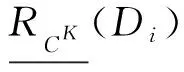
SCK(y)?[x]d，

(3)

由于x∈[x]d，在式(3)中取y=x即得SCK(x)?[x]d，因此RCK?Rd，即SK=(U,CK∪g0gggggg)是協調的.

“1)?3)”由于SK=(U,CK∪g0gggggg)是協調的，由定理6知，對于任意Di∈URd有從而因此，

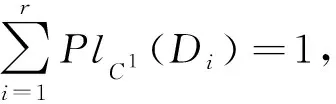
(4)

由定理5對于任意Di∈URd有PlC1(Di)≤PlCK(Di)，故由式(4)可得：

因此:

(5)

而由定理3知：

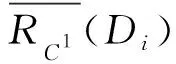
(6)

從而由式(5)和式(6)即得：

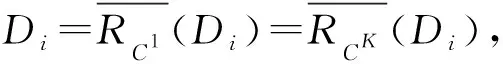
(7)

對于任意x∈U，取D∈URd使得x∈D，顯然[x]d=D.對于任意y∈SCK(x)，由于RCK是對稱的，因此x∈SCK(y)，從而SCK(y)∩[x]d≠?，于是由上近似定義可得故由式(7)知y∈[x]d，這樣我們證明了對于任意x∈U有SCK(x)?[x]d，即RCK?Rd，因此SK=(U,CK∪g0gggggg)是協調的.

證畢.

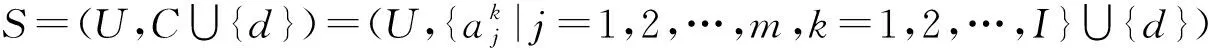
1) 粒度標記選擇K是最優的；

證畢.

例2. (續例1)在表1給出的例中，經計算當K=(3,2,2)∈L時，

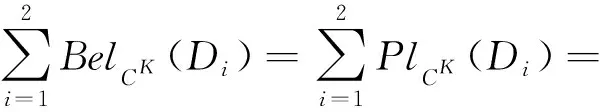
而對于H=(3,2,3)∈L,有:

又由于H=(3,2,3)是L中唯一嚴格粗于K的粒度標記選擇，由定理8可知K=(3,2,2)是S的最優粒度標記選擇.

4 結束語

本文介紹了廣義不完備多粒度標記信息系統的概念，在這種系統中不同屬性可以有不同的粒度標記層面個數.給出了在不同粒度標記層面下基本信息粒的表示及其相互關系，同時定義了基于相似關系的集合的下、上近似概念，并討論了近似算子的性質.引入了廣義不完備多粒度標記信息系統中的粒度標記選擇和廣義不完備多粒度標記決策系統中的最優粒度標記選擇的概念.并進一步用證據理論中的信任函數和似然函數刻畫了協調的不完備多粒度標記決策系統的最優粒度選擇的特征.由于廣義不完備多粒度標記決策系統中可能的粒度標記選擇的集合組合復雜度比較高，因此，尋求合適的算法求解最優粒度標記是一個值得研究的問題.對于一個不協調的不完備多粒度標記決策系統可以通過引入廣義決策函數，并用廣義決策函數代替原系統中的決策，可以將不協調的不完備多粒度標記決策系統轉化為協調的不完備多粒度標記決策系統，這樣就容易得到判別不協調的不完備多粒度標記決策系統中保持廣義決策不變的最優粒度選擇的特征.未來我們將研究不協調的不完備多粒度標記決策系統在其它各種意義下的最優粒度選擇問題和多粒度決策規則提取的方法.

[1]Zadeh L A. Fuzzy sets and information granularity[G]Advances in Fuzzy Set Theory and Applications. Amsterdam: North-Holland, 1979: 3-18

[2]Hobbs J R. Granularity[C]Proc of the 9th Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 1985: 432-435

[3]Zadeh L A. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy Sets and Systems, 1997, 90(2): 111-127

[4]Lin Tsau Young. Granular computing: From rough sets and neighborhood systems to information granulation and computing in words[COL]Proc of European Congress on Intelligent Techniques and Soft Computing, 1997 [2017-05-12]. http:xanadu.cs.sjsu.edu～drtylinpublicationspaperList101_34rsnsigcw3.pdf

[5]Lin Tsau Young. Granular computing: Structures, representations, and applications[G]LNAI 2639: Proc of the 9th Int Conf on Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. Berlin: Springer, 2003: 16-24

[6]Yao Yiyu. Granular computing: Basic issues and possible solutions[C]Proc of the 5th Joint Conf on Computing and Information. Durham: Duke University Press, 2000: 186-189

[7]Zhang Ling, Zhang Bo. Quotient Space Based Problem Solving: A Theoretical Foundation of Granular Computing[M]. Beijing: Tsinghua University Press, 2014 (in Chinese)(張鈴, 張鈸. 基于商空間的問題求解: 粒度計算的理論基礎[M]. 北京: 清華大學出版社, 2014)

[8]Duan Jie, Hu Qinghua, Zhang Lingjun, et al. Feature selection for multi-label classification based on neighborhood rough sets[J]. Journal of Computer Research and Development, 2015, 52(1): 56-65 (in Chinese)(段潔, 胡清華, 張靈均, 等. 基于鄰域粗糙集的多標記分類特征選擇算法[J]. 計算機研究與發展, 2015, 52(1): 56-65)

[9]Kryszkiewicz M. Rough set approach to incomplete information systems[J]. Information Sciences, 1998, 112(1-4): 39-49

[10]Leung Yee, Wu Weizhi, Zhang Wenxiu. Knowledge acquisition in incomplete information systems: A rough set approach[J]. European Journal of Operational Research, 2006, 168(1): 164-180

[11]Li Deyu, Zhang Bo, Leung Yee. On knowledge reduction in inconsistent decision information systems[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2004, 12(5): 651-672

[12]Lin Tsau Young, Yao Yiyu, Zadeh L A. Data Mining, Rough Sets and Granular Computing[M]. New York: Physica-Verlag, 2002

[13]Miao Duoqian, Wang Guoyin, Liu Qing, et al. Granular Computing: Past, Present and Future[M]. Beijing: Science Press, 2007 (in Chinese)(苗奪謙, 王國胤, 劉清, 等. 粒計算的過去、現在與展望[M]. 北京: 科學出版社, 2007)

[14]Miao Duoqian, Li Deyi, Yao Yiyu, et al. Uncertainty and Granular Computing[M]. Beijing: Science Press, 2011 (in Chinese)(苗奪謙, 李德毅, 姚一豫, 等. 不確定性與粒計算[M]. 北京: 科學出版社, 2011)

[15]Pedrycz W, Skowron A, Kreinovich V. Handbook of Granular Computing[M]. New York: Wiley, 2008

[16]Shao Mingwen, Zhang Wenxiu. Dominance relation and rules in an incomplete ordered information system[J]. International Journal of Intelligent Systems, 2005, 20(1): 13-27

[17]Shi Qianyu, Liang Jiye, Zhao Xingwang. A clustering ensemble algorithm for incomplete mixed data[J]. Journal of Computer Research and Development, 2016, 53(9): 1979-1989 (in Chinese)(史倩玉, 梁吉業, 趙興旺. 一種不完備混合數據集成聚類算法[J]. 計算機研究與發展, 2016, 53(9): 1979-1989)

[18]Sun Bingzhen, Ma Weimin, Gong Zengtai. Dominance-based rough set theory over interval-valued information systems[J]. Expert Systems, 2014, 31(2): 185-197

[19]Zhang Wei, Miao Duoqian, Gao Can, et al. A neighborhood rough sets-based co-training model for classification[J]. Journal of Computer Research and Development, 2014, 51(8): 1811-1820 (in Chinese)(張維, 苗奪謙, 高燦, 等. 鄰域粗糙協同分類模型[J]. 計算機研究與發展, 2014, 51(8): 1811-1820)

[20]Pawlak Z. Rough Sets: Theoretical Aspects of Reasoning about Data[M]. Amsterdam, Netherlands: Kluwer Academic Publishers, 1991

[21]Qian Yuhua, Liang Jiye, Yao Yiyu, et al. MGRS: A multi-granulation rough set[J]. Information Sciences, 2010, 180(6): 949-970

[22]Qian Yuhua, Liang Jiye, Dang Chuangyin. Incomplete multi-granulation rough set[J]. IEEE Trans on Systems, Man and Cybernetics, 2010, 40(2): 420-431

[23]Yang Xibei, Song Xiaoning, Chen Zehua. On multigranula-tion rough sets in incomplete information system[J]. International Journal of Machine Learning and Cybernetics, 2012, 3(3): 223-232

[24]Wu Weizhi, Leung Yee. Theory and applications of granular labeled partitions in multi-scale decision tables[J]. Information Sciences, 2011, 181(18): 3878-3897

[25]Wu Weizhi, Gao Cangjian, Li Tongjun. Ordered granular labeled structures and rough approximations[J]. Journal of Computer Research and Development, 2014, 51(12): 2623-2632 (in Chinese)(吳偉志, 高倉健, 李同軍. 序粒度標記結構及其粗糙近似[J]. 計算機研究與發展, 2014, 51(12): 2623-2632)

[26]Dai Zhicong, Wu Weizhi. Rough approximations in incomplete multi-granular ordered information systems[J]. Journal of Nanjing University: Natural Sciences, 2015, 51(2): 361-367 (in Chinese)(戴志聰, 吳偉志. 不完備多粒度序信息系統的粗糙近似[J]. 南京大學學報: 自然科學版, 2015, 51(2): 361-367)

[27]Wu Weizhi, Leung Yee. Optimal scale selection for multi-scale decision tables[J]. International Journal of Appro-ximate Reasoning, 2013, 54(8): 1107-1129

[28]Wu Weizhi, Chen Ying, Xu Youhong, et al. Optimal granularity selections in consistent incomplete multi-granular labeled decision systems[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(2): 108-115 (in Chinese)(吳偉志, 陳穎, 徐優紅, 等. 協調的不完備多粒度標記決策系統的最優粒度選擇[J]. 模式識別與人工智能, 2016, 29(2): 108-115)

[29]Wu Weizhi, Chen Chaojun, Li Tongjun, et al. A comparative study on optimal granularities in inconsistent multi-granular labeled decision systems[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(12): 1103-1111 (in Chinese)(吳偉志, 陳超君, 李同軍, 等. 不協調多粒度標記決策系統最優粒度的對比[J]. 模式識別與人工智能, 2016, 29(12): 1103-1111)

[30]She Yanhong, Li Jinhai, Yang Hailong. A local approach to rule induction in multi-scale decision tables[J]. Knowledge-Based Systems, 2015, 89: 398-410

[31]Gu Shenming, Wu Weizhi. On knowledge acquisition in multi-scale decision systems[J]. International Journal of Machine Learning and Cybernetics, 2013, 4(5): 477-486

[32]Gu Shenming, Wu Weizhi. Knowledge acquisition in inconsistent multi-scale decision systems[G]LNAI 6964: Proc of the 6th Int Conf on Rough Sets and Knowledge Technology. Berlin: Springer, 2011: 669-678

[33]Wu Weizhi, Qian Yuhua, Li Tongjun, et al. On rule acquisition in incomplete multi-scale decision tables[J]. Information Sciences, 2017, 378: 282-302

[34]Li Feng, Hu Baoqing. A new approach of optimal scale selection to multi-scale decision tables[J]. Information Sciences, 2017, 381: 193-208

[35]Wu Weizhi. Attribute reduction based on evidence theory in incomplete decision systems[J]. Information Sciences, 2008, 178(5): 1355-1371

WuWeizhi, born in 1964. Professor and PhD supervisor. Senior member of CCF. His main research interests include rough set theory, granular computing, random set theory, concept lattice, approximate reasoning, etc.

YangLi, born in 1994. Master. Her main research interests include rough set theory and granular computing (1214774932@qq.com).

TanAnhui, born in 1986. PhD. Lecturer. His main research interests include rough set theory, granular computing, artificial intelligence, etc (tananhui86@163.com).

XuYouhong, born in 1969. Associate professor. Her main research interests include rough set theory and granular computing (xyh@zjou.edu.cn).