GPS廣播星歷軌道誤差分布模型探討
劉瑞寧,李建文,郭亮亮,劉德智
(1.信息工程大學/北斗導航應用技術河南省協同創新中心,鄭州 450001;2.貴州省水利水電勘測設計研究院,貴陽 550000)
0 引言
隨著全球衛星導航系統(global navigation satellite system,GNSS)的迅速發展,導航定位技術在諸多科研和生產領域得到了廣泛的應用;人們對導航系統性能的要求越來越嚴格:開展對導航系統服務性能的監測評估研究十分必要。文獻[1]詳細給出了監測評估的主要研究內容與方法,并提出了一種基于衛星軌道長期演化特點來確定監測范圍的方法。文獻[2]對星歷誤差進行了評估并分析了相關評估手段,通過實測GNSS數據,對目前四大系統的廣播星歷進行了評估與數據分析。目前已有大量文獻對廣播星歷精度評估展開研究,但關于廣播星歷的軌道誤差分布模型的研究相對較少[3-5],而軌道誤差分布模型的確定是開展GNSS導航電文的實時監測的基礎和前提。
本文提出一種利用精密星歷來計算廣播星歷軌道誤差的算法,并對軌道誤差的分布模型進行假設檢驗,最終確定軌道誤差所服從的分布模型。
1 基本計算模型
1.1 廣播星歷
全球定位系統(global positioning system,GPS)廣播星歷中包含了6個軌道根數及9個攝動參數和其他參數,而利用廣播星歷計算瞬時歷元t時刻的衛星位置的具體方法也在眾多文獻中有所介紹[6-7]。
1.2 精密星歷
國際GNSS服務組織(International GNSS Service,IGS)精密星歷給出的衛星的位置精度優于5 cm,相對于廣播星歷而言,事后精密星歷可以視作真值。當要計算其他時刻的鐘差與衛星坐標時,可以采用內插的方法。而關于精密星歷擬合軌道的插值方法,已有學者進行過研究比較,常見的是拉格朗日多項式插值法[8-9]。
1.3 軌道誤差計算模型
據前所述,可求得由廣播星歷計算得出的實時軌道位置和由精密星歷擬合的真實的軌道位置,從而可求出軌道誤差,其表達式為
(VX,VY,VZ)T=(X1,Y1,Z1)T-(X2,Y2,Z2)T
(1)
式中:(X1,Y1,Z1)T為由精密星歷擬合的真實的衛星軌道3維位置;(X2,Y2,Z2)T為由廣播星歷計算得出的實時衛星軌道3維位置;(VX,VY,VZ)T為軌道X、Y和Z方向誤差。值得注意是在計算軌道誤差時,參考框架、衛星相位中心與時空基準應相一致,否則將直接影響軌道誤差值的正確與否[10]。
2 誤差分布模型檢驗
2.1 常見假設檢驗
1)χ2擬合檢驗法。χ2(即卡方)擬合檢驗就是統計樣本的實際觀測值與理論推斷值之間的差異,觀測值與理論值之間的差異與卡方值是正相關的,差異越小卡方值越小,反之卡方值越大;如果觀測值與理論值完全相等時,卡方值為0,表明觀測值與理論值完全符合。其詳細檢驗步驟見其他文獻[11],[12]146-151。
2)偏度和峰度聯合檢驗法。由于正態分布的密度曲線是對稱且陡緩適中的,可以用偏度和峰度2個數字特征來描述分布密度曲線;其中偏度指密度曲線的偏斜程度,峰度描述的是密度曲線的陡緩程度。若樣本來自正態總體,則其經驗分布密度曲線既不能偏斜太多又不能陡緩過度;因為對于正態分布而言,偏度為0,峰度為3:因此當樣本來自正態總體時,其偏度應接近于0,峰度接近于3[12]158-160。
3)正態概率紙檢驗法。正態概率紙檢驗法的基本思路是把正態分布的分布函數轉化為概率紙上的線性函數,其過程詳見相關文獻[12]160-163,[13]。
2.2 實驗分析與模型確定
本文實驗采用國際GNSS監測與評估系統(international GNSS monitoring and assessment system,iGMAS)分析中心接收的廣播星歷及IGS事后精密星歷,選取2016-01-01 T 00:00到2017-08-24 T 00:00時間段的數據,依據廣播星歷更新時間,2 h采集1個樣本數據。根據第1節中的計算思路可得出檢驗量即廣播星歷軌道誤差,進而對這些誤差樣本進行統計分析與假設檢驗。
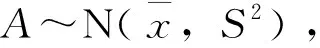
假設檢驗工具是采用Matlab中所含的檢驗函數,主要檢驗函數為正態分布Jarque-Bera檢驗函數jbtest即偏度與峰度的聯合檢驗、chi2gof檢驗函數即卡方擬合優度檢驗、Kolmogorov-Smirnov檢驗函數kstest、正態分布概率紙檢驗normplot。其中第4種屬于繪圖檢驗。
按照衛星的類型(IIF、IIR、IIR-M)分別選取G03、G07、G12、G18、G19、G24 6顆衛星作為例證數據來進行檢驗。其中G03和G24為IIF型衛星,G18和G19為IIR型衛星,G07和G12為IIR-M型衛星。
經過實驗分析對樣本數據進行統計,得出基本的特征數字如表1所示。
表1中VX、VY和VZ分別表示軌道X方向誤差、Y方向誤差和Z方向誤差。從表1中可以看出,軌道誤差的均方根(root mean square,RMS)均在合理范圍以內[14]。
根據軌道誤差數據的基本特征,采用均值和標準差作為參數進行分布擬合的檢驗,即檢驗是否服從正態分布和T分布。檢驗結果如表2所示。
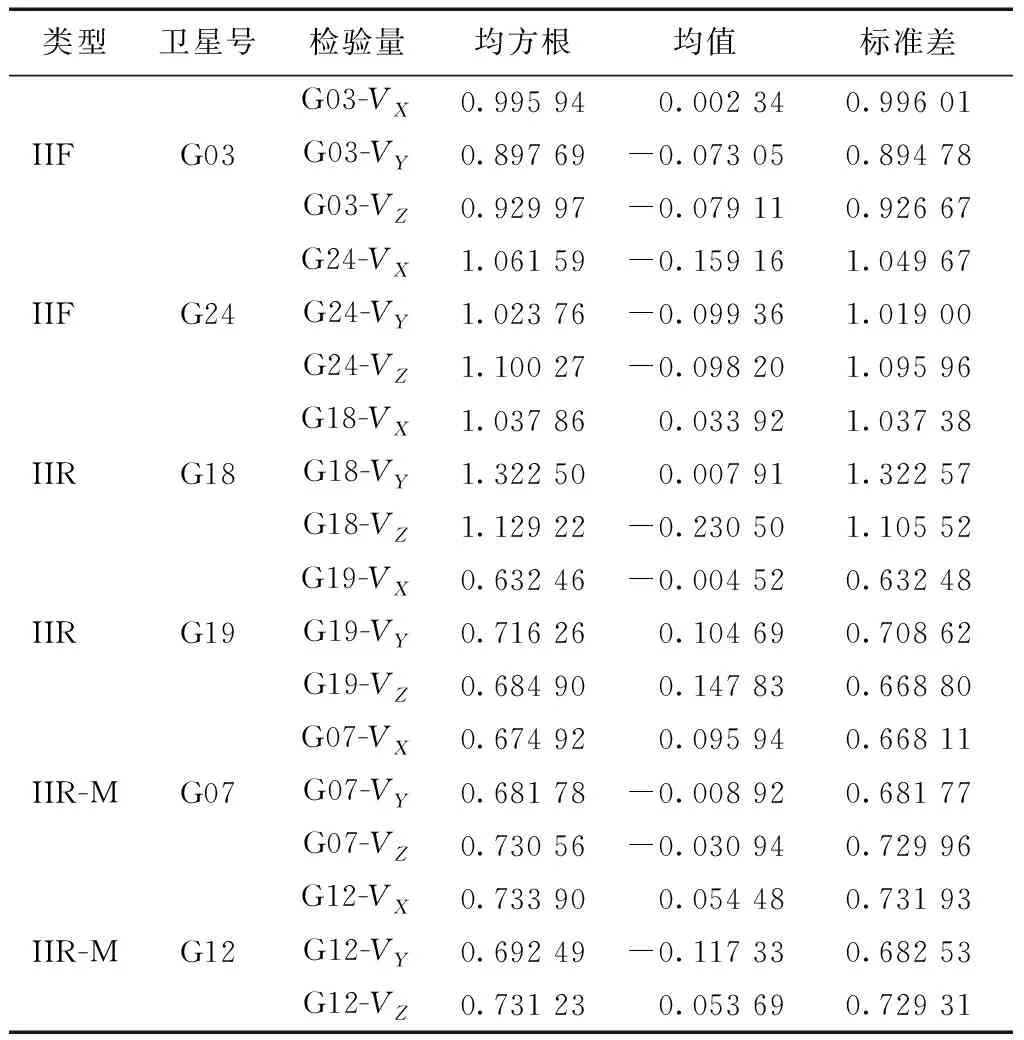
表1 軌道的誤差統計信息 m
表2中“0”表示肯定,即樣本服從假定分布;“1”表示否定,即樣本不服從假定分布。從表中可以看出:誤差樣本不服從T分布;而且大部分樣本也不服從正態分布,只有個別樣本服從正態分布。
本文還對所有樣本進行了直方統計和正態概率紙檢驗,這樣不僅可以有另一種結果作為輔助判斷,更能直觀顯示數據的分布形態。檢驗結果見圖1~圖6,每一幅大圖中有6幅小圖,其中圖(a)、圖(b)、圖(c)分別為軌道X、Y和Z方向誤差的直方統計,圖(d)、圖(e)、圖(f)分別為軌道X方向、Y方向和Z方向誤差的正態概率紙檢驗。直方統計圖中:橫坐標為樣本值;縱軸為頻次,即在該區間段樣本出現的次數;
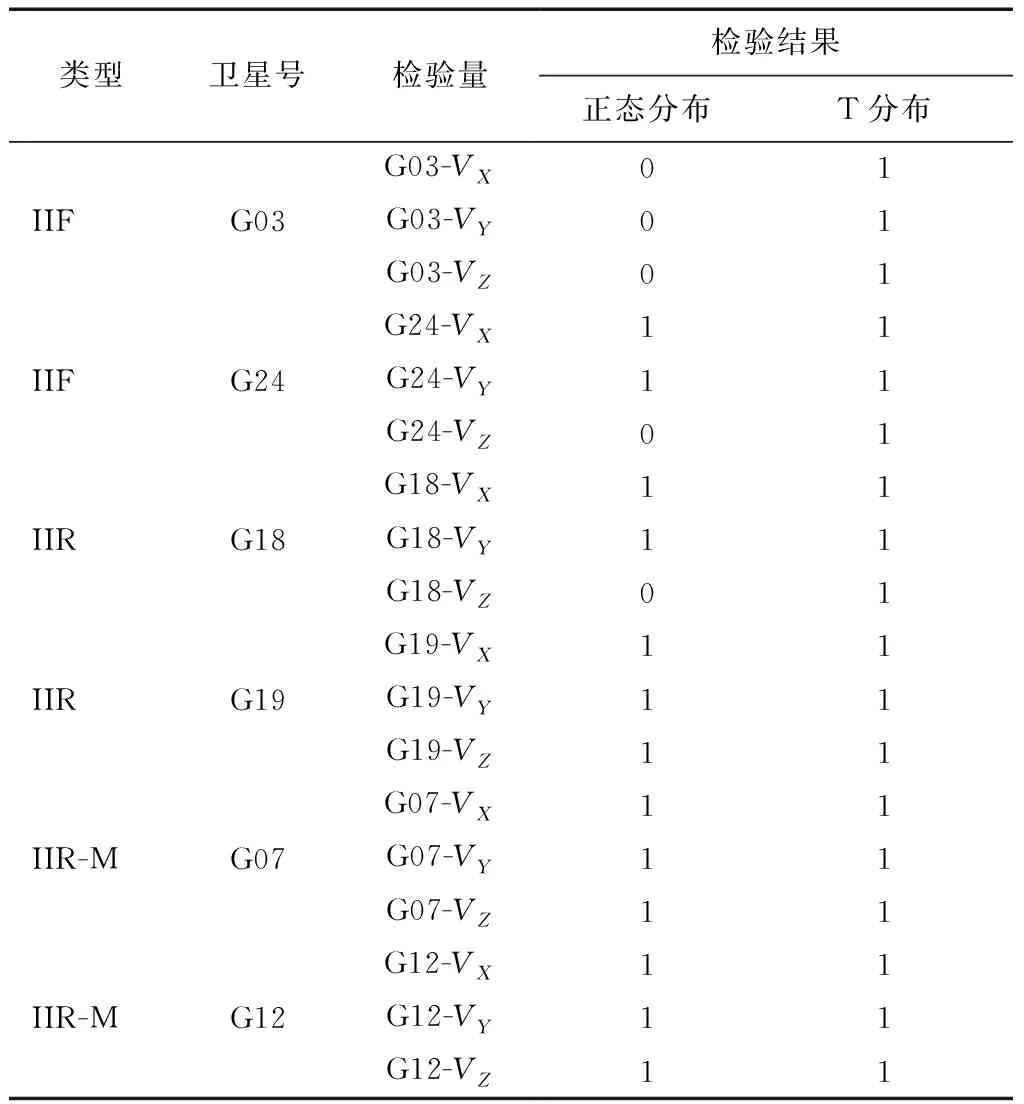
表2 軌道誤差檢驗結果
擬合曲線為適應該樣本數據的正態分布曲線。正態紙檢驗圖中:橫坐標表示樣本值,縱坐標表示百分位數,直線為參照線,星形點為數據點;當樣本數據服從正態分布時,樣本值所對應的百分位數就會越來越靠近參照線從而形成一條近似的直線,否則就會越來越偏離漸近線形成曲線。
從圖中可知:G03、G07、G12、G19、G24軌道誤差最近似服從正態分布,而G18(圖5)的軌道誤差分布呈明顯的雙峰特征。而當直方圖出現雙峰特征時,可以推斷是由于樣本值來自2個總體、2個分布的數據混合。
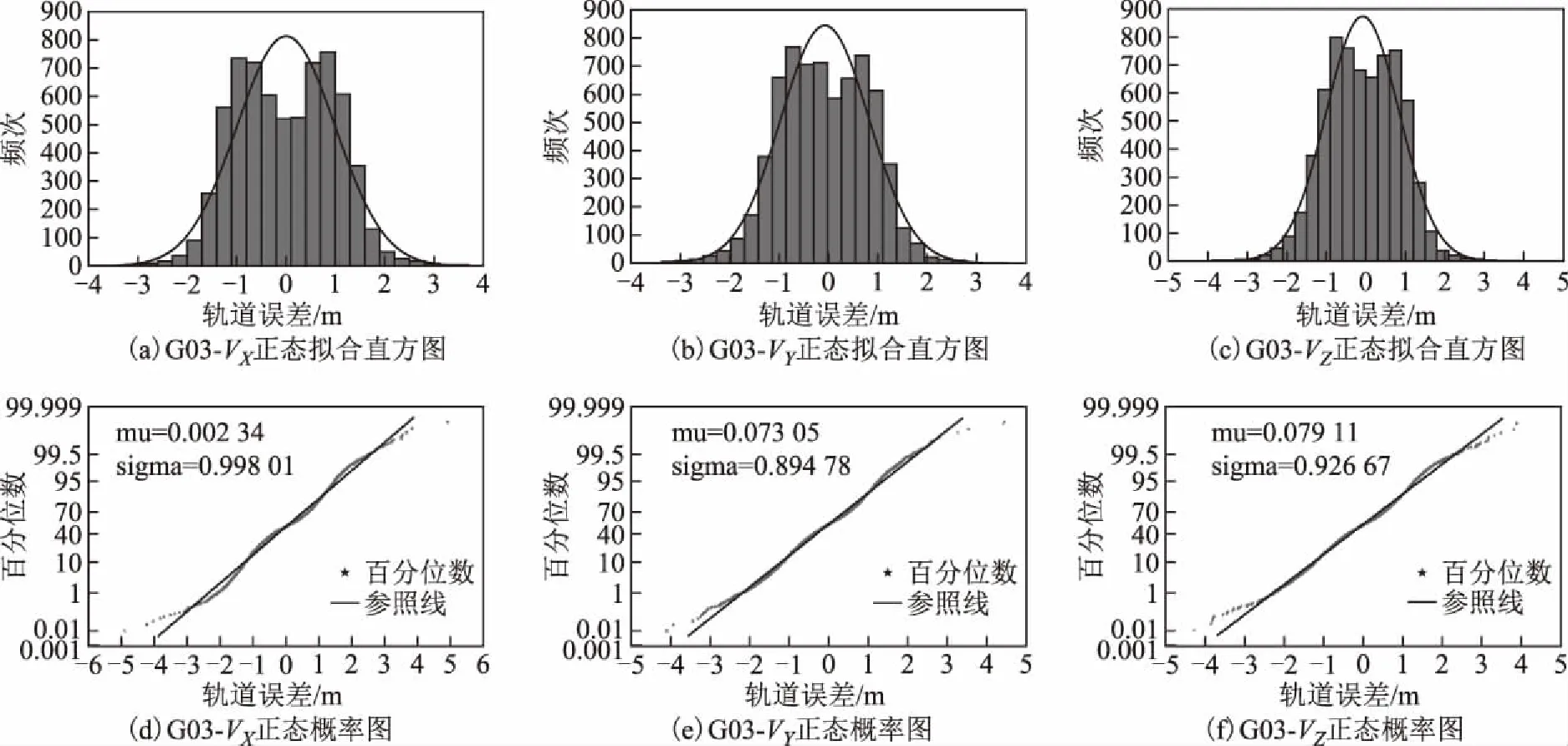
圖1 G03軌道誤差直方統計與正態概率紙檢驗
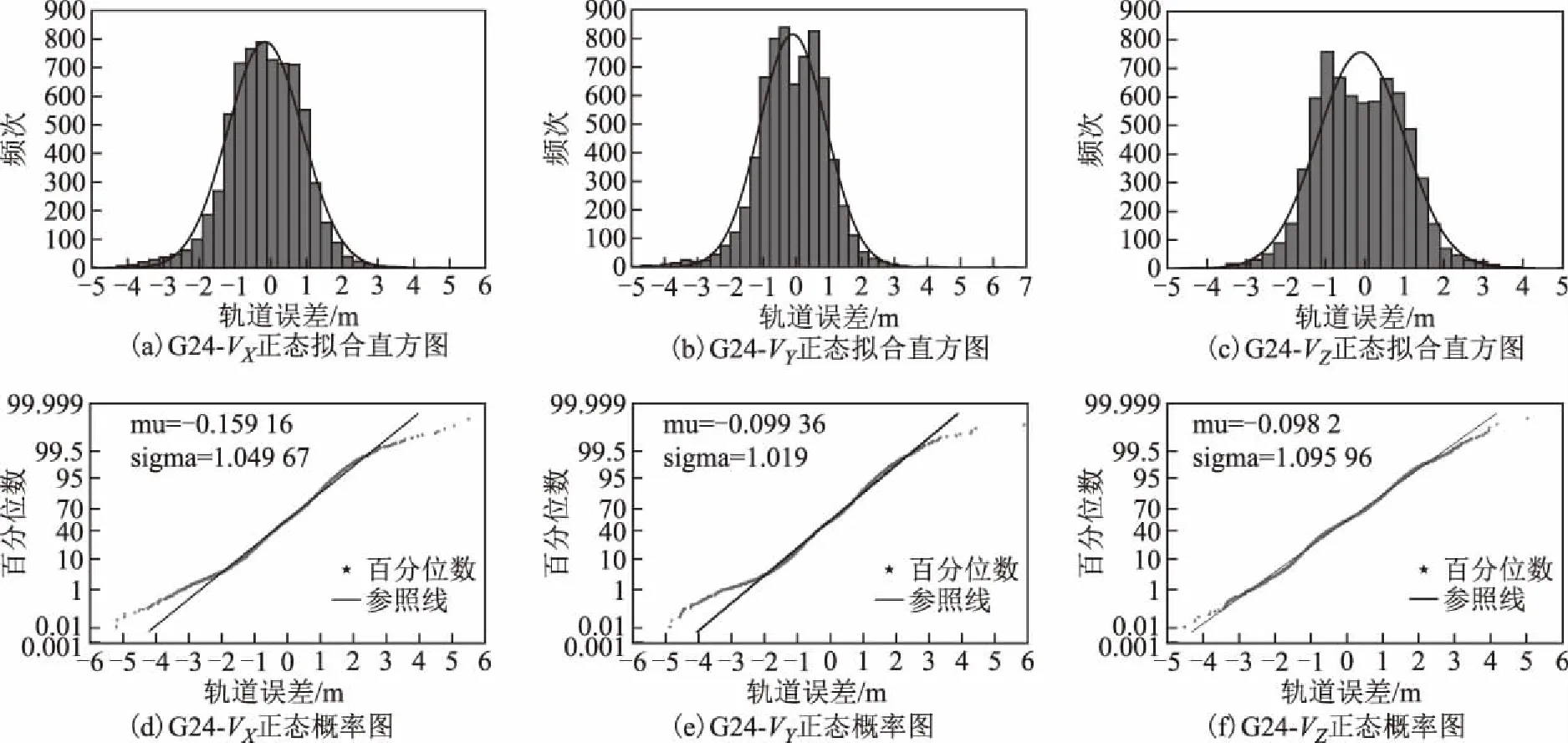
圖2 G24軌道誤差直方統計與正態概率紙檢驗
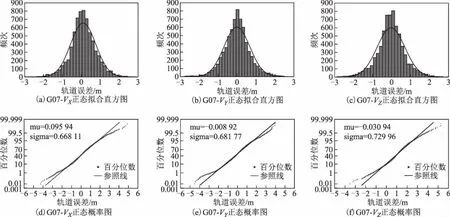
圖3 G07軌道誤差直方統計與正態概率紙檢驗
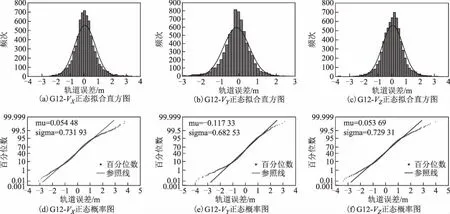
圖4 G12軌道誤差直方統計與正態概率紙檢驗

圖5 G18軌道誤差直方統計與正態概率紙檢驗
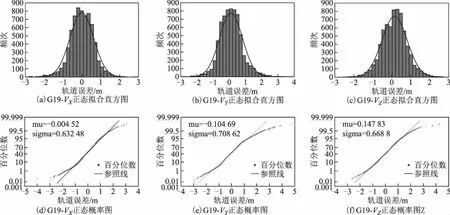
圖6 G19軌道誤差直方統計與正態概率紙檢驗
2.3 具有雙峰特征的誤差分布檢驗
對于具有雙峰特征的G18的軌道誤差,根據雙峰分布的基本理論對軌道誤差呈現雙峰分布特征的數據進行分段擬合檢驗,分別對2段樣本數據進行正態分布、T分布以及Weibull分布檢驗。根據軌道誤差數據的基本特征,均值取值都在0附近,所以取分界值為0。其中Weibull分布檢驗只檢驗樣本值大于0時的樣本總體;這是因為Weibull分布的變量取值區間需在[0,+),檢驗所需的形狀參數和比例參數根據樣本值進行擬合。而兩側的樣本分布在總的雙峰分布中所占的比重也由兩側數據量所占的比值決定[15-16]。
重復2.2節檢驗過程,得出結果如表3和圖7~圖9所示。從結果可知,正負兩側的數據均近似服從正態分布,據此可以推斷出G18軌道誤差最近似服從的分布是由2個正態分布組成的雙峰分布。
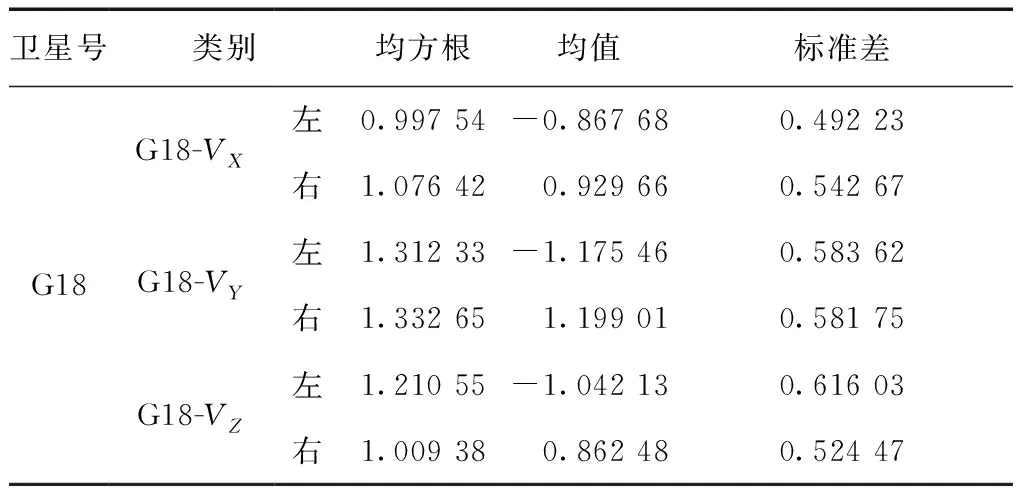
表3 具有雙峰分布特征的軌道的誤差統計 m

圖7 G18軌道X方向誤差直方統計與正態概率紙檢驗
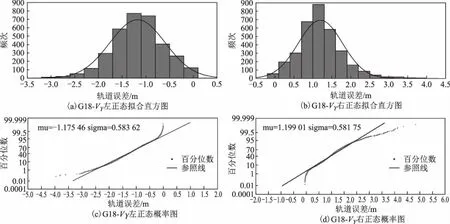
圖8 G18軌道Y方向誤差直方統計與正態概率紙檢驗

圖9 G18軌道Z方向誤差直方統計與正態概率紙檢驗
另外,除了以上例證的衛星,本文還檢驗了所有其他的GPS在軌衛星,發現除了G18的軌道誤差具有雙峰分布特征外,G11、G13、G14、G18、G20、G28的軌道誤差具有同樣的分布特征,而這些衛星均為IIR星。
3 結束語
監測評估工作是評價和確保衛星導航系統服務性能的有效手段。本文主要分析了以精密星歷為基準的GPS廣播星歷的軌道誤差,并對這些誤差進行擬合分布檢驗。從分析結果來看,衛星的軌道誤差(X、Y、Z方向)出現了多樣性:其中IIF星和IIR-M星及個別IIR星的誤差分布模型最近似服從以均值和標準差為參數的正態分布;大部分IIR星的誤差分布模型呈現雙峰特征,且是服從由2個正態分布混合而成的雙峰分布。當軌道誤差呈雙峰分布時,如何更精準地對廣播星歷進行監測與評估是下一步的研究工作。
致謝:感謝iGMAS信息工程大學分析中心(LSN)給予的幫助和支持。
[1] 張清華.GNSS監測評估理論與方法研究[D].鄭州:信息工程大學,2014.
[2] 劉帥.衛星導航系統空間信號精度評估理論與算法研究[D].鄭州:信息工程大學,2016.
[3] 張耀文.GPS廣播星歷及其精度評估研究[D].西安:長安大學,2007.
[4] 陳永就.GNSS廣播星歷的精度評定[J].測繪與空間地理信息,2015,38(6):186-191.
[5] MONTENBRUCK O,STEIGENBERGER P,HAUSCHILD A.Broadcast versus precise ephemerides:a multi-GNSS perspective[J].GPS Solutions,2015,19(2):321-333.
[6] 劉磊,盛崢,王迎強,等.利用廣播星歷計算GPS衛星位置及誤差分析[J].理工大學學報(自然科學版),2006,7(6):592-596.
[7] 王俊杰,許杭,高俊強.基于廣播星歷改正實時精密星歷與鐘差獲取研究[J].全球定位系統,2015,40(5):21-25.
[8] 張養安,李俊鋒,薛兆元,等.IGS精密星歷和鐘差的算法比較研究[J].地理信息世界,2016,23(4):45-49.
[9] 吳繼忠,高俊強,李明峰.IGS精密星歷和鐘差插值方法的研究[J].工程勘察,2009,37(7):52-54.
[10] 郭斐,張小紅,李星星,等.GPS系列衛星廣播星歷軌道和鐘的精度分析[J].武漢大學學報(信息科學版),2009,34(5):589-592.
[11] 沈宏峰,陳群.實用的卡方檢驗法[J].微型電腦應用,1997(5):61-63.
[12] 莊楚強,何春雄.應用數理統計基礎[M].3版.廣州:華南理工大學出版社,2006.
[13] 岳鵬,朱坤平.基于隨機模擬方法對正態概率紙檢驗的改進[J].統計與決策,2017(3):14-16.
[14] 王霞迎,秘金鐘,張德成,等.GPS廣播星歷位置、速度和鐘差精度分析[J].大地測量與地球動力學,2014,34(3):164-168.
[15] 徐鑫,郭民之,石峰利.雙峰數據分布的模擬[J].云南師范大學學報,2013,33(2):46-51.
[16] 馮祖德,涂銘旌,鄢文彬.韌性值呈雙峰分布時參數的統計推斷問題的探討[J].理化檢驗:物理分冊,1992,28(5):30-32.

