纖維增強復合薄殼固有特性計算及驗證

周正學 李 暉 薛鵬程 吳懷帥 陳姝瑤

1.東北大學機械工程與自動化學院，沈陽，110819 2.東北大學理學院，沈陽，110819

0 引言

纖維增強復合薄殼相對于金屬薄殼，具有質(zhì)量小、耐腐蝕、絕緣性好等特點，被越來越多地應用于航空航天、船舶、海洋工程、石油化工、兵器制造以及核工業(yè)等重要領域［1］。纖維增強復合薄殼通常處于一端約束的懸臂邊界條件下，如航空發(fā)動機的機匣、復合鼓筒、復合雷達罩等［2］。復合薄殼的振動問題突出，容易產(chǎn)生共振、疲勞和損傷等故障［3-6］。對懸臂邊界下的纖維增強復合薄殼固有特性進行理論及實驗驗證的研究還不夠完善，因此，研究懸臂邊界下纖維增強復合薄殼的振動特性問題有著重要的工程及學術(shù)意義［7］。

固有特性是深入研究結(jié)構(gòu)系統(tǒng)振動特性的基礎，對理論分析、動態(tài)設計、故障診斷都有著重要的指導作用。長期以來，國內(nèi)外學者在研究纖維增強復合材料薄殼的固有特性方面做了很多的工作，已經(jīng)取得了階段性的研究成果。AZARAFZA等［8］基于Love殼體理論，采用一階剪切變形理論分析了簡支邊界下復合薄壁圓柱殼的固有特性問題。LI等［9］采用傳遞矩陣以及有限元法求解了懸臂狀態(tài)下金屬薄壁圓柱殼的固有特性問題，并通過實驗測試對理論方法進行了驗證。RIBEIRO［10］將薄殼理論和一階剪切變形理論計算獲得的固有頻率，與有限元方法獲得的結(jié)果進行了對比，結(jié)果表明一階剪切變形理論的計算結(jié)果更加準確。HASHEMIAN等［11］通過理論解析的方法計算獲得了復合實心薄圓柱殼和復合網(wǎng)狀薄圓柱殼的固有頻率，并采用有限元法對理論解析結(jié)果進行了驗證，最后發(fā)現(xiàn)，尺寸及物理參數(shù)相同時，網(wǎng)殼的固有頻率小于實心殼的固有頻率。CHEN等［12］利用Navier-Stokes理論和Flügge薄殼理論，對帶有阻尼層的復合薄殼的固有頻率影響因素進行了分析，研究表明復合薄殼固有頻率隨涂層密度的增大而減小，隨涂層彈性模量的增大而增大。宋旭圓［13］采用Rayleigh-Ritz法研究了簡支邊界條件下纖維增強復合薄殼的固有特性問題，發(fā)現(xiàn)纖維鋪設角度的變化對復合殼體振動特性的影響呈明顯的周期性。項爽［14］通過數(shù)值積分方法，分析了簡支-簡支、自由-簡支兩種邊界條件下纖維增強復合薄殼的固有特性問題，發(fā)現(xiàn)隨著厚徑比的增大，簡支-簡支邊界條件下復合薄殼的固有頻率逐漸增大，而自由-簡支邊界條件下復合薄殼的固有頻率卻逐漸減小。李學斌［15］采用分離變量法和Flügge經(jīng)典殼體理論，計算了正交各向異性圓柱殼在懸臂邊界條件下的固有頻率和模態(tài)振型，但僅獲得了量綱一固有頻率。戴亦俊［16］采用Donnell簡化殼體理論，通過配點法計算了含有液體的復合薄殼的固有頻率和模態(tài)振型，并將其與實驗求得的頻率進行比較，結(jié)果表明，復合殼內(nèi)液體會使圓柱殼的固有頻率下降，且含水量越大，其各階固有頻率越低。樓玲娜［17］利用Donnell殼體理論得出殼體振動方程，并研究了纖維增強復合薄殼在懸臂邊界條件下的固有特性，但沒有將計算結(jié)果與其他相關(guān)論文或?qū)嶒炦M行對比驗證。

雖然人們已對纖維增強復合薄殼的固有特性進行了深入研究，但上述研究工作絕大部分針對理想的邊界條件，在懸臂狀態(tài)下通過理論與實驗相結(jié)合的方法對其固有特性進行研究的較少，且絕大多數(shù)文獻得出的頻率多為量綱一頻率，并未得到實驗數(shù)據(jù)驗證。為此，有必要繼續(xù)研究懸臂邊界下該類型復合材料結(jié)構(gòu)的固有特性。

本文對懸臂狀態(tài)下纖維增強復合薄殼的固有頻率和模態(tài)振型進行了計算及實驗驗證。在考慮纖維增強復合材料纖維方向影響的前提下，對纖維增強復合薄殼進行了理論建模，并采用正交多項式法來表示復合薄殼的振型函數(shù)，隨后通過Ritz法對該類型復合薄殼的固有頻率進行了求解。將計算獲得的某階固有頻率對應的特征向量回代入振型函數(shù) u(x,θ,t)、v(x,θ,t)和 w(x,θ,t)中，即可獲得復合薄殼結(jié)構(gòu)的某階模態(tài)振型，重復以上步驟可獲得復合薄殼的各階固有頻率。

1 固有特性理論計算

1.1 理論建模

所研究的纖維增強復合薄殼是由N層具有正交各向異性的纖維和基體材料組合而成的（圖1）。首先，將復合薄殼的中面作為參考平面，建立XθZ坐標系。纖維方向與整體坐標系 X軸方向的夾角為 β，殼體長為 L，中面半徑為R，殼體厚度為h，每一層位于Z坐標軸較低表面hk-1和較高表面hk之間，每層的厚度均相同。圖1中，1代表纖維縱向，2代表纖維橫向。假設纖維增強復合薄殼平行纖維方向的彈性模量為E1，垂直纖維方向的彈性模量為E2，1-2平面內(nèi)的剪切彈性模量為G12，1方向作用應力引起1、2方向應變的泊松比為 μ1，2方向作用應力引起1、2方向應變的泊松比為 μ2。

圖1 纖維增強復合薄殼理論模型Fig.1 The theoretical model of FRCS

根據(jù)板殼振動理論，將位移場寫為

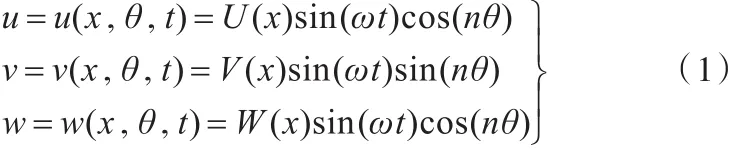
其中，u、v、w分別為殼內(nèi)任意一點在 X、θ、Z三個方向的坐標位置；n為圓柱殼的周向波數(shù)；ω為復合材料層圓柱殼的固有圓頻率；U(x)為 X方向的振型函數(shù)；V(x)為θ方向的振型函數(shù)；W(x)為Z方向的振型函數(shù)。

對于正交各向異性材料，平面應力狀態(tài)主方向有下列關(guān)系：

當材料主軸與整體坐標系之間有一定夾角β時，用應力-應變轉(zhuǎn)軸公式計算得到第k層殼體在整體坐標系下的應力-應變關(guān)系為

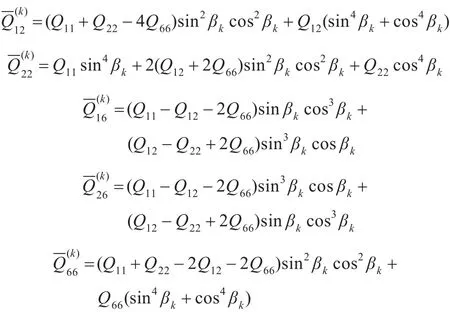
式中，βk為第k層薄殼的纖維方向與整體坐標系X軸的夾角。

薄殼振動的動能

其中，ρ為纖維增強復合薄殼的密度。

彈性體因受力變形而在結(jié)構(gòu)內(nèi)部產(chǎn)生應變和應力，所以使結(jié)構(gòu)內(nèi)部產(chǎn)生了變形勢能。根據(jù)板殼振動理論假設，薄壁圓柱殼的應變能EU為

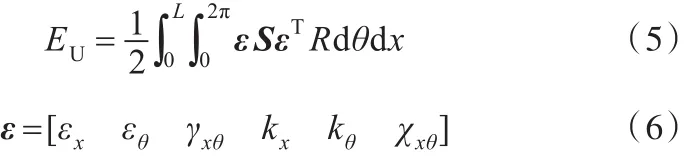
根據(jù)Love殼體理論，可得

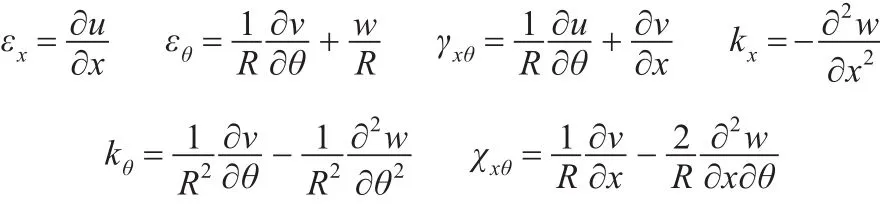
纖維增強復合薄殼結(jié)構(gòu)的薄膜剛度矩陣為

其中，第k層的較高表面、較低表面到參考平面的距離分別為Hk與 Hk-1。

將位移公式（式（1））和應力公式（式（3））代入式（4）、式（5），可以得到復合薄殼的動能和應變能：

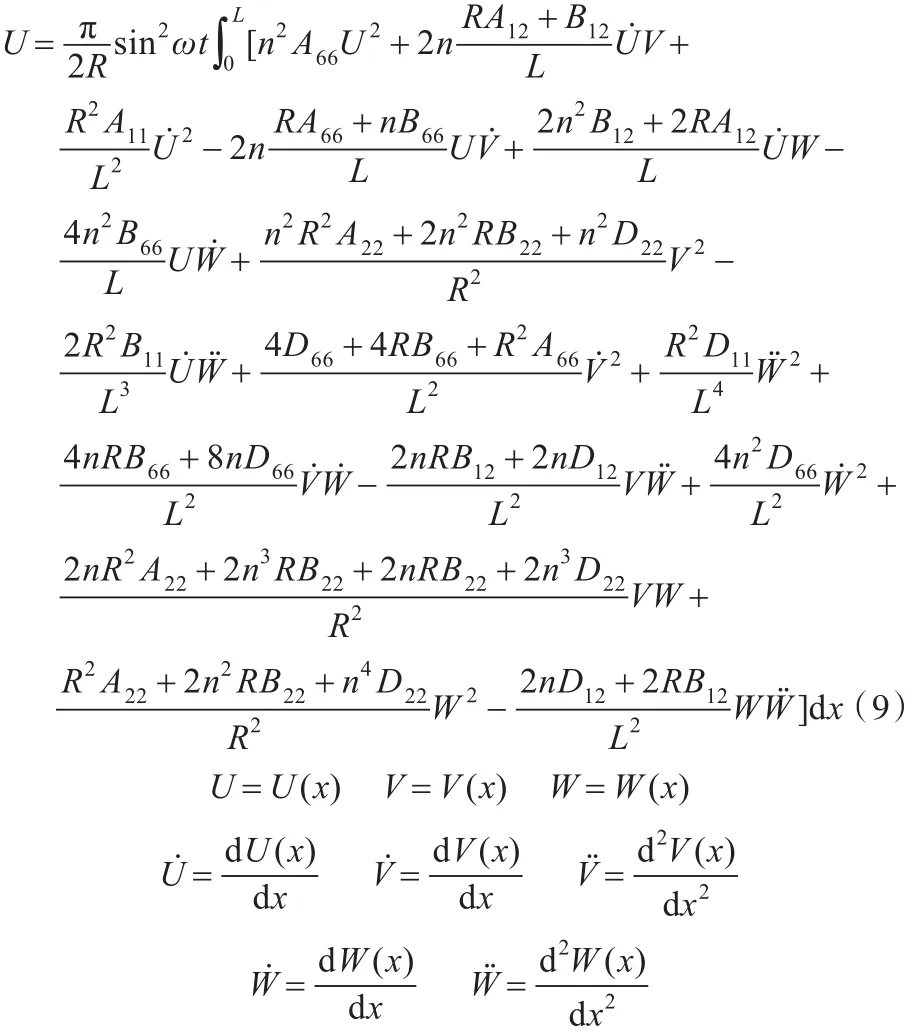
1.2 Ritz法求解

由于解析法很難得到懸臂薄殼的精確解，故本文采用Ritz近似解法。根據(jù)Ritz法，中面位移為

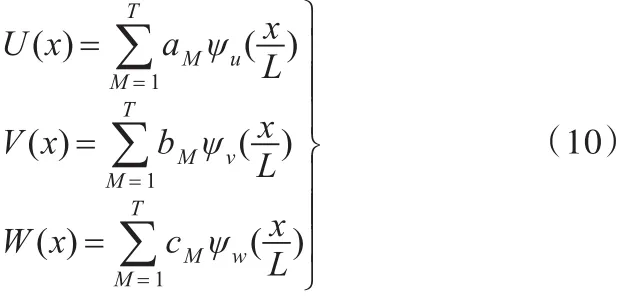
其中，aM、bM、cM為系數(shù)；ψu(ξ)、ψv(ξ)、ψw(ξ)是滿足幾何邊界條件與力學邊界條件正交的Schmidt函數(shù)，ξ=x/L；T為通過Ritz法截取的項數(shù)。

本文通過對滿足懸臂邊界條件的多項式函數(shù)進行正交化處理，來獲得一系列的正交多項式：

將式（10）代入式（8）、式（9），得到用待定參數(shù)aM、bM、cM表示的應變能和動能表達式，即可得到最大應變能 EUmax和最大動能 Ekmax的表達式。那么，能量方程為

采用Ritz法對式（11）進行求解，可以得到

由式（12）可得到由3個方程組成的方程組，將此方程組采用矩陣的表達，可以得到特征方程：

式中，K、M分別為結(jié)構(gòu)系統(tǒng)的剛度矩陣和質(zhì)量矩陣；q為特征向量，q=(aM,bM,cM)Τ。

此時，K、M中的元素是所有待定參數(shù)的系數(shù)。為保證式（13）有解，需要系數(shù)矩陣的行列式為0，即

最后，對式（14）進行求解可得到特征方程的特征值，此特征值即為復合薄殼的某階次固有頻率。通過改變圓柱殼的周向波數(shù)n，并重復式（10）～式（14）的步驟可依次獲得各階模態(tài)的固有頻率。式（10）中，T的取值越大，固有頻率計算結(jié)果就越精確，通常取T=8即可達到足夠的精度。最后，將計算獲得的某階固有頻率對應的特征向量代入振型函數(shù) u(x,θ,t)、v(x,θ,t)和w(x,θ,t)，即可獲得復合薄殼結(jié)構(gòu)的某階模態(tài)振型。反復將獲得的不同階次的固有頻率代入式（13），可得到不同階次固有頻率對應的特征向量，將特征向量代入振型函數(shù)，就可依次獲得所關(guān)注的全部振型。

2 固有特性求解流程

2.1 輸入復合薄殼的幾何參數(shù)和材料參數(shù)

給出纖維增強復合薄殼的長度、半徑、厚度及每層纖維角度等幾何參數(shù)。然后，輸入纖維縱向和纖維橫向的彈性模量、剪切模量、泊松比和密度等材料參數(shù)，為后續(xù)動能和應變能的計算做好準備。

2.2 計算獲得最大動能

將位移（式（1））代入動能表達式（式（4）），得到用中面位移表示的動能的一般表達式，然后基于正交多項式法表示振型函數(shù)，并令表達式中的諧波分量 sin ωt=1，即可得到最大動能的表達式。

2.3 計算獲得最大應變能

在考慮纖維方向與整體坐標系X軸方向夾角θ的基礎上，首先利用應力-應變轉(zhuǎn)軸公式計算獲得每一層鋪層的應力（式（3）），隨后將應力、應變代入式（5）即可獲得每一層對應的用中面位移表示的應變能。然后，將每一層的應變能進行疊加，即可得到總應變能表達式。最后采用正交多項式來表示振型函數(shù)，并將其代入總應變能表達式中，可求得最大應變能。

2.4 采用Ritz求解固有頻率和模態(tài)振型

將上述步驟中計算獲得的最大動能和最大應變能代入式（11），可以獲得能量方程的表達式。根據(jù)Ritz法，將能量函數(shù)Π對所有待定參數(shù)求偏導，可以得到薄殼振動的特征方程（式（13）），對此特征方程求解特征值，可獲得纖維增強復合薄殼的一階固有頻率，通過改變圓柱殼的周向波數(shù)n，并重復式（10）～式（14）的步驟可依次獲得各階模態(tài)的固有頻率。最后將求得的固有頻率對應的特征向量代入振型函數(shù)中，即可獲得復合薄殼的全部振型。

3 實驗驗證

本文以T300碳纖維/環(huán)氧樹脂基復合薄殼為研究對象，對其固有特性進行了測試，薄殼長度為150 mm，內(nèi)半徑為132.5 mm，厚度為3 mm，安裝邊半徑為165 mm，安裝邊厚度為7 mm，密度ρ=1 570 kg/m3，纖維縱向彈性模量E1=134 GPa，纖維橫向彈性模量E2=8.5 GPa，剪切模量G12=3.36 GPa，泊松比 μ1=0.30。該類型復合薄殼為對稱正交鋪設，即[±4512]，共有24層，且每一鋪層具有相同的厚度和纖維體積分數(shù)。

本文研究的纖維增強復合薄壁圓柱殼的一端帶有安裝邊，在圓環(huán)壓板上擰緊12個M10螺栓來將復合圓柱殼固定到一個剛性和質(zhì)量都很大的夾具平臺上，夾具平臺通過多組螺栓實現(xiàn)與振動臺臺面的剛性連接。固定12個M10螺栓時，采用對稱安裝的方式，即先安裝兩個相對的螺栓，并不完全擰緊，當12個螺栓全部采用對稱安裝的方式固定之后，再用定力矩扳手以70 N·m的力矩將其擰緊，以此來保證較好的懸臂約束效果。

為了驗證本文所提出的懸臂邊界下纖維增強復合薄殼固有頻率計算方法的正確性，搭建了圖2所示的實驗系統(tǒng)來測試其固有頻率和振型。采用多點激勵單點響應測試的方法，對復合薄殼進行模態(tài)測試。

首先，建立其線框模型，并在模型上以每隔5°的間隔來設定錘擊點。然后，分別在復合圓柱殼的上、中、下3個圓周位置進行錘擊法模態(tài)實驗，測點總數(shù)為216。實際測試時，通過PCB 208C03模態(tài)力錘對復合薄殼進行脈沖激勵，使用Polytec PDV-100激光多普勒測振儀來獲取其振動響應，同時利用LMS16通道數(shù)據(jù)采集儀來獲得激勵和響應信號。表1給出了測試獲得的前8階固有頻率和振型。同時，為了便于比較，將通過MATLAB程序獲得的復合薄殼固有頻率的計算結(jié)果也列入表1，并對其誤差進行了詳細分析，表中的m、n分別為軸向半波數(shù)和周向波數(shù)。

圖2 纖維增強復合薄殼固有特性測試系統(tǒng)Fig.2 Natural characteristic test system of FRCS

通過與實驗結(jié)果進行對比可知，基于正交多項式法的纖維增強復合薄殼固有頻率計算結(jié)果與實驗結(jié)果之間的誤差范圍是2.2%～9.3%，處于誤差允許的范圍內(nèi)，且計算振型也與測試振型結(jié)果吻合度很高，進而驗證了所提出的固有特性計算方法的正確性，利用本文所提出計算方法可以較好地實現(xiàn)懸臂邊界下該類型復合薄殼固有特性的分析與預測。固有頻率的誤差可能來自于理論建模和實驗測試兩個方面。理論誤差包括在建模過

表1 計算和測試獲得的纖維增強復合薄殼前8階固有頻率和模態(tài)振型Tab.1 The first 8 natural frequencies and modal shapes of FRCS obtained by calculation and test

程中沒有考慮橫向剪切應力、纖維排列不規(guī)則、界面缺陷、殘余應力以及復合材料參數(shù)分散性的影響；實驗過程中的諸多因素也會導致誤差的產(chǎn)生，如測試時的邊界條件（夾具夾緊程度）不準確、儀器靈敏度漂移、錘擊點偏離、實驗方法不當?shù)仍斐傻挠绊憽?/p>

4 結(jié)論

（1）推導了具有k層纖維增強薄殼的應變能和動能，并計算了懸臂狀態(tài)下纖維增強薄殼的固有頻率和振型。

（2）給出了計算纖維增強復合薄殼固有特性的4個關(guān)鍵步驟：輸入復合薄殼的幾何參數(shù)和材料參數(shù)；獲得復合薄殼的最大動能；獲得復合薄殼的最大應變能；求解固有頻率和振型。

（3）以TC300碳纖維/樹脂復合薄殼為研究對象，計算獲得了其固有頻率和振型，并將其與測試結(jié)果進行了對比，固有頻率誤差范圍是2.2%～9.3%，且計算振型也與測試振型結(jié)果吻合得很好，驗證了理論計算方法的正確性。

［1］ 牛義，劉權(quán)利，常永樂，等.基于Ritz法的纖維增強復合薄板阻尼分析與預測［J］.中國工程機械學報，2016，14（2）：162-167.NIU Yi，LIU Quanli，CHANG Yongle，et al.Damping Analysis on Fiber-reinforced Composite Thin Plate on Ritz Method［J］.Chinese Journal of Construction Ma?chinery，2016，14（2）：162-167.

［2］ 崔海坡，溫衛(wèi)東.復合材料層合板沖擊損傷影響因素分析［J］.中國機械工程，2008，19（5）：613-617.CUI Haipo，WEN Weidong.Influence Factor Analysis for Impact Damage of Composite Laminates［J］.China Mechannical Engineering，2008，19（5）：613-617.

［3］ QATU M S，SULLIVAN R W，WANG W.Recent Re?search Advances on the Dynamic Analysis of Compos?ite Shells：2000-2009［J］.Composite Structures，2010，93（1）：14-31.

［4］ 薛鵬程，李暉，常永樂，等.懸臂邊界下纖維增強復合薄板固有頻率計算及驗證［J］.航空動力學報，2016，31（7）：1754-1760.XUE Pengcheng，LI Hui，CHANG Yongle，et al.Natu?ral Frequency Calculation and Validation of Fiber Re?inforced Composite Thin Plate under Cantilever Bound?ary［J］.Journal of Aerospace Power，2016，31（7）：1754-1760.

［5］ YOKOYAMA N O，DONADON M V，ALMEIDA S D.A Numerical Study on the Impact Resistance of Com?posite Shells Using an Energy Based Failure Model［J］.Composite Structures，2011，93（1）：142-152.

［6］ XU W，WAAS A M.A Novel Shell Element for Qua?si-static and Natural Frequency Analysis of Textile Composite Structures［J］.Journal of Applied Mechan?ics，2014，81（8）：081002.

［7］ SON B J，JI H S，CHANG S Y.A Study on Edge Rein?forcement Effect of Cylindrical Shells with Composite Laminate［J］.The Journal of the Korean Society for Ad?vanced Composite Structures，2012，3（2）：47-54.

［8］ AZARAFZA R，KHALILI S M R，JAFARI A A，et al.Analysis and Optimization of Laminated Composite Cir?cular Cylindrical Shell Subjected to Compressive Axial and Transverse Transient Dynamic Loads［J］.Thinwalled Structures，2009，47（8/9）：970-983.

［9］ LI H，SUN W，ZHAI J，et al.Precise Measurement of Natural Frequencies and Mode Shapes of Cantilever Thin Cylindrical Shell［J］.Journal of Vibration Engi?neering&Technologies，2015，3（4）：513-537.

［10］ RIBEIRO P.On the Influence of Membrane Inertia and Shear Deformation on the Geometrically Non-lin?earVibrations ofOpen， Cylindrical， Laminated Clamped Shells［J］.Composites Science&Technolo?gy，2009，69（2）：176-185.

［11］ HASHEMIAN A H，KARGARNOVIN M H，JAM J E.Accurate Calculation of the Natural Frequencies of Reticulated and Solid Cylindrical Composite Shells［J］.Applied Mechanics&Materials，2011，110/116：4598-4606.

［12］ CHEN H S，LI T Y，ZHU X，et al.Analysis of Natural Frequency of Free Damping Composite Cylindrical Shell Submerged in Viscous Fluids［J］.Materials Re?search Innovations，2015，18（2）：971-977.

［13］ 宋旭圓.層合薄壁圓柱殼結(jié)構(gòu)的非線性振動特性研究［D］.大連：大連理工大學，2016.SONG Xuyuan.Nonlinear Vibration Characteristics of Laminated Thin-walled Cylindrical Shell［D］.Da?lian：Dalian University of Technology，2016.

［14］ 項爽.旋轉(zhuǎn)功能梯度材料圓柱殼的振動特性研究［D］.河南科技大學，2013.XIANG Shuang.Free Vibration of Rotating Function?ally Graded Cylindrical Shells［D］.Luoyang：Henan University of Science and Technology，2013.

［15］ 李學斌.懸臂正交各向異性圓柱殼的自由振動分析［J］.艦船科學技術(shù)，2008，30（1）：41-44.LI Xuebin.Free Vibration of Cantilever Orthotropic Circular Cylindrical Shell［J］.Journal of Ship Science and Technology，2008，30（1）：41-44.

［16］ 戴亦俊.含液體分層復合材料薄壁圓柱殼振動分析［D］.沈陽：東北大學，2010.DAI Yijun.The Nonlinear Vibration Analysis of the Multi-layered Thin-cylindrical Shell Filled with Fluid［D］.Shenyang：Northeastern University，2010.

［17］ 樓玲娜.復合材料薄壁圓柱殼的非線性振動研究［D］.沈陽：東北大學，2009.LOU Linna.The Nonlinear Vibration Analysis of Composite Thin Cylindrical Shell［D］.Shenyang：Northeastern University，2009.