κ?μ陰影衰落信道下非數據輔助的誤差矢量幅度性能分析

楊凡，曾孝平，毛海偉，簡鑫，杜得榮，譚曉衡，高乙文

（1. 重慶大學通信工程學院，重慶 400044；2. 重慶金美通信有限責任公司，重慶 400030；3. 中國移動通信集團重慶有限公司，重慶 400044）

1 引言

κ?μ陰影衰落信道作為一種廣義的衰落信道，由Yacoub[1]首次提出，它具有與實際信道測試數據一致性好且能退化為多種典型衰落信道（Rice信道和Nakagami-m信道等）的特點[2]。κ?μ陰影衰落信道下的性能預測可為自適應調制策略設計、傳輸容量優化等無線通信中的關鍵技術提供有效的理論參考而受到國內外的廣泛關注。但由于在κ?μ陰影衰落信道下尚未給出理論的性能界限，無法給實際的系統設計提供有效的理論依據，因此，如何選擇信道評估參量并在κ?μ陰影衰落信道下進行性能分析就成為研究的核心問題。

信道質量分析的關鍵在于評估信道的物理量能夠實時準確地反映信道變化。一般常采用誤比特率（BER, bit error rate）和接收符號的信噪比（SNR,signal to noise ratio）來進行準靜態信道的質量評估[3]，而應用在κ?μ陰影衰落信道下，BER因為需要根據譯碼后的結果進行統計，統計結果遠滯后于信道變化；SNR估計常依賴于輔助數據（如前導符號和導頻符號）完成，也存在由于輔助數據間的固定時間間隔導致信道評估的非實時性誤差。隨著研究的深入，研究人員提出將誤差矢量幅度（EVM, error vector magnitude）作為特征參量，在時變衰落信道下評估信道質量的變化[4～6]。將EVM應用于評估信道質量的研究尚處于起步階段，有限的研究也僅基于輔助數據符號的EVM（DA-EVM, data-aided error vector magnitude）的測試與計算[7～9]，并沒有從理論上建立衰落信道下EVM的數學模型，無法推廣到更為一般的κ?μ陰影衰落信道中；文獻[10]利用SNR作為中間變量，推導了DA-EVM在基于MRC傳輸模型下κ?μ陰影衰落信道的理論表達式，并在此基礎上進行退化，給出了幾種典型信道下的DA-EVM閉合式，文獻[10]首次建立了利用DA-EVM分析κ?μ陰影衰落信道的理論體系架構，但由于輔助數據固定間隔帶來的非實時統計誤差，文獻[10]中DA-EVM的解析式不能有效地應用于κ?μ陰影衰落信道下的快時變場景。針對上述問題，并考慮到實際通信系統多采用非輔助數據接收，有學者提出采用非輔助數據符號的 EVM（NDA-EVM,nondata-aided error vector magnitude）對衰落信道進行分析[11]。NDA-EVM有以下優點：1)NDA-EVM對于無線信道衰落極為敏感，衰落引起接收符號的細微變化即會引起NDA-EVM較大的波動；2)不同于數據輔助的SNR和EVM估計，NDA-EVM估計不需要對比譯碼后的輔助數據，這樣即使在數據傳輸失敗的場景下，依然可以獲得NDA-EVM信息，并據此預測出當前信道條件下通信系統可能達到的性能（如誤符號率和吞吐量）[12]。目前，衰落信道下的NDA-EVM理論分析僅針對某些典型信道，如文獻[11]給出了NDA-EVM在Reyleigh信道下的計算模型，測試結果表明理論值與實際測試值有很高的一致性，可對Reyleigh衰落信道下系統的性能進行有效預測，然而文獻[11]并未將NDA-EVM對典型衰落信道表達式推廣至更為一般的κ?μ陰影衰落信道，其難點在于NDA-EVM對衰落信道定量分析需要給出閉合的解析式，而NDA-EVM在衰落信道下的建模具有很強的復雜性；同時NDA-EVM對κ?μ陰影衰落信道解析式也需要建立NDA-EVM與κ?μ分布關系，但此關系迄今依然是一個公開的問題，尚未有明確的解答。

據此，本文給出了SISO系統中利用NDA-EVM分析κ?μ陰影衰落信道的理論方法。以信道的衰落因子為中間變量，建立了κ?μ陰影衰落信道與NDA-EVM的聯系；通過最大似然準則推導了MQAM符號在衰落信道下NDA-EVM的閉合式；并在上述基礎上給出NDA-EVM在κ?μ陰影衰落信道下的理論下限，通過靈敏度分析進一步研究了信道參數對所推導下限的影響程度。經過仿真模擬，表明推導的下限值與理論值一致性較好，特別在低信噪比下有緊下界，且下限值對信道變化非常敏感，可為系統接收性能的準確預測提供理論支撐。

2 NDA-EVM在κ?μ陰影衰落信道的理論界限

κ?μ陰影衰落信道下NDA-EVM理論分析的基本思路是以MQAM信號在單輸入單輸出（SISO,single-input single-output）系統傳輸為系統背景，推導κ?μ陰影衰落信道下衰落因子的概率密度函數以及NDA-EVM的計算模型，以信道衰落因子為中間變量建立NDA-EVM與κ?μ陰影衰落信道之間的聯系，由此推導出NDA-EVM的理論界限。

2.1 信道衰落因子在κ?μ陰影衰落信道下的概率密度函數

在SISO系統中，MQAM信號在κ?μ陰影衰落信道下的模型可表示為

其中，n均值為0、功率譜密度為的復高斯隨機過程，；信道歸一化衰落因子為α，信號包絡能量的概率分布函數[13]為

其中，1F1(·)為Kummer超流函數。由文獻[13]的結論和SISO系統單天線接收的特性，式(2)可以表示為

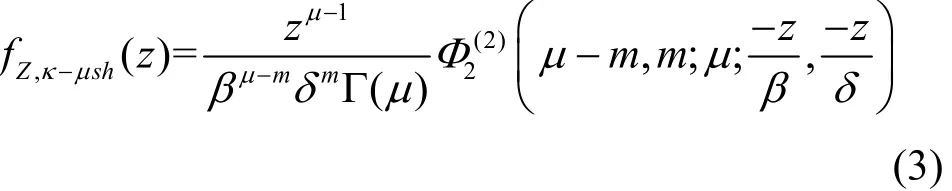
其中，為雙變量合流超幾何函數。由于2z=α，由式(3)可以進一步推出衰落因子α在κ?μ陰影衰落信道下的概率密度函數為

2.2 MQAM信號的NDA-EVM閉合解

NDA-EVM反映了接收符號與發送符號星座點的均方誤差，在實際的系統中，收發信機的非理想狀態（如功放工作在非線性區、載波泄露、I/Q不平衡等）和無線信道衰落是影響系統性能的2個典型方面，均會對NDA-EVM的評估產生影響。實際的通信系統，由于收發信機的工作狀態確定，所以設備的非理想狀態對NDA-EVM的影響是固定的，這種影響可采用射頻線纜連接收發信機的方式，通過儀器準確地度量出來。而信道的隨機特性，信道衰落對NDA-EVM的影響不是固定的，是隨信道參數改變而變化的。

接收端NDA-EVM的誤差評估是收發信機的非理想狀態和信道衰落這 2個方面影響的“線性疊加”，由于這 2個方面的因素彼此獨立，通過測量得出設備對NDA-EVM的影響后，就可以得出信道變化對NDA-EVM的影響。利用接收符號來計算NDA-EVM，由于接收符號受設備非理想和信道衰落的影響，估計出的NDA-EVM也反映了這2類影響因素的疊加，在除去測量得到設備非理想狀態下的NDA-EVM，就可以得出信道對NDA-EVM的影響。基于此，為了方便分析，本文假設收發信機是理想狀態，NDA-EVM僅受信道衰落影響，通過NDA-EVM來評估信道質量[11]，它可表示為

其中，y[i]是第i個接收符號，是由接收符號通過最大似然準則估計出的發送符號，為不失一般性，設P0=1。發送符號Si為M階的MQAM符號，可表示為

其中，因為MQAM符號實部和虛部具有對稱性，下文僅考慮實部用下標R表示，且省略收/發符號的索引號i，簡化式(5)為為歸一化幅度

由式(1)可知，接收符號的實部yR的條件概率密度函數可表示為

其中，?(·)為標準正態分布的概率密度函數。在最大似然準則下，由接收符號yR估計出發送符號為的概率為

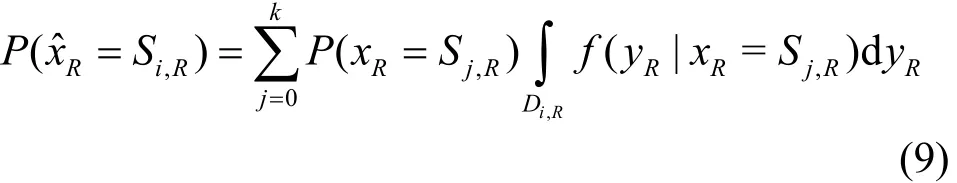
其中，Di,R為發送符號Si,R的判決域

由于發送符號等概率出現，可由條件概率求出

將式(9)和式(11)代入式(7)，可得

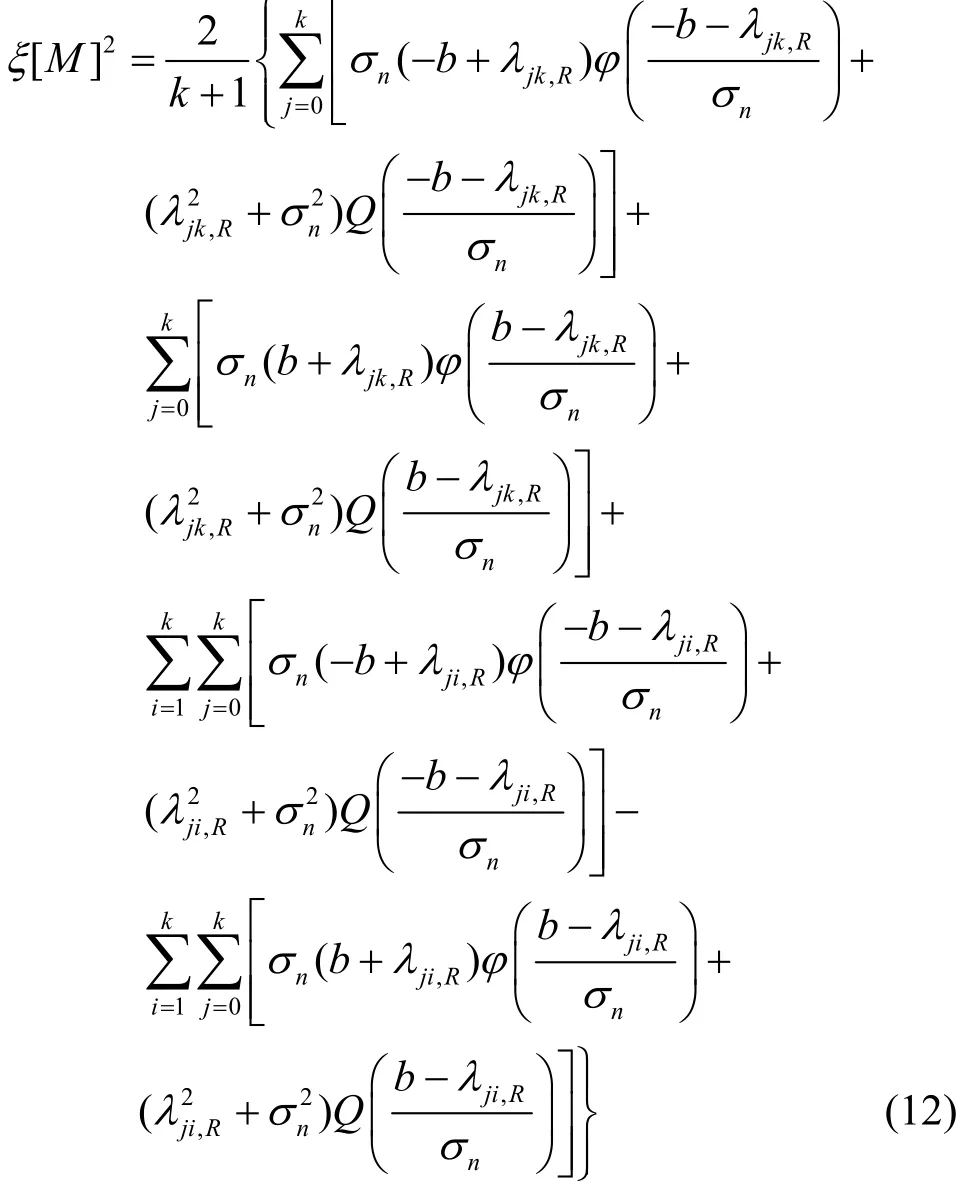
其中，Q(·)為互補累計分布函數，λji,R=?Si,R+αRSj,R。至此，式(12)給出了衰落信道下各調制階數NDA-EVM的統一計算模型。式(12)表示當調制階數為M的星座點被接收端依概率判決在Di,R域中3個區域時，每個區域中對應的EVM值的累加。

根據其物理意義，NDA-EVM可分為2個部分，第一部分為式(12)右邊中第一和第二個累加項，表示Di,R域中2個邊緣區域D0,R和Dk,R的EVM值，第二部分為后面2個累加項的差，表示1 ≤i≤k?1的中間區域Di,R的EVM值。由于第二部分恒為正值，且遠小于第一部分的EVM值。由式(12)可以表示為

考慮到μjk,R=b[α(j?k) + (αj?k)]＜ 0和Q(x)的單調遞減性，可得。又由于

同理，，式(13)可以進一步放縮為

根 據 Cauchy–Schwarz–Buniakowsky 不 等 式[14]，令bk=1，可得，由此，式(14)可表示為

其中，，化簡式(15)最終可得出NDA-EVM的下限為

2.3 κ?μ陰影衰落信道下NDA-EVM的下限

κ?μ陰影衰落信道下NDA-EVM的下限表示在該信道下NDA-EVM估計所能達到的最小值，它反映出當前信道環境MQAM信號在最佳接收時的星座點偏移，由此可以推算出在此信道狀態下系統可達到的最優性能（如自適應調制系統在當前信道條件下的最高調制階數以及系統可以達到的最低誤碼率），NDA-EVM下限可為無線傳輸系統的設計提供一個量化指標。

上文推導了衰落因子α在κ?μ陰影衰落信道下的概率密度函數，以及NDA-EVM在衰落信道下的解析式，以衰落因子α為中間變量，可以建立NDA-EVM在κ?μ陰影衰落信道下的模型。它可由κ?μ陰影衰落信道下的每一個瞬間衰落對應的NDA-EVM在該衰落因子α概率分布上的加權來量化。即

可以看出式(17)下限可由NDA-EVM的下限決定，由此將式(4)、式(16)代入式(17)可得2

令，將式(18)做積分變量替換后，可以表示為

其中，。在滿足的條件下，2(k)p1α≥ 。

由此，式(19)可進一步化簡為

利用文獻[15]中的性質

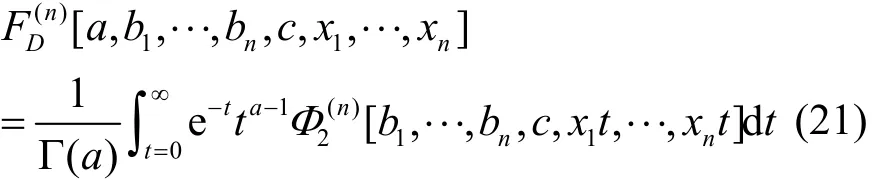
對式(20)進行化簡，最終得到不同調制階數的

NDA-EVM在κ?μ陰影衰落信道的下限成立的條件，需滿足0＜p＜μ。由此，式(22)的p最優值p?可通過對p進行優化求取。

值得注意的是，為了滿足

通過數值搜索的方法，不同調制階數的NDA-EVM在κ?μ陰影衰落信道的最緊下限可由最優的p?值確定。

2.4 NDA-EVM下限在幾種典型信道下的退化

κ?μ陰影衰落信道可以退化為幾種典型的信道，如Rice信道和Nakagami-m信道等，由此也可以得到NDA-EVM在這幾種典型信道下的下限。

1) Rice信道

當μ=1時，κ?μ陰影衰落信道可以化簡為Rice信道，此時的κ即為萊斯因子。由此可得

在Rice信道的下限可以簡化為

p最優值p?可表示為

為驗證NDA-EVM及其下限在Rice信道的有效性，將由式(12)得到的NDA-EVM值、式(24)得到的下限值以及LTE-A標準3GPP TS 36.101定義的EVM值進行對比[16]。Rice信道下( 1, 10μ=κ= )，當SNR=0 dB，α=0.8時，三者對比如表1所示。

表1 在Rice信道下NDA-EVM及其下限與LTE-A標準EVM典型值的對比

由表1可以看出，當κ?μ陰影衰落信道退化為 Rice信道，由本文算法求取的NDA-EVM與 LTE-A標準下的典型值較為接近，且各階調制模式下的NDA-EVM下限值與典型值的差異均小于8%。

2) Nakagami-m信道

當κ→0時，κ?μ陰影衰落信道可以化簡為Nakagami-m信道。由此可得。將其代入式(22)，可化簡為

由文獻[15]可知

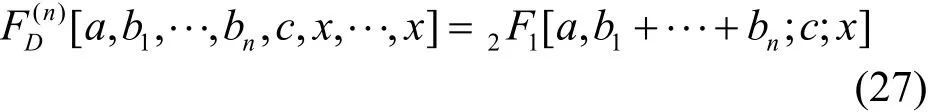
式(26)可進一步化簡，得到NDA-EVM在Nakagami-m信道的下限值為

其中，p最優值p?可表示為

同理，為驗證所推下限的有效性，在Nakagami-m信道(κ= 0.01,μ= 1時)下，對 LTE-A標準下的EVM典型值、NDA-EVM以及其下限值進行對比。當SNR=0 dB，α=0.9時，三者對比如表2所示。

表2 在Nakagami-m信道下NDA-EVM及其下限與LTE-A標準EVM典型值的對比

由表2可以看出，在Nakagami-m信道，NDAEVM與LTE-A標準下的典型值較為接近，且各階調制模式下的NDA-EVM下限值與典型值的差異均小于10%。

綜上可知，在κ?μ陰影衰落信道退化為 Rice和Nakagami-m典型信道時，NDA-EVM與LTE-A標準下的典型值一致，NDA-EVM的下限值放縮誤差小于 10%，可以對κ?μ陰影衰落信道進行有效的評估。

3 NDA-EVM特性的理論分析

3.1 下限的參數靈敏度分析

由式(22)可知，NDA-EVM下限受參數k、μ、κ的影響。參數靈敏度反映了信道參數κ、μ、調制階數對NDA-EVM下限的影響程度，通過靈敏度分析可發現NDA-EVM下限對哪些參數變化敏感，從而為分析不同信道下NDA-EVM的性能提供理論支撐。

第二，壟斷性國有企業的分類重組改造是國有企業混合所有制改革的必要條件。《關于國有企業功能界定與分類的指導意見》界定了三類國有企業，即主業處于充分競爭行業和領域的商業類國有企業；主業處于關系國家安全、國民經濟命脈的重要行業和關鍵領域，主要承擔重大專項任務的商業類國有企業；處于自然壟斷行業的國有企業。這三類企業的混合所有制改革方向、路徑和目標截然不同，需要分類處置。但是目前我們的國有企業，尤其是大型央企大多是三種業務兼而有之，甚至部分央企還承擔社會公益服務，綜合性業務采取一種混合所有制改革路徑顯然不適宜。因此，需要采取剝離、重組、整合、改造等手段，予以分類處置和歸一化處理[3-5]。

為了量化單參數變化對下限值的影響程度，NDA-EVM下限的靈敏度分析采用各參數的靈敏度系數進行定量評估。根據文獻[17]對靈敏度的定義，變量參數xi對系統y(x)的靈敏度系數Sxi可表示為

可以得到參數k、μ、κ的靈敏度系數，如表3所示。

圖1分別給出了調制參數k、信道參數μ、κ的靈敏度分析曲線。它們反映了其中任意一個變量在其余2個變量固定時對NDA-EVM下限的影響程度。

從圖1可以看出以下3點。1)，即調制階數對NDA-EVM下限值的影響最大，信道參數μ影響次之，信道參數κ影響最小。2)Sk、Sμ、Sκ均為負值，調制參數k、信道參數μ、κ均與NDA-EVM下限負相關，即任一參數變大，NDA-EVM在κ?μ陰影衰落信道的下限均會減小。3) 調制參數k、信道參數μ、κ的值由小變大，其靈敏度系數的絕對值由大變小并接近 0，表明隨著3種參數值變大，NDA-EVM下限趨于穩定，最終收斂。

表3 NDA-EVM下限的參數靈敏度

圖1 NDA-EVM下限的參數靈敏度分析

圖1 NDA-EVM下限的參數靈敏度分析（續）

3.2 低信噪比的緊下界

在求取NDA-EVM下限時，對NDA-EVM的閉合式進行放縮，放縮誤差的主要來源于式(12)對后2項中“2個累加項的差”的處理，下面分析低信噪比下的放縮誤差，記誤差項為

由此可知，在低信噪比條件下，誤差項趨近于0，其物理意義是：在信噪比很低的條件下，接收端的星座符號大量的偏離理想星座點，大概率的分布在Di,R域中2個邊緣區域D0,R和Dk,R，分布于中間區域Di,R的概率很小，計算NDA-EVM時可以將其忽略掉。

圖2給出了低信噪比情況下ε的變化情況，由圖 2可見，ε在低信噪比區，各個調制階數的NDA-EVM均趨近于0，與理論的分析吻合。

由于在低信噪比下，MQAM信號的NDA-EVM有緊下界，所以由式(16)推導出的NDA-EVM在κ?μ陰影衰落信道的下界在低信噪比區依然是緊下界。

3.3 NDA-EVM在κ?μ陰影衰落信道下的RMSE

為了驗證NDA-EVM評估κ?μ陰影衰落信道的準確性，本節利用最小均方誤差（RMSE, root mean square error）對比分析了NDA-EVM、DA-EVM和DA-SNR這3種信道評估參量。RMSE反映了信道估計值與真實值之間的差異，它定量給出了NDA-EVM、DA-EVM和DA-SNR的估計偏差。由于本文假設收發信機理想狀態，在不考慮設備誤差的情況下，RMSE的物理意義是3種信道質量評估參量受無線信道影響時的估計偏差。RMSE越小，表明信道質量評估值越接近實際值，越能準確地表征信道質量。由于實際信道具有隨機特性，實際的測試也只能反映某一時刻特定狀態的信道特征，無法反映所有參數變化對信道評估參量的影響，所以本文采用蒙特卡洛方法對不同的信道參數逐一掃描，模擬信道變化時NDA-EVM、DA-EVM和DA-SNR的評估準確性。為模擬信道的隨機特性，將大量發送數據通過不同信道參數的κ?μ陰影衰落信道，并記錄不同信道參數改變下，由式(12)估計算出的NDA-EVM值（記為Eξ），同時接收端利用蒙特卡洛算法，比較接收星座點與理想星座點的偏差，進行NDA-EVM測算，將其作為NDA-EVM在κ?μ陰影衰落信道下的真實值（記為ξR）。經過 105次測算后，由，可以計算出NDA-EVM的RMSE。同理，可得出DA-EVM和DA-SNR的RMSE。

圖3和圖4給出了NDA-EVM與傳統的信道質量評估量（DA-SNR和DA-EVM）在κ?μ陰影衰落信道下估值的均方誤差曲線。其中，輔助數據的分布為每100個數據符號插入1個已知序列的輔助數據符號。由圖3和圖4可知：隨著信道參數μ的減小，3種估計量的RMSE均增加，但NDA-EVM估計值與真實值更為接近，RMSE明顯低于傳統評估量，且μ值越小，NDA-EVM與對比統計量在RMSE上的差距越明顯，這是因為參數μ越小，信道衰落加劇引起的接收信號畸變越嚴重[18]，DA-EVM和DA-SNR估計速率受輔助數據固定間隔影響無法準確反映信道的快速變化；同理，隨著信道參數κ的減小，表明衰落造成的信號能量耗散增加[18]，接收信號惡化，但NDA-EVM估計同樣有最小的RMSE。說明NDA-EVM對κ?μ陰影衰落信道質量的評估更為準確，較傳統評估量也更為有效。

圖3 μ=1, κ變化時3種評估參量的RMSE

圖4 κ=1, μ變化時3種評估參量的RMSE

可以看出，NDA-EVM估計在不同的信道環境下均有比DA-EVM和DA-SNR低的估計誤差，其根本原因在于NDA-EVM不受輔助數據間隔的影響，信道質量評估實時性好。在實際的應用中，由于DA-EVM和DA-SNR是依靠輔助數據（如導頻、前導）來完成信道質量的測算，輔助數據的間隔決定了信道質量評估的速度，DA-EVM和DA-SNR顯然無法跟蹤信道的變化。特別是應用到數據分組或自適應調制這類對實時性要求較高的系統中，系統需要對信道質量實時評估以調整傳輸參數，以DA-EVM和DA-SNR為信道質量評估參量就會因為實時性差導致傳輸參數的選擇錯誤，影響系統性能。總之，NDA-EVM在信道質量估計的實時性和準確性上要優于DA-EVM和DA-SNR，可為實際通信系統中自適應調制門限的精確選取、時變信道下的傳輸策略優化以及系統接收性能的準確預測提供理論參考。

4 κ?μ陰影衰落信道下NDA-EVM的性能仿真

為了對NDA-EVM在κ?μ陰影衰落信道下可以達到的性能界限進行分析，本節采用蒙特卡洛法進行仿真實驗。仿真模擬了 SISO系統，對通過κ?μ陰影衰落信道的MQAM信號進行NDA-EVM測算，將經過105次測算的NDA-EVM算術平均后作為其在κ?μ陰影衰落信道下的理論值，通過與文本估計值進行仿真對比，分析不同信道參數下NDA-EVM的性能。

4.1 不同調制階數MQAM符號的NDA-EVM下限

圖5給出了在κ?μ陰影衰落信道下NDA-EVM下限在不同調制階數下的性能。信道參數為κ= 0.85，μ=0.55，在此信道參數下通過數值搜索確定出各調制階數NDA-EVM下限值的最優p*，其中QAM(p*= 0.28)，16QAM(p*= 0.26)，64QAM(p*= 0.2025)。由圖5可知：1) 低信噪比下NDA-EVM在κ?μ陰影衰落信道的下限接近理論值，這種特性在第3.2節中進行了詳細的分析。值得注意的是，當信噪比不斷增加時，NDA-EVM的下限值不斷減小直至收斂；2)NDA-EVM在κ?μ陰影衰落信道的下限值受調制階數的影響較大，調制階數越高，NDA-EVM下限越低，這種現象可由調制階數對NDA-EVM下限的靈敏度特性得出解釋。

圖5 不同調制階數MQAM符號在κ?μ陰影衰落信道下的NDA-EVM下限

4.2 不同信道參數μ的NDA-EVM下限

圖6比較了QAM信號在μ參數變化時NDA-EVM下限與理論值的性能差異。由圖6可知：1) 低信噪比使NDA-EVM下限值逼近于理論值，隨著信噪比增加NDA-EVM下限最終收斂；2) 隨著信道參數μ的增加，NDA-EVM下限值不斷降低，這是由于參數μ表示了衰落信道的直視徑能量的集中程度[2]，參數μ越大，直視徑能量越集中，NDA-EVM有較低的下限值。同時，由靈敏度分析可知，參數μ對下限值的影響較大，較小的μ變化將造成NDA-EVM下限的較大波動。

圖6 不同信道參數μ的NDA-EVM下限

4.3 不同信道參數κ的NDA-EVM下限

圖7比較了QAM信號在κ參數變化時NDAEVM下限與理論值的性能差異。

圖7 不同信道參數κ的NDA-EVM下限

由圖7可知：1) 與前文分析一樣，在不同信道參數κ的衰落信道中，NDA-EVM下限與理論值在低信噪比下有較小差距，隨著信噪比增加NDA-EVM下限最終收斂；2) 隨著信道參數κ的增加，NDA-EVM下限值不斷降低，這是由于參數κ表示了信道衰落下接收端信號能量的集中程度[2]，參數κ越大，衰落造成的能量耗散越小，因此NDA-EVM有較低的下限值。同時，由參數的靈敏度分析可知，相較其他參數，κ的變化對NDA-EVM下限的影響最小。

5 結束語

本文提出一種基于NDA-EVM對κ?μ陰影衰落信道進行理論分析的方法。通過最大似然準則建立了衰落信道下NDA-EVM統一的計算模型；并以衰落因子為中間變量，建立了NDA-EVM與κ?μ分布的聯系，據此推導了NDA-EVM在κ?μ陰影衰落信道的理論表達式，給出了NDA-EVM在κ?μ陰影衰落信道可能達到的理論下限，并化簡了理論下限在幾種典型信道（Rice信道和Nakagami-m信道）下的退化表達式。進一步地，對所推導的NDA-EVM下限進行參數靈敏度、緊下界以及信道評估參量的RMSE對比分析，并通過仿真模擬NDA-EVM在κ?μ陰影衰落信道下的性能。結果表明：1) 相較傳統的DA-SNR和DA-EVM，NDA-EVM對κ?μ陰影衰落信道的評估具有更小的RMSE值，評估結果更為準確有效；2) 推導的NDA-EVM下限在低SNR區域更接近理論值；3)NDA-EVM在κ?μ陰影衰落信道的理論下限受到調制階數、參數κ和μ的影響，其中受調制階數影響程度最大，參數μ次之，

參數κ最小；4) 理論下限均與調制階數、參數κ和μ負相關變化，即理論下限均隨著參數的增大而降低。簡言之，NDA-EVM在κ?μ陰影衰落信道定量分析具有廣泛的理論意義和工程應用價值，可為自適應調制門限的精確選取、時變信道下傳輸策略的優化以及系統接收性能的準確預測提供理論參考。

[1] YACOUB M D. Theκ-μdistribution∶ a general fading distribution[C]//Vehicular Technology Conference, 2001∶ 1427-1431.

[2] YACOUB M D. Theκ-μdistribution and theη-μdistribution[J]. IEEE Antennas and Propagation Magazine, 2007, 49(1)∶ 68-81.

[3] HANZO L, NG S X, WEBB W T, et al. Quadrature amplitude modulation∶ from basics to adaptive trellis-coded, turbo-equalised and space-time coded OFDM, CDMA and MC-CDMA systems[M]. IEEE Press-John Wiley, 2004.

[4] SHAFIK R A, RAHMAN M S, ISLAM A H M R, et al. On the error vector magnitude as a performance metric and comparative analysis[C]// ICET'06. International Conference on Emerging Technologies,2006∶ 27-31.

[5] 周峰, 張睿, 高攸綱, 等. 五種失真因素綜合作用下的 EVM[J]. 電子學報, 2012, 40(3)∶ 607-610.ZHOU F, ZHANG R, GAO Y G, et al. Error vector magnitude by five distortion factors[J]. Acta Electronica Sinica, 2012, 40(3)∶ 607-610.

[6] 游長江, 朱曉維, 柳靖, 等. 基于射頻前端的動態頻譜共享無線通信系統工作信道選擇分析[J]. 通信學報, 2011, 32(4)∶ 147-152.YOU C J, ZHU X W, LIU J. Analysis of operational channel selection of dynamic spectrum sharing wireless communication system based on RF front-end[J]. Journal on Communications, 2011, 32(4)∶ 147-152.

[7] CHOUITEM R. EVM based AMC for an OFDM system[C]//Wireless Telecommunications Symposium (WTS), 2010. IEEE, 2010∶ 1-5.

[8] LIU R, LI Y, CHEN H, et al. EVM estimation by analyzing transmitter imperfections mathematically and graphically[J]. Analog Integrated Circuits and Signal Processing, 2006, 48(3)∶ 257-262.

[9] GEORGIADIS A. Gain, phase imbalance, and phase noise effects on error vector magnitude[J]. IEEE Transactions on Vehicular Technology,2004, 53(2)∶ 443-449.

[10] THOMAS V A, KUMAR S, KALYANI S, et al. Error vector magnitude analysis of fading SIMO channels relying on MRC reception[J].IEEE Transactions on Communications, 2016, 64(4)∶ 1786-1797.

[11] MAHMOUD H A, ARSLAN H. Error vector magnitude to SNR conversion for nondata-aided receivers[J]. IEEE Transactions on Wireless Communications, 2009, 8(5)∶ 2694-2704.

[12] SEN S, SANTHAPURI N, CHOUDHURY R R, et al. AccuRate∶constellation based rate estimation in wireless networks[C]//NSDI.2010∶ 175-190.

[13] PARIS J F. Statistical characterization ofκ-μshadowed fading[J].IEEE Transactions on Vehicular Technology, 2014, 63(2)∶ 518-526.

[14] ALAN J, DANIEL Z. Table of integrals, series and products (7th ed)[M]. New York∶ Academic, 2007.

[15] EXTON H. Multiple hypergeometric functions and applications[M].Halsted Press, Ellis Horwood, 1976.

[16] 3GPP TS 36.101. User Equipment (UE) radio transmission and reception[S]. 2010.

[17] SALTELLI A, CHAN K, SCOTT E M. Sensitivity analysis[M]. New York∶ Wiley, 2000.

[18] COTTON S L. Second-order statistics ofκ-μshadowed fading channels[J]. IEEE Transactions on Vehicular Technology, 2016, 65(10)∶8715-8720.