基于有限序列的壓縮新算法
趙宏偉,劉宇琦,特日根,陳長征,臧雪柏,3
(1.吉林大學 計算機科學與技術學院,長春 130012;2.中國科學院 應用光學國家重點實驗室,長春 130033; 3.吉林大學 符號計算與知識工程教育部重點實驗室,長春 130012;4.長光衛星技術有限公司,長春 130000)
0 引 言
數據業務和多媒體通信業務等通信量越來越大,給信息存儲特別是網絡傳輸帶來前所未有的壓力。現有數據壓縮算法分為無損壓縮和有損壓縮。有損壓縮通過數據挖掘等手段從數據來源、數據特性出發,提取關鍵信息予以保存。語音識別、市場銷售數據、氣象數據、電信通信數據等均可采用有損壓縮方法處理。針對這種數據的有損壓縮通常有兩類辦法[1]:數據匯聚和數據近似。匯聚函數以拋棄數據中的原始結構為代價,減少數據量,但這種方法使得一些有用的知識被刪除,其中主要包括COUNT、SUM、AVG等方法;數據近似[2]可視為基于模型的數據獲取,通過對采集到的感知數據進行分布式建模,可減少數據傳輸量、節省網絡能量、延長網絡生命。有損壓縮方法可分為基于概率模型[3]、基于時間序列分析模型[4]、基于數據挖掘模型[5]、基于數據壓縮模型[6]4類,其共性在于壓縮率高,數據還原質量依賴于算法實現的代價。
無損壓縮技術[7]在數據壓縮過程中不允許損失精度,可以保真還原。主要用于文本文件、數據庫、程序數據和特殊應用場合的圖像數據(如指紋圖像、醫學圖像)等壓縮。游程長度編碼[8]通過去除文本中的冗余字符或字節中的冗余位,達到減少數據文件所占的存儲空間的目的,其壓縮效能取決于整個數據流的重復字符出現次數、平均游程長度以及所采用的編碼結構。由于該算法是針對文件的某些特點所設計的,具有一定的局限性。G?del[9]提出一種不依賴于數據庫的無損壓縮方法,稱為哥德爾數方法,但其使用范圍局限于對圖靈機程序的壓縮,因此不具有普遍性。
本文提出了CSNB(Compress sequence number-Binary)壓縮算法,通過增加校驗位的形式實現壓縮。
1 壓縮排序數
1.1 CSNB
定義1 對于任意序列,其對應的最小字長的二進制序列為原序列的CSNB序列。
例:若序列為1,3,2,6,5,4,則CSNB序列為001,011,010,110,101,100。
定義2 任意1到n的全排列序列,通過式(1)計算得到的二進制數為此序列的奇偶校驗碼CSNBc:
⊕
(1)
式中:N⊕表示在二進制數N中每位依次求異或所得到的值;CSNBi為CSNB序列中的第i個數。
例:若序列為1,3,2,6,5,4,CSNB序列為001,011,010,110,101,100,則奇偶校驗碼的計算過程為:
001⊕=1;011⊕=0;010⊕=1;
110⊕=0;101⊕=0;100⊕=1
CSNBc為100101。
定義3 任意CSNB序列,通過式(2)計算所得的值為CSNB序列的前序錯位求和部分CSNF。
(2)
定義4 任意CSNB序列,通過式(3)計算所得的值為CSNB序列的后序錯位求和部分CSNA。
(3)

定義5 任意CSNB序列,通過式(4)計算所得的值為CSNB序列的CSNB。

10n×CSNA+CSNBc
(4)
因為CSNB序列為二進制序列,所以式(4)為二進制計算。
例:CSNB序列為:001,011,010,110,101,100

10n×CSNA+CSNBc=101111×
(100×1+101×11+1010×10+
1011×110+10100×101+10101×100)+
10110×(100×100+101×101+1010×110+
1011×10+10100×11+10101×1)+
100101=10000111110000110100101
1.2 CSNB與原序列的比較
原序列以十進制的方式記錄排序序列。計算機對十進制數常用的編碼方式是BCD碼,以16位計算機為例,在記錄十進制數時計算機會為每個十進制數預留16位。而CSNB序列是以二進制的方式記錄排序序列,計算機在記錄時不需要編碼轉換。其對比結果如表1所示。
原序列、CSNB序列以及CSNB都具有記錄序列的功能,其空間復雜度對比結果如表2所示(計算機為k位)。

表1 原序列與CSNB序列的比較Table 1 Comparison of original sequence and sequence CSNB

表2 CSN序列、CSNB序列以及CSNB占用空間對比Table 2 CSN sequence,CSNB sequence and CSNB space comparison bit
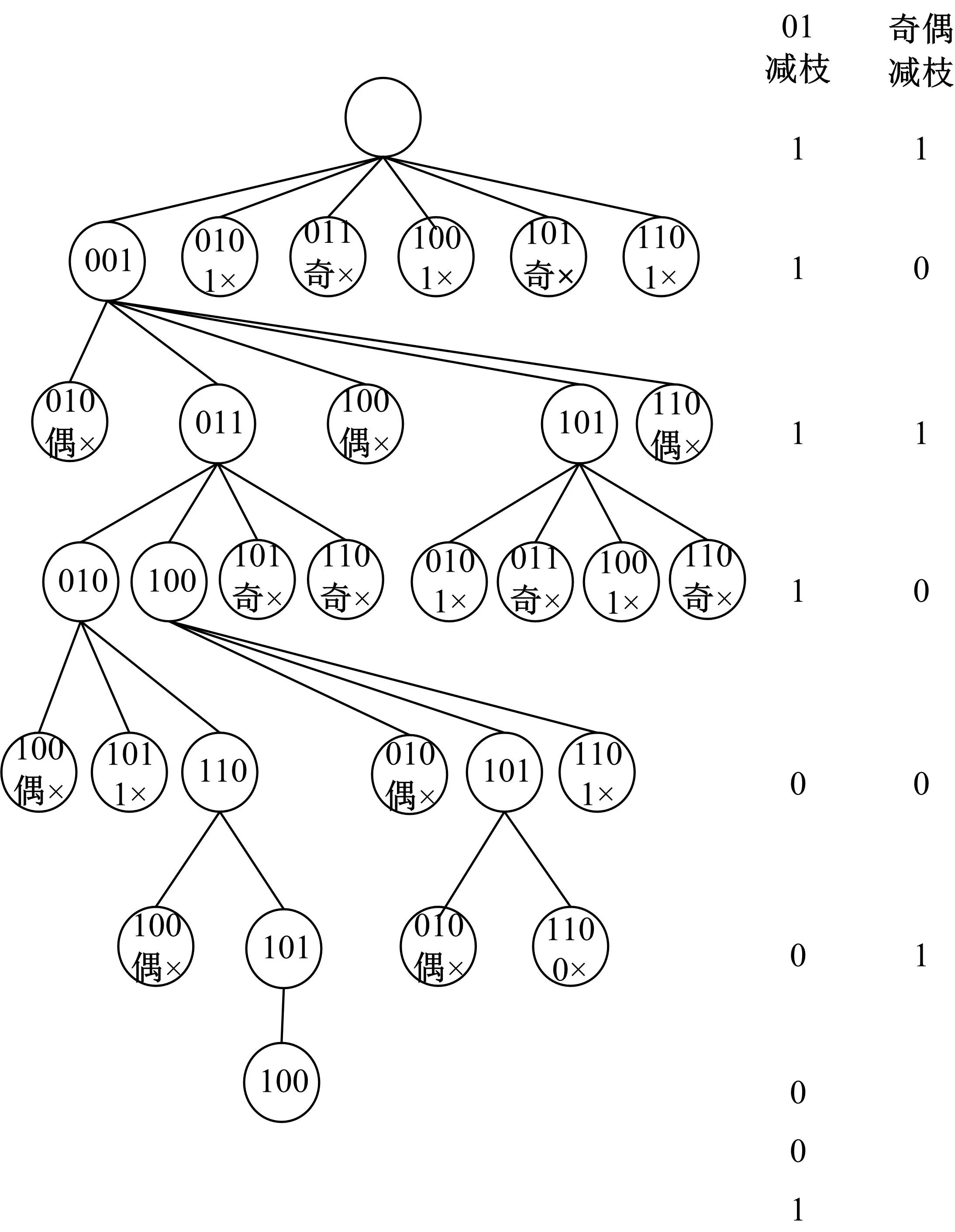
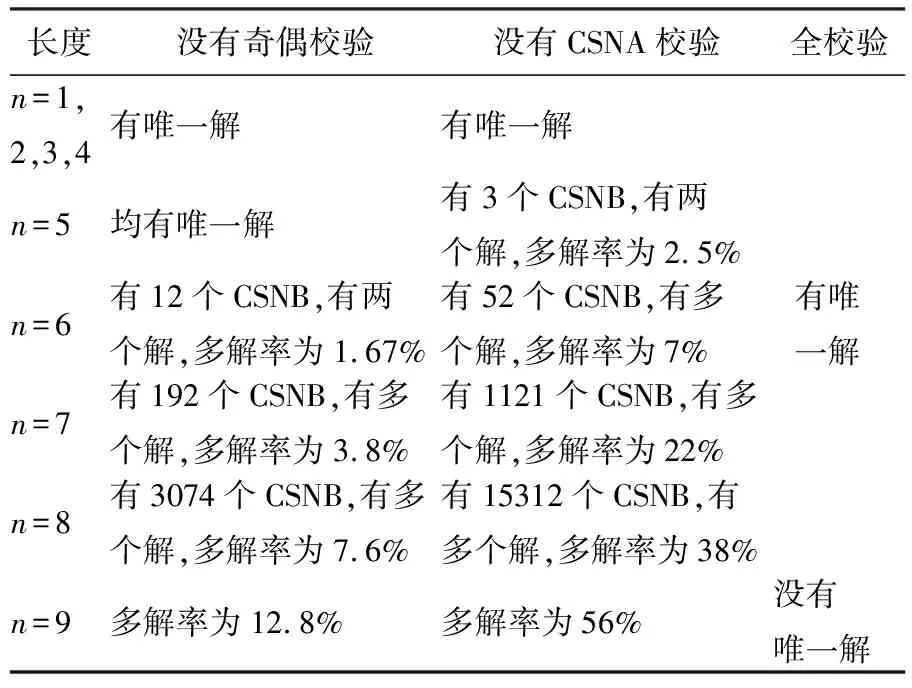
由表2可知,當序列長度n≤8時,CSNB序列較CSNB有更好的空間利用率,且CSNB序列并沒有進行改裝壓縮,所以也不需要繁瑣的解壓過程,但當8 定義6 如果一個節點N的奇偶校驗碼為N⊕1,其祖先節點要求的奇偶校驗碼為1,且N⊕1≠1,則剪枝發生在該節點之上,此時,稱該剪枝過程為奇剪枝。 定義7 如果一個節點N的奇偶校驗碼為N⊕1,其祖先節點要求的奇偶校驗碼為0,且N⊕1≠0,則剪枝發生在該節點之上,此時,稱該剪枝過程為偶剪枝。 定義8 如果一個在第n層(根節點為第0層)的節點N與回溯到根節點中所有遍歷到的節點進行式(3)的計算,得到結果的倒數第n位為C,其祖先節點要求的01校驗碼為1,且C≠1,則剪枝發生在該節點之上,此時,稱該剪枝過程為1剪枝。 定義9 如果一個在第n層(根節點為第0層)的節點N與回溯到根節點中所有遍歷到的節點進行式(3)的計算,得到結果的倒數第n位為C,其祖先節點要求的01校驗碼為0,且C≠0,則剪枝發生在該節點之上,此時,稱該剪枝過程為0剪枝。 性質1 由于奇偶剪枝不需要累加運算,且在選定下一節點時可直接計算,并且奇偶剪枝針對的是真實的排序值,所以奇偶剪枝較01剪枝速度更快、效率更高。 雖然通過決策樹的剪枝方法能夠刪掉大多數非解節點,但剪枝后的決策樹仍然可能存在多個所在層為n的葉子節點,所以還需要通過CSNA對所有可能解進行檢驗。 例:CSNB序列為:001,011,010,110,101,100,CSNB=100001111100101,其剪枝策略如圖1所示,先進行奇偶校驗,再進行01校驗。其中,“奇×”、“偶×”、“1×”和“0×”分別表示進行奇剪枝、偶剪枝、1剪枝和0剪枝操作。 圖1 剪枝策略示意圖Fig.1 Pruning strategy schematic 創建決策樹是從邏輯的角度分析算法的執行過程,本質上解壓算法并不需要構建決策樹。決策樹在選擇節點時,是通過剪枝策略來判斷其選擇的節點是否正確,從邏輯角度來說,是嘗試著確定CSNBi的位置。 根據式(2)求CSNBi,本質上是在求以CSNB1,CSNB2,…,CSNBn為未知數,方程CSNF=20×CSNB1+21×CSNB2+…+2n-1×CSNBn(方程為十進制方程)的解,其中當i≠j時,CSNi≠CSNj且1≤CSNi≤n。 而決策樹是在明確CSNBi值的情況下,去求其位置,即為求以x1,x2,…,xn為未知數,方程CSNF=2x1×CSNB1+2x2×CSNB2+…+2xn×CSNBn(方程為十進制)的解,其中當i≠j時,xi≠xj且1≤xi≤n-1。 根據以上分析,可制定CSNB解壓算法的步驟如下所示。 (1)建立記錄所有未知數狀態的未知數狀態表(Statetable),所有未知數的初始狀態是Uncertain。若未知數個數為n,則未知數的其他可能狀態數為[1,n]中的整數。 (2)從Statetable中提取一個未被測試過的且狀態為Uncertain的未知數,并執行第(3)步。如果不存在符合條件的未知數,則執行第(5)步。 (3)將選定的未知數依次通過奇偶檢驗和01檢驗,如果都通過,則執行第(4)步;否則,將此未知數視為已檢測狀態,并執行第(2)步。 (4)將選定的未知數的初始狀態更改為未被選定的狀態中最小的狀態數,將其他狀態為Uncertain的未知數均視為未被測試狀態,執行第(2)步。 (5)若Statetable中仍存在狀態為Uncertain的未知數,則將狀態數最大的未知數以及之后的未知數狀態設定為Uncertain,將之后的未知數視為未檢測狀態,并繼續執行第(2)步;否則執行第(6)步。 (6)通過CSNA判斷找到的可能解的正確性,若正確,算法結束;否則,將狀態數最大的未知數以及之后的未知數狀態設定為Uncertain,將之后的未知數視為未檢測狀態,并執行第(2)步。 所謂正向檢驗,就是給定任意排列的CSNB,由CSNB解其原序列,若解唯一,不僅能說明CSNB系統的正確性,還能檢驗解壓算法的正確性。 任意長度為n的CSNB序列,其全排列的總數為n!,當n=9時,一共有9!=362880種排列情況,一一測試是不合理的,所以當1 表3 正向檢驗解的唯一性Table 3 Positive test uniqueness of the solution 由表3可知,CSNA的查錯率更高。假設沒有奇偶校驗和沒有CSNA校驗的多解率符合某種概率分布,且是相互獨立的,則當5 所謂反向檢驗,就是給定任意排列的CSNB,計算是否存在一個不同的CSNB序列的CSNB與其相同,若存在則解不唯一;若不存在則解唯一。通過對比正向檢驗和反向檢驗的結果可知解壓算法的正確性。 任意長度為n的CSNB序列,其全排列的總數為n!,通過與其所有不同的CSNB序列作對比,其比較次數為n!!。當n=9時,一共有9!!=362880!次比較,這樣測試是不合理的,所以采用與正向檢驗相同的方法對其進行反向檢驗,即當1 表4 反向檢驗解的唯一性Table 4 Uniqueness of the solution of reverse test 研究了排序序列的記錄及存儲方式,提出了CSNB的存儲方式,CSNB中包含有前序錯位求和CSNF、后序錯位求和CSNA以及奇偶校驗碼3部分。CSNB通過對排序序列進行壓縮,其空間復雜度為O(log2n+n)。通過解壓算法可找到對應的原序列,實現序列還原。CSNB的壓縮不僅可以使其具有更好的空間利用率,而且能夠增加信息傳遞的可靠性。 參考文獻: [1] Deligiannakis A,Kotidis Y,Roussopoulos N. Dissemination of compressed historical information in sensor networks[J]. The VLDB Journal,2007,16(4):439-461. [2] 張建明,林亞平,周四望,等. 傳感器網絡中誤差有界的小波數據壓縮算法[J]. 軟件學報,2010,21(6):1364-1377. Zhang Jian-ming,Lin Ya-ping,Zhou Si-wang,et al. Haar wavelet data compression algorithm with error bound for wireless sensor networks[J]. Journal of Software,2010,21(6):1364-1377. [3] Chu D,Deshpande A,Hellerstein J M,et al. Approximate data collection in sensor networks using probabilistic models[C]∥Proceedings of the 22nd International Conference on Data Engineering,Atlanta,USA,2006:48-59. [4] Najafi H,Lahouti F,Shiva M. AR modeling for temporal extension of correlated sensor network data[C]∥International Conference on Software in Telecommunications and Computer Networks,Split, Croatia,2006:117-120. [5] Borgne Y L,Bontempi G. Unsupervised and supervised compression with principal component analysis in wireless sensor networks[C]∥13th ACM International Conference on Knowledge Discovery and Data Mining,New York,USA,2007:94-103. [6] Ganesan D,Estrin D,Heidemann J. DIMENSIONS:Why do we need a new data handling architecture for sensor networks?[J]. ACM SIGCOMM Computer Communication Review,2003,33(1):143-148. [7] 鄭翠芳. 幾種常用無損數據壓縮算法研究[J]. 計算機技術與發展,2011,21(9):73-76. Zheng Cui-fang. Research of several common lossless data compression algorithms[J]. Computer Technology and Development,2011,21(9):73-76. [8] Tsang P,Liu J P,Cheung K. Modern methods for fast generation of digital holograms[J]. 3D Research,2010,1(2):11-18. [9] G?del K. über formal unentscheidbare S?tze der Principia Mathematica und Verwandter Systeme I[J]. Mathematics and Statistics,1931,38(1):173-198.2 CSNB解壓
2.1 創建決策樹
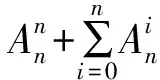
2.2 CSNB解壓算法
3 系統測試及結果分析
3.1 解的唯一性正向檢驗
3.2 解的唯一性反向檢驗

4 結束語

