內燃機KVMD MHD振動譜圖表征與TD 2DPCA編碼診斷方法研究

岳應娟 孫鋼 蔡艷平 王旭 牟偉杰

摘要： 為了直接對內燃機振動譜圖像進行診斷識別，提出一種基于改進變分模態分解（VMD）、MargenauHill（MHD）時頻分析與雙向二維主成分分析（Twodirectional， Twodimensional PCA，TD2DPCA）的內燃機振動譜圖像識別診斷方法。該方法首先針對VMD分解過程中的層數選取問題，提出了一種中心頻率篩選的VMD分解層數改進方法（KVMD），然后將內燃機振動信號利用KVMD分解成一組單分量模態信號，并對生成的各個單分量信號進行MHD處理后表征成振動譜圖像；在此基礎上，對生成的內燃機KVMDMHD振動譜圖像采用雙向二維主成分分析形成編碼矩陣，并采用最近鄰分類器（KNNC）對上述編碼矩陣直接進行模式識別，以實現內燃機振動譜圖像的自動診斷。最后，將該方法應用在氣閥機構4種工況下的缸蓋表面振動信號診斷實例中，結果表明：該方法不僅改進了傳統圖像模式識別中的特征參數提取方法，而且能很好地消除時頻分布中的交叉干擾項，使各時頻分量物理意義明確，能有效診斷出內燃機氣閥機構故障，為內燃機振動診斷探索了一條新途徑。關鍵詞： 故障診斷； 內燃機； 時頻分布； 特征提取； 雙向二維主成分分析

中圖分類號： TH165+.3； TK428文獻標志碼：A文章編號：10044523（2017）04068809

DOI：10.16385/j.cnki.issn.10044523.2017.04.021

引言

內燃機缸蓋振動信號中包含著豐富的信息，由于其測量的簡單方便，分析診斷的不解體和實時性，目前一直是內燃機故障診斷和狀態監測的研究前沿和熱點。國內外學者針對內燃機的振動響應信號進行了深入的研究，如文獻[1]將圖像分割理論引入柴油機故障診斷中，提出一種基于時頻譜圖、圖像分割和模糊模式識別的柴油機故障診斷方法；文獻[2]提出一種基于局部均值分解邊際譜和馬氏距離的故障診斷方法；文獻[3]將極坐標應用于柴油機燃燒狀態的監測，有效地提取了柴油機燃燒特征；文獻[4]將高階累積量與圖像紋理特征提取方法相結合，有效提取了柴油機振動信號的故障特征。

根據內燃機的構造和工作機理，氣閥與氣閥座會發生周期性的沖擊作用，若氣閥機構有故障， 其故障信息必然會在缸蓋振動信號中反映出來[56]。然而內燃機特征信號相互重疊和混淆、特征頻率難以確定，還沒有形成一個“針對不同故障，采用何種時頻分析方法，如何提取特征參數”的共識。究其原因是內燃機振動響應信號十分復雜，既有旋轉運動，又有往復運動，且運動部件多，耦合比較嚴重，具有較強的非線性、非平穩時變等特征[7]。

為有效解決內燃機振動響應信號強耦合、弱故障特征信息提取難題，提出了一種基于改進VMD（KVMD）的MHD時頻振動譜圖生成，TD2DPCA圖像特征參數提取的內燃機故障診斷新方法。KVMDMHD時頻分析法有效抑制了MHD分布中的交叉干擾項，并保留了其優良的時頻聚集特性，能夠準確刻畫出內燃機振動信號的時頻信息，使各時頻分量具有實際物理意義。對生成的KVMDMHD振動譜圖，直接采用TD2DPCA提取特征參數的方法，避免了在利用圖像分析技術進行特征參數提取時，不同圖像特征指標的選擇或只是提取圖像的單一特征量作為特征參數造成的重要的時頻信息遺漏，可對不同的圖像自適應地計算圖像的特征參數，數據降維效果明顯。

最后使用文中方法對內燃機氣門間隙的4種工況信號進行了分析和特征參數提取，結合最近鄰分類器（KNNC）進行故障診斷分類，并與基于MHD時頻分析的二維非負矩陣分解（2DNMF）和雙向二維線性判別分析方法（TD2DLDA）特征提取算法進行了對比。

1基于改進變分模態分解的MHD時頻分布〖*2〗1.1改進的變分模態分解（KVMD）變分模態分解（Variational Mode Decomposition，VMD）是2014年由Dragomiretskiy等提出的一種新的自適應信號處理方法[8]。對信號進行VMD分解時首先預設分解層數K，信號經過VMD被分解成K個本征模態分量（IMF），每個IMF都可以表示為一個調幅調頻uk（t）信號。因此K值選取的恰當與否，直接決定了分解結果的好壞。K值選取過小，對信號的分解不徹底；K值選取過大，會出現過分解現象。經研究發現每個IMF都存在著一個中心頻率ωk（t），K值與ωk（t）有著密切的關系，因此本文對通過中心頻率對分解層數K進行了優化。

第4期岳應娟，等： 內燃機KVMDMHD振動譜圖表征與TD2DPCA編碼診斷方法研究振 動 工 程 學 報第30卷KVMD算法的主要步驟為：

Step1初始化K值（K≥2，由于內燃機頻帶較寬，取K=3）。

Step2對信號進行VMD分解，得到K個IMF分量和每個IMF分量的中心頻率ωk（t）。

Step3用前一個IMFk-1分量的中心頻率ωk-1（t）比上后一個IMFk分量的中心頻率ωk（t），得到一組頻率比值λ1，λ2，…，λK-1（λk=ωk+1/ωk，k=1，2，…，K-1）。

Step4設定過分解閾值θ（根據內燃機頻帶特點取θ=1.1）。當λk>θ時，認為VMD分解不徹底，令K=K+1，重復Step2～Step3。

Step5當λk≤θ時可判定為IMFk和IMFk+1頻率混疊，VMD出現了過分解，因此得出結果K=K-1，并輸出其分解結果。

1.2基于改進變分模態分解的MHD時頻分布

MHD時頻分布[9]是一種非平穩信號分析的工具，具有真邊緣性、弱支撐性、平移不變性等優良性質。對給定信號x（t）的時頻分布p（t，f），Cohen給出一般形式的表達式p（t，f）=∫+∞-∞∫+∞-∞∫+∞-∞xu+τ2x*u-τ2·

τ，ve-j2π（tv+τf-uv）dudtdv（1）式中τ，v是核函數。若≡0，則為WignerVille分布，當=cos（πτv）時，即為MHD分布pMH（t，f）=∫+∞-∞∫+∞-∞∫+∞-∞xu+τ2x*u-τ2·

cos（πτv）e-j2（tv+τf-uv）dudτdv（2）由于雙線性核函數的引入，使多個分量在時頻平面發生耦合產生了交叉項，MHD時頻分布很難將有多個頻率成分的信號表示清楚[10]。MHD分布的交叉項是以兩個自項構成的矩形對角線頂點，若兩個自項分布位于同一頻率或同一時間時 ，則自項和交叉項重疊。若對MHD進行加窗處理，就得到了偽魏格納分布（PMHD）。pPMH（t，f）=∫+∞-∞∫+∞-∞∫+∞-∞h（τ）xu+τ2x*u-τ2·

cos（πτv）e-j2（tv+τf-uv）dudτdv（3）式中h（τ）為窗函數。

信號x（t）的KVMDMHD時頻分布定義為KVMDMHDt，f=∑Ki=1∫∞-∞fMHDIMFit，fdfMHDIMFit，fdf（4）KVMDMHD時頻分布是利用了線性時頻表示滿足疊加原理的思想[11]。為消除交叉干擾項，可以將待分析的信號經KVMD分解成一組單分量信號IMF1，IMF2，…，IMFK，先對各個單頻率分量信號單獨進行MHD分析，這樣在頻域上就不會產生交叉干擾項，而位于同一頻率的時域交叉項會與自項相互疊加，對自項有增強作用，對信號的分析有積極的作用；再將結果線性疊加，這樣在保留了MHD時頻分布的優良特性的同時，有效地消除了MHD的交叉項的干擾。

為分析該方法的性能，建立一個多分量仿真信號， 設x（t）是由3個原子復合而成，他們的位置分別位于（t1，Ω1）=（28，0.1），（t2，Ω2）=（28，0.4），（t4，Ω4）=（100，0.4），該信號的時域和頻域波形如圖1所示。

圖1仿真信號

Fig.1Simulation Signal圖2給出了仿真信號的MHD時頻分布圖，圖中顏色表示信號在對應的時間和頻率處的能量幅值大小與圖像右側的顏色標尺對應。僅從時頻相平面圖中已經很難分辨哪個是自項，那個是交叉項，通過對原始信號進行分析和比對，可以發現在（t2，Ω2）=（100，0.1）為交叉項，其余均為自項與交叉項的疊加。

圖2MHD時頻分布圖

Fig.2Timefrequency distribution of MHD圖3PMHD時頻分布圖

Fig.3Timefrequency distribution of PMHD

對MHD做加窗處理得到x（t）的PMHD分布圖如圖3所示。從圖3可看出，這時交叉項得到抑制，但丟失了自項信號的一些細節，犧牲了時頻分辨率，使生成的時頻譜圖不便于分析和理解。

對x（t）使用文中方法進行分析處理得到KVMDMHD的時頻分布圖。如圖4所示，KVMDMHD時頻分析已經去除了交叉項的干擾，使自項分辨的很清楚。

圖5所示為2原子和4原子的仿真信號，及其MHD和KVMDMHD時頻分布圖。從圖中可以看出，2原子信號的MHD時頻分布在對角構成矩形的另一對角上存在交叉干擾項，圖4KVMDMHD時頻分布圖

Fig.4Timefrequency distribution of KVMDMHD

4原子信號的MHD時頻分布圖為自項與干擾項的疊加；而兩者的KVMDMHD時頻分布圖均能有效消除MHD分布中的交叉項的干擾。

圖5多原子信號時頻分布圖

Fig.5Timefrequency distribution of multiatoms2TD2DPCA分解

傳統的PCA方法需要將二維矩陣數據向量化，樣本維數比較大，計算效率低下。2DPCA在特征提取上是直接利用二維投影的方法，數據量少，在提取特征上耗時也更少。但2DPCA僅在圖像的行方向上進行運算，忽視了圖像列中包含的信息，TD2DPCA[1213]將行和列兩種圖像信息融合到一個判別分析框架中，識別率得到提高，同時計算復雜度較低。

假設有C類模式：ω1，ω2，…，ωc，總共M個訓練樣本圖像：A1，A2，…，AM，每個大小為m×n。Gt為訓練樣本總體散度矩陣Gt=1M∑Mi=1Ai-TAi-（5）式中=1M∑Mi=1Ai為訓練樣本的均值矩陣，可證Gt是n×n的非負定矩陣。

通過線性變換將圖像矩陣Ai投影至X上從而獲得特征向量Y=AiX（i=1，2，…，k），其中X表示n維單位化的列向量。投影方向X的選取準則是使得投影后的特征向量具有更好的可分性。定義準則函數J（X）=tr（Gt）=XTGtX（6）式中tr（Gt）為Gt的跡。

為了實現投影后得到的特征向量總體分散程度最大，即J（X）最大，需要尋找最優投影向量X。其實，Gt的最大特征值所對應的單位特征向量即為最優投影向量。因Gt為非負定矩陣，則有n個標準正交的特征向量，假定GtXi=λXi，（λ1≥λ2≥…≥λn≥0）（7）為了提高在多類樣本情況下的區分性，單一的最優投影方向是不夠的，取前d個最大特征值所對應的標準正交的特征向量作為最優投影矩陣P。假設P=[X1，X2，…，Xd]。對圖像樣本A，利用最優投影矩陣對其進行特征提取，獲得相應的特征編碼矩陣B，即B=AP。

對第1次提取的特征Bi（i=1，2，…，M）作為訓練矩陣進行第2次特征提取，即將BTi作為Ai代入式（5），得到新的散布矩陣t=1M∑Mi=1Bi-Bi-T（8）式中=1M∑Mi=1Bi為首次提取特征后訓練集的均值矩陣。

構造與式（6）相似的準則函數，求解t的前h個最大特征值所對應的標準正交的特征向量Z1，Z2，…，Zh，以此作為第2次特征提取的最優投影矩陣Q，則任一圖像A經TD2DPCA算法提取的特征矩陣U為U=BT[Z1，Z2，…，Zh]=PTATQ=

[X1，X2，…，Xd]TAT[Z1，Z2，…，Zh]（9）特征矩陣U的維數為h×d，相比于2DPCA第1次提取出的特征維數為m×d，h遠小于m，從而進一步壓縮特征維數，提高了后續分類效率。

3內燃機故障診斷實例〖*2〗3.1內燃機智能故障診斷流程基于KVMDMHD與TD2DPCA的故障診斷方法對內燃機的故障診斷，共分為以下幾個步驟：首先對采集到的內燃機振動信號進行KVMDMHD時頻分析得到時頻分布圖像，然后采用TD2DPCA對時頻圖像進行分解得到圖像的特征參數，最后用分類器對特征參數進行分類，完成對內燃機的故障診斷，具體方法的步驟如圖6所示。

圖6基于KVMDMHD與TD2DPCA的故障診斷方法的步驟

Fig.6Fault diagnosis method based KVMDMHD and TD2DPCA3.2內燃機實驗工況

文中以6135型柴油機為研究對象，實驗平臺由柴油機、傳動軸、電機和控制臺4部分組成，如圖7所示。取內燃機第2缸蓋表面振動信號對內燃機進行故障診斷，采樣頻率25 kHz，轉速為1500 r/min，測試過程中，內燃機空載運行。共設置了4種氣門間隙狀況，具體情況如表1所示。其中0.06，0.3和0.5 mm分別對應排氣閥氣門間隙過小、正常與過大，開口表示在氣閥上開4 mm（長）×1 mm（寬）的口來模擬嚴重漏氣。實驗共采集內燃機氣門4種工況（3種故障狀態和1種正常狀態）下各60種振動信號樣本，總計240個。

圖7試驗平臺

Fig.7Experimental platform表14種實驗工況設置（單位：mm）

Tab.1Four states of IC engines valve train（Unit：mm）

狀態編號進氣門排氣門10.300.3020.300.0630.300.5040.30開口4×13.3內燃機缸蓋振動信號的KVMDPMHD時頻分析根據6135柴油機的工作原理可知，引起缸蓋振動的原因主要是本缸氣體燃燒時產生的爆壓、本缸氣閥落座撞擊以及排氣門開啟所引起的氣流沖擊等，其次鄰缸的各種振動激勵源也會對缸蓋的振動產生較大影響[14]。圖8所示為進排氣閥開閉與曲軸轉角的關系。進氣門開啟的角度在排氣上止點前20°附近，關閉的角度在進氣下止點后48°附近；排氣門開啟的角度的在做功下止點前48°附近，關閉的角度在排氣上止點后20°附近；柴油機在0°點火。

圖8內燃機燃燒和氣閥開閉轉角圖

Fig.8Angular distribution of vibroimpact events from valve train and combustion

對正常工況信號進行VMD分解，不同K值下的中心頻率如表2所示。表2不同K值對應的中心頻率（單位：Hz）

Tab.2Center frequency corresponding to different K（Unit：Hz）

K=2K=3K=4K=51456130412847767678447744661783—768574644473——81177464———8117

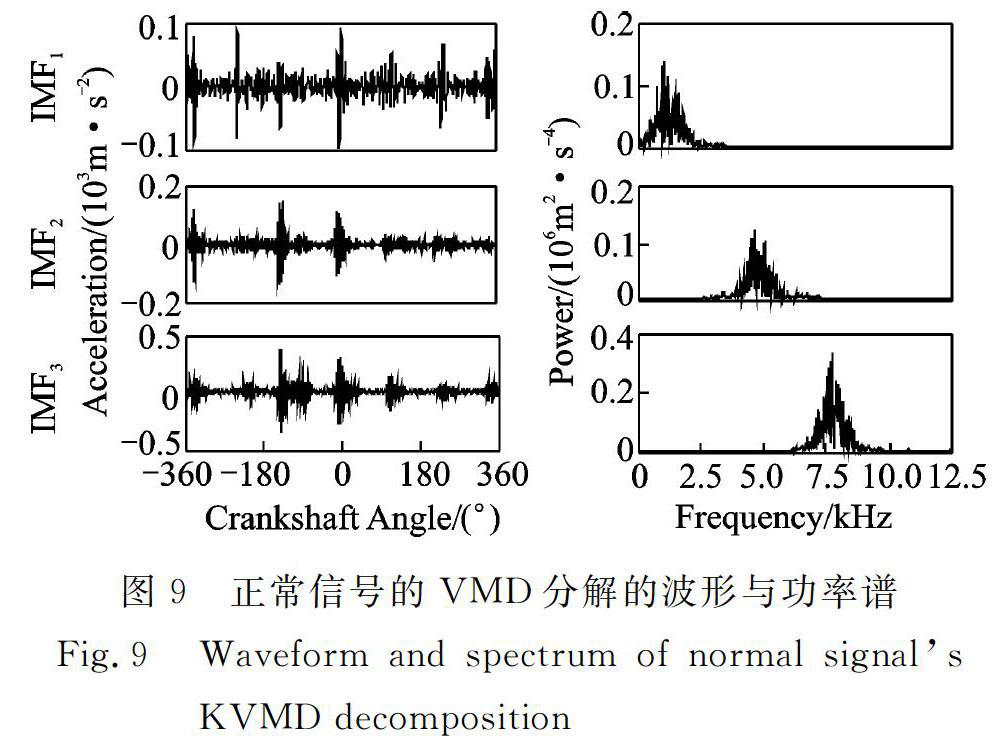
對于正常工況，當K值為4和5時，中心頻率出現了比較相近的7464 Hz和8117 Hz，這兩個中心頻率相近8117/7464=1.08，1.08小于過分解閾值θ，認為出現了過分解現象，因此K應取分解層數4的上一層，即分解層數K=3。圖9所示為正常工況信號經KVMD分解后的波形及其功率譜圖。

圖9正常信號的VMD分解的波形與功率譜

Fig.9Waveform and spectrum of normal signals KVMD decomposition

氣閥正常工況下的缸蓋信號通過KVMD分解得到的中心頻率為1304，4477和7685 Hz，與文獻[15]中所述內燃機缸蓋振動信號的頻域特性“進氣門開啟和閉合時產生的振動響應相似，其能量主要集中在6～8 kHz；排氣門開啟和關閉時產生的振動響應相似，其能量主要集中在6.5～8 kHz；燃燒產生的振動能量主要集中在4～6 kHz，燃燒后段產生的振動能量主要集中在0.8～1.7 kHz”相一致。中心頻率1304，4477和7685 Hz分別與燃燒后段、燃燒和進排氣門開啟和關閉的能量相對應，充分驗證了過分解閾值θ=1.1的有效性。按照上述方法分別對氣門間隙過小，氣門間隙過大和氣門漏氣工況進行分析，大量的實驗結果表明KVMD方法對信號的剖分適當，有利于對信號的進一步分析研究。

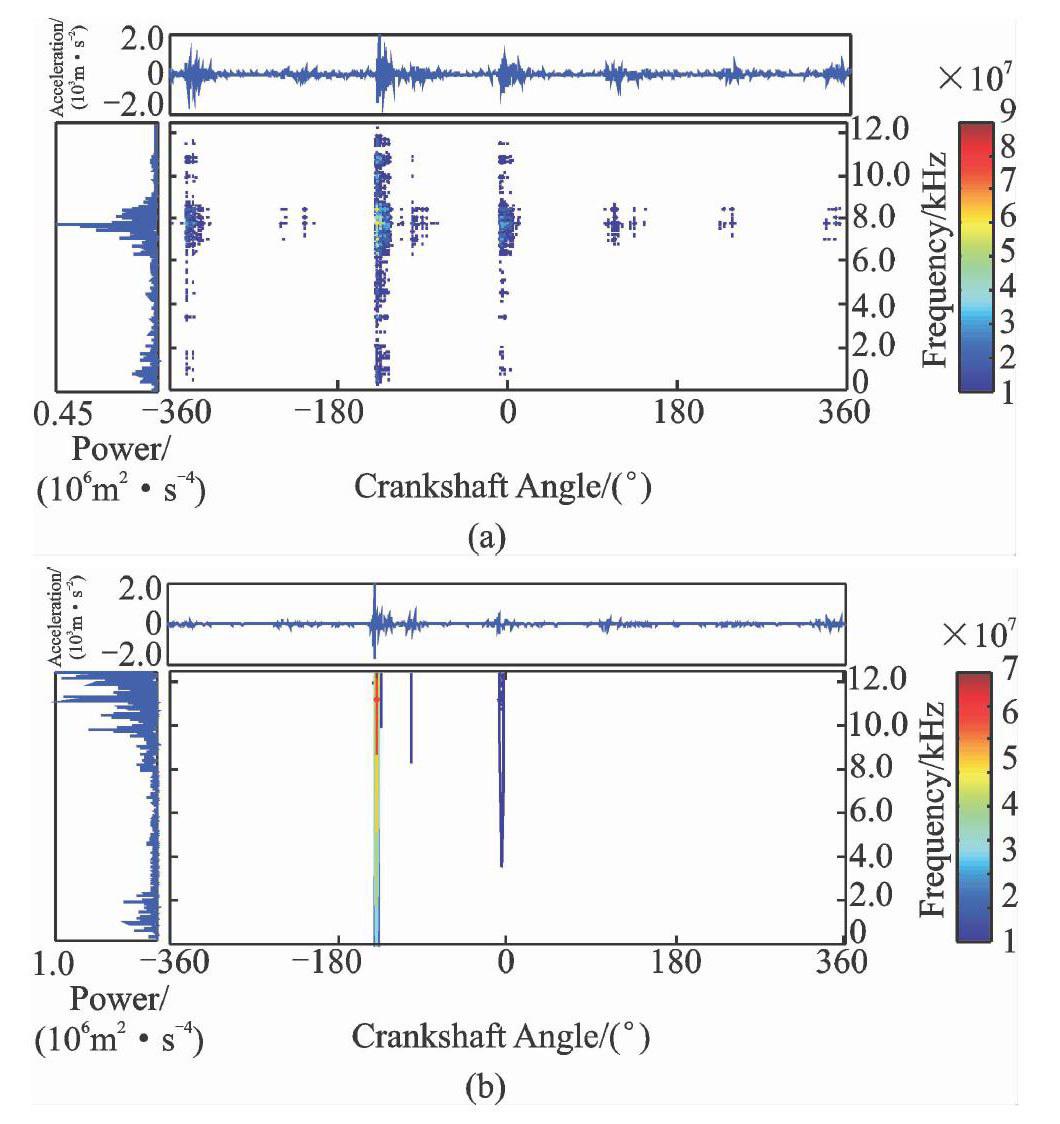
分別繪制缸蓋表面振動信號MHD時頻分布圖和KVMDMHD時頻分布圖，如圖10和11所示，每幅圖中從上至下依次為氣門間隙正常、過小、過大和漏氣4種工況。圖中最上方的曲線為信號的時域波形圖，橫坐標表示時間，縱坐標表示幅值；左邊的曲線為信號的功率譜圖，橫坐標表示頻率，縱坐標表示幅值（將功率譜圖順時針旋轉90°看）；中間的圖像為時頻相平面圖，橫坐標表示時間，縱坐標表示頻率；圖中的顏色代表能量幅值的大小，與右邊顏色標尺圖對應。

圖10振動信號的MHD時頻圖

Fig.10MHD timefrequency image of vibration signal圖11振動信號的KVMDMHD時頻圖

Fig.11KVMDMHD timefrequency image of vibration signal

從圖中可以發現缸蓋表面的振動信號具有時變和非平穩的特性，隨氣門間隙的變化各個工況的時頻相平面圖呈現出較大差異，沖擊分量信息在時頻相平面圖上出現和消失時間不同，幅值大小不同，并且它們頻率組成更不相同。對比圖10和11可得，圖10用MHD方法對缸蓋振動信號進行時頻分析時頻域上存在嚴重的交叉干擾項，只能分辨出較大沖擊位于曲軸轉角的位置，無法表示該位置存在的具體頻率，造成頻域信息丟失，增加了故障診斷難度。圖11中KVMDMHD方法可以有效地抑制MHD方法中的交叉干擾項，清晰地分辨出各較大振幅處存在的頻率分量，具有良好的時頻聚集特性，更有利于后續特征提取與分類。

從能量的分布的角度來看：圖11中可以看出，圖（a）氣門間隙正常時缸蓋振動信號的能量主要集中在7～8.5 kHz之間的頻帶；圖（b），（c），（d）當氣門間隙處于故障狀態時，主要能量會集中在9～12 kHz高頻區，相比于正常工況，主要能量分布有向高頻移動的趨勢。

從燃燒做功的角度來看：氣缸內的混合可燃氣體做功與否或是否充分燃燒，其特征信息必然會在曲軸轉角0°附近體現。圖11（a）中，氣閥間隙正常時，內燃機正常工作，缸內氣體燃燒正常，其對應的沖擊分量十分明顯。但這一振動分量在圖11（b），（c），（d）中很不明顯，這說明氣門間隙異常（過大或過小）對柴油機的燃燒影響比較大。因為排氣閥氣門間隙過小或漏氣，就會引起氣門密封不嚴，產生漏氣；過大，則將使氣門遲開、早關，排氣時間縮短，影響混合氣體的更新，影響正常燃燒。

從振動分量分布的角度來看：4種工況的進氣閥都正常，所以進氣閥落座產生的沖擊分量在4幅圖中曲軸轉角-132°附近位置均得以體現。圖11（a）中排氣閥處于正常狀態，所以其位置對應于在曲軸轉角-340°附近和頻率為7.8 kHz附近；圖11（b）中，排氣閥氣門間隙過小，因此沖擊分量在圖中表現的不是很明顯；圖11（c）和圖11（d）中排氣閥處于氣門間隙過大和漏氣狀態，因此頻率區別于正常工況的7～8.5 kHz，遷移至高頻部分9～12 kHz。曲軸轉角為132°和340°附近時，排氣閥和進氣閥先后開啟，由于氣閥開啟時引起的沖擊相比于氣閥關閉或是燃燒引起的沖擊要小的多，因此在時頻分布圖中體現的并不是很明顯。

3.4KVMDMHD時頻譜的TD2DPCA特征提取

取采集到的240個信號作為研究對象并分別繪制KVMDMHD時頻相平面圖，相應得到240個300×400像素點的時頻矩陣。由于得到時頻矩陣維數高，計算量大，不利于進行特征參數的提取，對圖像進行預處理，將其轉化為灰度圖像。

KVMDMHD時頻相平面圖的局部非負矩陣特征參數提取流程如下：

Step 1從4類工況時頻分布圖中每一類隨機選取30幅共120幅，組成TD2DPCA樣本集T；

Step 2對樣本集T進行TD2DPCA特征提取，最優投影矩陣P300×d和Q400×h。d和h分別表示兩次提取的特征維數，它的取值對特征提取結果和后續的識別精度有較大影響；

Step 3將所有時頻相平面圖向矩陣P和Q投影，可得其對應得編碼系數矩陣H，H的維數為h×d，每一個編碼系數矩陣H代表了它所對應的時頻相平面圖。

圖12給出的是特征維數h×d=5×5時，KVMDMHD時頻相平面圖訓練集對應的特征系數，圖中每個像素所對應的色柱值嚴格與樣本的編碼系數值保持一致，文章篇幅有限，每種工況下選取5圖12TD2DPCA提取的測試集特征系數

Fig.12Test set parameters for TD2DPCA

個樣本的編碼系數矩陣進行顯示。圖中每一行代表一種內燃機工況，從上到下依次為氣門間隙正常、過小、過大和漏氣。可以看出TD2DPCA對數據進行了非常有效的降維，將300×400維數據壓縮到5×5維，大大降低了識別復雜度和計算量。從圖中可以看出，同種工況樣本的編碼矩陣系數較為相似，不同工況間編碼矩陣系數區別較大，這有利于后續參數的分類識別。

3.5故障識別

在對內燃機氣門間隙工況進行分類時，選擇最近鄰分類器（KNNC）作為內燃機運行工況判別的智能學習機器。從4類工況中每一類中隨機選出30個編碼矩陣H共120個，組成訓練樣本集合。然后用剩余的120個系數向量作為測試集合進行分類測試，重復以上實驗10次取平均值。用識別正確率為指標來評價文中方法的性能。為進行對比分析，分別采用雙向二維主成分分析（TD2DPCA）、雙向二維線性判別分析方法（TD2DLDA）和二維非負矩陣分解（2DNMF）算法對生成的MHD和KVMDMHD時頻分布圖像進行特征提取并分類。由于在上述特征提取方法對時頻分布圖進行特征提取過程中涉及特征維數對識別準確率的影響，為增強3種方法的對比性，保持編碼矩陣維數的一致性，令2次提取的特征維數d×h=r×r=[2×2，3×3，…，10×10]，識別率準確率結果如圖13所示。

圖13三種特征提取方法的識別率

Fig.13Recognition rate of three feature extraction methods從圖13（a）中可以看出，使用3種分類方法對MHD時頻分布圖進行特征提取，其中TD2DLDA的識別率相對較低，在不同的特征維數下識別準確率平均值低于85%；TD2DPCA和2DNMF的識別準確率相差不大，各個特征維度的識別準確率都在90%以上，但在試驗過程中，由于2DNMF在特征提取過程中要將所有訓練數據矩陣按行和列進行拼合，初始分解矩陣維數較大，迭代過程效率低，計算耗時較長。圖13（b）中，3種分類方法對KVMDMHD時頻分布圖進行特征提取，識別率與圖13（a）中相比，3種方法均有較大提高。這是由于采用KVMDMHD對內燃機振動信號進行時頻分析時，生成的時頻分布圖時頻聚集性好，各個工況間的差異更明顯，更利于分類器的分類。TD2DPCA在特征矩陣維度為5×5和更高維度時，識別準確率高達100%。對比圖13（a）和（b），表明采用基于KVMDMHD與TD2DPCA的故障診斷方法適用于內燃機氣門間隙的故障診斷，并具有較高的診斷精度。

4結論

1） 優化了VMD分解中K值，增強了分解的自適應性，將其與MHD時頻分析法相結合，提出了KVMDMHD時頻分布，該方法有效抑制了MHD分布中存在的交叉干擾項，具有很高的時頻分辨率。用該方法對不同氣門間隙工況進行分析，各工況的時頻分布特征明顯，時頻分量物理意義明確。