基于VaR若干模型對于股指期貨風險測度的研究與比較
文/岳乾良
基于VaR若干模型對于股指期貨風險測度的研究與比較
文/岳乾良
上海大學
目前VaR的度量方法有很多,而且各種方法計算出的VaR值可能相差很大,,針對這一點本文基于滬深300股指期貨為研究對象,比較檢驗了擊中典型的風險度量方法,對蒙特卡洛模擬法,GARCH法和歷史模擬法三種方法逐一進行介紹,并對上述模型采用kupic失敗檢驗法進行后驗測試,以比較模型的準確度,得出在當今運用比較廣泛的幾種VaR模型中,哪個是最可行和有效的
VaR模型;滬深300股指期貨;模型后驗
1 引言
VaR(Value at risk)模型作為一種測量市場風險的方法,具體含義是指在一定置信水平和一定持有期內,某一金融工具或其組合在未來資產價格波動下所面臨的最大損失額。自 1993 年被JP Morgan 公司首先使用以來,很快被國際上的金融機構廣泛采用。
那么,用 VaR 模型來測量滬深 300 指數的市場風險是否可行呢?要用VaR模型來測量市場風險,就涉及到計算方法的選擇,模型參數的確定等,而這些問題VaR模型本身是給不出答案的。這些問題只有通過采用不同的方法估計VaR,進行檢驗,才能觀察哪一種模型能有效測量滬深300指數的市場風險。
2 數據來源及描述性統計
本文選取的數據為滬深300股指期貨2013年1月4號至2017年二月17號的日收盤價,共1000個數據,選取一天為持有期,置信水平為95%數據均來源于Wind數據庫。用一階差分來代表收益率,用表示滬深300指數交易日t的對數收益率,為交易日的日收盤價,為前一天日收盤價,那么以下是描述性統計量。隔夜收益最大值和最小值分別為6%和-9%,由于我國股指期貨采用10%的保證金比例交易,那么杠桿化后的隔夜收益變動將進一步放大,這充分說明了股指期貨潛在隔夜風險不容忽視具有研究的價值意義,偏度系數和超額峰度系數均在5%水平下顯著,說明隔夜收益序列具有右偏和“尖峰厚尾”的性質。J-B統計量和QQ圖的結果顯示收益率具有明顯的非正態性質,ADF單位根檢驗結果顯示日收益率是不具有長記憶的的平穩序列。
3 VaR模型及其結果
3.1歷史模擬法
作為一種非參數風險管理模型,歷史模擬模型不對股價指數資產組合收益率分布的具體形態作任何假定,而是僅以歷史收益率可以在未來重復自身為假設前提,即在每一樣本期間內資產組合收益率服從相同的獨立分布,從而可以根據歷史樣本期間內股價指數資產組合收益率的頻率分布來估計資產組合未來時期內的VaR值
3.2Monte Carlo method
蒙特卡羅是根據市場數據的歷史波動用計算機模擬出市場因子的未來波動的大量可能路徑,由于具有高度的靈活性,很多銀行機構,例如信托公司、BZW 等都采用蒙特卡羅模擬技術。隨著計算機功能日漸提升,這種方法也越來越受到歡迎。
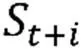
重復上一步驟m次,可以計算出m次條件下的目標時刻T的價格序列L= { S1T,S2T,…SiT,…SmT }。其中 m值越大,重復次數越多,則隨機生成并計算出的目標時刻價格序列涵蓋的可能性越多,也更加接近現實情況.
3.3GARCH模型
由于金融資產價格的變化往往呈現聚集性的特征,對參數估計造成了干擾。而 GARCH 族模型能夠更好的刻畫金融資產的波動性,可以更好的來估計VaR的參數。廣義自回條件異方差GARCH模型是在1982年由Engle引入的,由Bollerslev于1986年提出來的
GARCH-VaR模型:
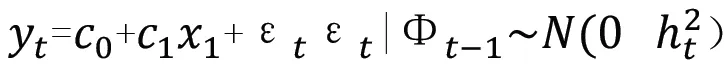
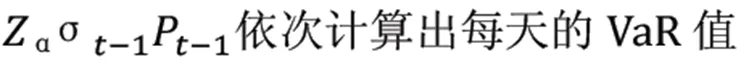
4 模型的后驗方法和結果分析
為了檢驗上述各模型的樣本動態VaR預測效果,kupic提出了一種VaR失敗率的似然比檢驗方法,為了進行該檢驗,首先定義擊中序列(Hit Sequence),以多頭VaR為例,定義如下:
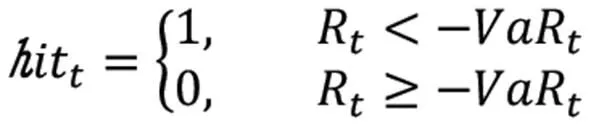
它表示的是,如果t時刻的實際收益超出所估計的VaR值,稱為一次擊中事件,那么該序列t時刻的取值為1,否則為0。假設該模型能有效地預測隔夜風險,則該“擊中序列”應服從貝努利分布。
在模型沒有誤設的零假設下,構造似然比的非條件檢驗統計量;

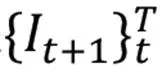
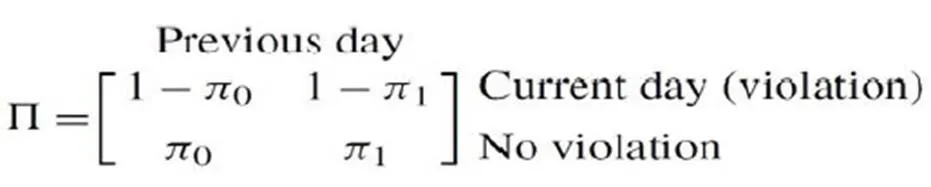
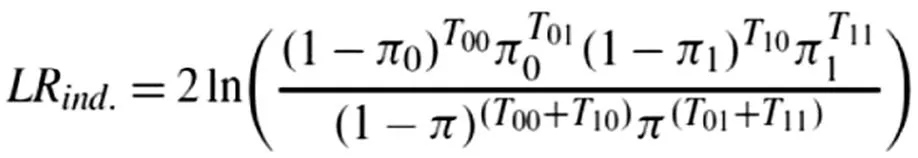
其中,p為顯著性水平,N為預測的樣本總數,n為預測樣本中的失敗次數。通過上式可知道Kupic檢驗量是刻畫實際失敗次數近理論失敗次數程度的指標。當LR統計量大于給定置信水平下卡方分布的臨界值,則拒絕原模型。相反,當統計量小于臨界值,則接受該模型,下表為各模型LR檢驗值。
從檢驗值的結果來看,蒙特卡洛法要比GARCH法在接受模型上更有說服力,兩者均小于臨界值,未拒絕模型。但是,Kupic似然比檢驗只是檢驗實際擊中比與理論擊中比率的接近度。進一步的研究表除了檢驗失敗比率以外,還應檢驗失敗值間是否存在相關性,如果發生VaR預測失敗觀測值之間具有明顯的相關性,那么有可能發生續超過VaR 的損失,這將給投資者帶來巨大的損,也就是說,精確可靠的風險測度模型的擊中序列,應該是無偏和無自相關的。
5 總結
對于四年的數據95%的置信度下,預期觀測到的失敗個數理論上應5%×1000=50,但是只要N在區間(37,65)內,就不能拒絕零假設,歷史模擬法和VaR-GARCH法的失敗次數均未落在了區間內,且明顯大于65,這說明歷史模擬法和garch法都低估了風險水平,只有蒙特卡洛方法落在了區間內,但是對于蒙特卡洛模型高估了損失發生的概率,其模型過于保守,,從失敗檢驗法檢驗值知,蒙特卡洛方法中擊中次數更為接近理論值,三個模型中只有蒙特卡洛通過了檢驗。從獨立性檢驗來看,歷史模擬法拒絕了原假設,其在集中序列的獨立性上表現不太好,蒙特卡洛和garch模型均為拒絕原假設,就上述模型來講,針對這組數據,顯然蒙特卡洛方法更勝一籌。

