第二十四講 混料組合均勻設計
徐靜安 段敏偉
2014年的8月19日是地球超載日。楊維成、段敏偉來我辦公室討論甲醇柴油微乳化混料試驗方案,涉及DPS數據處理系統,我的電腦中存有蛇年(2013年)張玉梅給我下載的電子版。兩位青年同仁得知我眼睛老花加散光閱讀電子版較累,提出把紙質版的書送給我,因他們更需要學習而被我婉拒。8月25日,段敏偉來我辦公室談及開發中心已訂購正版DPS軟件,附贈紙質版的新版《DPS數據處理系統——實驗設計、統計分析及數據挖掘》(唐啟義著),所以代表羅勇、楊維成把現有第2版的專著送給我,不會影響學習。喜得此書后,再一次瀏覽全書(1 138頁)。
序二同行評價DPS分析軟件“開發了具有全球領先地位的均勻試驗設計、混料試驗設計、動態聚類分析幾個功能模塊的獨創算法”。對此相應章節結合院內項目案例進行了精讀。
筆者在1987年12月6日于北京王府井購買的《試驗優化技術》一書中初次接觸“均勻設計”、“混料回歸設計”等。陳濤是上海化工研究院較早在阻燃劑技術開發中應用混料回歸設計中的“極端頂點設計”的,我還在他那兒借閱過《六西格瑪管理統計指南——MINITAB使用指導》,閱后于2008年我去上海書城購得,再讀,此后建議院部購買一批在科技人員中發放。
自2014年10月份以來,段敏偉平均十天半月討論一次混料試驗方案,期間閱讀了上述幾本書,并學習了其中的典型案例,對混料試驗設計的傳統方法、經典方法、混料均勻設計方法有所了解,有了和筆者合作、開發應用混料組合均勻設計方法的基礎。
一、有過程參數的混料均勻設計
在工程混料試驗中,往往涉及到混料配方反應的溫度、壓力、時間以及配方在基料中的添加量等這些過程參數(變量)。在不得已的情況下,過去采用固定這些過程參數來對混料配方試驗作出評價,實際上默認這些過程參數對混料配方的交互作用不作考慮,并認為考察范圍是單峰函數。如對一些重要的混料配方試驗,必須考察其交互作用,就采用優化試驗中的“轉軸法”思想,分段輪換考察:初定過程參數,考察混料配方——選定混料配方,考察完善過程參數——固定完善后的過程參數,優化混料配方。顯然實驗工作量是很大的,尤其是在多目標響應Y有多個技術指標約束時,數據的分析處理會帶來困難。所以實際研究工作往往是滿足于獲得“可用的配方”,不得已而為之。
把過程參數變量和混料配方組分組合在一起的均勻設計,就構筑成混料組合均勻設計。
現代應用數學方法叢書7之《正交與均勻試驗設計》(方開泰、馬長興著,科學出版社2001年出版),在“均勻設計應用的廣泛性”、“混合類型因素的試驗”中,提出基于均勻設計Un(nl)表構筑混料組合均勻設計的思想。
《DPS數據處理系統——實驗設計、統計分析及數據挖掘》(唐啟義著,科學出版社2010年出版)在“偏最小二乘回歸分析”混料試驗數據建模的案例中,展示了含過程變量的混料試驗的數據處理。
對于數理統計學家,混料組合均勻設計在學術上似乎已經解決,沒有進一步展開討論,但在工程界應用、構筑試驗設計方案時還存在一些不夠方便的“坎”,所以應用不夠廣泛。
二、混料組合均勻設計方案構筑
對于混料組合均勻設計,過程變量是獨立的,混料配方存在∑Xi=1的約束。所以如本刊2018年第二期刊登的第二十二講“混料均勻設計簡介”中敘述,需對均勻表中混料配方所占列進行逆變換。
現以1個過程變量,P=3可轉換成正單形的混料試驗為例,構筑設計方案。
本例考察的過程變量數C=1,配方變量數P-1=3-1=2,所以首先要選擇一個均勻設計表Un(n3)。
均勻設計一般要求試驗次數n≥2~2.5倍考察變量數,而經典的混料回歸設計試驗次數n≥3~5倍考察變量數。本案例取n=7,選用U7*(74)表,根據使用表,過程變量安排在第2列,將混料配方P-1=2分別安排在3,4列。具體見表1~2。
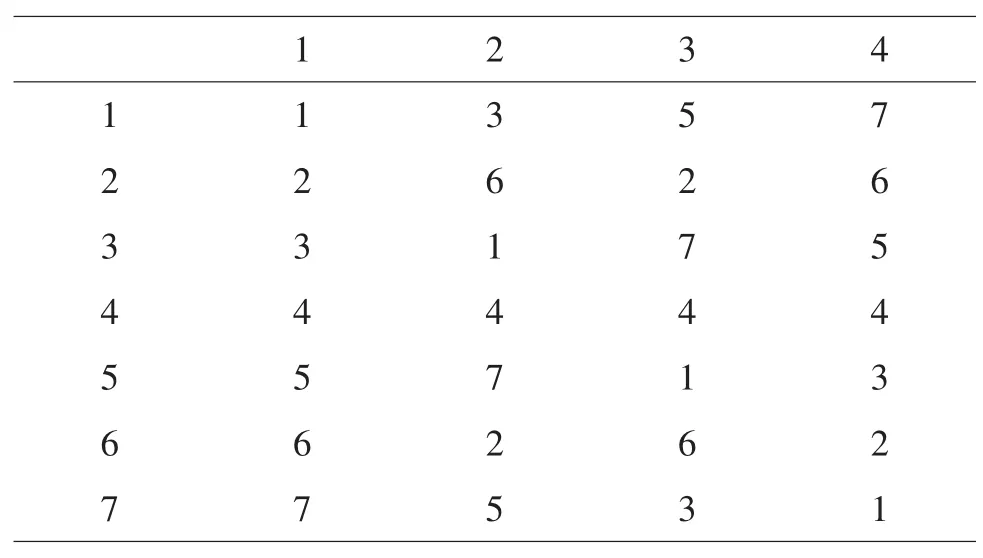
表1 U7*(74)

表2 U7*(74)的使用表
用{qji}表示所選均勻表第j列中的第i(i=1,2,…,n)個元素進行轉換。

將{Cji}轉換成{Xji}
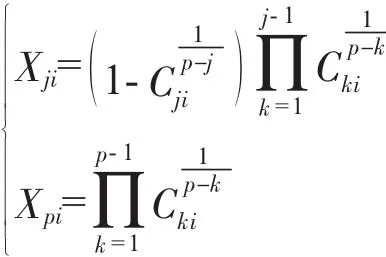
式中:Π為連乘符是Cji的次方數。
計算詳見本刊2018年第二期刊登的第二十二講“混料均勻設計簡介”。筆者為了加深對此變換的理解,本著“眼過千遍,不如手過一遍”的古訓,用手機上的計算器模塊作了逐項計算,構筑成表3。
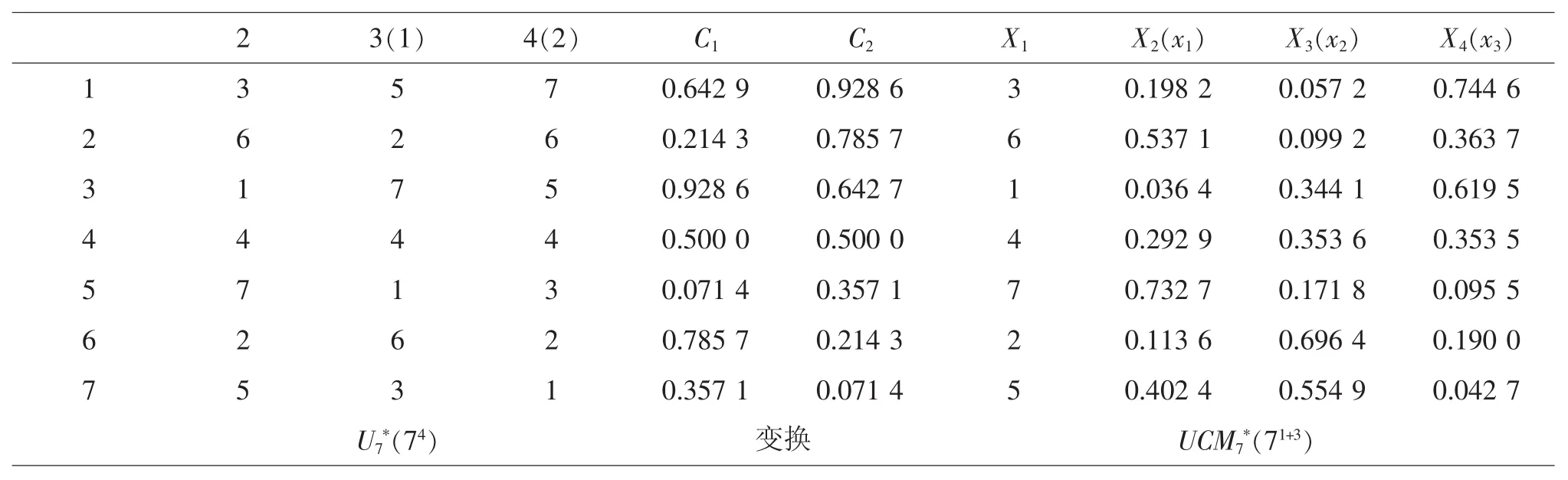
表3 用計算器模塊作逐項計算結果
在單純混料均勻設計中,介紹均勻設計U7*(74)表變換成UM7*(73)混料均勻表的過程。U表示均勻設計,M 為混料試驗,n=7(實驗次數),np=73,為P=3的三組分配方試驗。專著中沒有對混料組合均勻設計明確命名,筆者按此思路建議:
均勻設計U7*(74)表變換成混料組合均勻設計UCM7*(71+3)表,其中:C表示組合過程變量;nc+p=71+3,上角碼C表示組合的過程變量數,P表示配方的組分數。
在上表中,為了和UMn*(np)表對應,C1,C2變換成(x1)、(x2)、(x3),由于有過程變量,在UCM7*(71+3)中應為 X2,X3,X4。而統計建模時,通用方法僅 X1,X2,X3進入模型。
三、常用混料組合均勻設計表
為了便于應用,段敏偉通過DPS數據軟件對U7*(74)變換成UCM7*(71+3)等,詳細步驟如下:
在變換前,先將需要變換的U7*(74)表第3,4列輸入到DPS軟件的電子表格中,并按照圖1所示定義成數據塊。(備注:在DPS V14.50版本中,由于軟件存在缺陷,經與唐啟義老師溝通后,數據塊需要多選擇一列空列)。然后執行DPS“混料試驗設計”里面的“混料均勻設計”功能模塊即可得到如圖2所示的混料均勻設計。上述計算結果和筆者按方開泰提出的變換公式用手機計算器計算得到的結果一致,僅個別數據末位由于進位精度存在0.000 1的差異。常用混料組合均勻設計見表4~5。
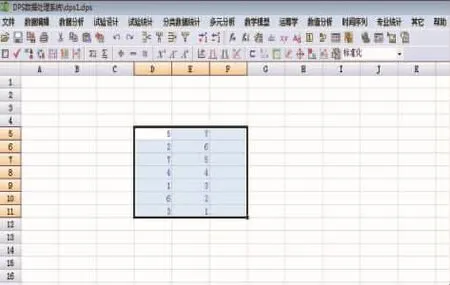
圖1 通過DPS數據軟件定義成數據塊
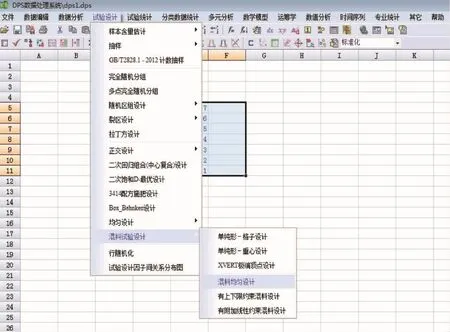
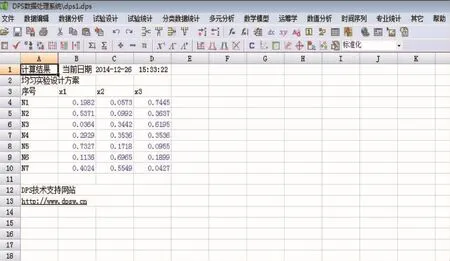
圖2 混料均勻設計
1 U10*(108)變換成UCM10*(101+3)
過程變量C=1、配方因素數P=3,查U10*(108)的使用表,選擇第1,5,6列,過程變量安排在第1列,將混料配方P-1=2分別安排在第5,6列。對第5,6列采用DPS軟件及上述步驟進行變換,從而得到了UCM10*(101+3)表(見表6)。
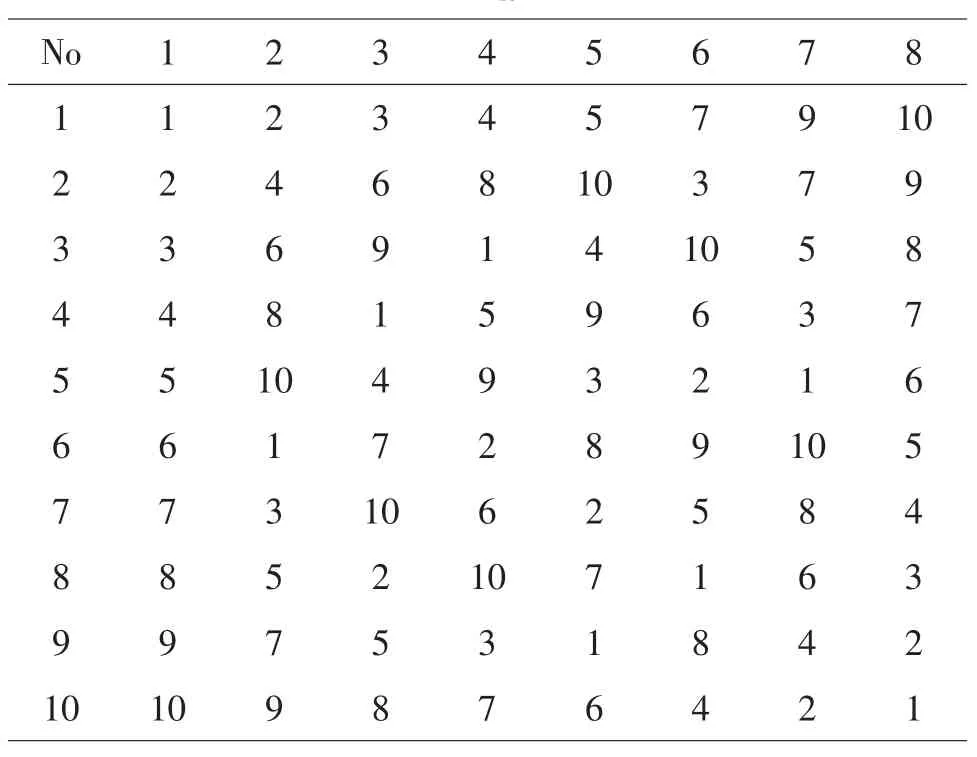
表4 U10*(108)

表5 U10*(108)的使用表
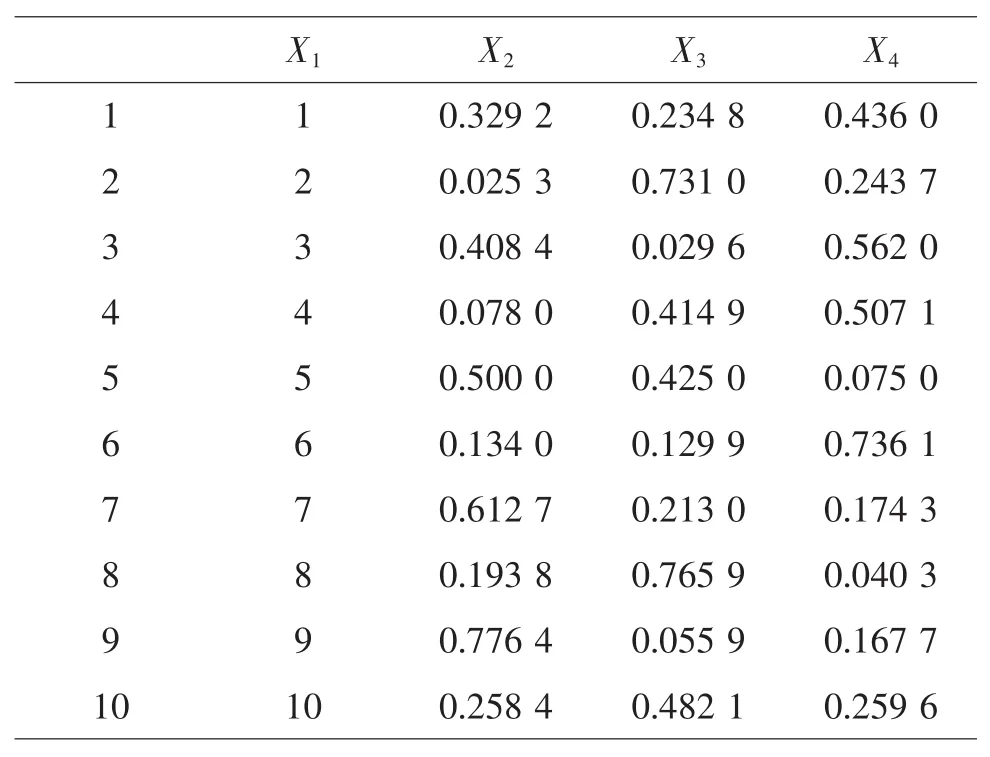
表6 UCM10*(101+3)
2 U10*(108)變換成UCM10*(101+4)
由于配方因素數P=4,查U10*(108)的使用表,選擇1,3,4,5列,過程變量安排在第1列,將混料配方P-1=3 分別安排在 3,4,5 列。對第 3,4,5 列進行變換,得到UCM10*(101+4)表(見表7)。
3 U10*(108)變換成UCM10*(101+5)
由于配方因素數P=5,查U10*(108)的使用表,選擇 1,3,4,5,7 列,過程變量安排在第 1 列,將混料配方 P-1=4 分別安排在 3,4,5,7 列。對第 3,4,5,7 列進行變換,得到UCM10*(101+5)表(見表8)。
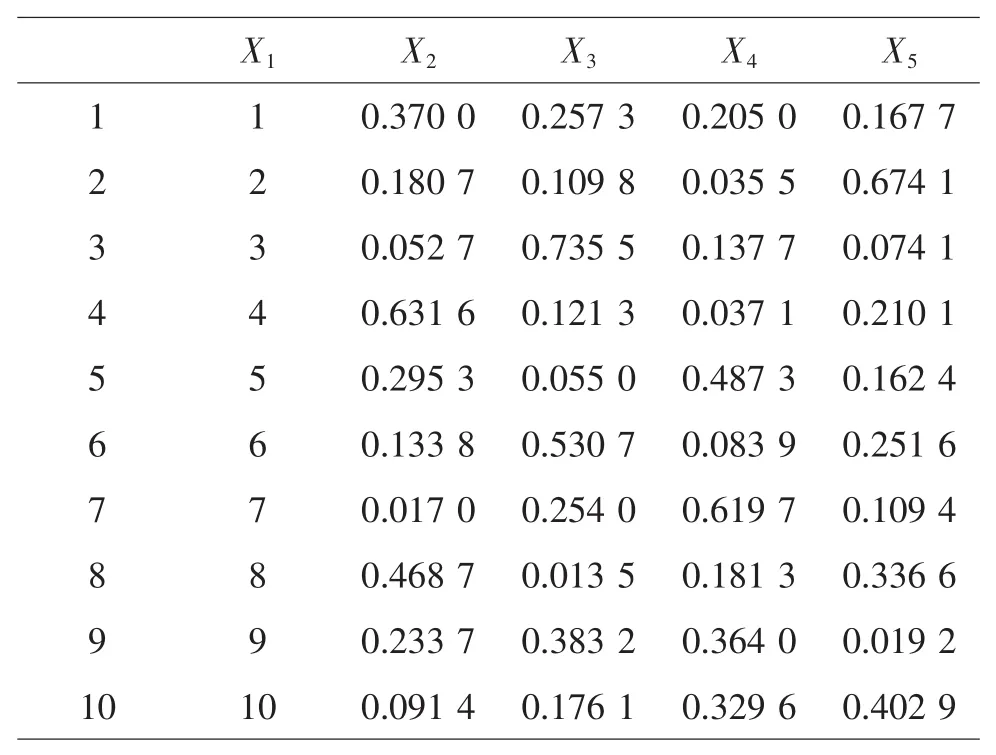
表7 UCM10*(101+4)
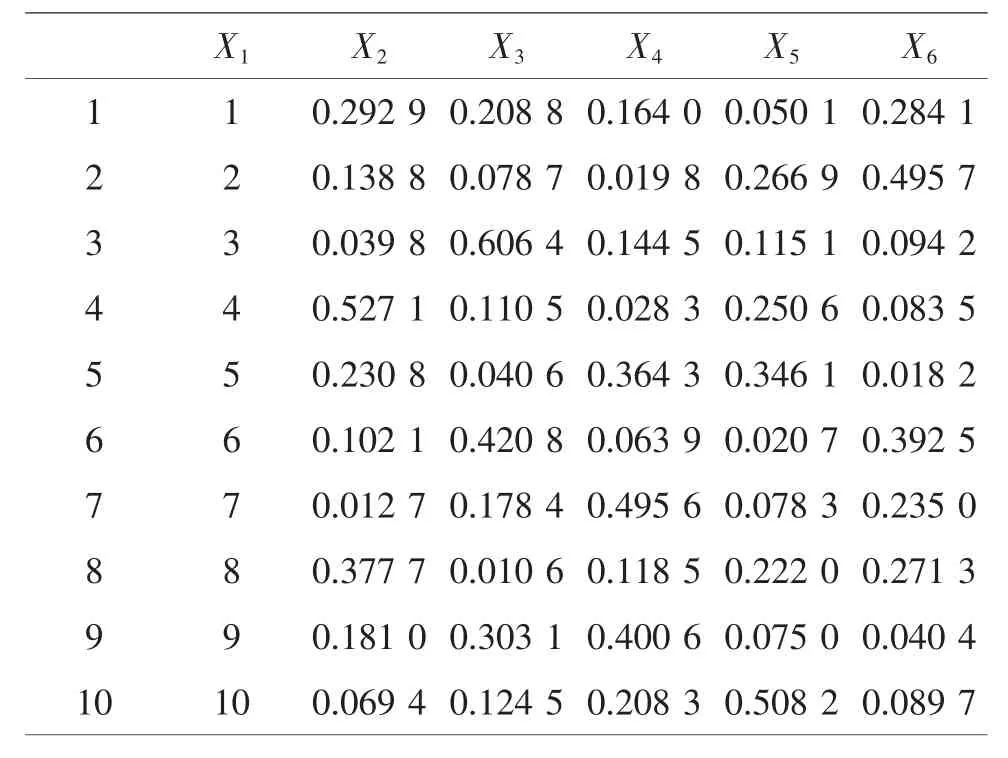
表8 UCM10*(101+5)
4 U10*(108)變換成UCM10*(102+3)
雖然配方因素數P=3,但由于過程變量為2,使用表因素應為C+P-1=4,查U10*(108)的使用表,選擇1,3,4,5 列,過程變量安排在第 1,3 列,將混料配方P-1=2分別安排在4,5列。對第4,5列進行變換,得到UCM10*(102+3)表(見表9)。
5 U10*(108)變換成UCM10*(102+4)
使用表因素應為C+P-1=5,查U10*(108)的使用表,選擇 1,3,4,5,7 列,過程變量安排在第 1,3 列,將混料配方P-1=3分別安排在4,5,7列。對第4,5,7列進行變換,得到UCM10*(102+4)表(見表10)。
6 U10*(108)變換成UCM10*(102+5)
使用表因素應為C+P-1=6,查U10*(108)的使用表,選擇 1,2,3,5,6,8 列,過程變量安排在第 1,2列,將混料配方P-1=3分別安排在3,5,6,8列。對第3,5,6,8列進行變換,得到UCM10*(102+5)表(見表11)。
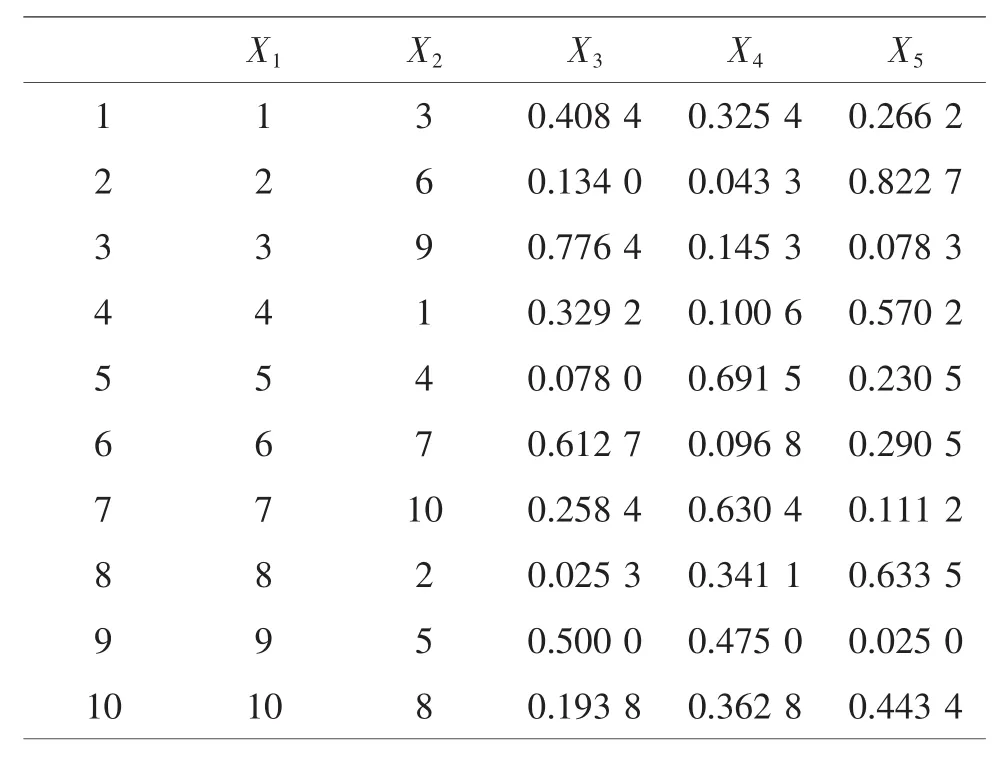
表9 UCM10*(102+3)
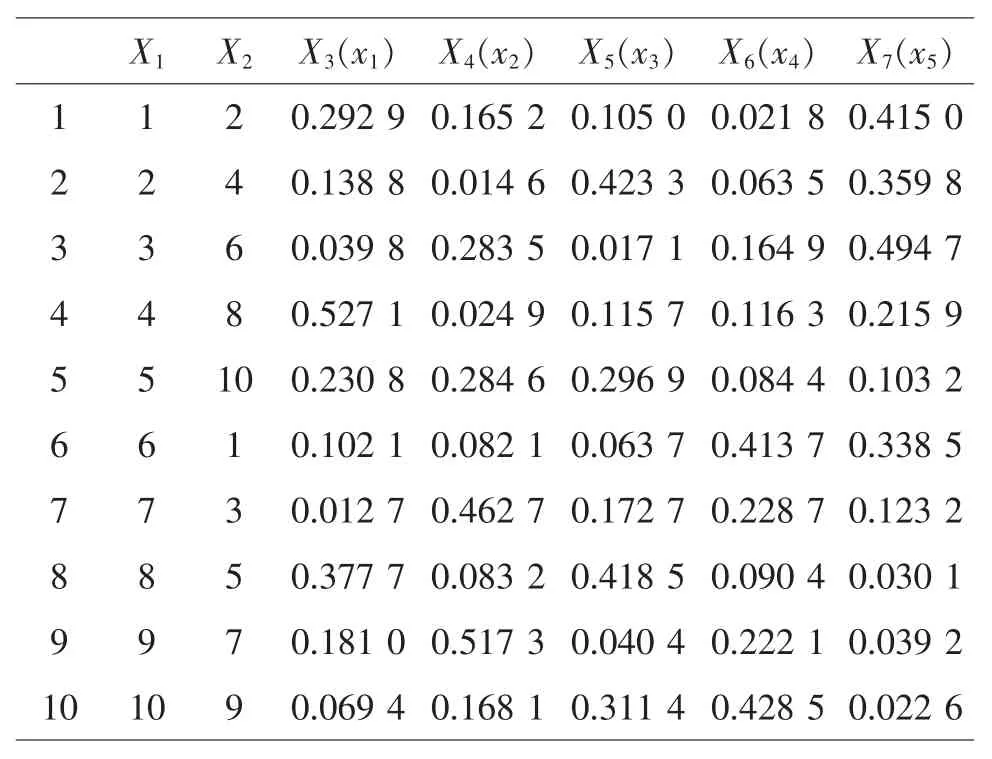
表11 UCM10*(102+5)
7 U10*(108)變換成UCM10*(103+3)
使用表因素應為C+P-1=5,查U10*(108)的使用表,選擇 1,3,4,5,7 列,過程變量安排在第 1,3,4列,將混料配方P-1=2分別安排在5,7列。對第5,7列進行變換,得到UCM10*(103+3)表(見表12)。
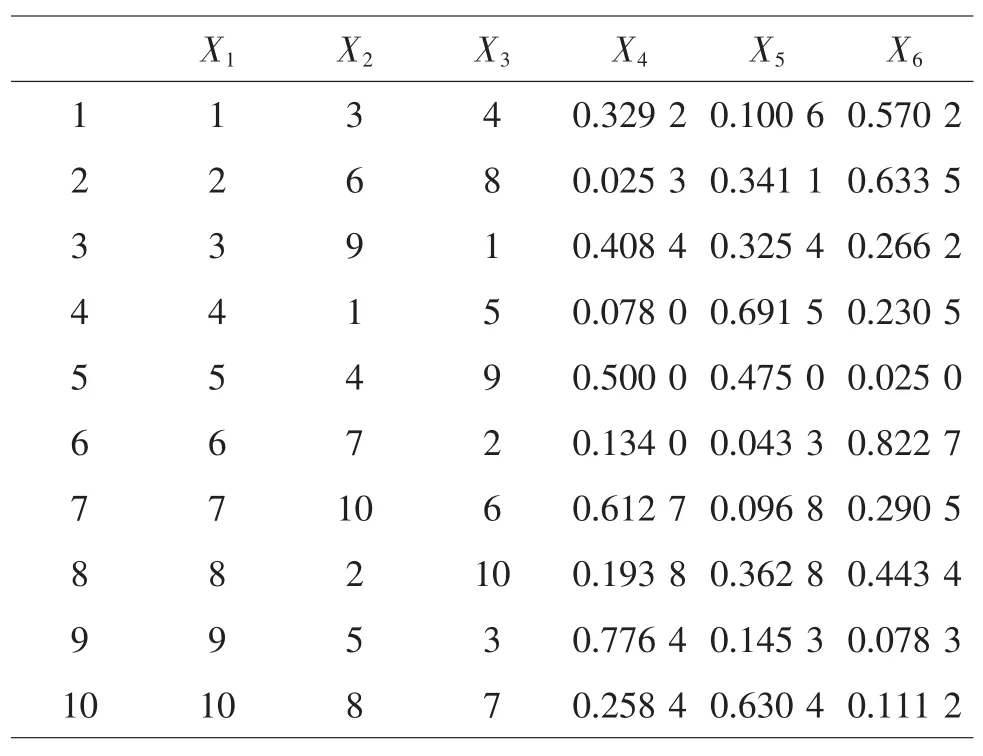
表12 UCM10*(103+3)
8 U10*(108)變換成UCM10*(103+4)
使用表因素應為C+P-1=6,查U10*(108)的使用表,選擇 1,2,3,5,6,8 列,過程變量安排在第 1,2,3列,將混料配方P-1=3分別安排在5,6,8列。對第5,6,8列進行變換,得到UCM10*(103+4)表(見表13)。
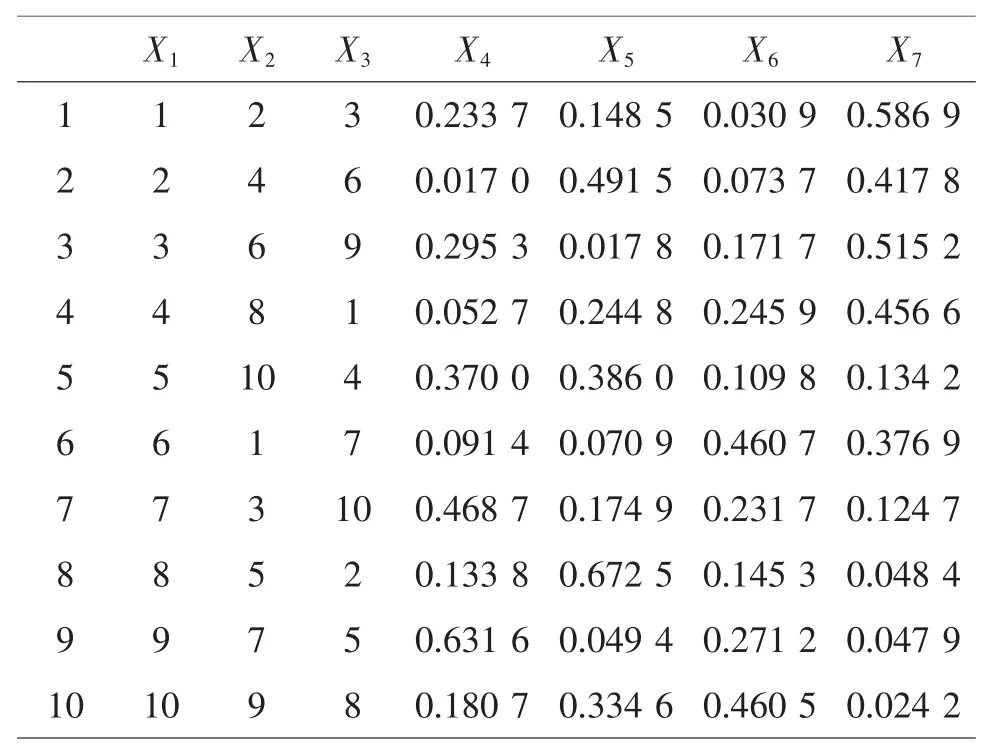
表13 UCM10*(103+4)
需要特別強調的是本文和本刊2018年第二期刊登的第二十二講“混料均勻設計簡介”是上下篇,對于混料配方部分適用于無約束、下限約束以及有上下限約束但可調整為正單形的混料試驗。對于不能調整為正單形的有上下限約束的混料試驗,我們還將進一步介紹和討論。
本文定稿于2015年元旦,窗外陽光明媚。

