基于廣義互相關的時延估計算法研究*

朱 超，屈曉旭，婁景藝

（海軍工程大學 電子工程學院，湖北 武漢 430033）

0 引 言

時延作為用來表征信號特征的一個重要參數，隨著信號處理技術的廣泛應用，如何快速準確地獲得信號的時延，成為信號分析與處理領域人們研究的熱點問題。時延估計要解決的主要問題是對接收目標信號進行處理，準確快速地估計和測量接收信號之間因信號傳播過程中通道的不同而引起的時間延遲[1]。目前，應用于時延估計的技術有廣義互相關法、二次相關法、LMS自適應濾波器法、高階累積量法和廣義雙譜法等[2]，盡管以上算法原理有所不同，但是它們之間總存在信號相關性的成分。所以，研究廣義互相關時延估計算法對需要處理時延的有關領域具有重要意義。由于廣義相關時延估計算法簡單、計算量小，其應用比較廣泛。本文對廣義互相關時延估計算法原理進行研究，并利用廣義互相關時延估計算法的不同加權函數進行仿真比較，分析了其各自的優點與不足。

1 基本互相關的時延估計算法

互相關（CC）是用來比較兩個信號或函數在時域相似程度的基本方法。時延估計的基本思想是利用兩個接收信號的互相關函數來估計時間延遲[3]。時延估計算法可以通過以下兩個信號模型來分析：信源發射信號s(t)經兩個傳輸通道傳輸的過程中加入了伴有噪聲的信號x1(t)和x2(t)。設信號x1(t)和x2(t)滿足：

其中，A1和A2是發射信號的幅度參量，表示s(t)經不同通道傳輸后的幅度增益和相位偏移。n1(t)和n2(t)代表未知的加性平穩高斯白噪聲，τ1和τ2表示信號傳輸的時延，且τ1≤τ2。為表達方便，以x1(t)為標準進行歸一化，則式（1）可以重新表示為：

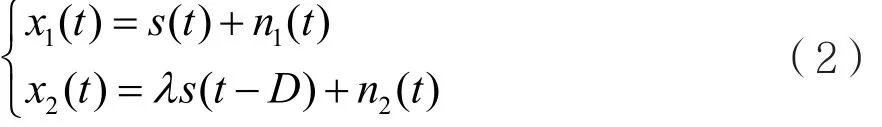
式（2）離散形式為：

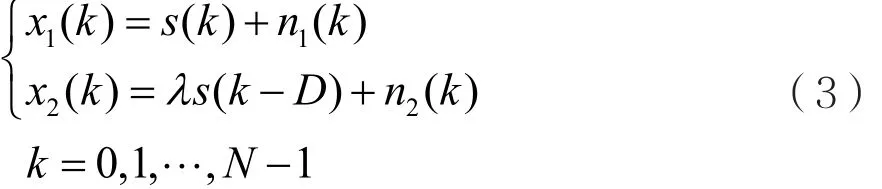
其中λ=A2/A1，表示兩個接收信號的幅值比；D=τ2-τ1，表示所求時延值。

x1(t)和x2(t)的互相關函數表示為：

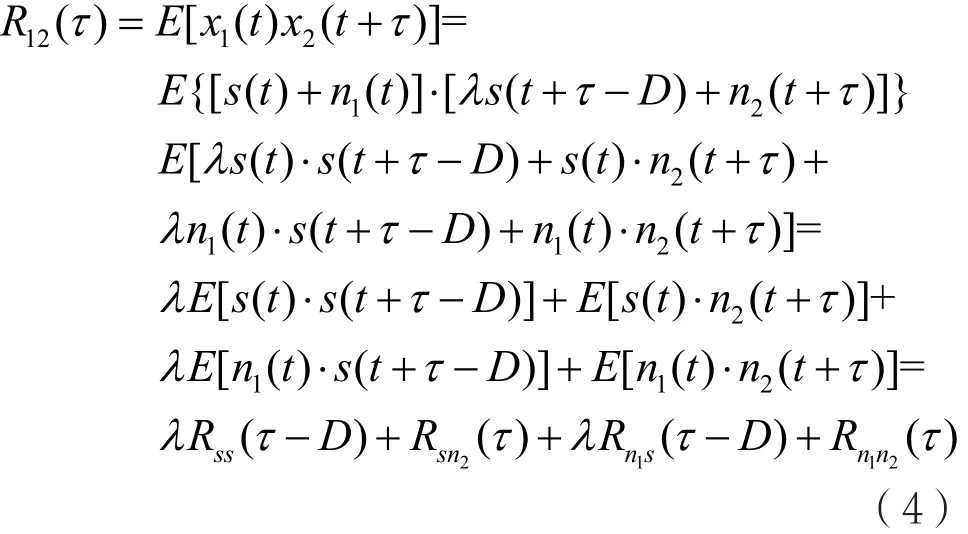
假設n1(t)和n2(t)是獨立于s(t)平穩不相關的高斯白噪聲，則兩個噪聲n1(t)、n2(t)與信號s(t)的互相關函數為：

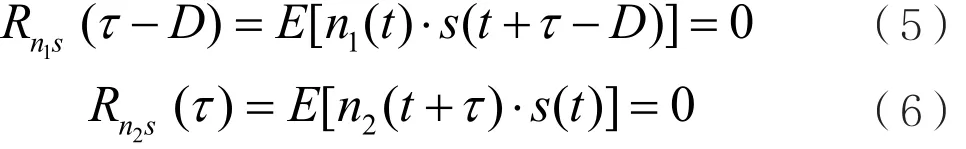
噪聲n1(t)與n2(t)的互相關函數為：

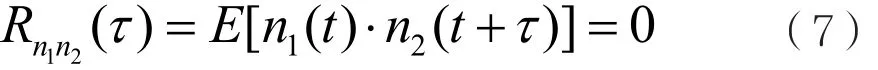
則：

由自相關函數|RSS(τ)|≤Rss(0)的性質可知，當τ=D時，Rss(τ-D)最大，即R12(τ)也達到最大。因此，求得R12(τ)峰值對應的τ，就是兩個接收信號之間的時延。

在以上推導過程中，假設信源發射信號與噪聲信號之間、噪聲信號與噪聲信號之間都是不相關的，式（4）中的信號也被默認是無限長的序列。但是，在實際時延估計過程中，由于采集到的接收信號序列長度不可能無限長，時延估計時只能用有限長序列的信號代替推導中的無限長序列信號。此外，受到實際操作中信號噪聲的相關性和其他不良因素的影響，式（4）中的計算結果并不準確，相關函數的最大值可能會被弱化，甚至會出現多個峰值，由此帶來的誤差會影響時延估計的穩定性。

2 廣義互相關時延估計算法

為了克服基本互相關的時延估計中的缺陷，提出了廣義互相關（Generalized Cross Correlation，GCC）時延估計算法。它利用加權函數增強信號中信噪比的作用，從而提高了時延估計精度[4]。利用兩個接收信號x1(t)和x2(t)進行基于加權函數的廣義互相關來估計時間延遲，是此算法的基本思想。在此基礎之上，通過頻域加權函數對信號進行前置濾波，盡量抑制噪聲的干擾，然后對加權后的函數進行互相關運算可獲得其峰值，工作原理如圖1所示。

圖1 廣義互相關時延估計工作原理

根據維納—辛欽定理可知，互相關函數與其互功率譜密度互為傅里葉變換對，則x1(t)和x2(t)的互相關函數又可以表示為：

其中，G12(ω)是x1(t)和x2(t)的互功率譜函數。當x1(t)和x2(t)經過濾波后，輸出信號的互功率譜函數可以寫為：

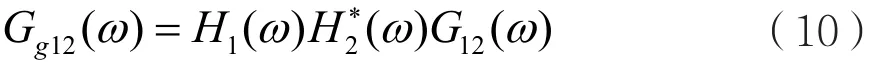
其中，H1和H2表示濾波函數，(ω)表示H2(ω)取共軛。所以，信號x1(t)和x2(t)的廣義互相關函數可表示為：

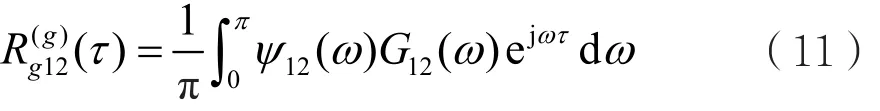
其中，ψ12(ω)=H1(ω)H2*(ω)，表示廣義頻域加權分量。在時延估計過程中，可以通過選取不同加權函數來針對不同類型的干擾噪聲進行適當的濾波處理，從而有效抑制噪聲干擾的影響[5]，然后會使得R12(τ)有一個峰值相對較大、較尖銳，其對應的橫坐標即為所求時延，從而提高時延估計精度。

廣義互相關時延估計算法流程，如圖2所示，圖中( )*表示取共軛運算。

圖2 廣義互相關時延估計算法流程

在廣義互相關時延估計算法流程中，先對兩個通道的接收信號分別進行快速傅里葉變換FFT（Fast Fourier Transform），然后計算它們的互功率譜，在頻域對接收信號的互功率譜G12(ω)進行加權函數計算，將結果進行快速傅里葉逆變換IFFT（Inverse Fast Fourier Transform），最后得到的互相關函數的峰值就對應了兩個通道的接收信號的時延差τ。為了比較不同加權函數對接收信號進行濾波的效果，本文采用了加權函數，如表1所示。

表1 加權函數表達式及其特性

3 仿真與分析

為了分析研究不同加權函數在不同信噪比環境下廣義互相關時延估計算法對時延估計性能的影響，下面通過MATLAB構造加有平穩高斯白噪聲的兩個通道接收信號進行仿真實驗。仿真中采用的信號是幅度為5、頻率為10 kHz、長度為1 024的正弦波信號，采用500 kHz的采樣頻率對兩個通道接收到的信號進行采樣。假設兩個信號之間延遲為10個采樣間隔，即延遲時間τ=0.02 ms的正弦波來仿真模擬兩個不同通道的接收信號，其中噪聲是平穩高斯白噪聲。假設信號與噪聲、噪聲與噪聲都是相互獨立的，在信噪比為10 dB的環境下，兩個仿真接收信號的波形如圖3所示，基本互相關時延估計算法的仿真結果如圖4所示。采用PHAT加權函數算法、Roth加權函數算法、SCOT加權函數算法和HB加權函數算法的廣義互相關時延估計算法，仿真結果分別如圖5（a）、圖5（b）、圖5（c）和圖5（d）所示。

通過對比圖4和圖5可以看出，利用廣義互相關得到的時延估計消弱了接收信號中周期性干擾信號的影響，且其互相關函數峰值也更尖銳。其中，Roth加權函數算法表現出的抗干擾噪聲能力較弱，且時延估計仿真中出現了次峰波動較大的現象，進而其互相關函數的主峰值則幾乎淹沒在噪聲干擾中。HB加權函數算法相比PHAT加權函數算法、SCOT加權函數算法和Roth加權函數算法的互相關函數的峰值，更加尖銳。HB加權函數算法的相關函數主峰值受次峰值影響較小，抗噪聲干擾能力得到了提高，所以能夠表現出較好的穩定性，但也存在次峰波動現象。

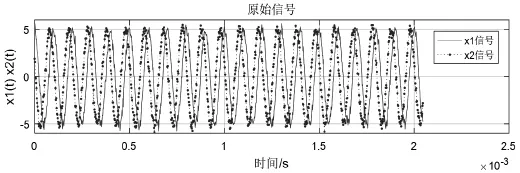
圖3 兩個仿真接收信號波形

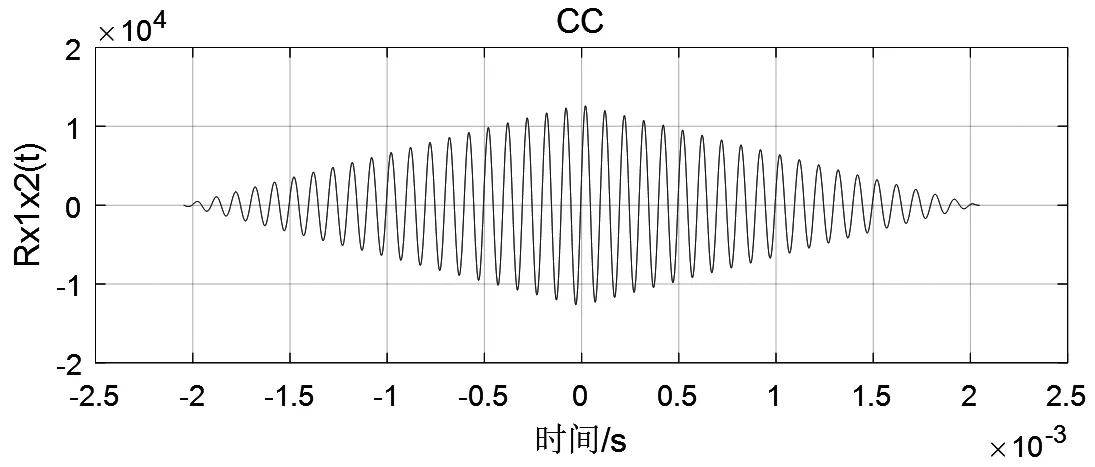
圖4 基本互相關算法仿真結果

圖5 信噪比10 dB時不同加權算法比較

在信噪比為20 dB的環境噪聲下，不同加權函數算法時延估計算法仿真結果如圖6所示。

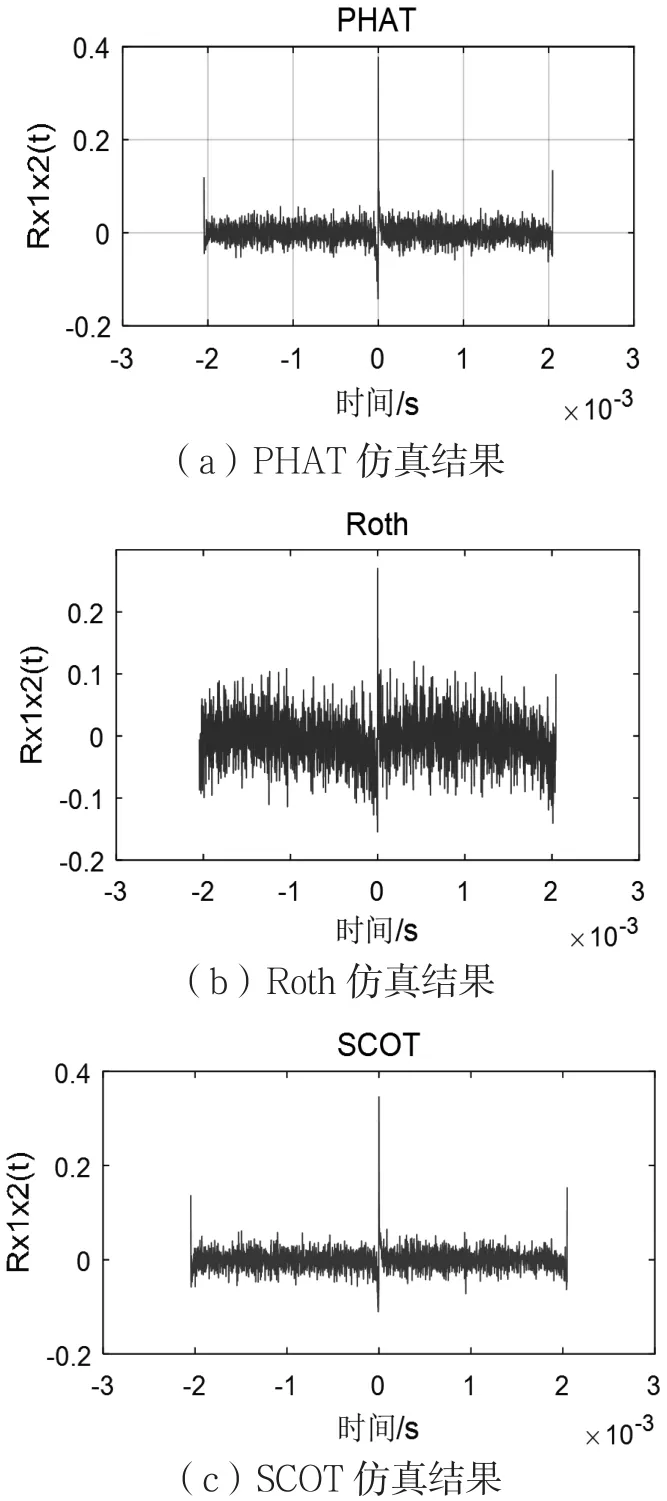
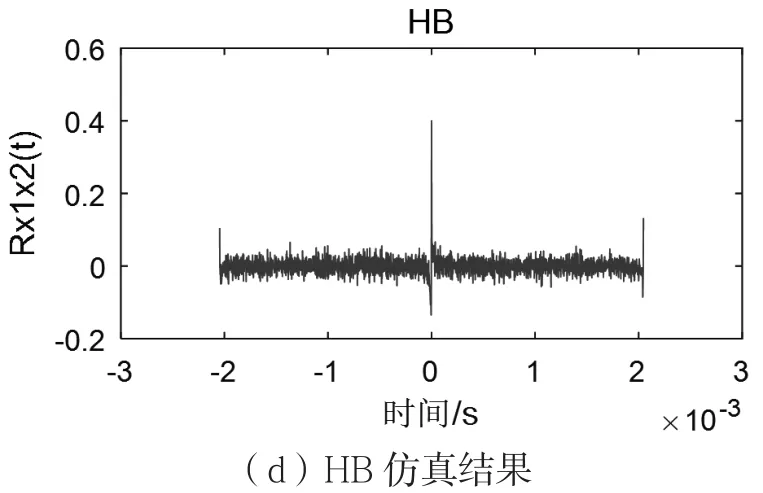
圖6 信噪比20 dB時不同加權算法比較

通過比較圖5和圖6可知，隨著信噪比的增高，幾種加權函數算法時延估計的仿真效果對比較為鮮明。信噪比較高時，4種加權函數算法時延估計的互相關函數峰值均被明顯凸現出來，而Roth的峰值受噪聲影響較大，即抗噪聲性能也比另外3種略弱。隨著信噪比的降低可以看出，經Roth加權函數算法處理后的峰值幾乎被淹沒在噪聲中，另外3種加權函數算法對接收信號的互相關處理后，峰值也會有所減弱，但還具有一定的抑制噪聲能力。

在信號長度為1 024、采樣頻率為500 kHz的MATLAB仿真中發現，時延估計的精確性達不到期望的理想狀態。為了分析接收信號的長度對廣義互相關時延估計在不同加權函數算法的性能影響，本文在信噪比為40 dB的環境噪聲下，采用兩個不同通道的接收信號幅度為5、頻率為10 kHz、信號長度為1 024 000的正弦信號，采用的采樣頻率同樣是500 kHz，兩個信號之間的延遲為10個采樣間隔時的時延估計仿真，仿真結果如圖7所示。

圖7 信號長度1 024 000時不同加權算法比較

在不同長度的接收信號仿真中，信號長度越長，不同加權函數算法的廣義互相關時延估計總體效果越穩定，其中PHAT加權函數算法、SCOT加權函數算法和HB加權函數算法的時延估計最接近，都比Roth加權函數算法有更高的抗噪聲性能。仿真也發現，隨著信號長度的減小，廣義互相關時延估計精度性能達不到估計效果，從而導致時延估計失效。

信號長度為1 024 000、估計延時為0.02 ms時，不同加權函數算法仿真運行結果如表2所示。

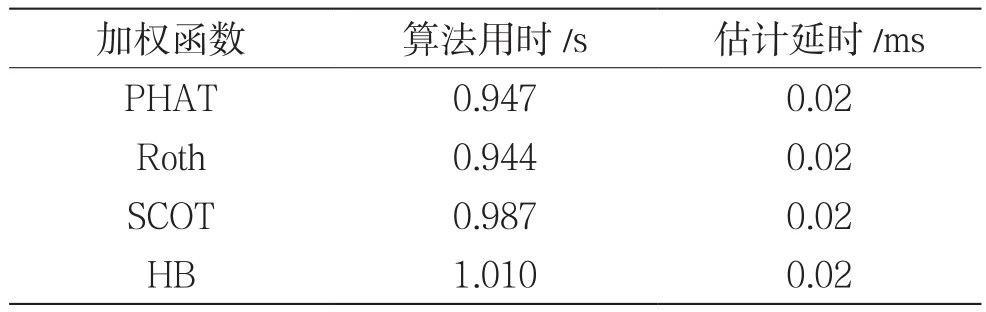
表2 不同加權函數算法仿真運行結果

從表2的運行結果可以看出，不同加權函數算法估計時延的時間是不同的。通過仿真得知，信號長度越長，算法運行時間越久，相同信號長度的時延估計中，Roth加權函數算法運行時間最短，HB加權函數算法運行時間最長。

綜合以上分析結果可以得出，HB加權函數算法的互相關函數值的峰值更為尖銳，相對次峰更少，所以受次峰值影響較小。信噪比越大，接收信號的長度越長，算法用時越多，同時時延估計的準確性越高。相同接收信號長度，不同加權函數算法的時延估計時間也略有差別。使用HB加權函數算法得到的時延估計性，在以上4種加權函數算法中，抗噪性能和時延估計精度表現最好，即表現出較好的穩定性。

4 結 語

廣義互相關時延估計算法是信號處理中時延估計領域的經典算法，具有較高的估計精度。但是，在低信噪比情況下，次峰值波動明顯且使得相關函數的峰值受到壓制，估計性能會惡化。本文經MATLAB仿真研究得出：信噪比越大，接收信號長度越長，時延估計效果越理想；Roth加權函數算法具有一定的抗噪聲能力，但其性能相比于SCOT加權函數算法、HB加權函數算法及PHAT加權函數算法，表現略有不足，HB加權函數算法表現出較好的穩定性。本文只是進行了廣義互相關時延估計算法的理論研究，實際中應該根據具體實際環境選取不同的算法。時延估計技術在雷達、衛星、聲吶等領域均有重要的應用，所以如何在低信噪比環境下改進廣義互相關時延估計算法，是今后需要研究的重點和方向。

參考文獻：

[1] Knapp C H,Carter G C.The Generalized Correlation Method for Estimation of Time Delay[J].IEE Trans on ASSP,1976,24(04)：320-327.

[2] 孫洋,徐慨,楊海亮.基于廣義互相關時延估計算法的性能分析[J].計算機與數字工程,2013,41(01)：33-34,144.SUN Yang,XU Kai,YANG Hai-liang.Analysis of Performance Based on Generalized Cross-correlation Delay Estimation[J].Computer Engineering and Digital Engineering,2013,41(01)：33-34,144.

[3] 茅惠達,張玲華.聲源定位中廣義互相關時延估計算法的研究[J].計算機工程與應用,2016,52(22)：138-142.MAO Hui-da,ZHANG Ling-hua.Generalized Crosscorrelation Time Delay Estimation Algorithm for Sound Source Localization[J].Computer Engineering and Applic ations,2016,52(22)：138-142.

[4] 景思源,馮西安,張亞輝.廣義互相關時延估計聲定位算法研究[J].聲學技術,2014,33(05)：464-468.JING Si-yuan,FENG Xi-an,ZHANG Ya-hui.Study of Generalized Correlation Delay Estimation Acoustic Localization Algorithm[J].Acoustics Technology,2014,33(05)：464-468.

[5] 胡小鋒,劉衛東,王雷等.廣義互相關電暈放電輻射信號時延估計方法[J].強激光與粒子束,2018(01)：56-60.HU Xiao-feng,LIU Wei-dong,WANG Lei,et al.A Method for Time Delay Estimation of Corona Discharge Radiation Signal based on Generalized Cross-correlation[J].High Power Laser and Particle Beams,2018(01)：56-60.

[6] 金中薇,姜明順,隋青美等.基于廣義互相關時延估計算法的聲發射定位技術[J].傳感技術學報 ,2013,26(11)：1513-1518.JIN Zhong-wei,JIANG Ming-shun,SUI Qingmei,et al.Acoustic Emission Location based on Generalized Cross-correlation Time Delay Estimation Algorithm[J].Chinese Journal of Sensors and Actuari es,2013,26(11)：1513-1518.