Fault Estimation and Accommodation for a Class of Nonlinear System Based on Neural Network Observer

， ，

College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，P．R．China

0 Introduction

As engineering systems and industrial processes become more and more complex，the requirements for system reliability and security are continuously growing．Once the system fails，it may lead to performance degradation，sometimes even system break－down．So，this necessity has motivated a significant research in the modelbased fault tolerant control （FTC）techniques which need early fault detection （FD）and isolation （FI）［1－4］．

The most common approaches for modelbased FD are based on the state or parameter estimation schemes，which employ techniques such as the adaptive observer［5］，the sliding mode observer［6］and the geometric approaches［7］．Among these studies，adaptive observer－based approaches have been extensively considered due to their extensive applicability and good fault reconstruction capability［5，8－14］．An adaptive observer has been employed to diagnose the actuator and sensor faults in the linear time－varying systems in Ref．［8］．This scheme needs certain necessary conditions which limits its application．Zhang et al．presented a fault diagnosis and isolation scheme for a class of Lipschitz，uncertain nonlinear systems with partial state measurements［13］，while the fault functions are assumed to be linear in parameters with known functions．Recently，neural networks（NNS）has been applied to the fault diagnosis problem because of its good capabilities in function approximation［15－16］．An adaptive fault diagnosis scheme was developed［15］where neural network was employed to approximate the nonlinearities．Multiplicative actuator fault detection scheme using online neural network learning are designed and analyzed，but the faults are not estimated［16］．

Fault accommodation is the strategy to achieve desired performance where the controller reacts to the occurrence of faults［17－22］．A fault tolerant controller was proposed based on adaptive observer［18］，but the solution between the fault estimation observer and fault tolerant control was in a certain coupling．In Ref．［21］，a new method of fault accommodation scheme was proposed with the neural network to approximate the nonlinear system，while the system state was known before hand．

The motivation of our work is to establish a novel adaptive fault estimation and accommodation scheme for Lipschitz nonlinear systems subject to actuator or component faults．To estimate the fault，an observer based on adaptive control and neural network techniques is designed．Then，a fault tolerant controller is developed to compensate for the fault effects for the systems．

1 Problem Statement

Consider a fault－free nonlinear system

wherex（t）∈Rnrepresents the unknown state vector，y（t）∈Rpthe measurable output vector，andu（t）∈Rmthe control input vector．（x，u，t）andd（t）∈Rqare the smooth vector fields that represent the known dynamics of the nominal model and an external disturbance vector which satisfies‖d（t）‖≤μ1，respectively，andA，B，C，Dthe known matrices with proper dimensions．

Suppose there occurs faults which are usually mixed with system states and inputs，then the system can be expressed as

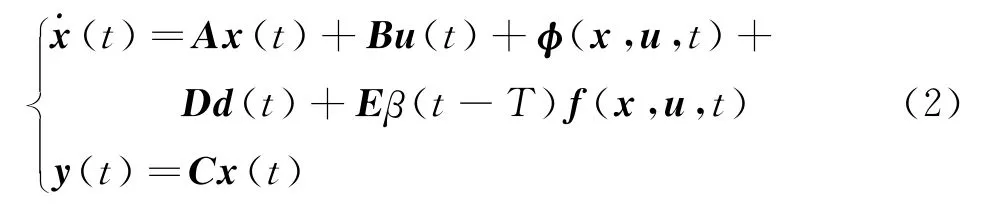
wheref（x，u，t）∈Rrdenotes unknown time－varying fault function which can not only represent actuator faults but also system component faults，andEthe fault distribution matrix with proper dimension．β（t－T）describes the time profile of the fault with the following form

whereT≥0is the unknown fault occurrence time．

Assumption 1 （A，C）is observable and（A，B）is controllable．

Assumption 2 The nonlinear term（x，u，t）is Lipschitz inxwith Lipschitz constantγ，i．e．

‖（x，u，t）－（，u，t）‖ ≤γ‖x－‖（4）

Lemma 1 Assume thatXandYare vectors or matrices with appropriate dimensions，then for any positive scalarα，the following inequality holds

In this paper，the radial basis function neural network （RBFNN）is used to approximate the unknown fault functionf（x，u，t）．The RBFNN is a kind of single－hidden－layer neural network which is composed of three layers：The input layer，hidden layer and output layer．

whereW＊＝ ［，，…，］Tis the ideal weight matrix，X＝［xTuT］T∈Adthe input vector including the state vector and input vector．σ＝［σ1，σ2，…，σN］Tis the radial basis function and is usually chosen asσi＝exp（－‖X－δi‖2／）with centre vectorδiand widthdi，andNthe node number of hidden layer．Suppose

whereWis the real weight vector andwm＞0the designed parameter．

Assumption 3εis the optimal approximation error and is bounded，that is｜ε｜≤ε0，ε0can be taken arbitrarily small．

2 Adaptive Fault Diagnosis Observer

Based on system （2），the following fault diagnosis observer is constructed

where（t）（t），u，t）are the estimations ofx（t），y（t），f（x，u，t），respectively，Lis the observer gain matrix．Then the adaptive fault estimation algorithm is given by

whereandare the estimations of ideal weight vector and centre vector，respectively．In the practical applications，the value of weight and center of RBFNN have great impact on the approximation error while the influence of the width vectordis small，sodis designed to be constant．Denote：ex＝x－，ey＝Cex，ef＝f－f．Then the error dynamic equation can be presented as

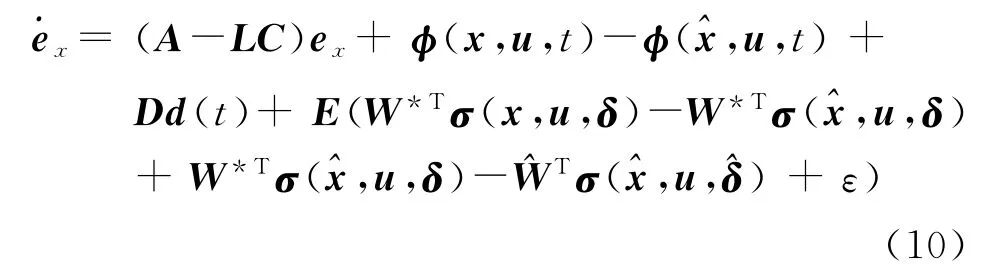
In order to analyze，the Taylor′s series ofσ，u，δ）is expanded atδ，that is

whereis high－order items and is bounded．Then one has

Substituting Eq．（12）into Eq．（10），the error dynamic is described by

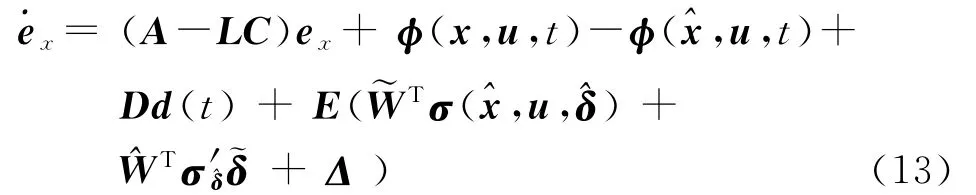
whereandwith‖Δ‖≤μ2．

To guarantee the observer′s stability，the following theorem is given．

Theorem 1 Under the nonlinear fault system（2）and Assumption 2，if there exists a positivedefinite matrixP，matrixesYandRsatisfying the following conditions where the gain matrix of the observer is given byL＝P－1Y，and the adaptive estimation algorithm are described by

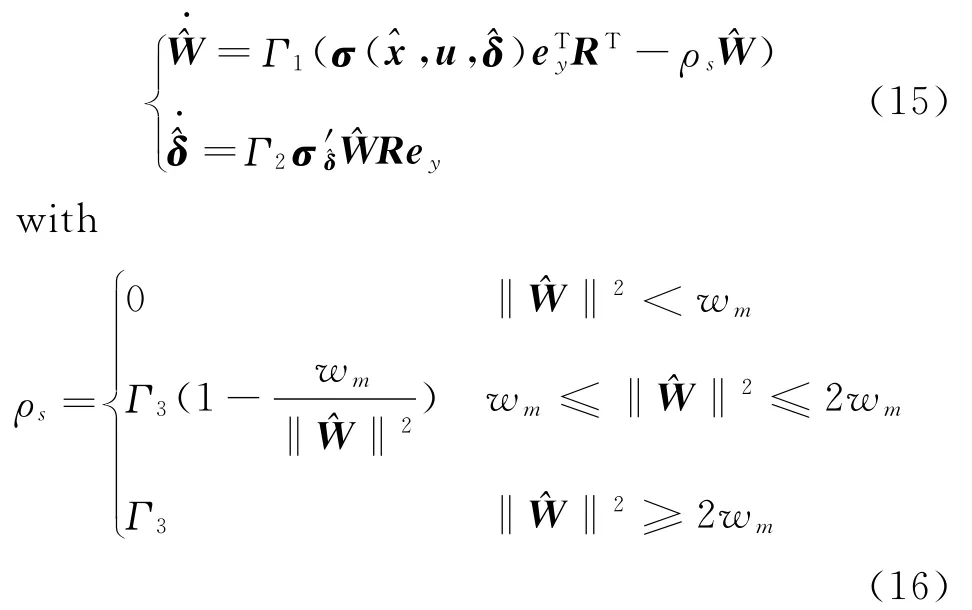
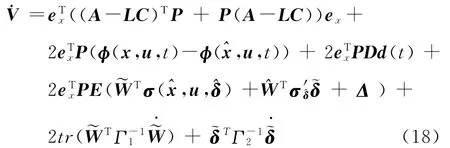
DenoteΔ＝（x，u，t）－，u，t），and according to Lemma 1，the following result is obtained as

五院是華山醫院的對口幫扶單位，作為對口幫扶五院的負責人，華山醫院神經內科副主任醫師韓翔經常往返于兩家醫院，由于距離較遠，每次路上都要耽擱不少時間，于是他想到了借助互聯網，“我們要做的就是，通過互聯網，把本來需要人過去，才能下沉的那些工作，通過互聯網直接下沉下去。”腦卒中智慧醫聯體平臺就是在這樣的初衷之下建立的。韓翔的設想得到了華山醫院領導層的大力支持，最終確認建設目標：探索規劃腦卒中醫聯體平臺，打造研究型、學習型、創新型的基于混合云架構的腦卒中智慧醫聯體平臺。通過閔行地區的示范應用，實現以“區域醫療中心牽頭，三級醫院業務支援，社區醫院鄰里支撐，急救養老康復協同”為特色的智慧腦卒中示范應用。

whereΓ1＞0，Γ2＞0，Γ3＞0，wm＞0are constants which should be designed later and the size ofΓ1will greatly affect the speed of fault estimation．wmis developed to avoid the parameter drift which limits the weight matrixin a convex set，that isΩ＾W＝｛／‖‖2＜wm｝．

Proof

To study the stability and convergence of the proposed observer（8），the following Lyapunov function candidate is considered

whereare both param－eter estimation errors．The time derivative ofVis given by

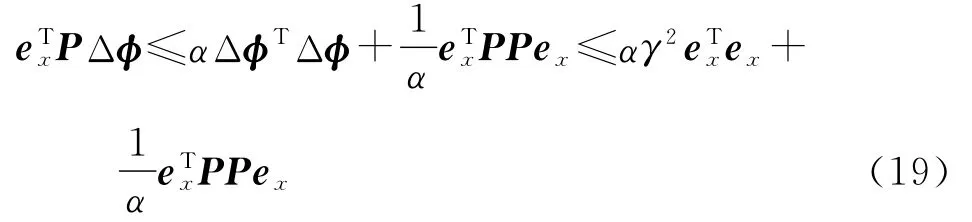
Then one has

If‖‖2＜wm，it can be obtained thatρs＝0

whereandλmaxare the minimum eigen－value and the maximum eigenvalue of matrix，respectively．η＝Dμ1＋Eμ2＞0．

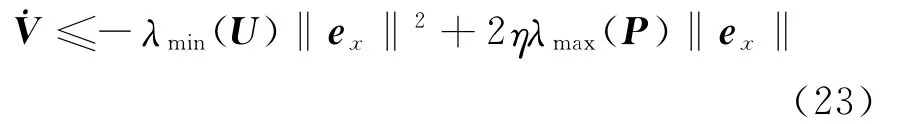
Iftherefore，ex∈L∞∈L∞，∈L∞．These guarantee the stability and convergence of the designed observer by using Barbalat′s Lemma．

3 Fault Tolerant Controller

In many applications，especially those involving safety－critical systems，it is important not only to detect and estimate the characteristic and magnitude of any faults but also to accommodate them as soon as possible．The goal of fault－tolerant control is to maintain dynamic performance in case of failure．In this section，a fault tolerant controller is developed according to Ref．［21］．As the state vectorxis unavailable，the controller is constructed as

whereuH＝α（y）represents a controller that leads the normal system to achieve the desired behavior．uF＝ψ（y，）is an additional control law which should be designed to set stable the following faulty system

Notation［21］R≥0：［0，∞），a functiong：R≥0→R≥0is of classκif it is continuous，strictly increasing，and outputs zero when inputting zero．

And it is of classκ∞if it is unbounded．

Assumption 4 If there exists an normal controlleruH＝α（y），functionsK1（·），K2（·）and Lyapunov functionVHsatisfy the following conditions

whereK1，K2are classκ∞functions．

Theorem 2 In order to ensure that the faulty system（25）is stable，the following control laws are given

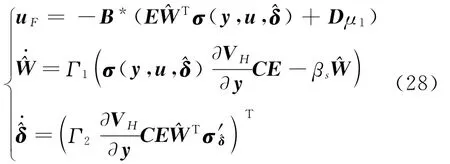
where switchingβs－modification is designed as the same form in Eq．（16），partial differential function ofσ（y）at，andB＊the pseudo inverse ofB．

Proof

To study the stability of the system（25），the following Lyapunov function candidate is considered

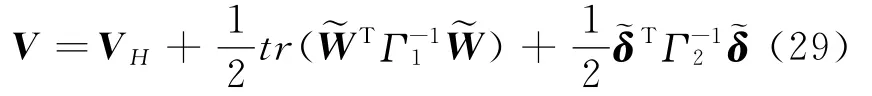
The derivative ofVis

whereW＊TO（y，u）＋εis bound and can approach arbitrary small number such as zero．

Considering control law in Eq．（28），then

where the processing ofρstrT）in Eq．（31）is similar to the previous fault diagnosis observer deignd in Eqs．（21）—（22）．Note thatΔycan be taken arbitrary small such as zero，then we can obtainV≤0，such thaty，，are uniformly bounded．

4 Simulation Results

In this section，the attitude control system for a quadrotor helicopter is considered to verify the efficiency of the proposed algorithm．It is found that actuator of helicopter is very easy to fail，the faults of the four motors will cause the rotor speed to change abruptly or even out of control．The dynamical model of quadrotor attitude systems［23］is

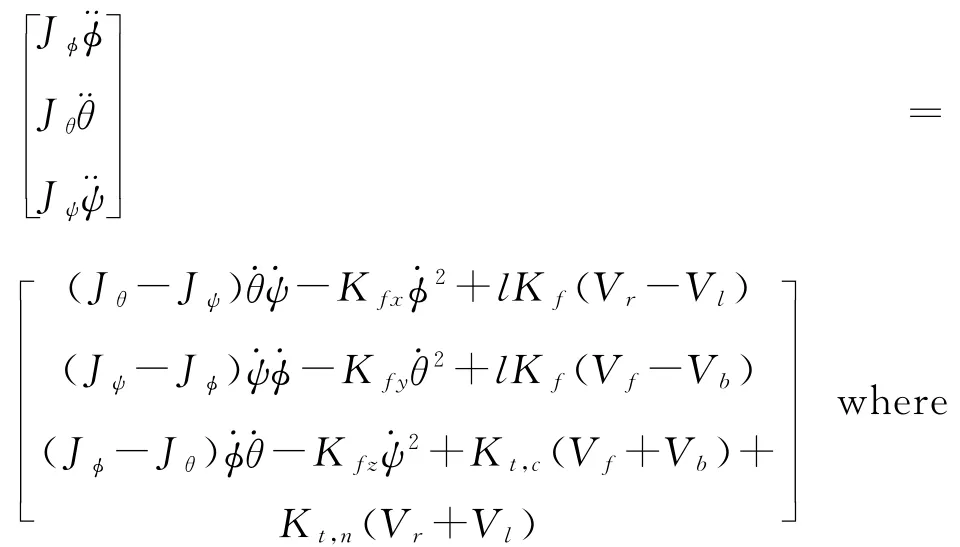
J＝0．005 2，Jθ＝0．005 2，Jψ＝0．11，l＝0．197，Kt，c＝Kt，n＝0．003 6，Kfx＝Kfy＝0．008，Kfz＝0．009 1．，θandψdenote roll angle，pitch angle，yaw angle，respectively；Vf，Vb，Vr，Vlthe voltage of the front，the rear，the right and the left motors，respectively；J，Jθ，Jψthe rotational inertia of roll axis，pitch axis and yaw axis；andKt，c，Kt，nthe counter and the normal rotation propeller torque－thrust constant．Kfrepresents the propeller force－thrust constant andlthe distance between the axis of any rotor and the center of mass．

The aforementioned quadrotor model can be transformed to a common model with faults and disturbances

whereVl］T．The other parameters are given as follows

In this paper，three types of faults are considered．Firstly，assuming voltage failure of the front motor occurs at 10sin the form of low amplitude which fails the helicopter to achieve the desired posture．The fault function is modeled asf（u，t）＝［－0．4 0 0 0］T．

The input of NNS is chosen as the system estimation state，the number of hidden layer nodes is 11andΓ1＝10，Γ3＝0．05I65×1whereI65×1represents a matrix of 65rows and 1column and all elements are 1．wm＝0．2，Γ2＝－0．01．By contrast， the estimation results under the RBFNN fault estimation method and conventional adaptive fault estimation method［19］are shown in Fig．1．

Fig．1 Actuator fault and its estimation

Secondly，assume that the aging of physical structure quadrotor makes voltage of the front motor to be unstable with a continuous jump，and the fault isf（t）＝［0．1sint000］T．By taking learning rateΓ1＝30，wm＝0．02，Γ2＝0．01，Γ3＝0．05I65×1，the estimation results are shown in Figs．2，3．

Fig．2 Actuator fault and its estimation（RBFNN fault estimation method）

Fig．3 Actuator fault and its estimation（conventional adaptive fault estimation method）

Thirdly，assume a physical component fault appears in the quadrotor which leads to parameter changes in the system state matrix．The fault is with the form off（x）＝［x1＋0．05 0 0 0］T．By selecting the learning rateΓ1＝15，Γ2＝0，Γ3＝0．05I65×1，the simulation result is shown in Fig．4．

In view of the above mentioned fault that voltage failure of the front motor occurs at 10s withf（u，t）＝ ［－0．4 0 0 0］T，the node of RBFNN is 11，taking the fault accommodation algorithm in Eq．（28）withΓ1＝0．035，Γ2＝0．07，Γ3＝0．05I65×1．The results are shown in Figs．5—7．It can be seen that the proposed fault tolerant controller can recover the system performance．

Fig．4 Component fault and its estimation

Fig．5 Roll angle with fault accommodation

Fig．7 Yaw angle with fault accommodation

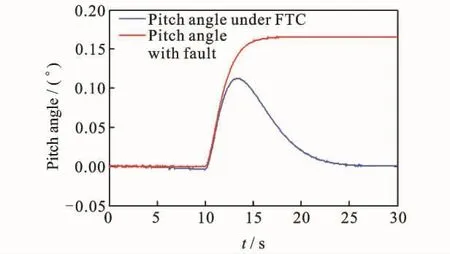
Fig．6 Pitch angle with fault accommodation

5 Conclusions

An adaptive fault estimation and accommodation scheme is proposed for Lipschitz nonlinear systems which are subjected to disturbances and faults．Based on adaptive state observer and RBFNN techniques，a robust adaptive learning algorithm based on switchingβs－modification is developed to estimate the states of the system and actuator or component faults effectively．Meanwhile，not only the weight，but also the centre vector of RBFNN is updated online．Then，a fault tolerant controller is designed to restore system performance．Finally，the simulation results of quadrotor attitude systems validate the efficiency of the proposed techniques．

Acknowledgements

This work was supported by the National Natural Science Foundation of China（No．61533008），the Fund of National Engineering and Research Center for Commercial Aircraft Manufacturing（No．SAMC14－JS－15－053），and the Fundamental Research Funds for the Central Universities（No．NJ20150011）．

［1］ GAO Z，CECATI C，DING S X．A survey of fault diagnosis and fault－tolerant techniques—Part I：Fault diagnosis with model－based and signal－based approaches［J］．IEEE Transactions on Industrial Electronics，2015，62（6）：3757－3767．

［2］ JIANG B，STAROSWIECKI M，COCQUEMPOT V．Fault estimation in nonlinear uncertain systems using robust／sliding－mode observers［J］．IEE Proceedings—Control Theory and Applications，2004，151（1）：29－37．

［3］ JIANG Bin，ZHAO Jing，QI Ruiyun，et al．Survey of fault diagnosis and fault tolerant control of near space vehicle［J］．Journal of Nanjing University of Aeronautics and Astronautics，2012，44（5）：603－610．（in Chinese）

［4］ YIN S，WANG G，KARIMI H R．Data－driven design of robust fault detection system for wind turbines［J］．Mechatronics，2014，24（4）：298－306．

［5］ ZHANG K，JIANG B，SHI P．Fast fault estimation and accommodation for dynamical systems［J］．Control Theory ＆ Applications Iet，2009，3（2）：189－199．

［6］ ALWI H，EDWARDS C．Robust fault reconstruction for linear parameter varying systems using sliding mode observers［J］．International Journal of Robust＆ Nonlinear Control，2015，24（14）：1947－1968．

［7］ de PERSIS C，ISIDORI A．A geometric approach to nonlinear fault detection and isolation［J］．IEEE Transactions on Automatic Control，2001，46（6）：853－865．

［8］ SHAHRIARI－KAHKESHI M，SHEIKHOLESLAM F，ASKARI J．Adaptive fault detection and estimation scheme for a class of uncertain nonlinear systems［J］．Nonlinear Dynamics，2014，79（4）：2623－2637．

［9］ GAO Fei，JIANG Guangwen，ZHANG Zebang，et al．An adaptive observer for actuator and sensor fault diagnosis in linear time－varying systems［C］／／10th World Congress on Intelligent Control and Automation．Beijing：IEEE，2012：3281－3285．

［10］GAO C，DUAN G．Robust adaptive fault estimation for a class of nonlinear systems subject to multiplicative faults［J］．Circuits，Systems，and Signal Processing，2012，31（6）：2035－2046．

［11］MICHAEL D，VELUVOLU K C，RATH J J，et al．Adaptive sensor and actuator fault estimation for a class of uncertain Lipschitz nonlinear systems［J］．International Journal of Adaptive Control ＆Signal Processing，2015，30（2）：271－283．

［12］LI X J，YANG G H．Fault diagnosis for non－linear single output systems based on adaptive high－gain observer［J］．Control Theory ＆ Applications Iet，2013，7（16）：1969－1977．

［13］ZHANG X D，POLYCARPOU M M，PARISINI T．Fault diagnosis of a class of nonlinear uncertain systems with Lipschitz nonlinearities using adaptive estimation［J］．Automatica，2010，46（2）：290－299．

［14］HE S P．Fault estimation for T－S fuzzy Markovian jumping systems based on the adaptive observer［J］．International Journal of Control，Automation and Systems，2014，12（5）：977－985．

［15］LIU C S，ZHANG S J，HU S S．Adaptive neuralnetworks－based fault detection and diagnosis using unmeasured states［J］．Control Theory ＆ Applications Iet，2008，2（12）：1066－1076．

［16］TALEBI H A，KHORASANI K．A neural networkbased multiplicative actuator fault detection and isolation of nonlinear systems［J］．IEEE Transactions on Control Systems Technology，2013，21（21）：842－851．

［17］PATTON R J．Fault－tolerant control：The 1997situation［C］／／Proceedings of IFAC Sym－posium，Fault Detection，Supervision Safety for Process．New York：North－Holland，1997：1033－1055．

［18］JIANG B，STAROSWIECKI M，COCQUEMPOT V．Fault accommodation for nonlinear dynamic systems［J］．IEEE Transactions on Automatic Control，2006，51（9）：1578－1583．

［19］ZHANG K，JIANG B，SHI P．Observer－based fault estimation and accomodation for dynamic systems［J］．Lecture Notes in Control ＆ Information Sciences，2013，436：1－191．

［20］YANG Q，CHEN M．Robust fault－tolerant control for longitudinal dynamics of aircraft with input saturation［J］．Transactions of Nanjing University of Aeronautics and Astronautics，2016，33（3）：319－328．

［21］POLYCARPOU M M．Fault accommodation of a class of multivariable nonlinear dynamical systems using a learning approach［J］．IEEE Transactions on Automatic Control，2001，46（5）：736－742．

［22］HAN J，ZHANG H，WANG Y，et al．Robust fault estimation and accommodation for a class of T－S fuzzy systems with local nonlinear models［J］．Circuits，Systems，and Signal Processing，2016，35（10）：3506－3530．

［23］YANG Huiliao，JIANG Bin，ZHANG Ke．Direct self－repairing control for four－rotor helicopter attitude systems［J］．Control Theory ＆ Applications，2014，31（8）：1053－1060．（in Chinese）