可控磁路式永磁懸浮系統的串級控制
孫 鳳, 周 冉, 夏鵬澎, 金俊杰, 徐方超, 李 強, 金嘉琦
(沈陽工業大學 機械工程學院, 沈陽 110870)
可控磁路式永磁懸浮系統是伺服電機帶動徑向磁化的盤狀永磁鐵,通過改變永磁鐵的旋轉角度來改變磁路,進而調整系統懸浮力的大小,實現系統的懸浮[1]。該系統中懸浮力主要由外部支撐部件導磁體提供的,其與傳統的永磁懸浮系統相比,它是通過改變磁路來控制懸浮力的大小[2],與其他磁懸浮裝置相比,由于該系統的特點,導致在控制方面的難度系數有所增加。
在控制方法方面,PID(Proportional-Integral-Derivative)控制方法[3-5],具有結構簡單、調節參數方便、參數易于整定、適用性強等特點,一定程度上可以使磁懸浮系統的控制精度達到要求,但抗外擾力較弱;魯棒控制方法[6-7],作為一種可以解決系統模型存在不確定參數和抵制系統外部擾動的控制算法,但是結構比較復雜。設計完控制器后,運用Matlab進行仿真[8-10],通過仿真結果來驗證控制器的性能。
隨著高階系統的出現,控制器的設計越來越復雜,然而單環控制方式已經不能滿足對高階系統的控制,為了有效抑制外部擾動和克服該系統自身的強耦合、非線性特性,以及讓控制器設計更簡單,結合傳統PID的設計方法,本文設計了一種串級控制器。此控制器是由角度環和位置環組成的串級控制器,角度環采用PD(Proportional-Derivative)控制,位置環采用PID控制,并對其進行仿真和實驗驗證。該控制器通過系統的兩個測量信號來控制一個執行機構,在一定程度上克服了系統自身特點和外部干擾的影響,使系統的魯棒性得到增強,并且通過這種方式可以使本文的四階系統降為兩個二階系統進行控制,解決了復雜的控制器設計問題,讓控制器的設計更加簡單。通過調整控制器各參數,在跟蹤輸入位移階躍響應的Matlab仿真中表現出了快速跟蹤信號的特點,還有較好的魯棒穩定性。
1 懸浮系統的原理和數學模型
1.1 懸浮原理
如圖1所示,當裝置處于圖1(a)狀態時,盤狀永磁鐵的旋轉角度θ=0°,磁感線不經過懸浮物,而是通過導磁體直接從N極回到S極,所以導磁體對懸浮物不產生磁力;當裝置處于圖1(b)狀態時,永磁體的偏轉角度θ>0°,這時部分從N極出發的磁感線就會通過右邊的導磁體,經過懸浮物,再經過左側導磁體,最終回到S極,這時導磁體就會對懸浮物產生吸引力,另一部分磁感線通過導磁體直接從N極回到S極,在θ從0°到達90°時,吸引力隨著角度的增大而增大。
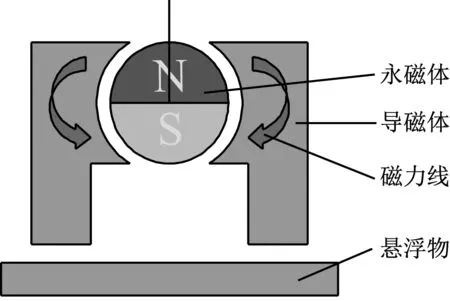
(a) 系統初始狀態
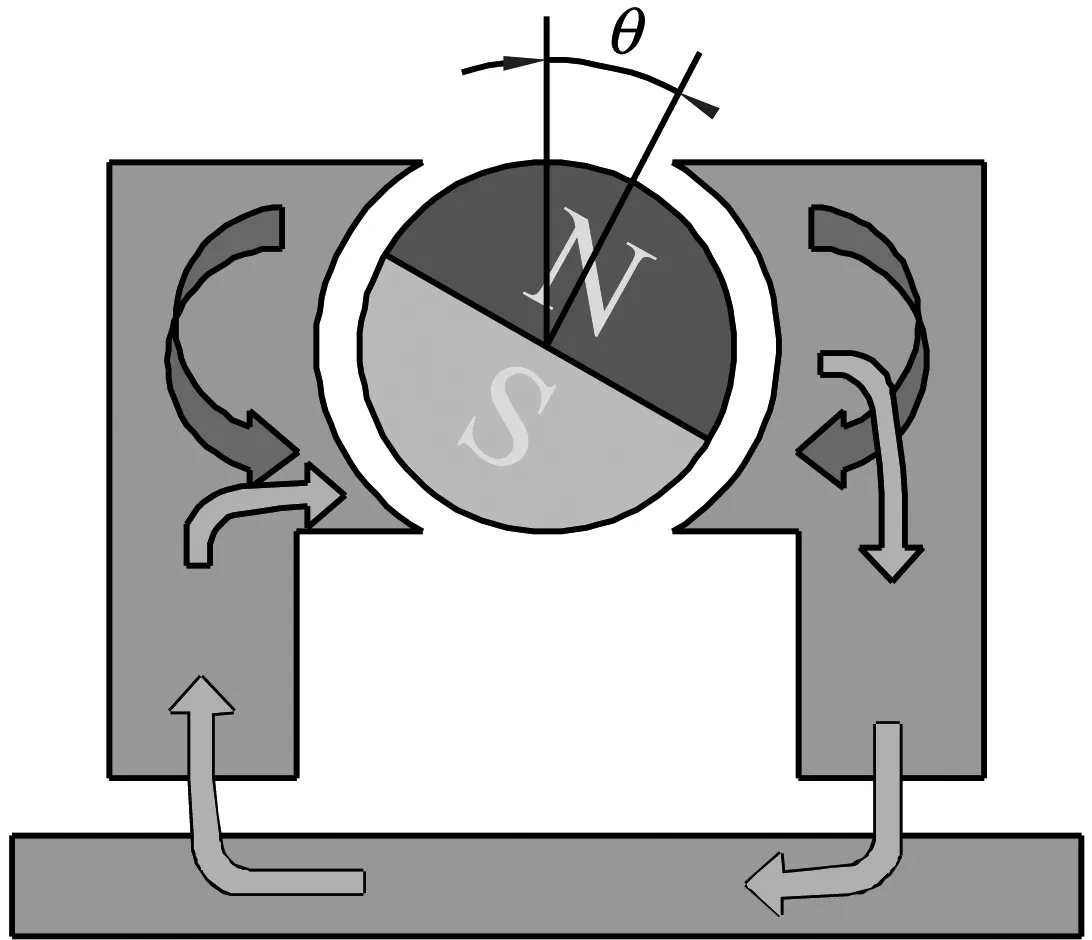
(b) 磁鐵轉角為θ°時
1.2 數學模型
如圖2所示為可控磁路式永磁懸浮系統的模型。圖中fm表示導磁體對懸浮物的磁力;d表示導磁體與懸浮物之間的距離;d0表示在平衡位置時導磁體與懸浮物之間的距離;z表示懸浮物偏離懸浮平衡位置時豎直方向上的變化量;d=d0-z;θ表示盤狀永磁鐵順時針方向的旋轉角度;D表示盤狀永磁體和導磁體之間的距離。
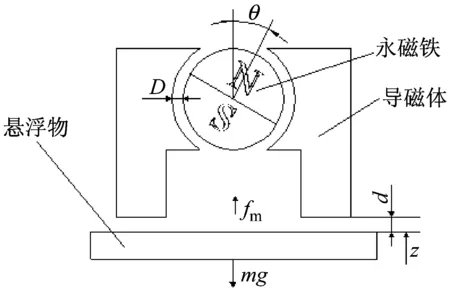
圖2 系統模型圖
懸浮物的懸浮力數學模型
(1)
式中:km為懸浮力系數;Δdf為導磁體和徑向磁化的盤狀永磁體氣隙處的漏磁補償系數。
盤狀永磁體的力學模型
(2)
式中:kτ為徑向磁化的盤狀永磁鐵的轉矩系數;Δdτ為徑向磁化的盤狀永磁體和導磁體氣隙處的漏磁補償系數。
該系統采用伺服電機驅動盤狀永磁體,則系統在平衡位置(d0,θ0)的運動學方程可表達如下
(3)
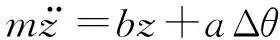
(4)
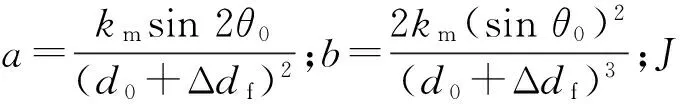
2 串級控制器設計
2.1 控制目標及方案
該永磁懸浮系統懸浮物位置的變化是影響系統穩定的一個重要因素,在控制器設計時要求其能夠快速、穩定的跟蹤參考輸入,保持系統穩定。
按照上述要求,根據串級控制的思想,將系統分為角度環和位置環。角度環的控制目標是使盤狀永磁體的旋轉角度能夠快速的響應參考輸入,即位置環控制器的輸出值;位置環的控制目標是保證系統穩定的跟蹤位置的參考輸入,使懸浮物穩定懸浮。
控制系統結構如圖3所示。由圖可知控制系統以懸浮物的位置Refz為輸入,分別經PID和PD控制環節計算,得到的結果作為輸入實時調節盤狀永磁鐵的回轉角度。

圖3 控制系統結構
為驗證串級控制器對控制系統懸浮穩定的性能,遵循表1所示的系統結構參數進行懸浮特性的仿真和實驗論證。
2.2 角度環控制
本文設計的控制器角度環為內環,位置環為外環,位置控制模式下系統進行兩個環的運算,運算量較大,響應速度較慢,同時如果內環的響應速度慢于環外的響應速度,則無法保證外環的穩定,因此系統角度環的響應速度遠大于位置環。為了簡化計算,可以假設在調節過程中z為零,將由該假設引起的系統模型誤差當做參數擾動引起的模型誤差。內環采用PD控制器,則從參考角度到輸出角度的傳遞函數可表示為
(5)
2.3 位置環控制
角度環采用上述控制后,在特定的變化范圍內近似保證Δθ′(t)=Δθ(t)。外環采用PID控制器,則從參考位移到輸出位移的傳遞函數可表示為
(6)
3 控制特性仿真分析
系統在平衡位置處的各個參數如表1所示。

表1 系統結構參數
選用表1中數據,得控制器參數,kp1=460,kd1=0.8;kp2=400,ki2=2 000,kd2=0.2。利用matlab/Simulink進行抗位移外擾仿真分析,分別對懸浮物的位移z、盤狀永磁鐵的旋轉角度θ、伺服電機電流i進行跟蹤,得到結果如圖4所示。
在系統處于平衡狀態的情況下,在0.2 s時,給系統輸入一個0.1 mm階躍位移信號,經過串級控制,使懸浮物最后達到穩定懸浮狀態。圖中可以看出串級控
制可以使系統對輸入的階躍信號有很快的響應時間,而且通過不斷調節控制器參數可以使系統達到預期的最佳目的。同時串級控制器可以使系統在追蹤輸入信號時更好地控制穩定,減小位移超調量,縮短反應時間,提高跟蹤能力。




圖4 階躍信號響應仿真結果
4 控制特性實驗驗證
4.1 實驗驗證方案
本實驗中,驅動盤狀永磁鐵的驅動電機選用日本HarmonicD公司生產的RH-5A8802型號的伺服電機,其參數為:額定電壓12 V,轉動慣量為6.37×10-4kg·m2,額定回轉速度為88 r/min,最高轉速為180 r/min。位移傳感器選用日本基恩士公司生產的電渦流位移傳感器EX-V系列。永磁體材料為釹鐵硼NdFeB30,與永磁體正對的“F”形導磁體材料為坡莫合金1J85。
4.2 控制特性的實驗結果分析
為進一步驗證懸浮可能性及系統響應特性,結合dSPACE控制器搭建可控磁路式永磁懸浮系統實驗裝置,系統穩定懸浮狀態如圖5所示。系統中,懸浮物由材質分別為坡莫合金和鐵的兩種長方體組成,把坡莫合金材質的懸浮物放在上面加強懸浮物的導磁效果,把鐵材質的懸浮物放在下面使傳感器檢測懸浮物的位置;本系統為單自由度系統,懸浮物通過直角板固定在滑塊上限定懸浮物只做豎直運動。懸浮實驗中,懸浮物內環控制器PD及外環控制器PID分別為kp1=460,kd1=0.8;kp2=400,ki2=2 000,kd2=0.2。

圖5 懸浮系統實驗裝置
實驗條件與上述仿真條件相同,采用上述串級控制器和圖3的控制系統結構,得到結果如圖6所示。
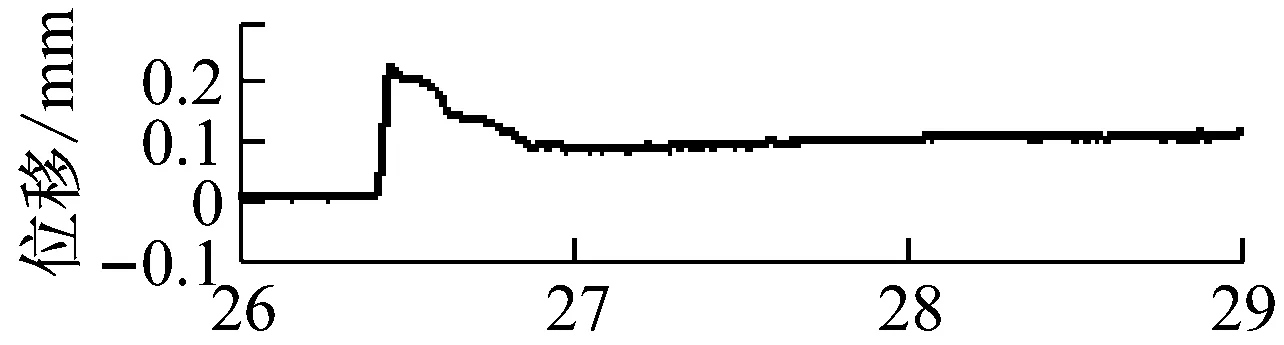

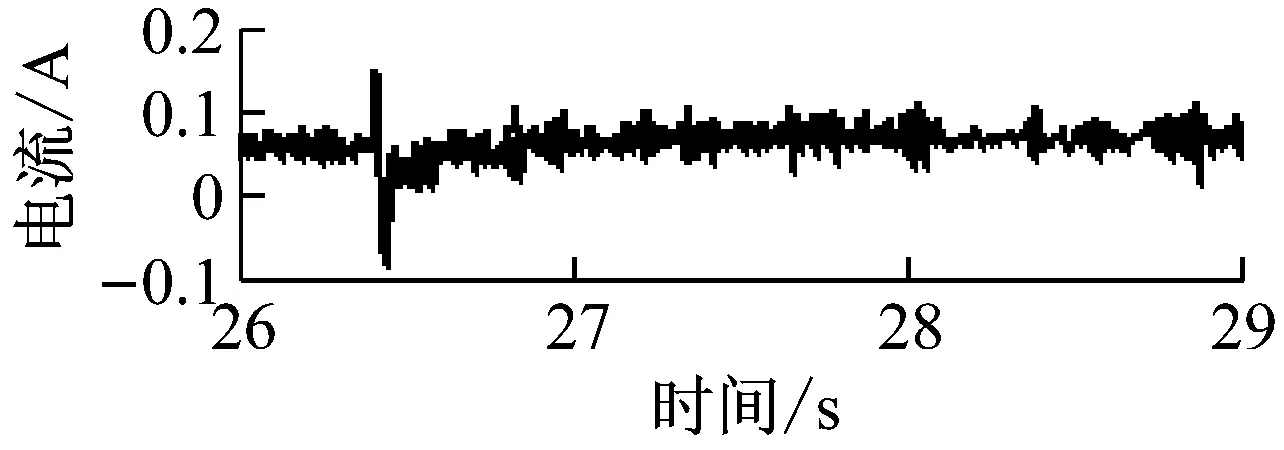
圖6 系統實驗階躍響應結果
實驗結果表明:在系統處于平衡狀態的情況下,給系統輸入一個0.1 mm階躍位移信號,經過串級控制,使懸浮物再次達到穩定懸浮狀態。圖中可以看出在輸入階躍的作用下,系統的振蕩加劇,響應加快,電流變化加快,但是經過調節器調節,系統最終穩定下來,同時因為實驗裝置存在直線導軌摩擦力的影響,實驗結果與仿真結果略有區別。串級控制器在輸入階躍位移實驗中也體現了控制的能力。
5 結 論
根據可控磁路式永磁懸浮系統所具有的自身特點,本文設計了一種由角度環和位置環組成的串級控制器。該控制器將可控磁路式永磁懸浮的四階系統降階成兩個二階系統,簡化了控制器的結構,降低了控制器的設計難度,使得高階系統的控制變得簡單化。同時使系統具有一定的抗干擾能力,能及時跟蹤輸入位移信號,快速達到系統穩定。仿真和實驗數據分析表明該串級控制器可以較好地控制系統的穩定,能夠實現懸浮物的穩定懸浮,在跟蹤輸入階躍信號中串級控制表現出了較好的穩定性和魯棒性,同時為了更好的驗證串級控制在該系統的控制性能,還需進一步優化實驗裝置,減小摩擦力對實驗的影響。
參 考 文 獻
[1] SUN F, OKA K. Development of noncontact suspension mechanism using flux path control disk magnet rotation[J]. Transactions of the Japan Society of Mechanical Engineers, 2010, 76(771): 2916-2922.
[2] OKA K. Noncontact manipulation with permanent magnet motion control[C]∥Proceeding of the 4th International Symposium on Linear Drivers for Industry Applications: Birmingham: CDROM, 2003: 259-262.
[3] 宋文榮,于國飛,王延風. 磁懸浮微進給機構的控制[J]. 哈爾濱工業大學學報, 2004, 36(1): 28-31.
SONG Wenrong,YU Guofei,WANG Yanfeng. PID control of micro feed mechanism based on magnetic levitation trchnology[J]. Journal of Harbin Institute of Technology, 2004, 36(1): 28-31.
[4] 劉恒坤,郝阿明,常文森. 磁懸浮系統的非線性PID控制[J]. 控制工程, 2007, 14(6): 653-656.
LIU Hengkun,HAO Aming,CHANG Wensen.Nonlinear PID control of magnetic suspensi on systems[J]. Control Engineering of China, 2007, 14(6): 653-656.
[5] 陳龍,陳建軍,張雪峰. 不確定結構振動的保成本魯棒PID控制[J]. 振動與沖擊, 2007, 26(6): 79-89.
CHEN Long,CHEN Jianjun,ZHANG Xuefeng. Guaranteed cost robust PID control for uncertain structure vibration[J]. Journal of Vibration and Shock, 2007, 26(6):79-89.
[6] 李榮,焦曉紅,楊超. 基于動態輸出反饋的半車主動懸架系統魯棒控制[J]. 振動與沖擊, 2014, 33(7): 187-193.
LI Rong,JIAO Xiaohong,YANG Chao. Output feedback-based robust control for a half-car hydraulic active suspension syetem[J]. Journal of Vibration and Shock, 2014, 33(7): 187-193.
[7] 孫興偉,夏鵬澎,金俊杰,等. 可控磁路式永磁懸浮系統的模糊魯棒控制[J]. 組合機床與自動化加工技術, 2016, 2(2): 76-78.
SUN Xingwei,XIA Pengpeng,JIN Junjie,et al. Fuzzy robust control of permanent magnetic suspension system using variable flux path control method[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016, 2(2): 76-48.
[8] 舒光偉,REINHOLD M. 基于Simulink的磁懸浮控制系統仿真[J]. 系統仿真學報, 2008, 20(8): 2168-2171.
SHU Guangwei,REINHOLD M. Simulation of magnetic suspension control system based on simulink[J]. Journal of System Simulation, 2008, 20(8): 2168-2171.
[9] 申愷,孫純祥. 主動磁懸浮系統的MATLAB仿真研究[J]. 工業儀表與自動化裝置, 2008, 4: 7-10.
SHEN Kai,SUN Chunxiang. Research on an active magnetic suspension system with matlab simulation[J]. Industrial Instrumentation & Automation, 2008, 4:7-10.
[10] 周瑾,倪佐僖. 基于不平衡響應的磁懸浮軸承剛度阻尼辨識方法研究[J]. 振動與沖擊, 2013, 23(3): 29-34.
ZHOU Jin,NI Zuoxi. Identification method for stiffness and damping of magnetic bearings on rotor unbalance responses[J]. Journal of Vibration and Shock, 2013, 23(3): 29-34.

