一種改進的Stewart平臺Newton-Euler動力學模型

何兆麒， 薛冬新， 張 娟， 宋希庚

(1. 大連理工大學 能源與動力學院， 遼寧 大連 116024; 2. 大連裝備職業技術學院 航海工程系， 遼寧 大連 116024)

自1965年，Stewart[1]發表了最早的將并聯機構用作飛行模擬器的文章以來，由于結構剛度大、承載能力強、誤差小、精度高、動力性能好等一系列優點，并聯機構在空間對接、并聯機床、隔振、高精密平臺等方面得到廣泛應用[2-12]。但因并聯平臺是閉環多剛體結構，使得運動學正解、動力學分析更加復雜。目前，用于Stewart平臺的動力學建模方法主要有牛頓-歐拉法、Lagrange法、虛功原理以及Kane法等。其中Newton-Euler法是由牛頓第二定律直接推導出來的，方法直觀，應用廣泛。Fichter在忽略運動支鏈的質量和鉸鏈摩擦的情況下，給出了平臺驅動與慣性力以及外力之間的關系。Do等[3]基于Newton-Euler法建立了忽略關節摩擦和支腿軸向轉動慣量時Stewart并聯機構的逆動力學模型。Dasgupta等在充分考慮Stewart動平臺慣性、支腿慣性和關節摩擦的基礎上，提出了較為完善的Newton-Euler閉環動力模型(下文以經典模型指代)，在此后的研究中得到廣泛的應用。但逐漸有學者指出，該經典模型存在幾點不足，① 忽略了支腿繞其自身軸線的回轉運動；② 假設萬向鉸處的約束力矩沿著支桿方向；③ 計算各結構的轉動慣量時沒有正確考慮平行軸定理。雖然以上這些假設簡化了模型，提高了計算效率，但這些假設不符合實際，會降低模型的準確性。李長春等[13]提出一種考慮支腿轉動的逆動力學模型，通過算例比較了忽略支腿繞自身轉軸轉動對運動學逆解的影響。Fu等[14-15]從不同的方面給出了修改建議，郭洪波[16]從能量的角度分析了忽略支腿繞自身軸線的回轉運動對動力學模型的影響。Pedrammehr等[17]綜合上述三方面，建立了改進的牛頓-歐拉動力學模型，逆動力學計算結果表明改進模型與Dasgupta的經典模型有明顯的不同。

由理論力學的相關知識可知，利用轉動慣量表示剛體的動量矩時，矩心是否為剛體固連點，將影響動量矩定理的具體表述形式。建立Stewart平臺的動力學模型時，通常將單個支腿簡化為上、下支桿，分別關于下鉸點取矩。下支桿受力關于下鉸點的力矩平衡可認為是對剛體固連點取矩，而上支桿受力對下鉸點的力矩平衡是對剛體外一點取矩，兩者應做不同處理。但以往的研究忽略了這一點，因此，筆者認為經典模型除了以上三點不足外，還存在以下問題，即：在建立支腿和動平臺的歐拉方程時，沒有合理區分力矩簡化中心是否固連于剛體。基于這一考慮，筆者在文獻[18]僅針對上支桿歐拉方程的建立，給出了修改建議。本文首先闡述改進工作的理論依據，其次針對6-UPS型Stewart平臺，在前人研究成果的基礎上，區分矩心是否為剛體固連點，在第2、3節分別建立利用非質心轉動慣量和質心轉動慣量表示的兩種改進閉環動力學模型。最后通過求解文獻[4]的算例，比較本文改進模型和經典模型動態響應的不同，說明改進的必要性。

1 理論依據

如圖1所示，以O0為原點建立慣性坐標系O0x0y0z0，C是剛體質心，B點相對于慣性系作任意運動，關于動點的動量矩定理可表示為

(1)

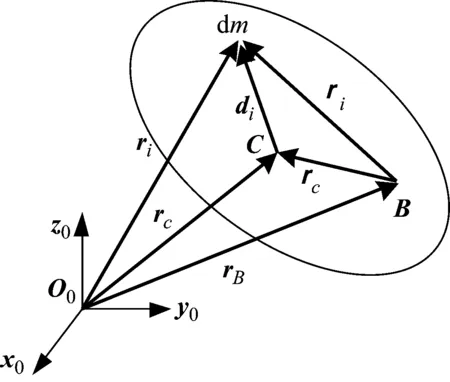
圖1 剛體上質量微元dm的矢量表示

(2)

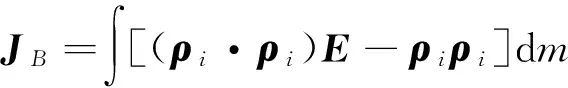
將式(2)代入式(1)得

(3)

當點B靜止時，式(3)變為

(4)

(5)

當B點固定時，式(5)仍然成立。

下文中為敘述方便，將式(3)稱為依據一，式(5)稱為依據二。

2 6-UPS型Stewart平臺動力學分析

本文所研究的Stewart平臺結構及第i支桿矢量表示如圖2所示。下平臺固定，連桿與上、下平臺分別采用球鉸、萬向鉸連接，支桿為直線運動副，機構具有六個運動自由度。上、下平臺六個鉸鏈點中心分別為Pi、Bi(i=1,…,6)。為便于運動學和動力學分析，在上、下平臺的幾何中心點P、B處建立連體坐標系{PX1Y1Z1}、參考坐標系{BXYZ}。

圖2 Stewart平臺及第i支桿矢量圖

以下符號被用于平臺建模中：tp為上平臺參考點P在{B}中的位置矢量；ωp,αp為上平臺角速度、角加速度；Rp為RPY角描述的上平臺的旋轉變換矩陣；pi為上平臺各球鉸鉸心Pi在{P}中的位置矢量；bi為下平臺各萬向鉸鉸心Bi在{B}中的位置矢量；Si為鉸心Bi到對應Pi在{B}中的位置矢量；ei為第i根支桿單位矢量；ωli,αli為第i根支桿的角速度、角加速度；Iu0i,Id0i為上下支桿在各自質心坐標系(坐標原點在上下支桿質心處，方向與{D}相同)的慣量矩陣；Ip0：上平臺和質量負載在質心坐標系(原點在上平臺綜合質心，方向與{P}相同)的慣量矩陣。

2.1 第i個支桿運動學分析

在Pi、Bi處建立上、下支桿局部坐標系{U}、{D}，坐標系{D}的x軸沿支桿方向，y軸沿萬向鉸軸線方向，z軸由右手定則確定，{U}各軸與{D}相應的軸線平行。此外，在Bi處還有支腿固定坐標系{BiXBiYBiZBi}，方向與{B}平行。

(1) 上平臺鉸接點速度、加速度分析

由圖2可知，第i支桿的位置矢量

Si=tp+Rppi-bi=tp+qi-bi

(6)

則支桿長度和沿支桿單位矢量可以表示為

(7)

ei=Si/Li

(8)

對式(6)兩端微分，得點Pi的速度、加速度為

(9)

(10)

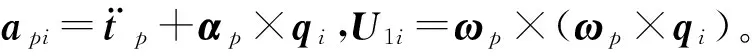
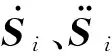
(11)

(12)

(2) 支桿滑動速度、加速度分析

由式(11)、式(12)，結合式(10)整理得支桿伸縮速度、伸縮加速度分別為

(13)

(14)

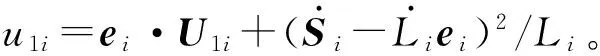
(3) 支桿角速度ωli、角加速度αli分析

如圖3所示，單位向量ki、yi、hi代表第i個萬向鉸模型，ki沿著萬向鉸的固定軸，yi沿著萬向鉸的旋轉軸，hi垂直于ki、yi組成的平面。由結構特點知，yi與ki共面且相互垂直，與支桿單位向量ei也相互垂直，xi、yi、zi代表上文的坐標系{D}。因此，從{D}～{BiXBiYBiZBi}的旋轉變換矩陣為

Ti=[xi,yi,zi]

(15)

由運動學約束知，ωli位于ki、yi組成的平面內

ωli=ωkiki+ωyiyi

(16)

式中：ωki、ωyi分別為支桿角速度沿著ki、yi的分量。

圖3 萬向鉸結構簡圖

文獻[4-5]假設支桿角速度ωli⊥ei，即要求支桿垂直于ki、yi組成的平面。由結構特點知，這就要求必須忽略支桿繞自身軸線的旋轉自由度，顯然這不符合實際，因此假設ωli⊥ei是不合理的。

將式(16)代入式(11)，整理得

(17)

(18)

對式(16)兩端求導，支桿角加速度αli表示為

αli=αkiki+αyiyi+ωyiωkihi

(19)

此外，ωli還可以分解為垂直于支桿的分量ω和沿著支桿方向的分量ωeiei，即

ωli=ω+ωeiei

(20)

將式(20)代入式(11)，可得到

(21)

因ωli位于ki、yi組成的平面內，而hi垂直于該平面，所以ωli·hi=0。利用這一性質，由式(20)得

ωei=-(ω·hi)/(ei·hi)

(22)

同樣，αli可以分解為垂直于支桿的分量α和沿著支桿方向的分量αeiei，即

αli=α+αeiei

(23)

將式(23)代入式(12)，整理得

α=(ei×api)/Li+U2i

(24)

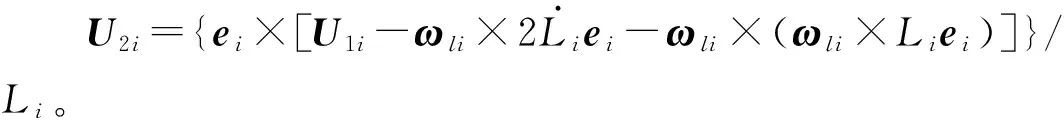
由式(23)和式(19)整理得

αki=(α+αeiei)·ki

(25)

αei=[(α·ki)ki·ei+ωyiωkihi·ei]/1-

(26)

至此，將式(24)、式(26)代入式(23)得到支桿角加速度的完整表達

u2iei

(27)

(4) 上、下支桿質心速度、加速度分析

上、下支桿質心(圖2中的Gu、Gd)在{BiXBiYBiZBi}的位置矢量rui、rdi可表示為

rui=Ti(vi+ru0i)

(28)

rdi=Tird0i

(29)

因此，上、下支桿質心的加速度可分別表示為

(30)

(31)

2.2 第i個支桿動力學分析

應用平行軸定理，上下支桿對點Bi的慣量矩陣為

圖4是單個運動支鏈的受力簡圖，Fsi是球鉸處約束力，Cu和Cs是萬向鉸和球鉸處的黏性阻尼系數。Fui、Mui分別為萬向鉸處的約束力矢量和約束力矩幅值。因為萬向鉸在yi、ki兩個方向上有旋轉自由度，約束力矩只能沿著hi方向，因此約束力矩為Muihi，而不是經典模型中的Muiei。

圖4 第i個支桿受力分析示意圖

根據第1節中依據一，結合受力分析，建立整個支桿關于Bi點的歐拉方程

-rui×muaDi+(mdrdi+murui)×g-(Idi+Iui)αli-

ωli×(Idi+Iui)ωli+Muihi+Si×Fsi-Cuωli-

fi=0

(32)

式中：fi=Cs(ωli-ωp)為球絞摩擦力矩；aDi為該瞬時，上支桿上與Bi點相重合的點的絕對加速度。

由運動學分析知

(33)

將式(14)代入式(33)整理得

aDi=(ei·api)ei+U3i

(34)

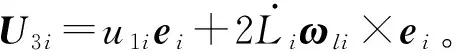
將式(32)改寫為

Muihi+Si×Fsi=Ni

(35)

其中,

Ni=rui×muaDi-(mdrdi+murui)×g+

(Idi+Iui)αli+ωli×(Idi+Iui)ωli+Cuωli+fi

(36)

式(35)兩端點乘、叉乘ei，得到Mui及Fsi為

Mui=(Ni·ei)/(hi·ei)

(37)

Fsi=ei(ei·Fsi)+(Ni×ei-Muihi×ei)/Li

(38)

為了得到(ei·Fsi)，考慮上支桿沿支桿方向的受力平衡

(39)

式中：Facti、Cp分別為滑移鉸處支桿主動力、黏性摩擦因數。

將式(37)、式(39)代入式(38)整理得

(40)

將式(36)代入式(40)，利用式(30)、式(14)、式(23)、式(33)，并結合矢量計算規則化簡Fsi的表達式

(41)

其中

U4i=u1iei+U2i×rui+ωli×(ωli×rui)；

U5i=mu(rui×U3i)+(Idi+Iui)(U2i+u2iei)-

(mdrdi+murui)×g+ωli×(Idi+Iui)ωli+Cuωli+fi；

為了推導式(41)，需要用到以下矢量代數運算規則

(a·b)c=(aTb)c=c(aTb)

2.3 上平臺運動學、動力學分析

上平臺和質量負載的綜合質心在{B}中的位置矢量表示為

qc=tp+RpR0=tp+R

(42)

式中：R0為上平臺和質量負載的綜合質心在{P}中的位置矢量。

對式(42)進行微分，得到綜合質心的加速度

(43)

由平行軸定理，上平臺和質量負載對點P的轉動慣量為

(44)

式中：mp為上平臺和質量負載的質量之和。

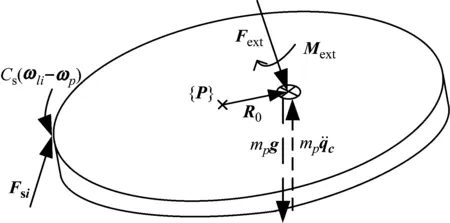
圖5 上平臺受力分析簡圖

上平臺的牛頓方程、相對點P的歐拉方程分別為

(45)

(46)

式中：Fext,Mext分別為外界作用于上平臺的作用力和作用力矩在局部坐標系{P}中的表示。

將式(43)、式(41)代入式(45)、式(46)進行整理

(47)

(48)

合并式(47)、式(48)，得到上平臺的完整動力學方程

(49)

其中，

H=

3 質心轉動慣量表示的6-UPS Stewart平臺閉環動力學方程

文獻[4-5]建立的歐拉方程，包含了質心加速度項，如果從這一角度推導方程，則方程中轉動慣量項的計算需要做出調整。為了評估此誤差，本節以第1節的依據二為基礎，利用質心轉動慣量建立動力學模型。這種表述形式下，對支桿和上平臺的運動學分析同2.1、2.3，不同在于各結構動力學方程的建立。

第i個支桿關于Bi點的歐拉方程為

(Idci+Iuci)αli-ωli×(Idci+Iuci)ωli+

Muihi+Si×Fsi-Cuωli-fi=0

(50)

采用同式(32)類似的簡化運算，得到

(51)

其中,

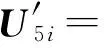
(Idci+Iuci)(U2i+u2iei)

u1i,U2i,u2i的表達式同第2節。

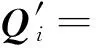
上平臺和質量負載關于質心坐標系(原點在綜合質心，方向與{B}相同)的轉動慣量為

(52)

考慮上平臺相對點P的力矩平衡

(53)

將式(43)、式(51)代入式(53)進行整理

mpR×[ωp×(ωp×R)-g]+ωp×Ipcωp+

(54)

合并式(47)、式(54)，得到上平臺的完整動力學方程

(55)

其中，

4 計算實例

為了比較改進模型與原模型的不同，筆者利用兩種改進形式的Stewart平臺完整動力學模型式(49)、式(55)求解文獻[4]的計算實例，并與原文的結果進行比較。Stewart平臺的結構參數、初始條件見附錄2。

同經典模型一樣，采用基于任務空間運動狀態反饋的PD控制算法求解支桿主動力，PD算法描述如下

(56)

式中：Kp=[4.0×1054.0×1054.0×1065.0×1045.0×1041.0×105]T;Kd=[1.0×1041.0×1042.0×1041.0×1031.0×1032.0×103]T。

4.1 第一種改進模型式與經典模型比較

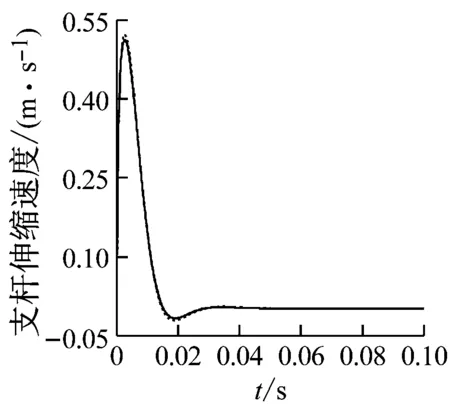
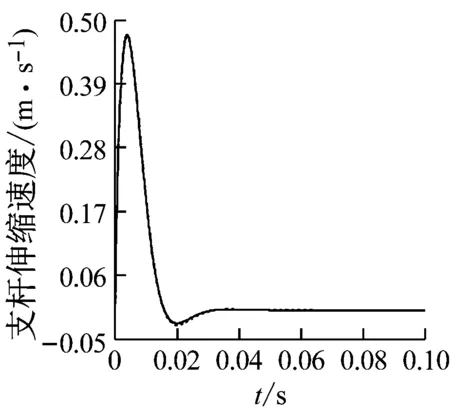
根據式(49)求解支桿長度、伸縮速度和上平臺位移、速度的響應曲線，并與原模型計算結果一起顯示在圖6～圖9中，所有圖中實線、虛線分別為改進模型、原模型的響應結果。圖6、圖7的第一張小圖右上角展示了Leg1長度和運動速度變化的局部放大曲線。可以觀察到響應曲線的初始階段及峰值處，兩種模型下Leg1的長度和速度值略有不同，其余支桿也呈現類似的情況。

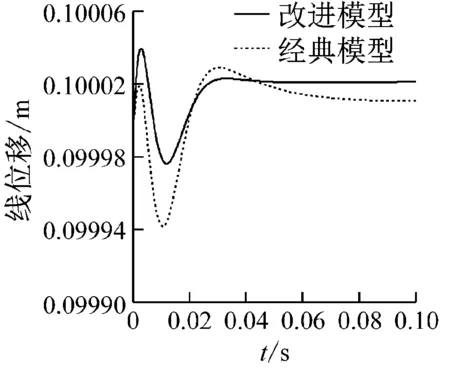
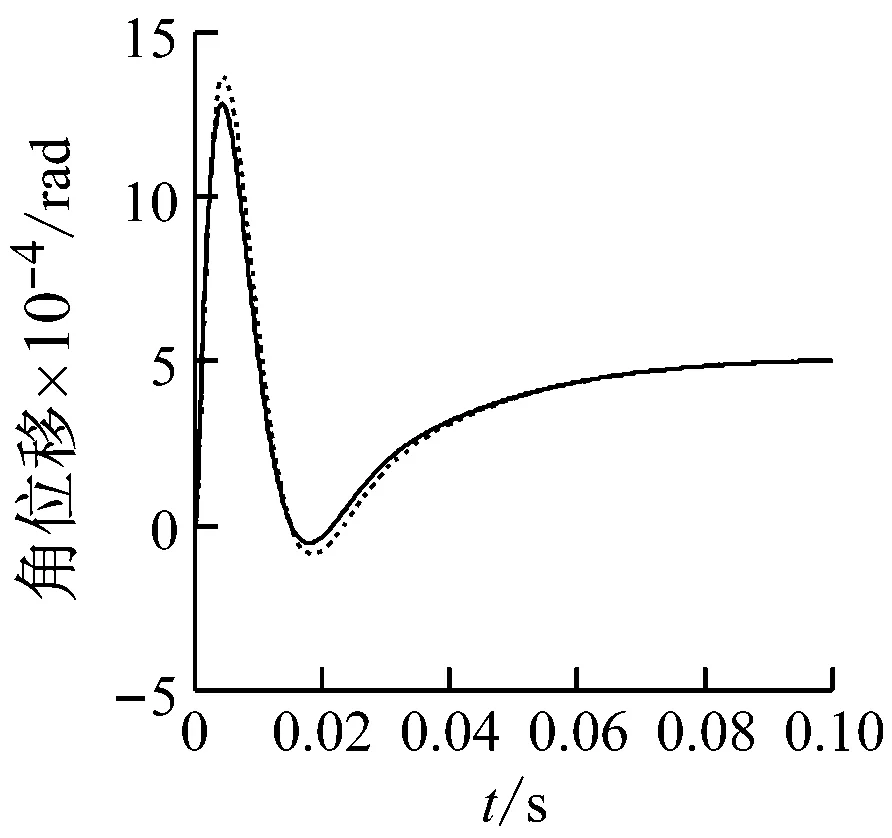
同樣，由圖8和圖9可見，改進模型、原模型求解得到的上平臺位移、速度、轉角、角速度都具有相似的變化趨勢，但幅值不同。由于初始狀態和期望狀態線位移tp、角位移θp的X、Y方向分量為0，因此兩模型在這兩個方向上的差值數量級很低。而速度響應在峰值處差值較為明顯。圖10描述了6根支桿所需的主動力，每個圖中的小圖描述了兩種模型的差值，峰值處最大的誤差值達到了45.94%。所以，從整體上來看，改進模型和原模型所有運動參數具有相似的變化趨勢，但在峰值處，幅值呈現較為明顯的不同。

4.2 第二種改進模型式與經典模型比較

經計算，由(55)得到的響應曲線與第一種改進形式(49)的結果完全一致，因此，第二種改進模型式(56)與經典模型的比較同圖6～圖10。由于篇幅有限，此處不再展示。實際上，第1節中的依據一、二本質上是一樣的，它們是動量矩定理的兩種不同表述。因此，以此為基礎得到的兩種改進形式本質上也是一致的。

5 結 論

本文在考慮支桿繞自身軸線的旋轉自由度、修正萬向鉸約束力矩、合理應用平行軸定理計算各部分轉動慣量、正確利用動量矩定理建立支桿及平臺的歐拉方程的基礎上，對原有基于Newton-Euler法建立的Stewart平臺經典閉環動力學模型進行改進。得到質心轉動慣量和非質心轉動慣量表示的兩種不同形式改進模型，這兩種模型從本質上是一致的，計算結果很好的說明了這一點。

此外，從改進模型與原模型的計算結果比較來看，所有參數變化趨勢相同，但所有時間點的響應呈現不同程度的誤差，尤其是曲線峰值處。由于算例中設置的初始條件和期望狀態的差值很小，而且整個Stewart平臺結構尺寸、重量也較小，因此最終的比較結果并沒有表現出特別顯著的不同。從理論推導的角度來看，改進模型雖然只是對方程中某些項做了的修正，但提高了模型的準確性。對大型的平臺結構這些修正帶來的影響可能會更顯著，因此改進工作是很有必要的，對后期的研究具有重要意義。

(a) Leg 1

(b) Leg 2

(c) Leg 3

(d) Leg 4

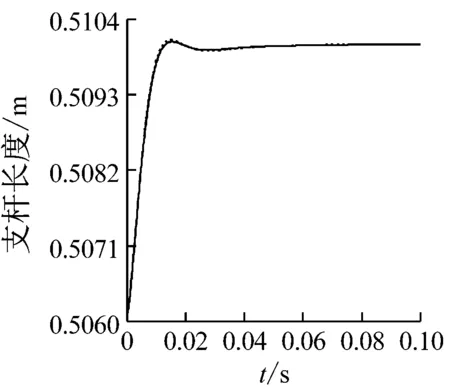
(e) Leg 5

(f) Leg 6

圖6 支桿長度隨時間變化曲線

Fig.6 Time response curve of pod length

(a) Leg 1

(b) Leg 2

(c) Leg 3

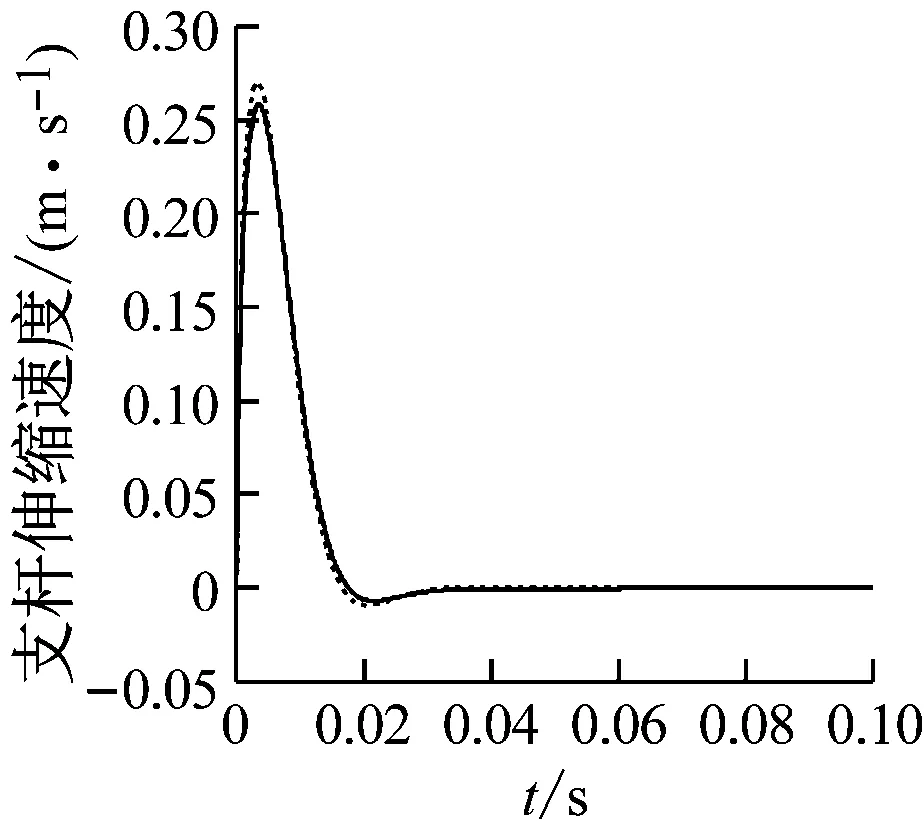
(d) Leg 4

(e) Leg 5

(f) Leg 6

圖7 支桿速度的時間響應曲線

Fig.7 Time response curve of pod velocity

(a)X

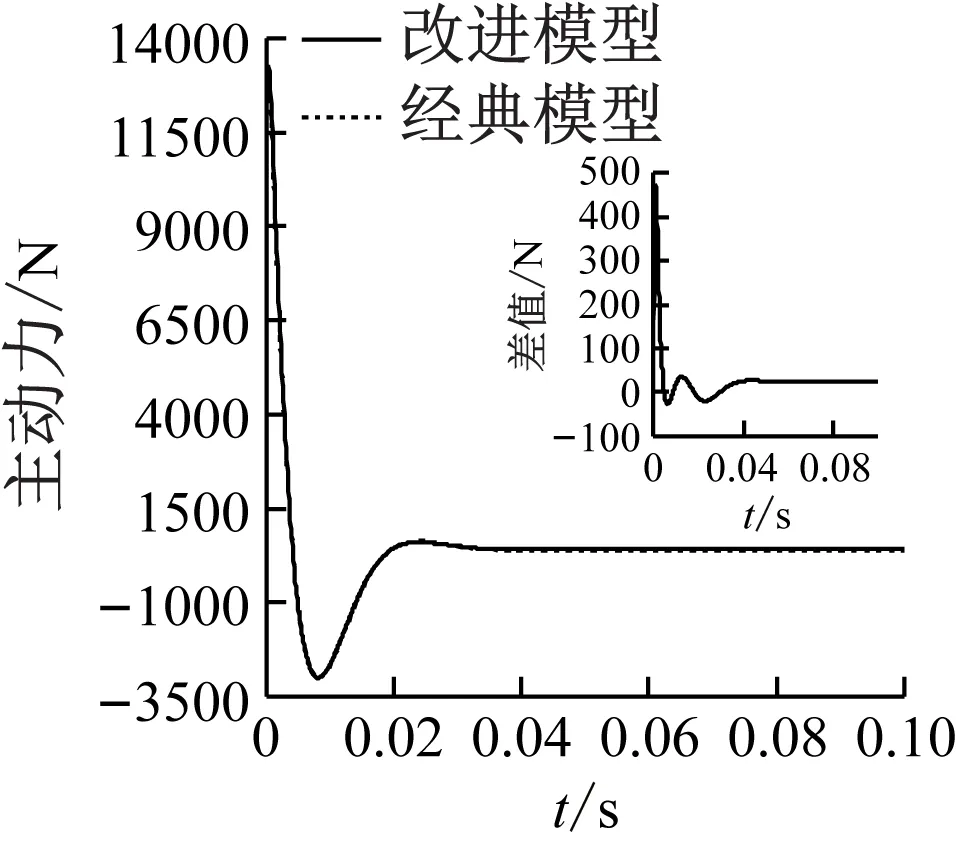
(a) Leg 1

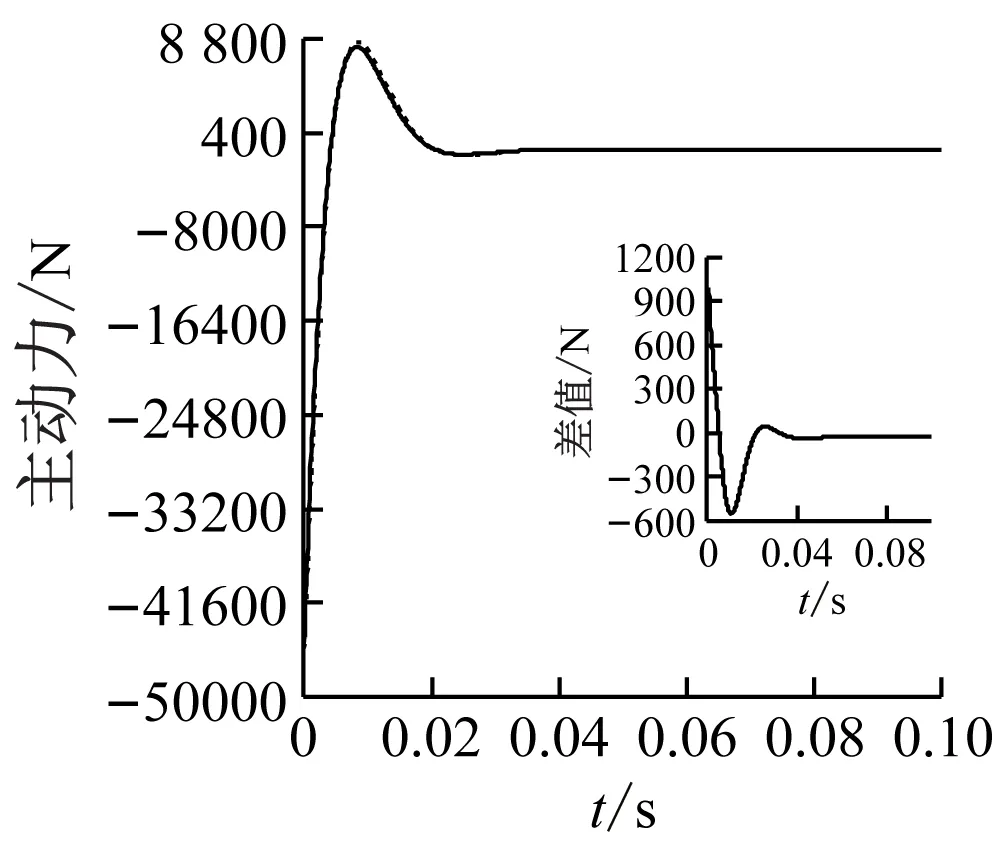
(b) Leg 2

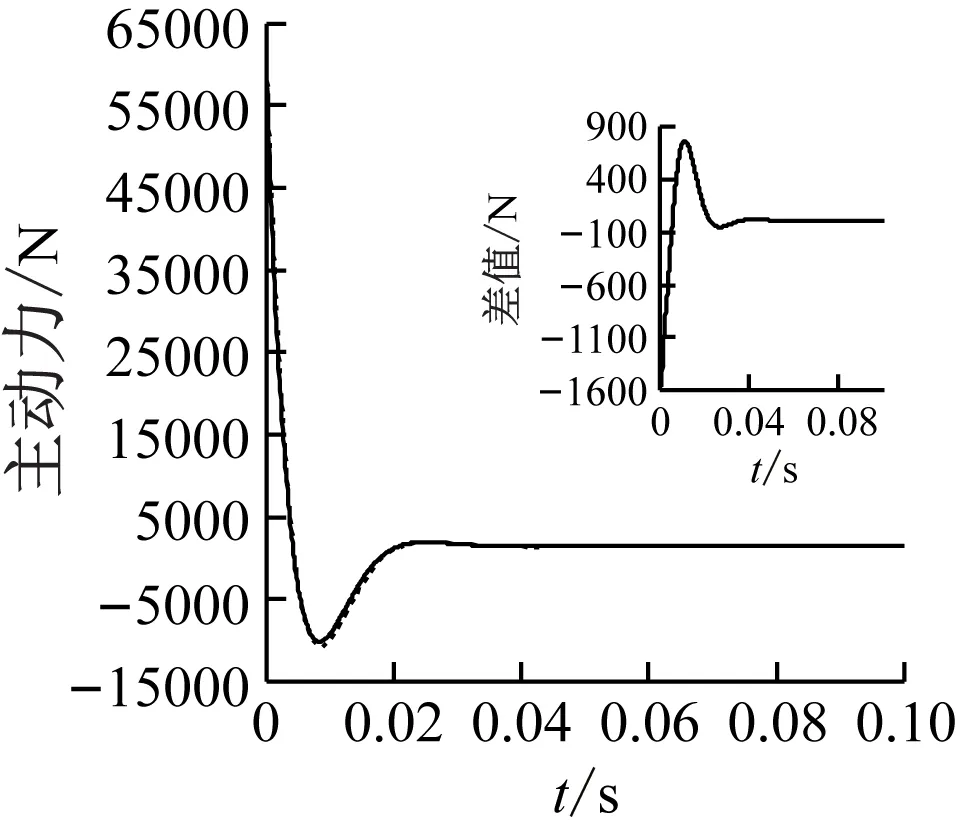
(c) Leg 3

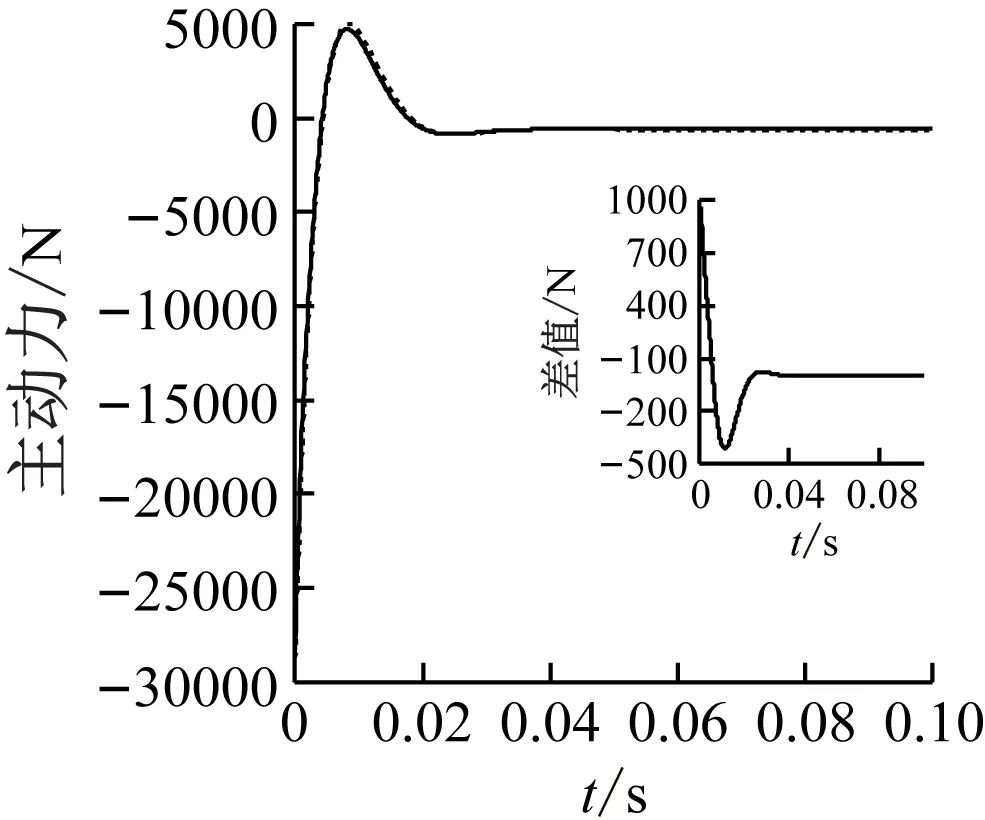
(d) Leg 4

(e) Leg 5

(f) Leg 6

參 考 文 獻

[1] STEWART D. A platform with six degrees of freedom[J]. Proceedings of the Institution of Mechanical Engineers, 1965, 180(1): 371-386.

[2] FICHTER E F. A stewart platform-based manipulator: general theory and practical construction[J]. The International Journal of Robotics Research, 1986, 5(2): 157-182.

[3] DO W Q D, YANG D C H. Inverse dynamic analysis and simulation of a platform type of robot[J]. Journal of Robotic Systems, 1988, 5(3): 209-227.

[4] DASGUPTA B, MRUTHYUNJAYA T S. Closed-form dynamic equations of the general Stewart platform through the Newton-Euler approach[J]. Mechanism and Machine Theory, 1998, 33(7): 993-1012.

[5] DASGUPTA B, MRUTHYUNJAYA T S. A Newton-Euler formulation for the inverse dynamics of the stewart platform manipulator[J]. Mechanism and Machine Theory, 1998, 33(8): 1135-1152.

[6] LEE K M, SHAH D K. Dynamic analysis of a three-degrees-of-freedom in-parallel actuated manipulator[J]. IEEE Journal on Robotics and Automation, 1988, 4(3): 361-367.

[7] YANG J, GENG Z J. Closed form forward kinematics solution to a class of hexapod robots[J]. IEEE Transactions on Robotics and Automation, 1998, 14(3): 503-508.

[8] WANG J, GOSSELIN C M. A new approach for the dynamic analysis of parallel manipulators[J]. Multibody System Dynamics, 1998, 2(3): 317-334.

[9] TSAI L W. Solving the inverse dynamics of a Stewart-Gough manipulator by the principle of virtual work[J]. Journal of Mechanical Design, 2000, 122(1): 3-9.

[10] LIU M J, LI C X, LI C N. Dynamics analysis of the Gough-Stewart platform manipulator[J]. IEEE Transactions on Robotics and Automation, 2000, 16(1): 94-98.

[11] 羅波,李偉鵬,黃海.基于Stewart平臺的大柔性空間桁架結構振動控制[J]. 振動與沖擊, 2012,31(23):148-153.

LUO Bo,LI Weipeng,HUANG Hai. Vibration control of a large flexible space truss using a Stewart platform manipulator[J]. Journal of Vibration and Shock, 2012,31(23):148-153.

[12] 李喬博,王超新,黃修長，等. 基于Stewart平臺微振動主動控制分析與實驗[J].噪聲與振動控制， 2016,36(3):214-218.

LI Qiaobo, WANG Chaoxin, HUANG Xiuchang, et al. Analysis and experiment of micro-vibration active control based on a stewart platform[J]. Noise and Vibration Control, 2016,36(3):214-218.

[13] 李長春,延皓,張金英，等. 一種改進的6自由度運動模擬器逆動力學模型[J].兵工學報, 2009,30(4):446-450.

LI Changchun,YAN Hao,ZHANG Jinyin， et al. An improved inverse dynamics model of 6-DOF motion simulator[J]. Acta Armamentarii, 2009,30(4):446-450.

[14] FU S W, YAO Y. Comments on “A Newton-Euler formulation for the inverse dynamics of Stewart platform manipulator” by B. dasgupta and T.S. mruthyunjaya[mech. mach. theory 33 (1998) 1135-1152][J]. Mechanism and Machine Theory, 2007,42(12):1668-1671.

[15] VAKIL M, PENDAR H, ZOHOOR H. Comments to the:“Closed-form dynamic equations of the general Stewart platform through the Newton-Euler approach” and “A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator”[J]. Mechanism and Machine Theory, 2008,43(10): 1349-1351.

[16] 郭洪波. 液壓驅動六自由度平臺的動力學建模與控制[D]. 哈爾濱: 哈爾濱工業大學, 2006.

[17] PEDRAMMEHR S, MAHBOUBKHAH M, KHANI N. Improved dynamic equations for the generally configured Stewart platform manipulator[J]. Journal of Mechanical Science and Technology, 2012, 26(3): 711-721.

[18] HE Z, SONG X, XUE D. Comments to the:“Closed-form dynamic equations of the general Stewart platform through the Newton-Euler approach” and “A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator”[J]. Mechanism and Machine Theory, 2016, 102(10): 229-231.

[19] WITTENBURG J. Dynamics of multibody systems[M]. New York: Springer Science & Business Media, 2007.

附錄

Stewart平臺機構參數(均采用國際單位制)負載平臺(包括質量負載)的質量：mp=40.0； 上、下支腿的質量：mu=1.0，md=3.0；負載平臺(包括質量負載)的綜合質心在{P}的位置矢量：R0=[0.04 0.03 -0.06]T；上、下支腿的重心位置：ru0i=[-0.6 -0.08 0.08]T、rd0i=[0.4 0.14 -0.18]T；萬向鉸、柱鉸和球鉸的黏滯阻尼系數：Cu=0.000 1，Cp=0.001，Cs=0.000 2。

虎克鉸固定軸的單位矢量

k=

支桿上、下連接點的在各自局部坐標系的位置

上下支桿關于各自質心坐標系(坐標原點在上下支桿質心處，方向與{D}相同)的慣量矩陣

上平臺和質量負載在質心坐標系(原點在綜合質心，方向與{P}相同)的慣量矩陣

任務空間初始狀態和期望狀態

tp0=[0.1 0.0 0.395]T，θp0=[0.0 0.0 -0.2]T；

tpd=[0.1 0.0 0.4]T，θpd=[0.0 0.0 -0.2]T；

Fext=0，Mext=0。