剪式單元陣列可展結構的動力學分析方法

彭麒安， 王三民， 智常建， 李 博

(西北工業大學 機電學院，西安 710072)

可展結構是一種能夠像機構一樣運動，又能在鎖定后承受載荷、保持穩定構型的結構。與目前常見的其他結構不同的是，可展結構一般是由某一特定單元進行一定規則陣列組合而成，這是其區別于其他結構的顯著特點。隨著可展結構應用越來越廣泛，引發了許多學者的研究興趣。文獻[1-7]設計了各種新類型的可展結構，文獻[8-11]研究了可展結構作為機構時的運動學和動力學特性，文獻[12-15]則對其作為結構時靜力學問題進行了分析。文獻[16]雖然研究了可展結構的固有頻率，但使用的是傳統有限元方法，很難向大型陣列可展結構推廣。

隨著可展結構在航天領域深入應用，對其穩定性和振動要求越發嚴格，所以結構動力學成為了可展結構新的研究重點。但因其陣列單元數目過于龐大，難以用傳統有限元動力學分析方法進行分析，所以急需一種能夠快速簡單建立起動力學模型的方法。

本文以剪式單元平面陣列可展結構為研究對象，將通過對其單元特性矩陣進行規范化處理，使其疊加節點自由度與內部節點自由度分開，從而實現通過單元特性矩陣的首尾循環相加來獲得整體結構的剛度矩陣和質量矩陣，以提高建模效率，同時便于編程計算，并以此為基礎對可展結構進行動力學的分析，研究其固有頻率和動態響應等特性。因可展結構大部分具有陣列特性，故此方法也可推廣到其他單元類型的可展結構中。

1 剪式單元機構動力學模型與方程

剪式單元平面陣列可展結構如圖1 所示，可以看出它是由M層剪式單元線狀陣列可展結構拼接而成，而每層剪式單元線狀陣列又是由N個平面剪式單元可展結構組成，本文先對單個剪式單元進行研究，然后通過一定的方法進行組合最終得到復雜剪式單元面狀可展結構的相關特性。

圖1 剪式單元平面陣列可展結構

單個剪式單元機構如圖2所示，它是由兩個桿通過中間樞軸節點鉸接在一起的一個可展結構，展開角度用α表示。

一個剪式單元機構是由6個節點構成，分別為1,2,3,3′,4,5，其中3,3′是兩桿上各自的鉸接點，1,5和2,4分別是桿1和桿2兩端的端節點同時也是與外界相連的鉸節點。由于剪式單元的力學特性，在有限元分析中選用兩節點六自由度的梁單元進行分析，故此將剪式單元劃分成4個梁單元，分別為13,35,23′,3′4。

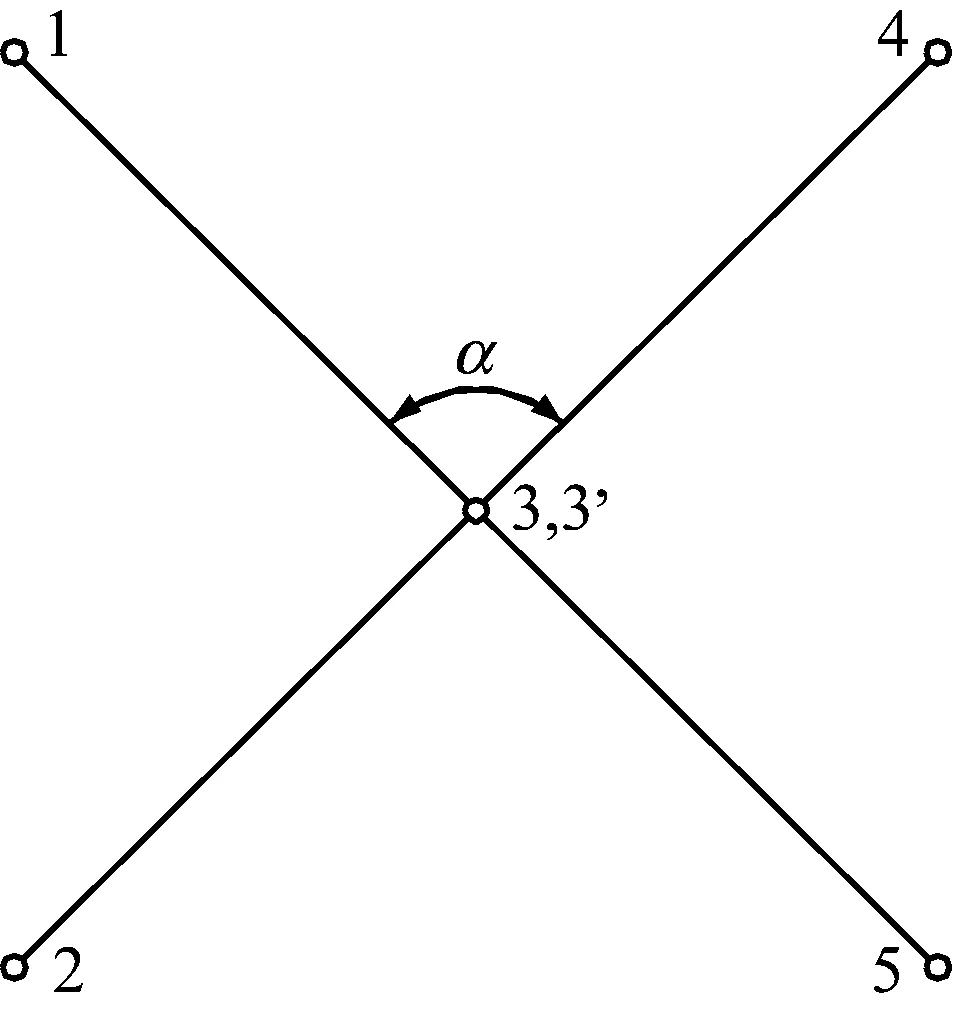
圖2 剪式單元機構

由有限元理論可知梁單元的質量矩陣和剛度矩陣分別為Me和Ke，坐標變換后利用主從自由度法約束鉸節點3,3′可得到剪式單元真實力學模型為

(1)

式中：Mr和Kr分別為剪式單元的質量矩陣和剛度矩陣;Cr為阻尼矩陣，在本文中均采用Rayleigh黏性比例阻尼模型;Pr為與時間相關的外載列陣。

2 陣列可展結構動力學分析方法

以圖2為例，剪式單元可展結構的節點位移為q=[u1,v1,θ1,u2,v2,θ2,u3,v3,θ3,θ3′,u4,v4,θ4,u5,v5,θ5]T，為了能夠實現前后兩個單元剛度矩陣和質量矩陣首尾相加，讓獨立的自由度不影響主從約束自由度的疊加，將節點位移列陣進行規范化

q′=Pq

(2)

式中:P為規范矩陣，規范化后的位移列陣為q′=[u1,v1,u2,v2,θ1,θ2,u3,v3,θ3,θ3′,θ4,θ5,u4,v4,u5,v5]T利用濾波法求解變換矩陣P，先假設變換矩陣P是一個全一矩陣，即為

現設置約束條件集為

(3)

式中i,j=1,2,3，…，16。

將其代入式(2)，則可以得到變換矩陣為P。得到變換矩陣后，即可求出變換過后的剛度矩陣為

KP=P·K·PT

(4)

再將其進行(N-1)次加法運算即可得到剪式單元線狀可展結構的剛度矩陣

式中：KH=Kaa+Kcc，Kaa和Kcc為疊加節點自由度對應的剛度矩陣;Kbb為內部節點自由度對應的剛度矩陣，其余矩陣為疊加節點自由度和內部節點自由度對應的耦合剛度矩陣。同理也可得質量矩陣MX。

再以剪式單元線狀陣列可展結構為子結構單元，進行規范化處理，N個剪式單元的線陣列可展結構節點位移列陣為

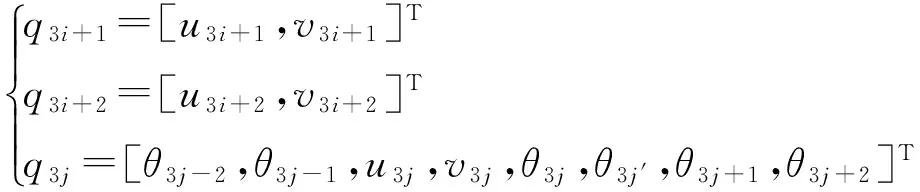
(5)

式中：i=0,1,2…n,j=1,2,…n。

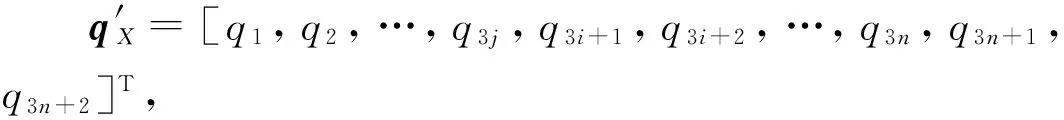
(6)

由此將其進行(M-1)次加法運算得到剪式單元面狀可展結構的剛度矩陣KM和質量矩陣MM。

故剪式單元平面陣列可展結構的動力學方程為

(7)

式中：MM、CM、KM、FM、qM分別為剪式單元平面陣列可展結構的質量矩陣、阻尼矩陣、剛度矩陣、與時間相關的廣義力向量和廣義位移向量。

因為可展結構在展開過程中應該避免發生共振，所以首先對其進行模態分析有

(8)

考慮到在工作狀態時，可展結構會受到變化的外載，對可展結構造成影響，因此還應該研究此時結構的動態響應

(9)

式中：MB,CB,KB,FB,qB分別為約束為結構后的平面陣列可展結構的質量矩陣、阻尼矩陣、剛度矩陣、與時間相關的外載列陣和位移列陣。

3 算 例

下面分析一個5×5的平面陣列可展結構的結構動力學，剪式單元個數N×M=25，桿件長度l=50 mm，橫截面寬b=3 mm，橫截面高h=4 mm，材料為空間中常用的鋁合金，其彈性模量E=71 GPa，密度ρ=2 770 kg/m3。根據以上條件求其動力學方程：由文獻[17]可知，按照傳統有限元方法需要對剪式單元的特性矩陣進行528次基本運算才能得到平面陣列剪式可展結構的特性矩陣；而按照本文方法只需對規范化后的矩陣進行16次加法運算就能得到可展結構的特性矩陣，運算次數僅為傳統方法的1/33，由此看來本文的規范法能夠大大提高建模效率。

3.1 模態分析

展開角度α=60°，通過編程得到固有頻率計算結果以及用ANSYS仿真計算結果(前12階)，將仿真計算結果作為標準，如表1所示。

表1 計算值與仿真值對比

從表1可以看出，無論是計算值還是仿真值前四階固有頻率都等于0，這是因為自由振動時，平面可展結構具有本身三個方向的剛體位移和一個運動的自由度導致的；另一方面，計算值與仿真值的最大誤差不超過0.04%，可以證明規范化方法的正確性。

依次計算展開角度α=0°～180°的固有頻率，結果如圖3所示。

圖3 5～12階固有頻率與展開角度關系

從圖3可以看出，當平面陣列可展結構展開角度發生變化時，它的固有頻率也會發生一定的改變，特別是在α=0°和α=180°這兩個極限位置附近，固有頻率突變并全部接近于0，說明這兩個位置結構不穩定，所以工作時應該避免這兩個位置，取頻率相對穩定的展角α=20°～160°。

3.2 動態響應

平面陣列可展結構工作狀態時約束和受力如圖4所示，此時展開角度α=45°，節點a處所受外載如圖5所示，分析其振動情況。

因加工方式的不同和微量元素的種類及含量的不同，鋁合金的阻尼系數有很大的不同，航天中常用的鋁合金的阻尼比可以分為三類：當近乎為純鋁時，此時阻尼很小可忽略不計，按無阻尼情況考慮，節點a處的響應如圖6所示，由于慣性的作用，結構會在平衡位置附近進行振動，且最大振幅為8.7×10-5m，在0.4 s卸掉外載后節點即以此時的偏移量為最大振幅圍繞新的平衡位置做周期振動，卸載前后周期一致；第二類是小阻尼鋁合金，通過查閱文獻[18]可知，某種鋁合金的阻尼比為0.056 5，此時響應如圖7所示，可以發現由外載導致的振動衰減很快，并且最大振幅減小為6.8×10-5m，僅為無阻尼時的78.2%；通過適當的阻尼增強處理，可將鋁合金的阻尼比增大到1.02，此時響應如圖8所示，可展結構將不再振動直接趨于平衡位置，且達到穩定的時間僅為前者的21%，故可以通過增大阻尼來減小外載帶給可展結構的振動影響。

圖4 可展結構工作狀態Fig.4 Deployablestructureworkingstate圖5 隨時間變化的外載Fig.5 Loadovertime圖6 無阻尼時點a橫向振動的位置響應曲線Fig.6 Non-dampingpointalateraloscillationposi-tionresponsecurve圖7 小阻尼時點a橫向振動的位置響應曲線Fig.7 Smalldampingpointalateraloscillationposi-tionresponsecurve

圖8 過阻尼時點a橫向振動的位置響應曲線

4 結 論

(1)本文基于有限元法提出了一種對剪式單元機構動力學分析的規范化方法。首先分析得到剪式單元的疊加節點自由度與內部節點自由度，然后將其分開并以此為規范化后的位移列陣，再通過濾波法求出此時的規范矩陣，用其對剪式單元特性矩陣進行了規范化，將規范化后的特性矩陣直接循環首尾相加組裝成平面陣列可展結構的剛度矩陣和質量矩陣，從而大幅度地降低了組裝難度，提高了建模效率，同時也為編程提供了便利。

(2)利用程序編程計算平面陣列可展結構的固有頻率并與ANSYS仿真結果進行比較，發現本方法計算值和仿真值最大誤差不超過0.04%，可以說明規范化方法的正確性。同時，利用程序計算了可展結構展開角度α=0°～180°的5～12階固有頻率，結果表明α=20°～160°時固有頻率是相對穩定的，機構應該在此區間內運動。

(3)針對平面陣列可展結構，進行了阻尼比為0(無阻尼)、0.056 5(小阻尼)和1.02(過阻尼)情況下的動態響應分析。當有阻尼時，外載變化引起的振動衰減很快，其中小阻尼時最大振幅僅為無阻尼時的78.2%，過阻尼時將不再發生振動，且到達穩定的時間僅為小阻尼時的21%，故可通過適當的增大阻尼來有效地減小結構振動。

參 考 文 獻

[1] LANGBECKER T J. Kinematic analysis of deployable scissor structures[J]. International Journal of Space Structures,1999,14(1):1-15.

[2] CHERNIAVSKY A G, GULYAYEV V I, GAIDAICHUK V V, et al. Large deployable space antennas based on usage of polygonal pantograph[J]. Journal of Aerospace Engineering, 2005, 18(3):139-145.

[3] TAGAWA H, SUGIURA N, KODAMA S. Structural analysis of deployable structure with scissor-like-element in architectural design class[C]∥ IABSE Symposium Report. Nara: IABSE, 2015.

[4] 陳向陽, 關富玲, 陳務軍,等. 復雜剪式鉸結構的幾何分析和設計[J]. 空間結構, 1998,4(1):45-51.

CHEN Xiangyang, GUAN Fuling, CHEN Wujun, et al. Geometry design and analysis of complex pantograph structures[J]. Spatial Structures, 1998,4(1): 45-51.

[5] 宋依潔, 熊海貝, 卿紫菲,等. 一種新型可展結構的探索[J]. 結構工程師, 2015, 31(5):48-53.

SONG Yijie, XIONG Haibei, QING Zifei, et al. Design and application of a new deployable structure[J]. Structural Engineers, 2015, 31(5): 48-53.

[6] 李慶營. 剪式鉸可展結構力學性能分析[D]. 南京:東南大學, 2012.

[7] 陳耀. 新型對稱可展結構的形態及展開過程分析與應用研究[D]. 南京:東南大學, 2014.

[8] ZHAO J, FENG Z, CHU F, et al. Chapter 11-mechanism theory and application of deployable structures based on scissor-like elements[J]. Advanced Theory of Constraint & Motion Analysis for Robot Mechanisms,2014:349-366.

[9] SUN Y, WANG S, MILLS J K. Kinematics and dynamics of deployable structures with scissor-like-elements based on screw theory[J]. Chinese Journal of Mechanical Engineering, 2014, 27(4):655-662.

[10] 紀斌, 王懷磊, 金棟平. 非對稱平面剪鉸結構展開過程分析與仿真[J]. 工程力學, 2013,30(7):7-13.

JI Bin, WANG Huailei, JIN Dongping. Analysis and simulation of the deployment process for asymmetric planar scissor structures[J]. Engineering Mechanics, 2013,30(7):7-13.

[11] 孫宏圖, 袁茹, 王三民. 正方形可展機構的運動學與動力學特性研究[J]. 西北工業大學學報, 2013,31(4):620-623.

SUN Hongtu, YUAN Ru, WANG Sanmin. Kinematics and dynamics characteristics of square developable structure[J]. Journal of Northwestern Polytechnical University, 2013,31(4):620-623.

[12] SHAN W. Computer analysis of foldable structures[J]. Computers & Structures, 1992, 42(6):903-912.

[13] 楊毅, 丁希侖. 剪式單元可展機構靜力學分析與拓撲優化設計[J]. 中國機械工程, 2010,21(2):184-189.

YANG Yi, DING Xilun. Analysis and topology optimization of deployable mechanism based on pantograph[J]. China Mechanical Engineering, 2010, 21(2):184-189.

[14] 劉國林, 王三民, 尚鵬. 剪式機構陣列可展結構的靜力學分析方法與應用研究[J]. 中國機械工程, 2014,25(4):461-466.

LIU Guolin, WANG Sanmin, SHANG Peng. Static analysis method and application research of line array deployable structures based on SLE[J]. China Mechanical Engineering, 2014, 25(4):461-466.

[15] 戴云景, 方有亮. 可展索-桁架結構的有限元分析[J]. 科學技術與工程, 2007, 7(4):538-541.

DAI Yunjing, FANG Youliang. Finite element analysis of deployable cable-truss structures[J]. Science Technology & Engineering, 2007,7(4):538-541.

[16] 劉樹青, 王興松, 朱正龍. 一種剪式可展結構設計與動力學分析[J]. 機械設計, 2011, 28(10):55-60.

LIU Shuqing, WANG Xingsong, ZHU Zhenglong. Design and dynamic analysis of a scissor deployable structure[J]. Journal of Machine Design, 2011, 28(10):55-60.

[17] 曾攀. 有限元分析及應用[M]. 北京:清華大學出版社, 2004.

[18] 王莉.幾種鋁合金的力學性能及阻尼特性[J].輕合金加工技術,2005,33(12):48-50.

WANG Li. Influence of aging on mechanical properties and damping behavior of several aluminium alloy[J]. Light Alloy Fabrication Technology,2005,33(12):48-50.