考慮參數不確定性的板結構振動響應統計分析
張艾萍, 李亞軒, 肖 斌, 石雙霞, 曹麗華, 高 超, 邱 瑞
(1.東北電力大學 能源與動力工程學院,吉林 吉林 132012;2.中國電力工程顧問集團 東北電力設計院有限公司,長春 130021)
實際工程結構中,由于系統參數、外部激勵以及邊界條件等一系列不確定性因素,致使系統的固有特性、動態響應與頻響特性等[1-3]具有隨機性特征。隨著工程中向復雜化和高精度方向的飛速發展,傳統上忽略或簡化這些因素的確定性結構分析方法,不再能滿足客觀要求,因此有必要將其納入到系統響應分析過程中。
近年來針對結構振動的動力學分析[4-5]是該領域的熱點問題,但在過程中引入不確定性因素的分析技術尚未成熟,其中:MCS(Monte Carlo Simulation)方法[6]從統計的角度出發,給出了隨機系統一種統計分析方法,但對于大型復雜結構系統,因其工作量繁重而往往不被采用;而從動力學基本原理出發,輔以數學理論方法進行不確定性分析,也可得到較精確結果。梁震濤等[7]利用隨機因子法與代數綜合法計算了板梁組合結構響應的均值、方差表達式,指出隨機性與確定性模型的分析結果確有差異。Adhikari[8]基于隨機矩陣理論提出了量化懸臂板的質量、剛度和阻尼不確定性矩陣變量分布,分析寬頻范圍內系統動態響應。李舜酩等[9]以Lagrange動力學方程和Rayleigh-Ritz能量法為理論基礎,建立了隨機質量板的隨機振動方程,實現振動響應的統計特性分析。王鳳陽等[10]將攝動理論與虛擬激勵法相結合,討論了隨機荷載激勵下不確定參數結構的隨機響應統計特征。此外,還有學者提出了精細積分法[11]及其改進[12],也可得到結構隨機振動響應的概率統計特性。
上述MCS方法及其它結合數學理論改進方法皆是以相關動力學方程為出發點,而本文則從另外一個角度出發求解系統隨機響應,即:只需明確系統各不確定性因素,基于概率統計特性與正交多項式理論逼近隨機響應,并結合FEA計算,利用Fourier-Hermite多項式展開、廣義模型降維和多重Gauss-Hermite數值積分,獲得板結構單點激勵作用下穩態振動響應的顯示多項式函數形式,繼而得出其概率統計特征,并基于此對彈簧支撐離散隨機剛度邊界條件下系統隨機響應開展統計分析,這將對研究板結構等典型系統的隨機動力學響應與傳遞方面具有一定的探索意義。
1 基本原理
對于一個給定的線性多自由度結構系統,其在載荷激勵下的動力學基本方程[13]可表示為

(1)

當系統忽略阻尼或在比例阻尼條件下,質量矩陣M、阻尼矩陣C和剛度矩陣K均為對稱實數矩陣。在模態坐標解耦條件下,應用模態疊加原理,可得單點激勵下原點p處響應為
(2)
式中:Mr、Cr和Kr分別為模態坐標下的模態質量、模態阻尼和模態剛度;φpr和fp(ω)分別為激振點p處第r階模態頻率對應的模態向量和激振力。
考慮系統具有變邊界條件,由于存在系統不確定性,導致上式中模態剛度具有不確定性。此時,系統響應也具有隨機性,可表示為
(3)
式中:x1,x2,…,xN分別為系統變邊界條件下的各個隨機參數變量;顯然,在給定激勵頻率ω下,系統p處原點響應成為隨機參數變量的函數。
然而,僅應用上述動力學理論推導,難以實現對系統響應結果的預測。
2 系統振動響應統計分析
2.1 Fourier-Hermite多項式展開
采用高維模型[14],可將任意一個連續、可微的多變量函數按照各隨機參數進行有限變量的層次函數展開,故式(3)可表示為
(4)
式中:x={x1,x2,…,xN}T∈RN為N維空間隨機參數向量;y0為一個實常數;yi1…iS(xi1,…,xiS)為任意S(S≤N)個隨機參數xi1,…,xiS間耦合作用對多變量響應函數y(x)的貢獻量。
針對式(4),考慮各隨機變量均服從相應的正態分布時,進行Fourier-Hermite多項式展開,得到y(x)的S個變量函數逼近形式,其表達式為[15]

(5)
式中:多項式展開系數

(6)
式中:fk(xk)為單個隨機參數xk的概率密度函數;fX(x)為各隨機參數的聯合概率密度函數;ψj(xi)為以xi為自變量的第j階Hermite多項式函數;m為選取Hermite多項式的最高階數,j≤m。

2.2 廣義模型降維
多維變量函數的廣義降維法由Xu等[16]提出,以結構概率特性分析為出發點,將多變量函數以排列組合的方式展開為
(7)
式中:R為y(x)多項式展開的變量元數,R≤N;y(xk1,xk2,…,xkR-k)中未標明的變量取各自均值。
將式(7)代入式(6)可得多項式展開系數

(8)
以及均值
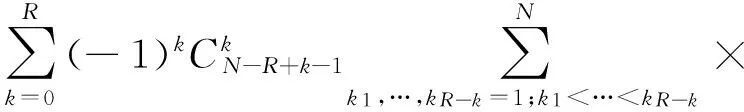
(9)
從式(9)可以看出,引入廣義降維法將N維積分進行積分降維,將大大提高多項式展開系數及均值的計算效率,尤其在S< 針對Hermite多項式的多重Gauss-Hermite求積公式為 (10) 式中:n1,…,nS分別為相應變量xi1,…,xiS所選取積分節點的數目;Wk為各個變量相應積分節點xk處的求積系數。針對含有e-x2特殊項的積分問題,式(10)可將其轉化為累加和的形式,可以更為方便和快捷地求解多項式展開系數與均值。 為提高式(10)的計算精度與效率,可令n=n1=…=nS。 (11) 在簡諧激勵下,矩形板結構在兩側自由、左邊固支-右邊彈簧支撐邊界條件下,受到單點簡諧力激勵起原點振動,其FEM模型如圖1所示。對此,利用文中提出的方法,針對穩態激勵原點處z方向振動位移響應,獲得其系統隨機響應統計特征。 圖1 矩形鋼板簡圖 該鋼板的結構設計參數分布如表1所示。激勵方式為單點正弦載荷激勵,且激振力幅值F=1 000 N,作用于鋼板右上方長、寬各1/3處,即圖1中所示的網格節點上。仿真分析時,為了研究變彈簧支撐邊界條件下鋼板的振動響應特性,假設鋼板右端邊界條件處總剛度均值及其變異系數保持不變且均勻分布于網格節點上;鋼板右端所有支撐彈簧的剛度系數可看作不確定性因素,均服從相互獨立的高斯分布。 表1 結構設計參數分布 對工程結構進行FEM分析時,網格單元尺寸的選取將對結構系統響應求解結果的精確性產生直接影響,因此有必要選取一定的劃分標準。韓增堯[17]最先以波動理論為基礎,提出了針對具體結構的網格單元劃分標準。對于平板,網格單元尺寸要求如下[18] (12) 式中:δ為平板厚度;E為平板材料的彈性模量;μ為泊松比;ρ為質量密度;λ為平板的彎曲波波長;fmax為所考慮的頻率范圍上限。 利用ANSYS有限元軟件對各參數均取其均值的板結構模型進行諧響應分析,可得鋼板在0~100 Hz頻率范圍內激勵點處的z方向位移級譜,如圖2所示。 圖2 激勵點處z方向振動響應的位移級譜 Fig.2 Displacement level spectrum ofzdirection vibration response at the driving point 在第二階固有頻率(22.57 Hz)與第三階固有頻率(32.166 Hz)之間選取25 Hz作為激勵頻率進行后續單頻穩態受迫振動分析。采取1.0×105次直接MCS模擬對上述具有k1~kn隨機剛度系數變量的矩形鋼板結構進行單頻諧響應分析計算,其激勵點處z方向的振動位移響應幅值樣本分布及其概率密度曲線如圖3所示。 以ANSYS軟件作為求解器,根據本文提出的Fourier-Hermite多項式展開式(5)進行振動位移響應分析,其中Gauss-Hermite求積公式選取n=7個積分節點和m=5階Hermite多項式,在此基礎上嵌入1.0×105次局部MCS模擬,分析系統激勵點處z方向的振動位移響應幅值統計特征,其結果如圖4所示,其中包括單變量、雙變量和三變量的z方向位移幅值顯示化多項式函數逼近統計結果。由圖4可知,z方向位移幅值的單變量結果與雙變量、三變量以及直接MCS模擬結果相比具有一定程度偏差,這是由于其忽略了兩個及以上變量之間的耦合作用對響應結果的貢獻,但實際上它們亦對系統位移響應具有一定影響。而采用雙變量與三變量時位移響應的概率密度曲線近似重合,而且能極為準確地反映出直接MCS模擬柱狀圖的分布規律,說明三個以及更多隨機變量間耦合作用對位移響應的貢獻較小。 圖3 激勵點處z方向振動位移響應幅值的樣本分布 表2給出了單點正弦載荷激勵下激勵點處z方向位移響應幅值由式(11)所求得的誤差分析結果,以更為直觀的方式說明了上述分析結果的正確性。工程上對于計算精度一般要求小于等于5%,可知本例中板結構位移響應的單變量、雙變量和三變量逼近均已在誤差允許范圍內,但單變量響應逼近統計結果的各階矩誤差相對于雙變量、三變量來說均較大,可見精確度仍不夠高。盡管雙變量和三變量響應逼近統計結果仍分別具有一定差別,但與單變量和雙變量的差別相比較來看已經很小,說明三個以及更多隨機變量間的耦合作用可以忽略不計。再者,文中僅針對板結構基礎單元,對于實際中復雜結構由于誤差的累積必然導致誤差進一步加大。綜上所述,在計算精準度以及工作量大小的權衡考慮下,雙變量逼近該例中系統響應結果較為合適。 表2激勵點處z方向振動位移幅值的誤差分析 Tab.2Erroranalysisofzdirectionvibrationdisplacementamplitudeatthedrivingpoint% 誤差一階矩二階矩三階矩四階矩單變量0.015850.065440.178640.38416雙變量0.002800.006600.013540.02635三變量0.002330.004240.005910.00756 為了更為準確地獲得變邊界條件下板結構原點響應的統計特征,對平板網格做出如下調整:在長度方向滿足以波動理論為基礎的網格劃分標準下,將網格單元長寬比[19]控制在1.5以內進行網格細化,具體劃分情況如表3所示,其它未標明的結構設計參數由表1提供,且激振點的位置保持不變。以雙變量逼近作為系統振動響應幅值的準確值進行對比分析。 表3 網格劃分詳細信息 圖5給出了在節點彈簧數分別為7、10和13邊界條件下,同一激勵點處z方向的振動位移響應幅值概率統計特征。由該圖可以看出三種邊界條件下位移幅值概率密度曲線的趨勢基本一致,均服從正態分布;但節點彈簧數為7時,由于寬度方向網格劃分與式(12)相悖,導致位移幅值概率密度曲線反映出的均值及分布規律與其它兩種邊界條件相比差異明顯;而節點彈簧數為13時的概率密度曲線與節點彈簧數為10時相比均值幾乎相同,但方差有所減小,說明在板結構右端處于彈性離散邊界條件下及總剛度不變時,隨著離散節點彈簧變量的增加,隨機響應結果的概率統計有向均值處聚攏的趨勢。 為此,在板結構有限元網格滿足劃分標準前提下,進一步對長度和寬度方向網格進行細化,獲得節點彈簧數分別為10,13,16和19邊界條件下系統位移響應幅值概率統計特征,如圖6所示。由該圖可以看出,隨著FEM網格細化,盡管所考慮的節點彈簧變量數逐漸增加,但激勵點處隨機位移響應幅值的均值大致相同,僅方差呈現減小趨勢。可見,考慮板結構右端在隨機離散剛度邊界條件及總剛度一定的情況下,隨著離散節點彈簧變量的增加,隨機響應結果的概率統計有進一步向均值附近聚攏的趨勢;但是這種趨勢在逐漸地減弱,當節點彈簧數量趨近無窮時,即當板右端處于彈性連續邊界條件,隨機響應結果概率統計將滿足某一定分布。 圖5 不同邊界條件下z方向振動位移響應幅值的統計結果 Fig.5 Statistical results ofzdirection vibration response amplitude under different boundary conditions 圖6 不同邊界條件下z方向振動位移響應幅值的變化趨勢 Fig.6 The change trend ofzdirection vibration displacement response amplitude under different boundary conditions 本文結合Fourier-Hermite多項式展開、廣義模型降維法以及Gauss-Hermite數值積分,提出了一種關于結構系統隨機響應統計特征的分析方法,并結合網格劃分技術對系統響應的預測結果進一步對比分析。主要結論如下: (1)隨著考慮系統隨機變量元數的增加,其系統穩態位移幅值響應統計特征將更加符合直接MCS模擬求解結果,但調用有限元次數與計算成本也將隨之呈多項式增長,故應當根據誤差分析選擇適當隨機變量元數,以在滿足精度前提下盡可能減少計算工作量。 (2)當考慮隨機參數變量個數較多時,采用文中方法仍可獲得較高的計算效率和求解精度。 (3)本文并未假定系統穩態位移響應服從某一特定分布,故該方法適用性強。 (4)對網格逐步細化及離散節點彈簧數漸增的分析結果表明,FEM隨機響應統計分布將向均值附近聚攏,且趨于連續隨機剛度邊界條件的某一確定分布。 然而,目前存在的不足之處是,當板結構右端處于彈性連續隨機剛度邊界條件時,建模以及響應逼近求解過程的工作量均將大大增加,需借助理論分析來進一步完善;再者,文中僅針對單點單頻激勵下板結構原點穩態振動隨機響應的分析,對于跨點響應分析亦需進一步拓展研究。 參 考 文 獻 [1] ADHIKARI S, FRISWELL M. Random eigenvalue problems in structural dynamics[J]. International Journal for Numerical Methods in Engineering, 2004, 69(3): 562-591. [2] 高偉,陳建軍,馬娟,等. 平穩隨機激勵下線性隨機桁架結構動力響應分析[J]. 振動工程學報,2004,17(1):44-48. GAO Wei, CHEN Jianjun, MA Juan, et al. Dynamic response analysis of linear stochastic truss structures under stationary random excitation[J]. Journal of Vibration Engineering, 2004, 17(1): 44-48. [3] 高超,李亞軒,肖斌,等. 考慮參數不確定的系統固有頻率統計分析[J]. 現代振動與噪聲技術,2017(12):609-616. GAO Chao, LI Yaxuan, XIAO Bin, et al. Statistical analysis of natural frequency of the system with parameter uncertainties[J]. Modern Vibration and Noise Technology, 2017(12):609-616. [4] 蒲育,滕兆春,趙海英. 四邊彈性約束矩形板面內自由振動的DQM求解[J]. 振動與沖擊,2016,35(12):55-60. PU Yu, TENG Zhaochun, ZHAO Haiying. In-plane free vibration analysis for rectangular plates with elastically restrained edges by differential quadrature method[J]. Journal of Vibration and Shock, 2016, 35(12): 55-60. [5] 剛憲約,李麗君,柴山,等. 求解運動激勵結構動態響應的固定邊界-模態疊加法[J]. 機械工程學報,2016,52(13):87-93. GANG Xianyue, LI Lijun, CHAI Shan, et al. Fixed boundary mode superposition method for the dynamic analysis of base motion excited structures[J]. Chinese Journal of Mechanical Engineering, 2016, 52(13): 87-93. [6] HURTADO J E, BARBAT A H. Monte Carlo techniques in computational stochastic mechanics[J]. Archives of Computational Methods in Engineering, 1998, 5(1): 3-29. [7] 梁震濤,陳建軍,馬洪波. 隨機參數板梁組合結構有限元分析的隨機因子法[J]. 西安電子科技大學學報,2005,32(2):201-205. LIANG Zhentao, CHEN Jianjun, MA Hongbo. Random factor method of finite element analysis for random plate-beam composite structures[J]. Journal of Xidian University, 2005, 32(2): 201-205. [8] ADHIKARI S. Matrix variate distributions for probabilistic structural dynamics[J]. AIAA Journal, 2007, 45(7): 1748-1762. [9] 李舜酩,廖慶斌,尚偉燕. 隨機質量板的振動響應及其統計分析[J]. 振動工程學報,2009,22(1):60-64. LI Shunming, LIAO Qingbin, SHANG Weiyan. Analyses of vibration responses and its statistical characteristics for random mass plate[J]. Journal of Vibration Engineering, 2009, 22(1): 60-64. [10] 王鳳陽,趙巖,林家浩. 參數不確定結構平穩隨機響應虛擬激勵攝動方法[J]. 大連理工大學學報,2011,51(3):320-325. WANG Fengyang, ZHAO Yan, LIN Jiahao. Pseudo-excitation perturbation method for stationary random response of structure with uncertain parameters[J]. Journal of Dalian University of Technology, 2011, 51(3): 320-325. [11] 張森文,曹開彬. 隨機振動響應計算的精細積分時域平均法[J]. 振動工程學報,1999,12(3):367-373. ZHANG Senwen, CAO Kaibin. Time-domain averaging of precise integration method for response of random vibration[J]. Journal of Vibration Engineering, 1999,12(3): 367-373. [12] 宋向華,安偉光,蔣運華. 任意隨機激勵下結構隨機振動分析的一種數值方法[J]. 振動與沖擊,2013,32(13):147-152. SONG Xianghua, AN Weiguang, JINAG Yunhua. A numerical method for random vibration analysis of structures under arbitrary random excitations[J]. Journal of Vibration and Shock, 2013, 32(13): 147-152. [13] 傅志方. 振動模態分析與參數辨識[M]. 北京:機械工業出版社,1990. [14] RABITZ H, ALI? F. General foundations of high-dimensional model representations[J]. Journal of Mathematical Chemistry, 1999, 25(2/3): 197-233. [15] RAHMAN S. A polynomial dimensional decomposition for stochastic computing[J]. International Journal for Numerical Methods in Engineering, 2008, 76(13): 2091-2116. [16] XU H, RAHMAN S. A generalized dimension-reduction method for multidimensional integration in stochastic mechanics[J]. International Journal for Numerical Methods in Engineering, 2004, 61(12): 1992-2019. [17] 韓增堯. 復雜航天器聲振力學環境預示技術研究[D]. 北京:中國空間技術研究院,2000. [18] 徐孝誠,尹立中. 關于結構高頻響應分析中有限元網格劃分的細化標準[J]. 振動與沖擊,2002,21(1):52-53. XU Xiaocheng, YIN Lizhong. On fining standard of fem meshing used in high frequency structure response analysis[J]. Journal of Vibration and Shock, 2002, 21(1): 52-53. [19] 漆文邦,鄭超. 基于單元不同長寬比網格劃分的有限元誤差分析研究[J]. 中國農村水利水電,2010(2):108-110. QI Wenbang, ZHENG Chao. A study of sensitivity to mesh distortion of isoparameter elements[J]. China Rural Water and Hydropower, 2010(2): 108-110.2.3 多重Gauss-Hermite積分
2.4 誤差分析

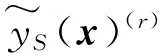
3 數值仿真
3.1 模型建立


3.2 網格單元劃分

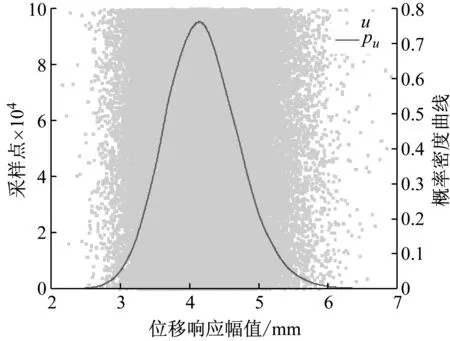
3.3 位移響應預測分析


3.4 變彈性隨機邊界條件的影響



4 結 論

