基于t分布混合模型的半監督網絡流分類方法

董育寧，朱善勝，趙家杰

DONG Yuning,ZHU Shansheng,ZHAO Jiajie

南京郵電大學 通信與信息工程學院，南京 210003

1 引言

近年來，由于網絡多媒體業務的不斷發展，網絡流量的監測管理和網絡安全的難度也隨之提升。根據Cisco的預測報告[1]，到2021年，全球每年的IP網絡流量將達到3.3 ZB（ZB；1 000 Exabytes[EB]），將比2016年提高3.2倍；其中視頻流量將占所有消費流量的82%。因此，對網絡的流量進行分類管理在改善網絡環境、保障網絡安全等方面具有重要的意義。

網絡流分類主要分為四種形式[2]：基于端口、深度包檢測、基于統計行為和基于機器學習的方法。然而，由于新型網絡應用層出不窮，加密傳輸、動態端口號等技術的出現使得前兩種方法對流分類的準確率大為降低。目前通常采用機器學習的方式進行流分類。

基于機器學習的流分類算法可以分為有監督分類[3]、無監督分類（聚類）[4]和半監督分類[5]。半監督分類是有監督分類和無監督分類的結合。由于其結合了已知標簽的樣本，可以提前獲取部分信息，所以被一些算法所采用。Jun Zhang[6]等人提出了一個半監督的分類模型。該方法使用K-Means和Random Forest算法構建分類模型，并采用流袋進行優化。實驗表明該模型可以較好地提高對短時未知應用（zero-day applications）的流分類準確率。Yu Wang[7]等人在考慮了背景信息的情況下，將馬氏距離應用于K-Means方法中，提高了分類的準確度。此外，他們將該算法加入對未知聚類的分析，并應用于未知協議的流分類[8]。Shukla[9]等人使用KMedoids方法對KDD CUP 99數據庫進行半監督分類的研究。李林林[10]等人針對網絡流量分類的類不均衡問題，提出一種K-Means和kNN（k-Nearest Neighbor）相結合的半監督流量分類算法，提高了非均衡流中特別對小類流的識別率。

對于高斯混合模型（Gaussian Mixture Model，GMM）和期望最大化（Expectation Maximization，EM）算法，國內外相關學者也進行了相當多的研究。程華[11]等人根據網絡流尺度的Log-normal分布，對數據集進行了GMM建模。Songyin Liu[12]等人將EM算法結合了q-DAEM，降低了傳統EM算法的迭代次數。然而，以上EM算法均是基于GMM的。而高斯分布本身對于樣本尾部的擬合效果較差，易受到噪聲的影響。本文在EM算法基礎上，結合t分布混合模型（Student’s t-distribution Mixture Model，TMM）進行改進，并用半監督分類方法驗證了算法的有效性。

本文的貢獻主要包括以下兩點。第一，現有文獻中的無監督和半監督的流分類方法通常采用K-Means、EM等算法。但是采用這些算法擬合的模型對數據樣本邊緣及離群樣本比較敏感。因此，本文在流分類時采用t分布代替傳統的高斯分布，結合t分布混合模型（TMM）對網絡多媒體業務流進行擬合，從而提高了分類的準確率。第二，傳統的EM算法執行效率比較低，這是因為如果數據集本身比較復雜，數據樣本的邊緣信息有可能對每次迭代產生影響，所以收斂速度較慢。本文采用更加復雜的TMM，執行效率將更加低下。為了提高EM的收斂速度，本文使用3σ準則對TMM模型進行限制，提出了有限t分布混合模型（Limited t-distribution Mixture Model，LTMM），降低了EM算法的迭代次數。理論分析和實驗結果表明，本文提出的算法模型優于現有文獻中的K-Means和高斯混合模型的EM算法。

2 t分布混合模型流分類算法

2.1 高斯混合模型和EM算法

高斯分布（Gaussian distribution）可以較好地描述一般數據樣本的分布情況。對于數據集x={x1,x2,…,xN}T，多維高斯分布可由公式（1）表示：

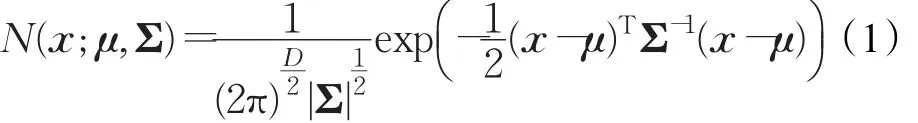
其中，μ表示數據集x的均值；Σ表示數據集x的協方差矩陣；D表示高斯分布的維度。對于網絡流分布的數據集而言，每個數據流樣本可以通過多種QoS（Quality of Service）特征表示，且每個特征之間還存在一定的相關性。所以為了描述多媒體業務數據集的分布情況，可以引入高斯混合模型（GMM）對樣本進行擬合[13]，即K個高斯分布的期望：

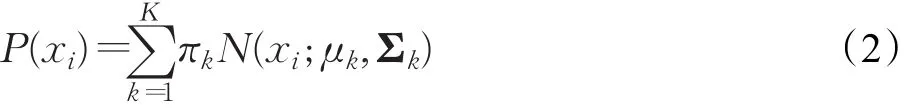
其中，表示第k個高斯分布，該高斯分布的系數用πk表示。需要注意的是，πk應滿足公式（3）。

GMM的估計通常采用期望最大化算法（Expectation Maximization，EM）進行迭代擬合。公式（4）～（7）給出了EM算法的迭代公式[7]：

E步：

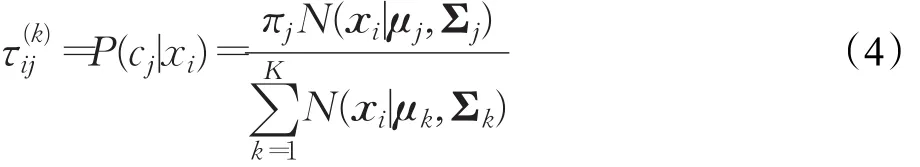
M步：

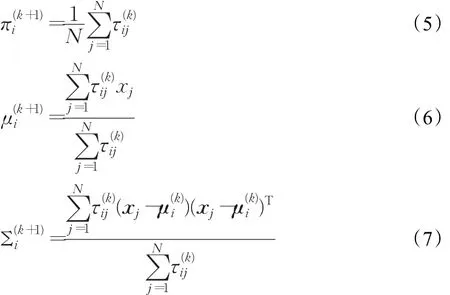
EM算法的收斂條件，即似然函數（公式（8））的變化量小于誤差值eps，則表示迭代結束。

2.2 t分布混合模型和EM算法

上文提到，高斯分布容易受到噪聲值的干擾，對數據樣本邊緣的擬合較差。為了能夠更好地擬合數據樣本尾部的取值，本文引入了學生t分布（Student’s tdistribution，以下簡稱為t分布）來代替原有的高斯分布。標準的一維t分布由公式（9）所示：

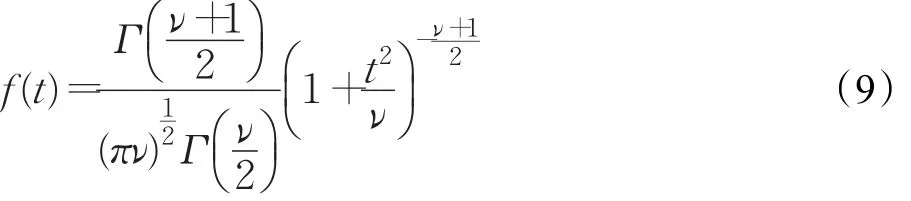
其中，Γ(·)為Gamma函數，ν代表自由度。當ν=1時，t分布退化為柯西分布（Cauchy distribution）；當ν=∞時，t分布退化為高斯分布。因此，t分布可以看作高斯分布的拓展。

圖1的直方圖反映了HTTP網頁瀏覽的平均數據包大小的分布情況。分別用高斯分布和t分布進行擬合。由于使用t分布所具有的“長尾”特性能夠更好地匹配數據樣本尾部的分布，因此使用t分布模型對數據樣本進行擬合，所得到的結果將更準確。

圖1 HTTP網頁瀏覽數據包大小的擬合曲線

從物理角度而言，每種多媒體業務流樣本的分布是隨機且獨立的。根據中心極限定理，每種業務可以用高斯分布擬合，而多個業務顯然可以構成高斯混合。t分布作為高斯分布的拓展，因此多媒體業務流的數據集使用GMM拓展的t分布混合模型（Student’s t-distribution Mixture Model，TMM）來描述也是相對合理的。常規的多維t分布公式可由式（10）和式（11）給出，TMM的公式可由式（12）表示。

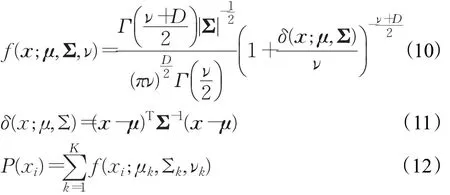
TMM也可以使用EM算法進行擬合。由于TMM還受到自由度ν的影響，根據文獻[14]，t分布混合模型的EM算法可以修正為：

E步：

M步：似然函數：

需要注意的是，算法中自由度ν是維度為聚類數K的向量，完整的EM迭代需要不斷更新ν的值。為了簡化EM算法的計算量，本文取ν為常數，并在實驗中用多個ν的取值進行了驗證。綜上所述，t分布混合模型的EM算法如下所示：

TMM(x1,x2,…,xN,K)

begin

初始化K個中心，記為 μ1,μ2,…,μK

初始化混合模型參數π1,π2,…,πK←1/K

計算每個混合模型協方差Σ1,Σ2,…,ΣK

while true

E步，公式（13）～（14）

M步，公式（15）～（17）

計算似然函數L(x)，公式（18）

if|L(k+1)(x)-L(k)(x)|＜eps//收斂條件

break

end if

end while

end

3 有限t分布混合模型

3.1 t分布和3σ準則

高斯分布存在3σ準則，即數據樣本 X出現在(μ-3σ,μ+3σ)外的取值不足0.3%。換句話說，數據樣本在雙側置信度為99.73%的置信區間是(μ-3σ,μ+3σ)。用數學語言可描述為：

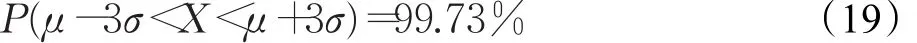
在本文的流分類數據集中，可以用到該結論。我們認為超過這一區間的樣本幾乎不可能發生，即視為離群樣本。為了避免這些離群樣本對模型的擬合帶來錯誤的影響，因此可以事先忽略這些離群樣本，從而加快算法的收斂。

因為t分布可以看成高斯分布的拓展，所以t分布模型的優化和高斯模型類似。但是由于自由度ν的存在，此時3σ準則已不完全適用于99.73%的置信區間。通過查詢t分布表，得到了一個修正的t分布置信區間，如表1所示。

3.2 有限t分布混合模型

傳統的EM算法在每一次迭代的時候都要通過第k

步的 μ(k)和 Σ(k)值來更新第k+1步的 μ(k+1)和 Σ(k+1)值。在引入t分布混合模型后，由于模型更加復雜，可能導致計算量上升，迭代次數增加。為了減少迭代次數，本節結合修正的3σ準則，對EM算法的每一次迭代進行了優化，并提出了有限t分布混合模型（Limited t-distributionMixture Model，LTMM）。

表1 修正的t分布置信區間

根據1.1節，計算高斯混合模型的E步時，需要計算馬氏距離的平方(x-μ)TΣ-1(x-μ)。由于馬氏距離可以看成是歐式距離‖‖x-μ的拓展[7]，所以可以在計算馬氏距離時加上限制。這里以ν=5為例，限制條件如公式（20）所示：

如果某個樣本到所有K個t分布的馬氏距離均大于5.507 0，那么該樣本可以看作是離群樣本（outlier）。每一次計算M步的時候，首先忽略掉這些離群樣本，那么計算得到μ和Σ就不會受到這些樣本的影響。在這一輪迭代結束后，需要把忽略的樣本重新加回，保證離群樣本不被錯誤劃定。這樣就完成了TMM模型的優化。把這種改進的模型稱為有限t分布混合模型（LTMM）。同理，高斯混合模型可優化為有限高斯混合模型（LGMM）。

綜上所述，有限的t分布混合模型的EM算法如下所示：

LTMM(x1,x2,…,xN,K)

begin

初始化K個中心，記為μ1,μ2,…,μK

初始化混合模型參數π1,π2,…,πK←1/K

計算每個混合模型協方差Σ1,Σ2,…,ΣK

while true

E步，公式（13）～（14），計算離群點，公式（21）

排除離群點，執行M步，公式（15）～（17）

計算似然函數L(x)，公式（18）

if|L(k+1)(x)-L(k)(x)|＜eps//收斂條件

break

end if

end while

end

3.3 有限t分布混合模型分析

為了更直觀地說明迭代過程，這里構建了一個簡化的數據分布。圖2生成了3個二維高斯分布，其均值和協方差矩陣分別為布均有50個點。那么它們的迭代過程如圖2所示。

圖2中有限t分布模型中的⊙代表迭代考慮的離群樣本。原始數據分布中，存在兩個距離數據分布較遠的離群樣本。迭代結束后，結合TMM的EM算法一共迭代了19次，而LTMM僅迭代了5次。從圖2可以看出，雖然開始時迭代效果接近，但當TMM迭代6次之后，其聚類中心的更新都極其微小；而LTMM不受離群樣本的干擾，收斂速度很快。這是由于LTMM在每次迭代時能找到更接近迭代中心的μ和Σ值，所以降低了迭代次數，加快了算法的收斂。

4 實驗分析

4.1 實驗模型建立

本節給出了流分類的實驗模型，如圖3所示。實驗模型可以分為3個部分：數據預處理、聚類過程和分類過程。預處理部分包括：對網絡多媒體流進行z-score標準化（即使用標準分數使數據無量綱化[15]）、特征選擇、劃分已標識/未標識樣本；聚類過程采用KMeans、SBCK[8]、K-Medoids[9]以及各個混合模型（GMM、TMM、LTMM）進行對比。得到聚類結果可分為三種情況：聚類中沒有已標識的樣本，則該聚類可視為未知聚類，不在本文考慮范圍內；聚類中已標識樣本的類型僅有一種，則該聚類中所有的樣本均可劃分為該類型；第三種是聚類含多種已標識樣本的類型。對于這類混合簇，可以進一步對簇中未知樣本進行細分類判定，提高分類的準確度[10]。部分文獻[6]采用“多數投票”的方式，少部分文獻[8，10]進行了細分類工作。由于Random Forest算法不僅分類速度快、分類準確率高，而且相比其他算法可以減少過擬合的情況，所以本文將采用Random Forest作為細分類工作。最后將三種聚類情況綜合即可得到半監督流分類模型的分類的準確率。

本文采用半監督方法分類，因而隨機選取數據集中的10%作為已標識的樣本，剩余的90%作為未標識的樣本。為了提高結果的準確性和可靠性，對每個實驗均進行10次重復驗證取平均值。

4.2 數據集和評價指標

本文數據集采用南京郵電大學校園網內抓取的網絡多媒體業務流。數據集的時間跨度是2014年4月到2015年8月，使用的抓包工具是WireShark1http：//wiki.wireshark.org/。本文涉及的網絡多媒體業務主要可以分為6類，如表2所示。每類業務均為60條數據流，每條數據流的長度均為30分鐘。分別選用典型的應用進行實驗。

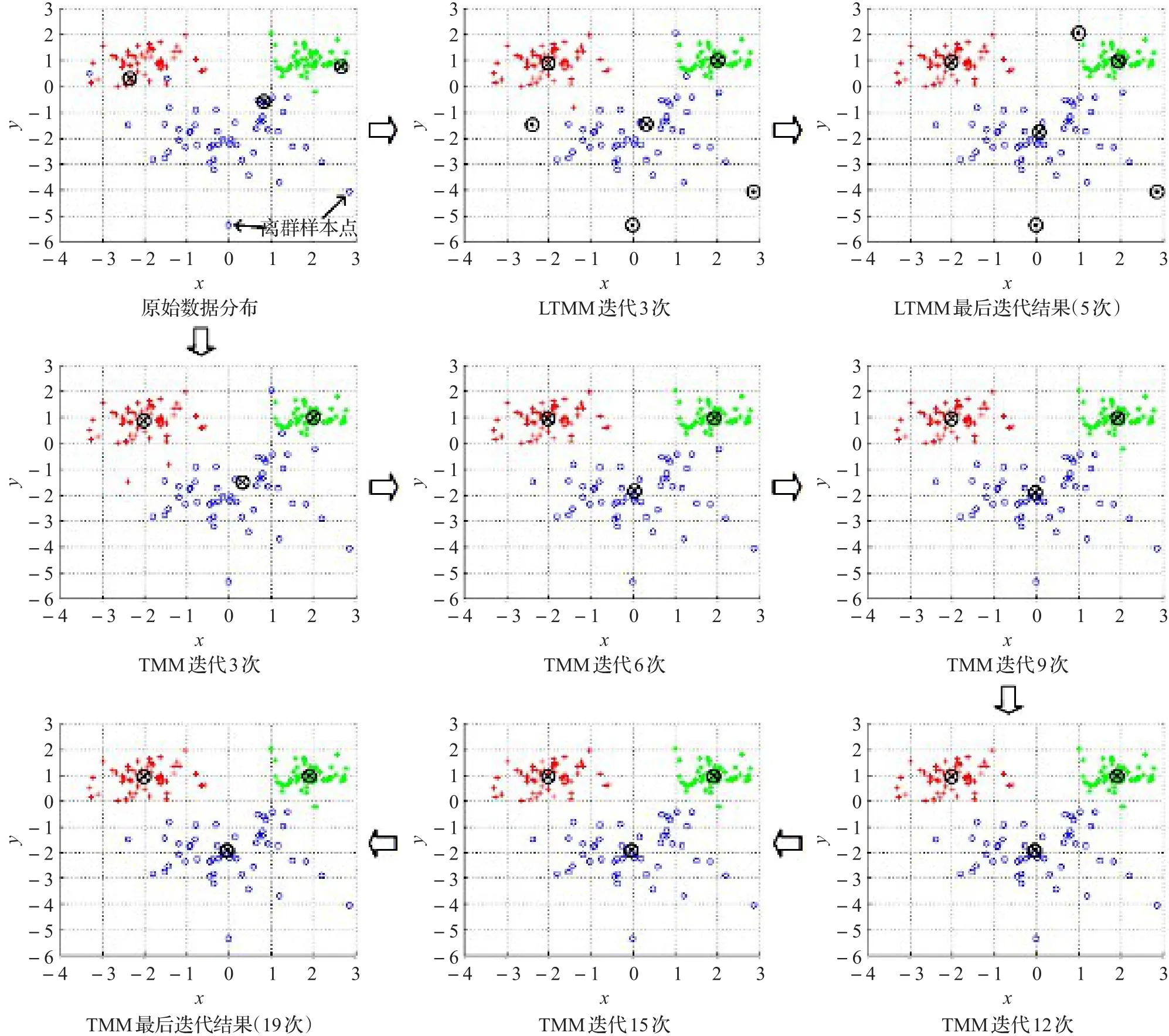
圖2 傳統t分布模型和有限t分布模型的迭代對比

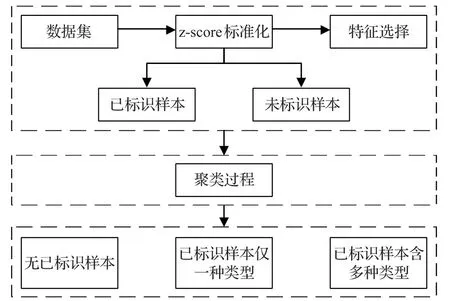
圖3 多媒體業務的半監督流分類模型

表2 多媒體業務流數據集

衡量網絡流的分類結果通常引入四個評價指標：查準率（Precision）、查全率（Recall）、F-測度（F-measure）和總體正確率（Accuracy）。在引入四個指標之前，需要給出二分問題的幾種分類結果，如表3所示。

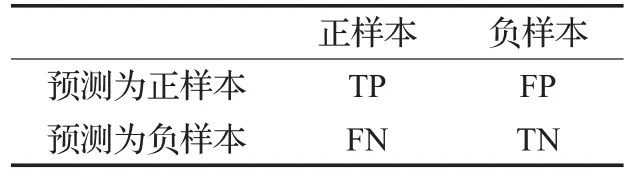
表3 二分類問題的分類結果

其中，TP（True Positive）表示正確樣本預測為正確分類的數目；FP（False Positive）表示錯誤樣本被預測為正確分類的數目；FN（False Negative）表示正確樣本被預測為錯誤分類的數目；TN（True Negative）表示錯誤樣本預測為錯誤分類的數目。進而，四種指標分別由公式（21）～（24）表示：

4.3 特征選擇

常用的網絡多媒體業務流的QoS統計特征包括數據包大小、數據包傳輸間隔等。根據數據流傳輸方向，QoS特征可以分為上行、下行以及整體方向。由于本文針對的網絡多媒體流主要集中于下行業務，即下行方向的數據流可以承載更多的特征信息，因此本文主要對下行方向數據流的QoS統計特征進行了相應的研究。

為了能夠更加有效地進行流分類，需要找到一個簡潔有效的特征組合，以提高分類的準確率，同時降低分類的復雜度。然而，并沒有一種最優的特征選擇算法能夠完全適用于所有數據樣本的分類[16]。因此，本文選用了6種常用的特征選擇算法，并在本文數據集的基礎上進行了特征選擇。本文采用信息增益（InfoGain）、信息增益率（GainRatio）或卡方檢驗（Chi-square）這三種方法選出的特征進行進一步的研究。這些QoS分類特征由表4列出。

表4 實驗所采用的特征

不同特征選擇算法的總體正確率由圖4所示。從圖4可以看出，InfoGain、GainRatio和Chi-square這三種方法選出的特征一致，得到的分類正確率較高。此外，雖然一致性特征選擇方法（Consistency）對K-Means算法可以獲得較高的總體正確率，但在TMM和LTMM算法的總體正確率卻不如InfoGain等三種方法選出的特征。

圖4 QoS特征選擇算法的總體正確率

4.4 自由度的確定

根據3.2節，t分布混合模型根據自由度ν的不同，最后得出的擬合模型也隨之不同。因此，為了找到一個比較合適的自由度ν以擬合最后的數據樣本，需要對自由度ν進行確定。本節將對提出的TMM和LTMM算法的自由度進行分析。

圖5對本文數據集分別執行TMM和LTMM算法，聚類數K取15。從圖中可以得出，當ν=3或ν=5的時候，兩種模型得到的總體正確率比較高，即更加貼近實際的數據樣本。在接下來的實驗中，主要采用這兩種自由度進行分析。

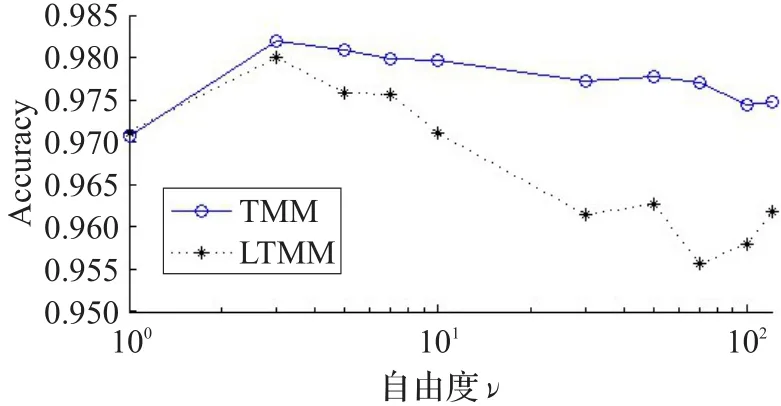
圖5 TMM和LTMM算法的自由度分析

4.5 聚類數的影響

不同的聚類數對K-Means、EM算法均有較大的影響。本節使用半監督流分類模型，探討不同聚類算法在不同聚類數條件下的影響。

圖6給出了不同的聚類數對不同算法的總體正確率。從圖6（a）中可以看出，EM算法（GMM和TMM）要優于K-Means部分的算法（K-Means、SBCK和KMedoids）。這是由于K-Means部分的算法通常采用歐氏距離，獲得的簇的形狀往往是球形的，對非球形簇的聚類并不準確[11]。雖然文[7]中的實驗提到他們的算法SBCK要優于GMM，但可能是由于數據集之間的差異，導致本文實驗中對SBCK算法的總體正確率較低。對于GMM和TMM而言，本文采用的模型無論取自由度ν=3或5，總體分類正確率均高于GMM模型的分類正確率。因而采用TMM能夠更精確地擬合多媒體業務流的數據集。

圖6（b）驗證了常規混合模型（GMM、TMM）和改進的混合模型（LGMM、LTMM）之間的差異。從圖中可以看出，TMM模型的分類正確率均要高于GMM模型的分類正確率，而改進混合模型可能會導致總體分類正確率的降低。這是由于改進混合模型LTMM采用了3σ準則，在每次聚類時可能會過度忽略模型邊緣點的影響，因而造成在某些聚類數下的分類正確率的降低。但TMM模型和LTMM模型的擬合結果均優于GMM模型，證明LTMM模型在分類正確率方面還是可以接受的。

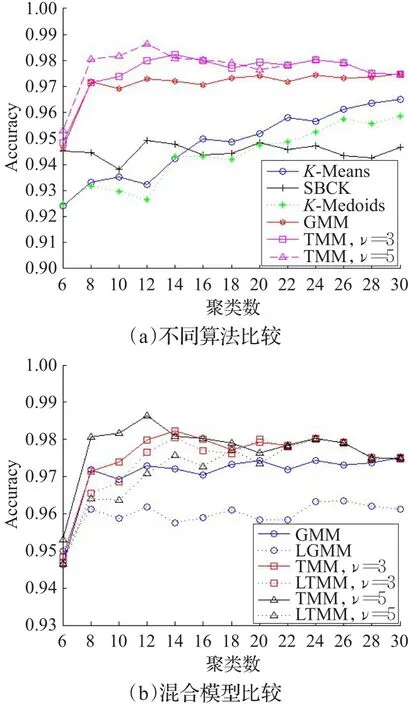
圖6 不同聚類數的影響

為了更明顯地看出每一類的分類情況，圖7列出了各個算法在聚類數為15時的F-measure值。可以看出，本文使用的TMM和LTMM算法確實要優于其他列出的算法。

4.6 迭代次數比對

在本節中，主要對混合模型算法的迭代次數進行實驗比較，以驗證2.3節的理論分析結果。為簡單起見，取聚類數為15，并重復做10次實驗取平均值。各算法迭代次數的平均值如表5所示。

從表5中可以得出，使用TMM擬合后，由于算法復雜度增加，因此迭代次數比GMM有所增加。但是有限t分布混合模型（LTMM）的迭代次數小于t分布混合模型（TMM），證明了LTMM可以顯著降低算法的迭代次數。雖然LTMM的分類正確率相比TMM有略微的下降，但是由于在迭代次數上降低較明顯，所以有限t分布混合模型是可以接受的。

圖7 不同算法的F-measure比較

表5 不同算法迭代次數比對

4.7 TMM、LTMM特點及適應場景

由實驗可知，TMM、LTMM相較于K-Means和GMM，在準確率、F測度和總體正確率的指標都更優。對t分布自由度v的值進行適當的調整，能夠更好地匹配數據樣本的尾部分布，提高抗噪聲性能，因此t分布擬合的模型可以更好地適用于尾部較長情形。由于引入EM算法，TMM、LTMM擁有EM的優點，能夠穩定地處理數據集中的缺損、截尾等不完全數據，但此模型的運算復雜度較高，比較適用于較小型的數據集。從表5可知，與TMM相比，LTMM精確度稍有下降，但高于GMM；然而，其計算復雜度比TMM降低近一半，與GMM相當，所以適用于對計算時間要求較為苛刻的場景。

5 結束語

本文結合t分布混合模型對多媒體業務流進行分類，并用理論和實驗證實了t分布混合模型的有效性。相比于高斯混合模型，t分布混合模型對數據集邊緣樣本的擬合更加精確。為了減少模型中EM算法的迭代次數，本文對t分布模型加以改進，并提出了有限的t分布混合模型，顯著地降低了迭代次數。然而，該算法在處理過大的數據集時，可能會導致執行效率低下的問題。在未來的工作中，將進一步優化本文算法，以適用于較大數據集和高維特征的情況。

：

[1]White paper：Cisco VNI forecast and methodology[EB/OL].[2016-2021].http：//www.cisco.com/c/en/us/solutions/collateral/service-provider/ip-ngn-ip-next-generation-network/white_paper_c11-481360.html.

[2]Al Khater N，Overill R E.Network traffic classification techniques and challenges[C]//Tenth International Conference on Digital Information Management.IEEE，2015：43-48.[3]Hardt M，Price E，Srebro N.Equality of opportunity in supervised learning[C]//Advances in neural information processing systems，2016：3315-3323.

[4]Li Y，Paluri M，Rehg J M，et al.Unsupervised learning of edges[C]//Computer Vision and Pattern Recognition.IEEE，2016：1619-1627.

[5]Chapelle O，Sch?lkopf B，Zien A.Semi-supervised learning[C]//Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining.[S.l.]：Springer-Verlag，2009：588-595.

[6]Zhang J，Chen X，Xiang Y，et al.Robust network traffic classification[J].IEEE/ACM Transactions on Networking，2015，23（4）：1257-1270.

[7]Wang Y，Xiang Y，Zhang J，et al.Internet traffic classification using constrained clustering[J].IEEE Transactions on Parallel&Distributed Systems，2014，25（11）：2932-2943.[8]Wang Y，Chen C，Xiang Y.Unknown pattern extraction forstatisticalnetwork protocolidentification[C]//Local Computer Networks.IEEE，2015：506-509.

[9]Shukla D B，Chandel G S.An approach for classification of network traffic on semi-supervised data using clustering techniques[C]//Nirma University International Conference on Engineering，2013：1-6.

[10]李林林，張效義，張霞，等.基于K均值和k近鄰的半監督流量分類算法[J].信息工程大學學報，2015，16（2）：234-239.[11]程華，房一泉.基于聚類分析的網絡流量高斯混合模型[J].華東理工大學學報：自然科學版，2010，36（2）：255-260.

[12]Liu S，Hu J，Hao S，et al.Improved EM method for internet traffic classification[C]//2016 8th International Conference on Knowledge and Smart Technology（KST），Chiangmai，2016：13-17.

[13]Dukkipati A，Ghoshdastidar D，Krishnan J.Mixture modeling with compact support distributions for unsupervised learning[C]//2016 International Joint Conference on Neural Networks（IJCNN），Vancouver，BC，2016：2706-2713.[14]Yao W，Wei Y，Yu C.Robust mixture regression using the t-distribution[J].Computational Statistics&Data Analysis，2014，71（3）：116-127.

[15]Han J，Pei J，Kamber M.Data mining：concepts and techniques[M].3rded.SanFrancisco：MorganKaufmann Publishers，2011.

[16]Fahad A，Tari Z，Khalil I，et al.Toward an efficient and scalable feature selection approach for internet traffic classification[J].Computer Networks，2013，57（9）：2040-2057.