基于貝葉斯非局部平均濾波的超聲圖像斑點噪聲抑制算法

方宏道，周穎玥，林茂松

(1.西南科技大學(xué) 信息工程學(xué)院，四川 綿陽 621010； 2.特殊環(huán)境機器人技術(shù)四川省重點實驗室(西南科技大學(xué))，四川 綿陽 621010)

0 引言

超聲成像是觀察人體內(nèi)部組織器官(例如腹部、乳房、肝臟、腎臟和肌肉骨骼)的強大技術(shù)。與其他醫(yī)學(xué)診斷方法相比，超聲成像具有對人體無害、非放射性、低成本、高效等優(yōu)點[1]；因此，超聲成像技術(shù)在臨床應(yīng)用上顯得更加重要，特別表現(xiàn)在觀察孕婦胎兒生長狀況和診斷腹部器官損傷這些方面。然而，像所有相干成像方法一樣，超聲圖像容易被斑點噪聲[2]污染。斑點噪聲是一種粒狀圖案，由隨機分布的結(jié)構(gòu)散射的能量干擾所引起的，其分辨率超過圖像系統(tǒng)的能力。由于這種斑點噪聲的過多存在，大大降低了超聲圖像的質(zhì)量，嚴重影響了醫(yī)生對病人的疾病作出正確的判斷，因此，有必要研究如何去除超聲圖像中的斑點噪聲。

近些年來，許多去除斑點噪聲的方法已經(jīng)被廣泛研究。這些方法可以簡單地分為三類，即局部自適應(yīng)濾波、基于偏微分方程濾波和小波濾波。常用的自適應(yīng)濾波，例如Lee濾波[3]、Kuan濾波[4]、Fronst濾波[5]、中值濾波器[6-7]等，這些方法都是將斑點噪聲當作乘性噪聲對待的。在20世紀90年代初，Lopes等[8]建議通過對像素進行分類來改進Lee濾波和Frost濾波，以便于對不同的類采用特定的處理。基于這一思想，自適應(yīng)斑點減少(Adaptive Speckle Reduction, ASR)濾波器[9]就是利用局部圖像統(tǒng)計來確定特定區(qū)域被進一步處理。雖然局部自適應(yīng)濾波器具有較低的算法復(fù)雜度，但它們往往會使圖像模糊，并且不能得到滿意的去噪結(jié)果。基于偏微分方程的方法有各向異性擴散(Anisotropic Diffusion, AD)濾波[10-11]和全變分最小模型(Total Variation, TV)[12]，這些方法都可以用來進行超聲圖像去噪處理。改進的各向異性擴散(Speckle Reducing Anisotropic Diffusion, SRAD)[13-14]是一個非線性迭代濾波器，推導(dǎo)出瞬時方差系數(shù)作為邊緣檢測器。與前面方法相比，基于偏微分方程的方法在保護圖像邊緣的同時，對圖像進行了平滑處理。然而，有意義的結(jié)構(gòu)細節(jié)在迭代的過程中不幸被去除。一些基于小波的方法[15]開始用于斑點減少的研究，基于這一假設(shè)，斑點噪聲可以用對數(shù)運算轉(zhuǎn)換為加性高斯噪聲。然而，作為非線性運算，對數(shù)變換不僅完全改變了斑點的統(tǒng)計，而且偏離了噪聲的平均值。為了放寬這種限制性假設(shè)，首先利用小波系數(shù)構(gòu)建基本邊緣圖，然后使用前向和后向擴散技術(shù)進行圖像去噪[16]。Achim等[17]利用貝葉斯框架來確定適應(yīng)于非高斯信號的統(tǒng)計的小波閾值。Khare等[18]提出使用復(fù)尺度小波系數(shù)的虛分量來檢測強邊，然后在非邊緣點處對小波系數(shù)的幅度進行收縮。另外，基于稀疏表示的圖像去噪技術(shù)在圖像高斯噪聲的去除中表現(xiàn)很好[19]，根據(jù)噪聲圖像所訓(xùn)練出的自適應(yīng)過完備字典能更加稀疏地表示圖像塊信號，使得去噪效果進一步提升。隨著深度學(xué)習(xí)技術(shù)在信號處理領(lǐng)域的廣泛應(yīng)用，一些學(xué)者嘗試利用神經(jīng)網(wǎng)絡(luò)、深度學(xué)習(xí)的方法來去除圖像中的高斯噪聲[20]，也取得了非常不錯的效果。

非局部平均(Non-Local Means, NLM)濾波算法[21-23]是一種簡單有效的算法。該算法充分考慮了圖像中充滿著豐富的冗余信息，采用非局部加權(quán)平均的方式對圖像去噪，在加性高斯噪聲的去除上取得了超越傳統(tǒng)算法的結(jié)果。為了將該算法應(yīng)用于非高斯的噪聲模型，有研究提出了一種貝葉斯非局部平均濾波器[24]，極大地擴展了原算法在其他噪聲模型上的應(yīng)用。本文以被斑點噪聲污染的超聲圖像為研究對象，結(jié)合斑點噪聲的模型，利用貝葉斯公式推導(dǎo)出兩種新的統(tǒng)計距離來比較圖像塊的相似性，并用于非局部平均濾波器中，提高了算法對于噪聲模型的魯棒性。為了降低算法的復(fù)雜度，本文采用了塊預(yù)選擇的方法來選擇最相關(guān)的圖像塊，從而避免無用權(quán)重的計算，在一定程度上提升了去噪效果，并且加速了算法。另外，在參數(shù)的設(shè)置上，本文根據(jù)多次實驗總結(jié)出一種定量估算濾波參數(shù)h最優(yōu)值的方法。在算法實現(xiàn)方面，本文基于VS(Visual Studio)以及OpenCV(Open source Computer Vision library)開發(fā)了超聲圖像去斑應(yīng)用程序，并有良好的用戶操作界面，每幅圖像的去噪控制在很短時間以內(nèi)。在實驗中，將所提出的方法與其他幾個經(jīng)典方法進行比較，結(jié)果表明，該方法不僅具有很強的去斑能力，而且保持了圖像細節(jié)，如邊緣等，從而提高了醫(yī)學(xué)超聲圖像的質(zhì)量。

1 斑點噪聲模型和非局部平均濾波算法

1.1 斑點噪聲模型

在過去的幾年中，人們已經(jīng)提出了一些統(tǒng)計模型來描述超聲圖像中的斑點噪聲。通常認為斑點噪聲是一種乘性噪聲，并且服從瑞利分布[2]。然而，為了提高圖像的質(zhì)量，需要在輸出之前對射頻(Radio Frequency, RF)信號進行一系列的標準處理，例如非線性放大、對數(shù)壓縮、低通濾波、插值等運算，這些操作可能改變了原始信號的統(tǒng)計特性。最近的研究[7]表明，斑點噪聲近似地滿足Gamma分布或Fisher-Tippett分布。目前，最通用的斑點噪聲模型如下：

u(x)=v(x)+vγ(x)η(x)

(1)

其中：u(x)和v(x)分別代表著觀測圖像和原始圖像，η(x)～N(0,σ2)是均值為0的高斯噪聲。因數(shù)γ的值依賴于超聲裝置和圖像形成的附加處理，通常情況下，取為0.5比較適合[7]。

1.2 非局部平均濾波技術(shù)

假設(shè)一個灰度級噪聲圖像u=(u(xi))xi∈Ω定義在一個有界域Ω?R2上，u(xi)∈R+是像素點xi∈Ω的噪聲觀察灰度值。在非局部平均濾波原始的方法[25]中，每個像素xi的修復(fù)值NL(u)(xi)是通過對圖像中所有像素的灰度值加權(quán)平均得到的：

(2)

(3)

NLM濾波算法的基本思想是自然圖像中都包含有重復(fù)的結(jié)構(gòu)信息。像素與像素之間存在著相關(guān)性，而這種相關(guān)性并不局限于鄰域內(nèi)，而是涉及到整幅圖像；并且，與其他去噪方法不同，NLM算法是將圖像塊之間進行比較，而不是基于單個像素的對比。因此，它在去除高斯噪聲和保護圖像邊緣上表現(xiàn)良好，但這種方法卻不能直接應(yīng)用于去除斑點噪聲，原因在于斑點噪聲和高斯噪聲有很大不同。下面就來探討如何將非局部平均濾波器應(yīng)用于斑點噪聲的去除中。

2 基于貝葉斯NLM的超聲圖像去斑算法

2.1 貝葉斯NLM

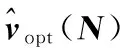
(4)

(5)

其中:p(u(N)|v(N))表示在v(N)條件下u(N)的分布。因為p(u(N)|v(N))和p(u(N))不能夠僅從圖像的一個場景中估計，換個思路，這些概率密度函數(shù)可以從圖像塊Ni的搜索窗口Δi中獲取另一個圖像塊Nj進行估計。根據(jù)文獻[24]和[28]，接下來對上式分子分母的近似值作轉(zhuǎn)變，分別如下所示：

(6)

(7)

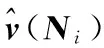
(8)

其中:p(u(Ni)|v(Nj))表示在干凈未知的圖像塊v(Nj)的條件下u(Ni)的概率密度函數(shù)。由于真實值v(Nj)是未知的，所以用觀測值u(Nj)來代替。因此，得到貝葉斯非局部平均濾波模型：

(9)

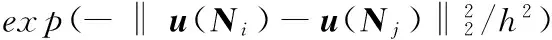
2.2 Pearson距離

基于貝葉斯NLM式(9)和斑點噪聲模型(1)，對每一個像素，有：

u(x)|v(x)～N(v(x),v(x)2γσ2)

(10)

則：

(11)

給定一個圖像塊Ni，P為該圖像塊包含的像素數(shù)目，概率計算如下(條件獨立性假設(shè)):

(12)

因此，可引出斑點噪聲干擾下圖像塊之間的距離為：

(13)

將dPearson代替式(3)中的高斯加權(quán)歐氏距離，即為適應(yīng)于斑點噪聲模型的NLM，取名PearsonNLM(Pearson Non-Local Means)。

2.3 根距離

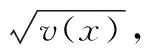
(14)

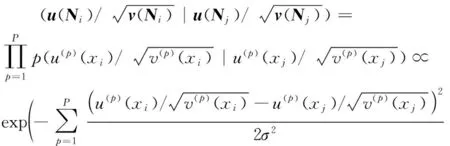
(15)

則可引出一個新的距離dsqrt用來描述受到斑點噪聲污染的圖像塊之間的差異，定義如下：

dsqrt(u(Ni),u(Nj))=

(16)

因為v是未知的，一個簡單但經(jīng)典的估計是將v替換成u，這樣最終距離公式變?yōu)椋?/p>

(17)

將dsqrt代替式(3)中的高斯加權(quán)歐氏距離，即為另一種適應(yīng)于斑點噪聲的NLM，取名SqrtNLM(Sqrt Non-Local Means)。

2.4 快速算法

NLM濾波器已經(jīng)被證明是從圖像中去除噪聲的最有效技術(shù)之一，然而，由于計算負擔的原因阻礙了它的廣泛應(yīng)用。如果待處理的圖像大小為I×I，相應(yīng)的匹配區(qū)域半徑為d，搜索區(qū)域的半徑為M，則NLM算法的整個計算復(fù)雜度將為I2×(2d+1)2×(2M+1)2。對于正在處理的每個像素，搜索區(qū)域中的所有像素都要被計算，并且相應(yīng)鄰域之間的差異也要被計算。為了加速算法，本文采用了圖像塊預(yù)選擇[29]的方法。在搜索區(qū)域Δi中對像素進行預(yù)選擇，以此避免無用權(quán)重的計算。其主要思想是在Δi中選擇權(quán)重高的像素xj，而不是使用搜索區(qū)域中的所有像素去計算距離。在本文中，使用u(Ni)和u(Nj)的平均值比值和方差比值進行預(yù)選擇，那些比值在固定范圍內(nèi)的圖像塊才用于權(quán)重計算。預(yù)選擇方式如下所示：

w(xi,xj)=

(18)

其中:μ1和σ12是兩個固定閾值，控制著最相關(guān)圖像塊的選擇。

通過這種預(yù)選擇，不僅對算法進行了加速，還能使NLM濾波器更好地保護細節(jié)區(qū)域。因為在平坦區(qū)域中，由于存在大量相似的像素，這時增加像素的數(shù)量傾向于改善去噪；與之相反，在雜亂的區(qū)域，因為有很少相似的像素，所以像素數(shù)量的增加往往會在平滑過程中消除細節(jié)。

另外，為了加速算法，本文基于VS和OpenCV對算法進行了實現(xiàn)，將處理一幅超聲斑點噪聲圖片的時間控制在很短時間之內(nèi)。在實驗中，對于所有基于NLM的方法，如果將匹配窗口和搜索窗口分別設(shè)為3×3和17×17，則PearsonNLM方法用時1.77 s，而SqrtNLM方法由于根號操作的存在時間大約31.03 s，并有良好的用戶操作界面,如圖1所示。

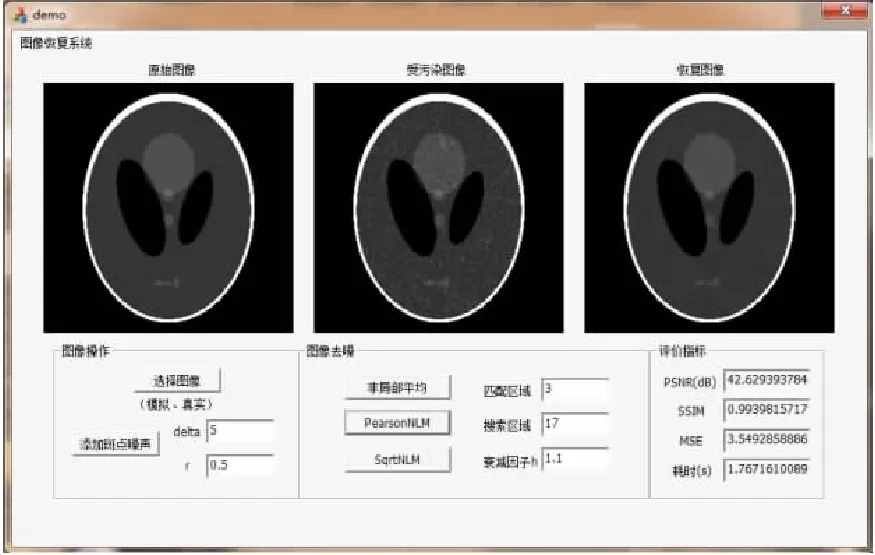
圖1 超聲圖像恢復(fù)界面 Fig. 1 Ultrasonic image recovery interface

3 實驗結(jié)果與分析

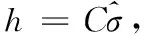
圖2 濾波參數(shù)h=Cσ對PSNR的影響 Fig. 2 Influence of smoothing parameter h=Cσ on PSNR

3.1 幻影圖像去噪實驗

在這個實驗中，幻影圖像如圖3(a)所示，它是由Matlab軟件生成的，是8位的灰度圖像，大小為256×256。斑點噪聲的模擬大致如下：首先產(chǎn)生和該圖像大小一樣的實部和虛部都是均值為0方差為σ2的復(fù)數(shù)矩陣；然后對該復(fù)數(shù)矩陣使用3×3的滑動窗口進行均值濾波；最后使用式(1)的噪聲模型對生成的幻影圖像進行加噪處理來模擬超聲圖像的斑點噪聲，這里γ取值為0.5。在污染圖像時，本文設(shè)置了四種噪聲級別σ={5,10,15,20}進行測試，對比算法的參數(shù)設(shè)置如表1所示。

為了評估去噪算法，采用兩種評價指標。一是峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)[22]值，單位dB，用式(9)來計算：

(19)

表2列出了所有評估方法的PSNR和MSSIM值，這些實驗都是在不同程度的斑點噪聲污染的幻影圖像上進行的，對應(yīng)σ=10的噪聲圖像和去噪圖像如圖3所示。從該實驗中，可以看出基于兩種新距離的NLM去噪算法在去除斑點噪聲上都有很好的表現(xiàn)，不僅在去噪圖像的PSNR值和MSSIM值上有很大的提升，同時在視覺上保留了有意義的邊緣細節(jié)。

表1 用于模擬斑點圖像的參數(shù)最佳設(shè)置Tab. 1 Optimal parameter setting for speckle image simulation

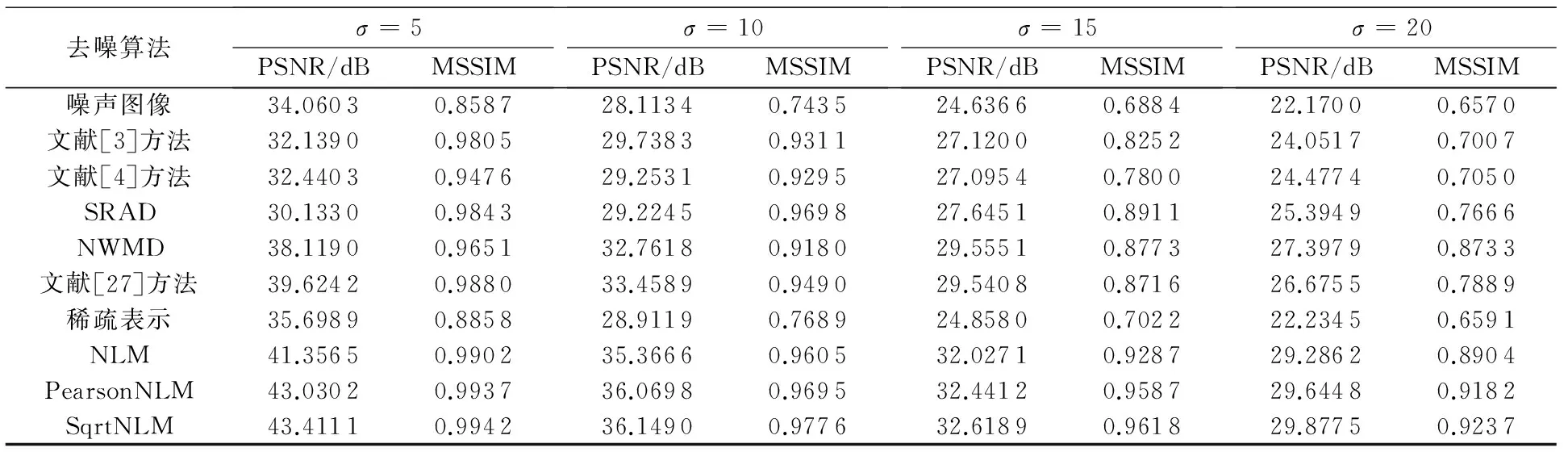
表2 γ=0.5時不同噪聲水平下的去斑方法的性能比較Tab. 2 Performance comparison for despeckling methods under different levels of noise when γ=0.5

圖3 模擬斑點圖像不同濾波器的去斑結(jié)果(σ=10) Fig. 3 Despeckling results obtained with different filters for simulated speckle image when σ=10

3.2 真實超聲圖像去噪實驗

為了評估算法對于真實超聲圖像去噪的效果，進行了如圖4和圖5所示的實驗。由于沒有任何本真圖像，因此很難用數(shù)字來評估真實超聲圖像的去斑效果。在視覺上，基于兩種新距離的NLM濾波器有效地去除了斑點成分，同時增強邊緣并保留了圖像的結(jié)構(gòu)細節(jié)。而其他的去噪方法要么斑點噪聲去除得不干凈，要么使圖片過度平滑，一些重要細節(jié)丟失,這些缺陷都不利于醫(yī)生對病情的診斷。

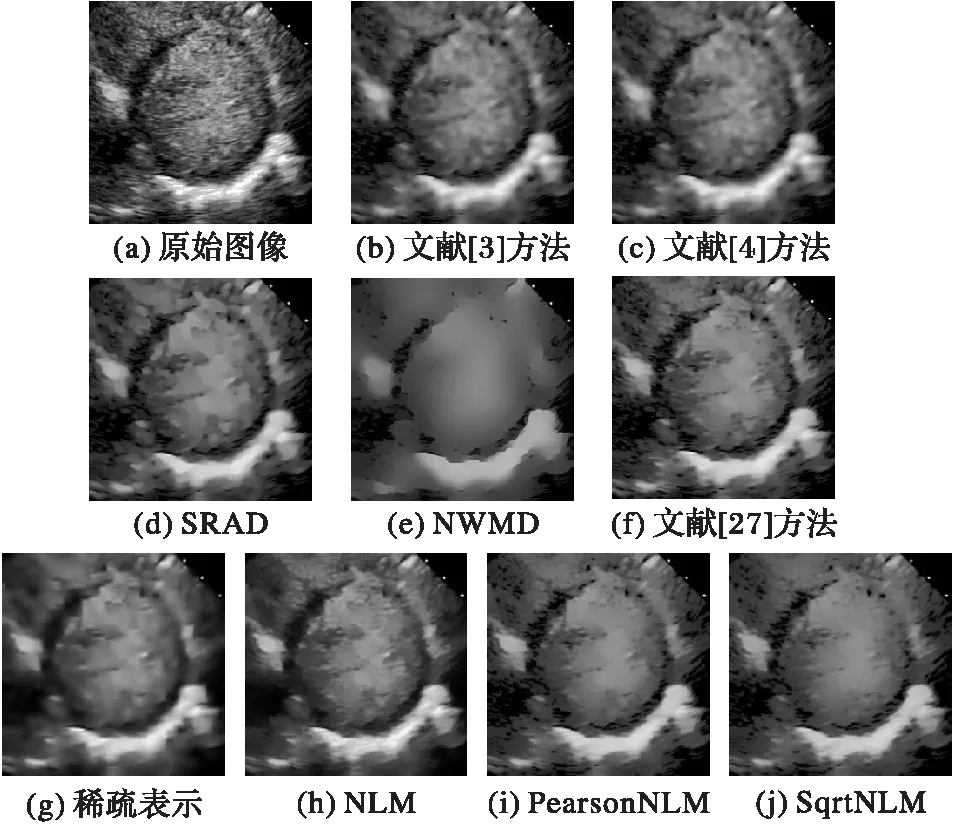
圖4 不同濾波器對體內(nèi)顯示超聲圖像的去斑結(jié)果 Fig. 4 Despeckling results obtained with different filters for in vivo displayed ultrasonic image

圖5 不同濾波器對真實超聲圖像的去斑結(jié)果 Fig. 5 Despeckling results obtained with different filters for real ultrasonic image

4 結(jié)語

在本文中，通過貝葉斯非局部平均濾波模型引入Pearson距離和根距離進行圖像塊相似度的計算，從而得到適用于濾除超聲圖像斑點噪聲的NLM濾波器。同時，本文采用了圖像塊預(yù)選擇的方案來選擇最相關(guān)的圖像塊進行權(quán)重計算，這在一定程度上提升了去噪效果。由于本文算法是在VS2013平臺下用OpenCV視覺庫實現(xiàn)的，所以算法運行的速度比在Matlab平臺下實現(xiàn)的算法快得多。為測試本文算法的去噪性能，分別在幻影圖像和真實超聲圖像上進行了實驗。實驗結(jié)果表明，相比一些現(xiàn)有的方法，基于兩種距離的NLM算法在去除斑點噪聲上都有很好的表現(xiàn)，同時保留了重要的結(jié)構(gòu)細節(jié)，這無疑有利于圖像后處理工作(如圖像配準或圖像分割)進一步得到展開。

參考文獻(References)

[1] LOIZOU C P, PATTICHIS C S, CHRISTODOULOU C I, et al. Comparative evaluation of despeckle filtering in ultrasound imaging of the carotid artery [J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2005, 52(10):1653-1669.

[2] 劉春明,張相芬,陳武凡.基于小波的醫(yī)學(xué)超聲圖像斑點噪聲抑制方法[J].中國醫(yī)學(xué)物理學(xué)雜志,2006,23(5):364-367.(LIU C M, ZHANG X F, CHEN W F. Wavelet-based method for speckle reduction in medical ultrasound image [J]. Chinese Journal of Medical Physics, 2006, 23(5): 364-367.)

[3] LEE J S. Digital image enhancement and noise filtering by use of local statistics [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1980, 2(2):165-168.

[4] FROST V S, STILES J A, SHANMUGAN K S, et al. A model for radar images and its application to adaptive digital filtering of multiplicative noise [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1982, 4(2):157-166.

[5] KUAN D T, SAWCHUK A A, STRAND T C, et al. Adaptive noise smoothing filter for images with signal-dependent noise [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1985, 7(2):165-177.

[6] 趙高長,張磊,武風波.改進的中值濾波算法在圖像去噪中的應(yīng)用[J].應(yīng)用光學(xué),2011,32(4):678-682.(ZHAO G C, ZHANG L, WU F B. Application of improved median filtering algorithm to image de-noising [J]. Journal of Applied Optics, 2011, 32(4):678-682.)

[7] 胡靜波.改進的中值濾波去噪算法分析[J].信息技術(shù),2011(8):32-33.(HU J B. Analysis of improved median filtering de-noising algorithm [J]. Information Technology,2011(8):32-33.)

[8] LOPES A, TOUZI R, NEZRY E. Adaptive speckle filters and scene heterogeneity [J]. IEEE Transactions on Geoscience and Remote Sensing,1990, 28(6): 992-1000.

[9] KARAMAN M, KUTAY M A, BOZDAGI G. An adaptive speckle suppression filter for medical ultrasonic imaging [J]. IEEE Transactions on Medical Imaging, 1995, 14(2): 283-292.

[10] PERONA P, MALIK J. Scale-space and edge detection using anisotropic diffusion [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 12(7): 629-639.

[11] RAMOS-LLORDEN G, VEGAS-SANCHEZ-FERRERO G, MARTIN-FERNANDEZ M, et al. Anisotropic diffusion filter with memory based on speckle statistics for ultrasound images [J]. IEEE Transactions on Image Processing, 2015, 24(1): 345-358.

[12] RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms [J]. Physica D: Nonlinear Phenomena, 1992, 60(1/2/3/4): 259-268.

[13] 洪志強,張立亭,陳竹安,等.基于改進的各向異性擴散圖像去噪算法研究[J].江西科學(xué),2017,35(3):433-437.(HONG Z Q, ZHANG L T, CHEN Z A, et al. Research of images denoising based on improved anisotropic diffusion algorithm [J]. Jiangxi Science, 2017, 35(3):433-437.)

[14] YU Y, MOLLOY J A, ACTON S T. Three-dimensional speckle reducing anisotropic diffusion [C]// Proceedings of the 2003 Conference Record of the 37th Asilomar Conference on Signals, Systems and Computers. Piscataway, NJ: IEEE, 2003: 1987-1991.

[15] RABBANI H, VAFADUST M, ABOLMAESUMI P, et al. Speckle noise reduction of medical ultrasound images in complex wavelet domain using mixture priors [J]. IEEE Transactions on Biomedical Engineering, 2008, 55(9): 2152-2160.

[16] NI C, LI Q, XIA L Z. A novel method of infrared image denoising and edge enhancement [J]. Signal Processing, 2008, 88(6): 1606-1614.

[17] ACHIM A, BEZERIANOS A, TSAKALIDES P. Novel Bayesian multiscale method for speckle removal in medical ultrasound images [J]. IEEE Transactions on Medical Imaging, 2001, 20(8): 772-783.

[18] KHARE A, KHARE M, JEONG Y, et al. Despeckling of medical ultrasound images using Daubechies complex wavelet transform [J]. Signal Processing, 2010, 90(2): 428-439.

[19] 趙井坤,周穎玥,林茂松.基于稀疏表示與非局部相似的圖像去噪算法[J].計算機應(yīng)用,2016,36(2):551-555.(ZHAO J K, ZHOU Y Y, LIN M S. Image denoising algorithm based on sparse representation and nonlocal similarity [J]. Journal of Computer Applications, 2016, 36(2):551-555.)

[20] HARMELING S. Image denoising: can plain neural networks compete with BM3D? [C]// Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2012: 2392-2399.

[21] 張兆倫.基于非局部均值圖像去噪算法研究[D].南京:南京郵電大學(xué),2015:19-24.(ZHANG Z L. The research on image denoising algorithm based on non-local mean [D]. Nangjing: Nangjing University of Posts and Telecommunications, 2015: 19-24.)

[22] 周穎玥,臧紅彬,趙井坤,等.基于非局部平均濾波的沖擊噪聲圖像恢復(fù)算法[J].計算機應(yīng)用研究,2016,33(11):3489-3494.(ZHOU Y Y, ZANG H B, ZHAO J K, et al. Image recovering algorithm for impulse noise based on nonlocal means filter [J]. Application Research of Computers, 2016, 33(11): 3489-3494.)

[23] SUDEEP P V, PALANISAMY P, RAJAN J, et al. Speckle reduction in medical ultrasound images using an unbiased non-local means method [J]. Biomedical Signal Processing and Control, 2016, 28(6): 1-8.

[24] KERVRANN C, BOULANGER J, COUPé P. Bayesian non-local means filter, image redundancy and adaptive dictionaries for noise removal [C]// International Conference on Scale Space and Variational Methods in Computer Vision, LNCS 4485. Berlin: Springer, 2007: 520-532.

[25] BUADES A, COLL B, MOREL J M. A review of image denoising algorithms, with a new one [J]. SIAM Journal on Multiscale Modeling and Simulation, 2010, 4(2): 490-530.

[26] BUADES A, COLL B, MOREL J. On image denoising methods [EB/OL]. [2017- 03- 12]. http://www.ece.lsu.edu/gunturk/EE7700/OnImageDenoisingMethods.pdf.

[27] COUPE P, HELLIER P, KERVRANN C, et al. Nonlocal means-based speckle filtering for ultrasound images [J]. IEEE Transactions on Image Processing, 2009, 18(10): 2221-2229.

[28] SPJ?TVOLL E. A nonlinear gaussian filter applied to images with discontinuities [J]. Journal of Nonparametric Statistics, 1997, 8(1): 21-43.

[29] MAHMOUDI M, SAPIRO G. Fast image and video denoising via nonlocal means of similar neighborhoods [J]. IEEE Signal Processing Letters, 2005, 12(12): 839-842.

This work is partially supported by the National Natural Science Foundation of China (61401379), the General Project of Educational Commission of Sichuan Province (14ZB0107).

FANGHongdao, born in 1991,M.S. candidate. His research interests include digital image processing.

ZHOUYingyue, born in 1983, Ph.D., associate research fellow. Her research interests include image processing and analysis.

LINMaosong, born in 1964, Ph.D., professor. His research interests include computer graphics and image processing, visualization in scientific computation.