結(jié)合局部灰度差異的噪聲圖像分割模型

李 鋼，李海芳，尚方信，郭 浩

(太原理工大學(xué) 計算機(jī)科學(xué)與技術(shù)學(xué)院,太原 030024)

0 引言

圖像分割在計算機(jī)視覺處理技術(shù)中占據(jù)重要位置，是圖像處理和分析的關(guān)鍵步驟。基于水平集方法的活動輪廓模型被成功應(yīng)用于在圖像分割領(lǐng)域，并取得了長足的發(fā)展，但噪聲圖像和弱邊界的分割問題，仍然具有挑戰(zhàn)性。

根據(jù)理論基礎(chǔ)不同，活動輪廓模型一般分為基于邊緣的活動輪廓模型和基于區(qū)域的活動輪廓模型。以活動測地線模型[1-5]為代表的基于邊緣的活動輪廓模型使用圖像梯度信息來引導(dǎo)活動輪廓向期望的目標(biāo)邊界運動，但該方法對圖像噪聲較為敏感，容易出現(xiàn)分割失敗的現(xiàn)象。基于區(qū)域的活動輪廓模型使用活動輪廓內(nèi)外的圖像統(tǒng)計信息的差異來引導(dǎo)分割曲線的演化，因而可以處理噪聲圖像和弱邊界圖像；該類方法可進(jìn)一步分為基于全局的活動輪廓模型和基于局部的活動輪廓模型。

全局二值擬合(Chan-Vese model, CV)模型[6]是最為著名的全局活動輪廓模型，它使用分段常數(shù)函數(shù)擬合待分割圖像灰度信息，供模型提取目標(biāo)邊緣。該方法對活動輪廓的初始位置具有魯棒性，但在處理低對比度、灰度不均勻、光照不均勻或噪聲圖像時，分段函數(shù)無法準(zhǔn)確擬合圖像，從而導(dǎo)致誤分割。Li等[7]提出的局部二值擬合(Local Binary Fitting, LBF)模型和局部圖像擬合(Local Image Fitting, LIF)模型[8]利用圖像局部灰度信息，可較準(zhǔn)確地分割灰度不均勻圖像，但上述模型對活動輪廓初始位置較為敏感，在水平集演化過程中容易陷入局部極小值，并且無法準(zhǔn)確分割噪聲圖像。

很多學(xué)者在LBF和LIF模型的基礎(chǔ)上進(jìn)行了深入研究和改進(jìn)，考慮分割子區(qū)域次序的LBF(LBF+order)方法[10]可以有效降低傳統(tǒng)LBF模型對初始輪廓位置的敏感性，全局局部融合圖像擬合(Local and Global Intensity Fitting, LGIF)模型[11]融合圖像全局信息和局部信息并提升了分割準(zhǔn)確度，但上述模型均無法有效處理圖像噪聲。一些對噪聲魯棒的方法也被相繼提出，例如：Wang等[12]在LBF的基礎(chǔ)上引入基于K-means的相關(guān)性系數(shù)得到局部K均值聚類(Local Correntropy-based K-means, LCK)模型；Jiang等[13]使用模糊C-means方法構(gòu)建局部模糊C聚類方法；Niu等[14]于2016年提出的局部相似性系數(shù)(Region-based model via Local Similarity Factor, RLSF)模型考慮了圖像局部兩點間的歐氏距離，均可實現(xiàn)對椒鹽噪聲圖像的有效分割，但上述噪聲魯棒模型均假設(shè)圖像中不包含噪聲或僅包含少量噪聲，適應(yīng)的噪聲種類范圍各有不同，在噪聲強(qiáng)度較高時會出現(xiàn)過分割或分割失敗的現(xiàn)象。

針對上述問題，本文提出一種基于像素灰度差異且在不同強(qiáng)度和種類噪聲條件下均表現(xiàn)良好的分割模型。本文提出了一種新的噪聲修復(fù)函數(shù)，其考慮了噪聲點與鄰域內(nèi)局部灰度均值間的差異，將顯著偏離鄰域均值的像素點灰度值修正至取決于圖像局部灰度均值的合理范圍內(nèi)，降低噪聲點對水平集演化的影響，提高了噪聲魯棒性和分割精度。本文認(rèn)為位于鄰域均值±2σ為合理范圍。實驗結(jié)果表明本文模型對疊加不同類型噪聲的圖像均可實現(xiàn)較為準(zhǔn)確的分割，且穩(wěn)定性較好，在不同強(qiáng)度噪聲環(huán)境下均比較理想。

1 相關(guān)理論

1.1 LCK模型

2013年，Wang等[12]提出在LBF模型的基礎(chǔ)上，引入一種基于K-means聚類方法的相關(guān)性系數(shù)，用于衡量鄰域內(nèi)像素點與鄰域中心的相似程度。該相關(guān)性系數(shù)介于0～1，某像素點處灰度值與鄰域均值相差越大，則認(rèn)為該點越可能被噪聲污染，其相似性系數(shù)越接近0。

被椒鹽噪聲污染的像素點往往與其鄰域內(nèi)灰度均值相差較大，具有較小的相關(guān)性系數(shù)，因此LCK模型的能量函數(shù)在計算中受噪聲點影響較小，對椒鹽噪聲圖像具有較好的魯棒性。LCK模型的能量函數(shù)如下所示：

(1)

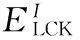
(2)

其中I為圖像灰度值。μ1、μ2為圖像內(nèi)各點附近的局部灰度均值：

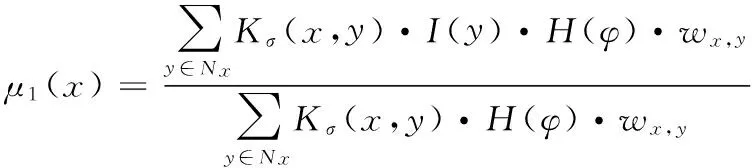
(3)

(4)

H(φ)、δ(φ)分別是規(guī)則化的Heaviside函數(shù)和Dirac函數(shù)，定義如下：

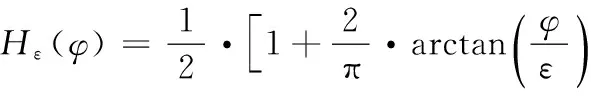
(5)

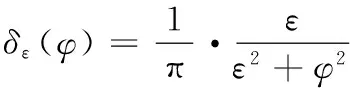
(6)

wx,y為圖像域內(nèi)x,y兩點之間的相關(guān)性系數(shù)：

wx,y=Hε(φ)·g(‖I(y)-μ1(x)‖2)+(1-Hε(φ))·g(‖I(y)-μ2(x)‖2)

(7)

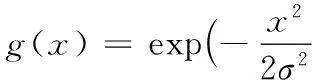
(8)

該方法通過計算圖像中各像素點的灰度值與其鄰域灰度的相關(guān)性，減少了水平集函數(shù)迭代過程中噪聲點對分割結(jié)果的影響，但由于該模型使用降低權(quán)重的思想處理噪聲點，在圖像包含較多噪聲時，可能會拋棄過多圖像內(nèi)容，出現(xiàn)分割失敗的情況。

1.2 RLSF模型

Niu等[14]于2016年提出了一種基于局部相似性系數(shù)(Local Similarity Factor, LSF)的模型，其核心思想是考慮圖像中某點x鄰域內(nèi)，除鄰域中心點x外任意一點y處灰度值與鄰域灰度均值的差異，以及點x,y之間的歐氏距離。該模型局部相似性系數(shù)形式如下：

(9)

其中:Nx是以點x為中心的鄰域范圍，lc是鄰域內(nèi)的灰度均值，d(x,y)是點x,y之間的歐氏空間距離。

RLSF模型基于局部相似性系數(shù)構(gòu)建，其泛函形式如下：

(10)

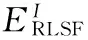
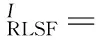
(11)

其中：M(x,y)為一個與點x,y間歐氏距離相關(guān)的距離函數(shù)，lc1、lc2分別為點x附近輪廓曲線內(nèi)外的圖像灰度均值。相關(guān)函數(shù)定義如下：

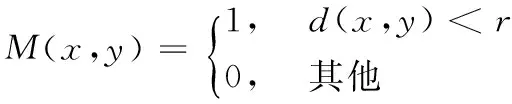
(12)

(13)

(14)

為了使水平集函數(shù)在計算過程中保持為符號距離函數(shù)，RLSF模型在Zhang等[16]和Lankton等[17]工作的基礎(chǔ)上引入了一種可變步長的迭代方法，Δt定義如下：

Δt=0.48/max(abs(φ))

(15)

基于局部相似性系數(shù)構(gòu)建的RLSF模型可以在一定范圍內(nèi)有效處理椒鹽噪聲圖像，同時對包含弱邊界或灰度不均勻圖像具有較好的適應(yīng)能力；但由于未使用高斯核函數(shù)，該方法對高斯噪聲的適應(yīng)性相對較弱。此外，該方法的迭代步長較小，與其他噪聲魯棒模型相比，完成分割需要更多次迭代。

2 噪聲自糾正的活動輪廓模型

傳統(tǒng)的噪聲魯棒模型致力于減小噪聲點對能量函數(shù)的干擾，如利用圖像全局或局部的灰度統(tǒng)計特征判定噪聲點，但在包含較高強(qiáng)度噪聲的圖像中，未被噪聲污染的像素點較少，往往會導(dǎo)致噪聲點判定方法失效，影響分割結(jié)果，出現(xiàn)過分割或誤分割。

圖1 LCK模型對噪聲像素點降權(quán)示意圖 Fig. 1 Schematic diagram of reducing noise pixel weight in LCK model

在LCK模型中，使用像素點灰度值與局部鄰域的灰度均值之間的差異，判定像素點與鄰域中心點的相關(guān)性。如圖1所示，取圖像域內(nèi)一個邊長為3的正方形鄰域，其中包含9個像素點，灰色數(shù)據(jù)柱的高度分別代表每個像素點的灰度值，點狀折線為各點權(quán)值的連線。在弱椒鹽噪聲環(huán)境下，LCK的相關(guān)性系數(shù)判定方法可以有效降低噪聲點對鄰域灰度均值的干擾。在強(qiáng)噪聲環(huán)境下，鄰域內(nèi)多個像素點均被噪聲污染，鄰域灰度均值的計算依賴于極少數(shù)接近局部灰度均值的像素點，使得大量圖像信息被棄用，并且出現(xiàn)誤分割現(xiàn)象。

本文在LCK和RLSF模型的基礎(chǔ)上，引入噪聲點修復(fù)函數(shù)R(I,f)，將大幅偏離鄰域均值的像素灰度值修復(fù)至一個合理的范圍。其能量函數(shù)構(gòu)造如下：

E(φ,f1,f2)=ERN+μ·P(φ)+ν·L(φ)

(16)

其中：P(φ)為懲罰項，用于確保水平集函數(shù)在計算過程中保持為符號距離函數(shù)，使本方法在計算過程中無需重新初始化；L(φ)為曲線長度約束項，確保分割曲線在演化過程中保持平滑。定義如下：

(17)

(18)

ERN為加入噪聲點修復(fù)函數(shù)的圖像擬合項，定義如下：

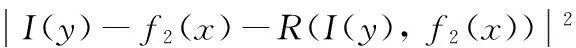
(19)

其中：λ1、λ2為權(quán)重系數(shù)，f1(x)、f2(x)分別表示點x附近輪廓線內(nèi)外的局部區(qū)域灰度值。R(I,fi)為噪聲點修復(fù)函數(shù)，由符號項、權(quán)重項和灰度項依次相乘得到，形式如下：

R(I,fi)=sign(I-fi)·(1-g(I-fi))·|I-fi|；

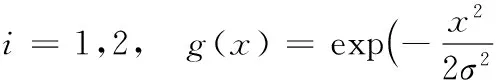
(20)

R(Ix)=min(Rin(Ix),Rout(Ix))=

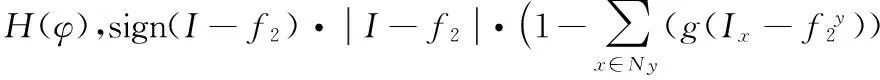
(1-H(φ))]

(21)

在計算圖像域內(nèi)各像素點的灰度修正值時，符號項保證了修正值的符號正確性，即保證噪聲點被修復(fù)至合理范圍而不是更加偏離鄰域均值；權(quán)重項介于0～1，用于限制灰度修正值不大于灰度差異值，使得修復(fù)函數(shù)在有效修正偏離均值較大的噪聲點的同時，不改變正常像素點的灰度值，確保圖像不因過度修正而丟失信息；灰度項用于衡量灰度值和鄰域均值的差異，為確定修正值提供參考依據(jù)。

由于圖像像素值和灰度均值的取值范圍均位于0～255，修正函數(shù)的取值范圍R(I,fi)∈(-255,255)。由于圖像中很少出現(xiàn)“均值趨近于0，某點像素值為255”或“均值趨近255，某點像素值為0”的情況，應(yīng)用場景下通常認(rèn)為修復(fù)函數(shù)的取值位于(-127,128)，較大的修復(fù)值不具有實際意義。

如圖2所示，灰度圖像中像素值的取值范圍為0～255，選取具有9個像素點的局部區(qū)域，局部區(qū)域灰度平均值在圖中以黑色點狀虛線表示。對于每個點y，圖中黑色實心點代表每個像素點的灰度值I(y)，黑色空心點為修正結(jié)果I(y)-R(y)，中間淺灰色區(qū)域代表修正值的跨度。以顯著偏離均值的點4為例，灰度值I=255，修正值R≈49，修正結(jié)果I(y)-R(y)=206。

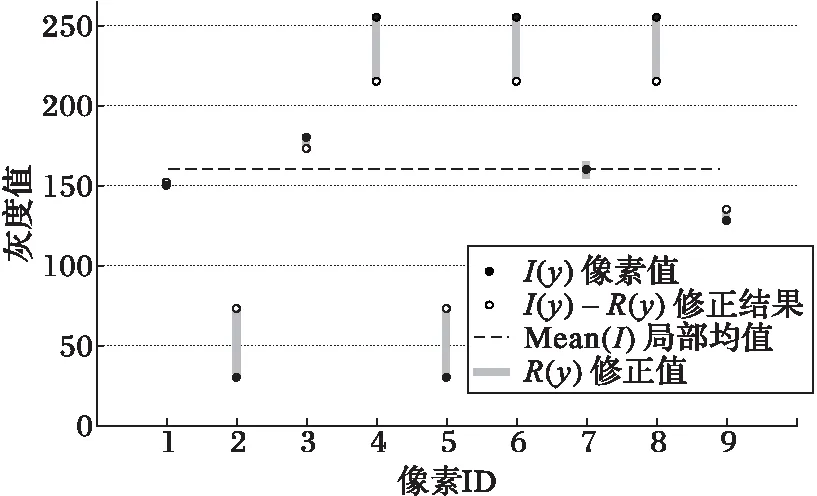
圖2 本文模型對噪聲點修正示意圖 Fig. 2 Schematic diagram of corrective effect to noise pixels in proposed model

式(19)改寫為：

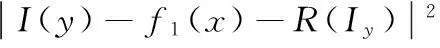
H(φ(y))dydx+λ2·?Kσ(x-y)·

(22)

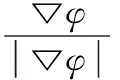
根據(jù)變分法和Euler-Lagrange方程，本文模型的水平集演化方程如下：

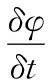
(23)

其中:

(24)

(25)

本文算法的主要步驟如下：

1)初始化二維水平集函數(shù)φ0為一與圖像大小相同的矩陣，其中心20×20像素范圍為負(fù)值(如-1)，其余為正值(如1)。將圖像分割為2類。

2)初始化R0為與圖像大小相同的零矩陣。

3)根據(jù)式(24)、(25)計算f1、f2，代表圖像域內(nèi)每一像素點在每個子區(qū)域內(nèi)的鄰域均值。

4)根據(jù)式(23)計算新的水平集函數(shù)值φi+1，取{x,y|φi+1(x,y)=0}作為新的分割輪廓。

5)根據(jù)式(20)、(21)計算Ri+1。

6)Ri=Ri+1。

7)判斷是否滿足迭代停止條件。如果滿足，停止曲線演化；否則重復(fù)步驟3)至7)。

3 實驗與結(jié)果分析

本章將給出本文模型在噪聲圖像集上的分割結(jié)果，并與LBF模型、LCK模型和RLSF模型的分割結(jié)果進(jìn)行對比。實驗結(jié)果表明本文模型在高斯噪聲和椒鹽噪聲條件下均可以保持較好的有效性和分割精度。本章實驗均在Lenovo臺式機(jī)(i3 CPU,4 GB RAM)上使用Matlab R2017a完成。操作界面如圖3所示。

圖3 實驗操作界面 Fig. 3 Experimental operation interface

如無特殊說明，本文的實驗參數(shù)設(shè)置為：λ1=1,λ2=1,μ=0.003×255×255,ν=1,Δt=0.1，ε=1。

3.1 人工合成圖像實驗

如圖4所示，本文將新模型、LCK模型和RLSF模型應(yīng)用于人工合成且疊加了椒鹽噪聲的灰度不均勻圖像的分割工作中，并對其實驗結(jié)果進(jìn)行了對比分析。其中初始輪廓由方形框線表示，分割結(jié)果由邊界處輪廓線表示。為更好地說明本文模型在噪聲環(huán)境下對期望目標(biāo)的分割性能，特將期望的分割結(jié)果體現(xiàn)于圖4第4列。其中白色區(qū)域為預(yù)期的目標(biāo)子區(qū)域，黑色區(qū)域為預(yù)期的背景子區(qū)域，邊界處輪廓線為使用本文模型得到的分割輪廓。從實驗結(jié)果可以看出，在噪聲強(qiáng)度較低時，本文模型可以準(zhǔn)確地收斂到目標(biāo)輪廓；強(qiáng)噪聲環(huán)境下，相比LCK模型、RLSF模型，本文模型具有更強(qiáng)的魯棒性。表1展示了本段實驗中LCK、RLSF和本文方法得到穩(wěn)定分割結(jié)果的用時，即從開始執(zhí)行算法到活動輪廓不再有明顯運動為止的時長。對于同一幅人工合成圖像，RLSF模型耗時最長，本文方法在強(qiáng)邊界圖像上與LCK的用時接近，在第三幅弱邊界圖像上，用時顯著短于LCK。這是由于：RLSF模型采用了較小的迭代步長，單次迭代運算量與LCK和本文方法相差不大，需要更多次迭代計算才可以達(dá)到穩(wěn)定狀態(tài)；而LCK的噪聲點降權(quán)機(jī)制使得引導(dǎo)活動輪廓向目標(biāo)邊界前進(jìn)的動力不足，活動輪廓需要更多次迭代才能達(dá)到目標(biāo)邊界；而本文模型可以高效利用原始圖像的目標(biāo)邊界信息完成分割。

圖4 不同模型噪聲環(huán)境下合成圖像的分割結(jié)果對比 Fig. 4 Segmentation results comparison on noisy synthetic images by different models 表1 不同模型在合成圖像上分割速度比較 Tab. 1 Comparison of efficiency on synthetic images

圖序分割耗時/sLCKRLSF本文方法12.88110.5712.91523.3118.1493.082312.33620.7106.608

圖5顯示了本文模型對噪聲顆粒的修正效果，第一列是疊加了強(qiáng)度為0.2的椒鹽噪聲圖像；第二列是修正圖像，即原始噪聲圖像與修復(fù)函數(shù)的差值；第三列顯示了修復(fù)函數(shù)的取值。右側(cè)色標(biāo)表示每一幅圖片對應(yīng)的修復(fù)函數(shù)R(x)取值范圍均為[-100,100]。噪聲圖像中，白色椒鹽噪聲點位置的修復(fù)函數(shù)點是白色，代表此處灰度值應(yīng)適當(dāng)降低；黑色椒鹽噪聲點位置的修復(fù)函數(shù)是黑色，代表此處灰度值應(yīng)適當(dāng)升高(減去負(fù)值)。實驗證明，本文模型針對顯著偏離鄰域均值的椒鹽噪聲點具有較強(qiáng)的糾正能力。

圖5 本文方法對噪聲像素點的糾正效果 Fig. 5 Corrective effect of proposed model on noise pixels

3.2 自然圖像實驗

為了驗證本文模型對噪聲圖像具有廣泛的適應(yīng)能力，實驗中引入Cornell大學(xué)iCoseg自然圖像數(shù)據(jù)集[19]，將圖片分辨率統(tǒng)一為128像素×128像素，并對其中每幅圖片都疊加了不同強(qiáng)度和種類的噪聲生成噪聲圖像數(shù)據(jù)集。本文在該數(shù)據(jù)集上進(jìn)行了廣泛的實驗和評估，并使用量化指標(biāo)評價各個模型的分割性能。以下選取了部分具有代表性的圖像展示實驗效果。

在椒鹽噪聲強(qiáng)度較小時，LCK模型通過相關(guān)性系數(shù)降低了噪聲點對能量泛函的影響，保證了分割的準(zhǔn)確性；RLSF模型則通過較小的迭代步長使遠(yuǎn)離初始輪廓的背景區(qū)域不會被誤分割，但是，隨著噪聲強(qiáng)度的增大，鄰域內(nèi)可供LCK參考的“正常”像素點逐漸減少，若干噪聲點都得到了較高的相關(guān)性系數(shù)，并導(dǎo)致相關(guān)性系數(shù)方法失效，出現(xiàn)較為嚴(yán)重的誤分割或分割失敗現(xiàn)象；RLSF方法在強(qiáng)椒鹽噪聲環(huán)境下迭代步長降低，不能保證分割精度，同樣會出現(xiàn)分割失敗或誤分割現(xiàn)象。本文模型在椒鹽噪聲環(huán)境下，可以使噪聲點的灰度值得到糾正，保持該點灰度特征的同時降低與鄰域內(nèi)其他像素點的差值，使得本模型在強(qiáng)噪聲環(huán)境下依然可以有效分割圖像。

如圖6所示，疊加了椒鹽噪聲的圖像使LCK、RLSF模型在背景區(qū)域更容易出現(xiàn)誤分割。這是由于被椒鹽噪聲污染的像素點與鄰域內(nèi)其他像素點反差過大，在分割輪廓演化期間被誤認(rèn)為前景區(qū)域；該噪聲點成為分割輪廓線擴(kuò)展的“種子”，在較大范圍背景區(qū)域內(nèi)引起誤分割現(xiàn)象。本文模型根據(jù)局部均值與噪聲點灰度的差異情況判別噪聲點，圖6最后一行展示了本文模型對自然圖像噪聲顆粒的修正效果，為更好地體現(xiàn)修復(fù)函數(shù)的作用，本段實驗展示將修復(fù)值從(-127,128)映射至(0,255)范圍內(nèi)。

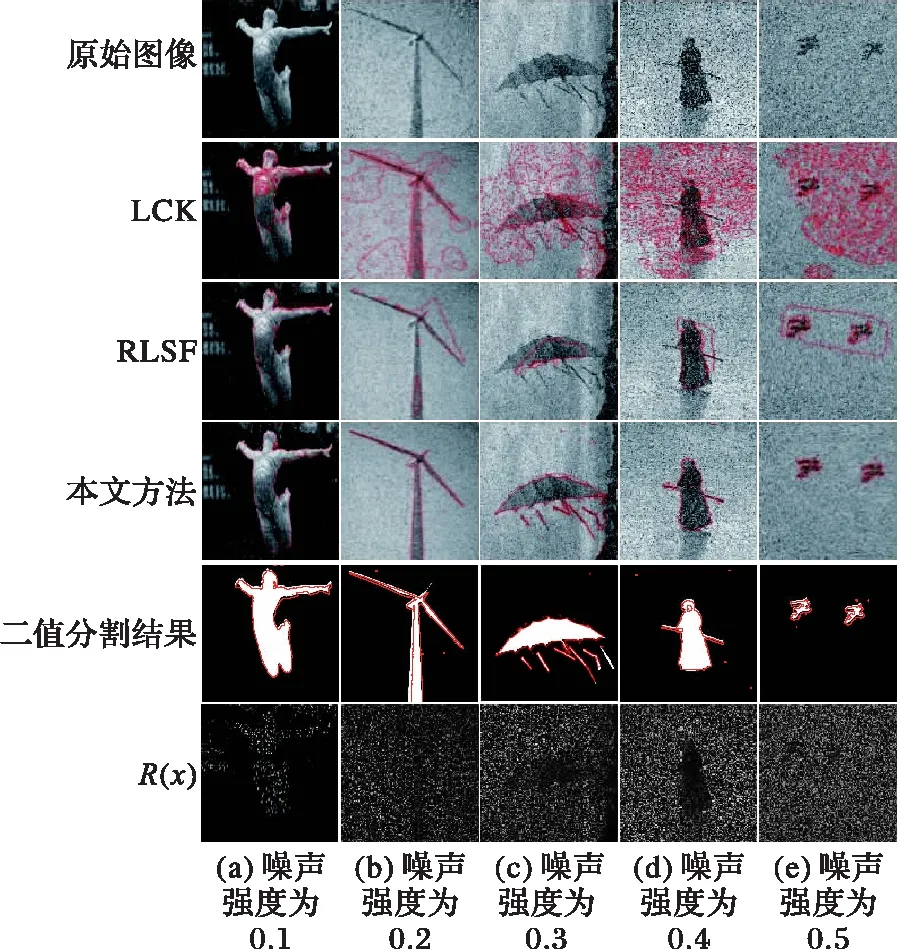
圖6 不同模型在不同椒鹽噪聲強(qiáng)度下自然圖像的分割結(jié)果對比 Fig. 6 Segmentation results on natural images with different-intensity salt and pepper noise by different models

圖7展示了本文模型、LCK、RLSF和LBF對疊加了高斯噪聲的圖像分割結(jié)果。隨著噪聲強(qiáng)度增大，所有模型均出現(xiàn)了不同程度的誤分割現(xiàn)象，且RLSF模型受到的影響更為嚴(yán)重。這是由于本文模型和LCK模型均使用高斯核函數(shù)，RLSF模型采用歐氏距離作為鄰域度量，對高斯噪聲的適應(yīng)性較差。實驗表明，在同等強(qiáng)度的高斯噪聲環(huán)境中，本文模型可獲得優(yōu)于LCK模型和RLSF模型的分割結(jié)果。這證明本文引入的噪聲點修復(fù)函數(shù)對高斯噪聲具有較好的修正能力。與椒鹽噪聲相比，高斯噪聲的極端偏離值較少，大部分集中在高斯分布的均值兩側(cè)，為更好地體現(xiàn)修復(fù)函數(shù)的作用，本段實驗將修復(fù)值從(-127,128)映射至(0,128)范圍內(nèi)。

圖7 不同模型在不同高斯噪聲強(qiáng)度下自然圖像的分割結(jié)果對比 Fig. 7 Segmentation results on natural images with different-intensity Gaussian noise by different models

表2展示了LCK、RLSF和本文方法對圖6、圖7中展示圖像的分割耗時情況，活動輪廓不再有明顯運動時終止計時。可以看出，LCK和本文方法用時接近且穩(wěn)定性較強(qiáng)，RLSF方法耗時最長且方差較大。這是由于RLSF模型采用較小的迭代步長，水平集函數(shù)在單次迭代中變化量較小，遠(yuǎn)離分割輪廓(零水平集)的區(qū)域需要更多次迭代，函數(shù)值才能接近0。因此，在相同噪聲水平下，目標(biāo)在圖像中占比越大，RLSF模型分割速度越慢。而LCK模型雖然無此缺陷，卻容易拋棄過多有價值的圖像信息，引導(dǎo)活動輪廓運動的“力量”不足，出現(xiàn)用時較長且分割失敗的情況。本文模型對噪聲類型和圖像內(nèi)容的敏感性較弱，在多種強(qiáng)度和類型的噪聲中、多種自然圖像目標(biāo)環(huán)境下，均能高效、穩(wěn)定、準(zhǔn)確地完成分割。

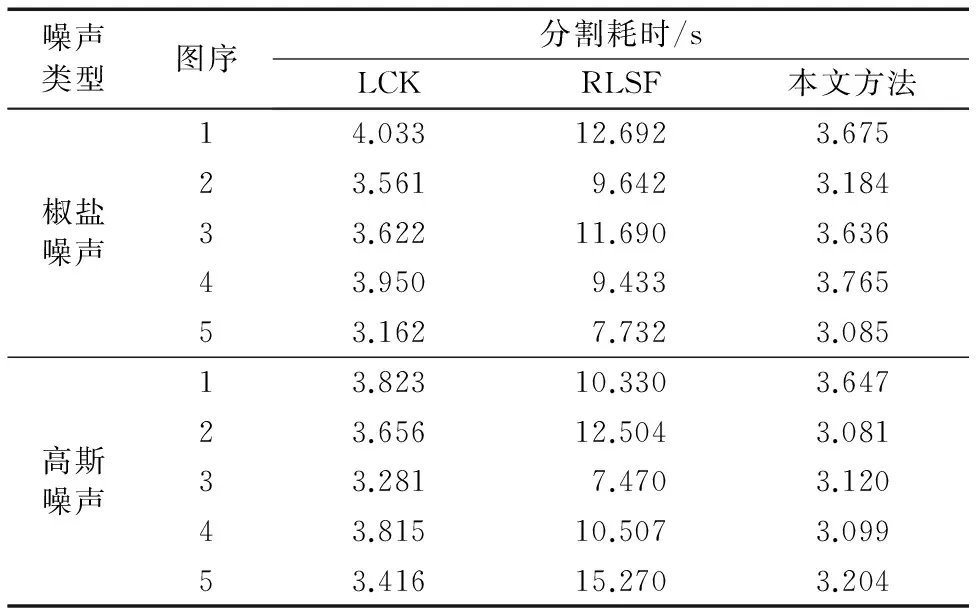
表2 不同噪聲圖像不同模型分割速度比較Tab. 2 Comparison of efficiency on natural images with different noise

為了準(zhǔn)確評估不同模型在不同噪聲條件下的分割精度，作為分割結(jié)果的水平集函數(shù)需要被二值化，即：

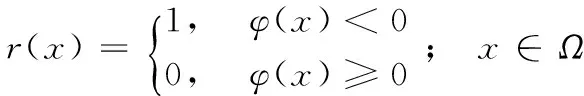
(26)

本文使用F-score作為分割精度的評估標(biāo)準(zhǔn)，其計算方式如式(27)。針對圖像中所有像素點，模型預(yù)測為目標(biāo)區(qū)域且位于參考分割結(jié)果也標(biāo)注為目標(biāo)區(qū)域的，其像素點總個數(shù)為TP；模型預(yù)測為目標(biāo)區(qū)域但參考分割結(jié)果標(biāo)注為背景區(qū)域的，其像素點總個數(shù)為FP；模型預(yù)測為背景區(qū)域但參考分割結(jié)果標(biāo)注為目標(biāo)區(qū)域的，其像素點總個數(shù)為FN；模型預(yù)測為背景區(qū)域且參考分割結(jié)果標(biāo)注為背景區(qū)域的，其像素點總個數(shù)為TN。

(27)

各個模型的分割結(jié)果越接近圖像集標(biāo)注結(jié)果，得到的F-score越高。式(27)中各參數(shù)含義如表3。

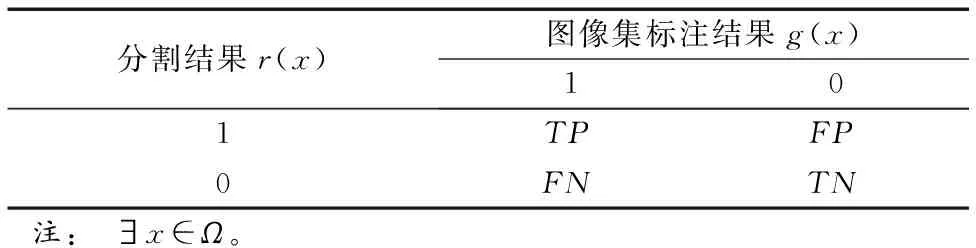
表3 計算F-score使用的參數(shù)Tab. 3 Meaning of parameters in F-score format

如圖8所示，當(dāng)測試圖像被少量椒鹽噪聲污染時，本文模型所獲得的F-score高于LCK和RLSF。

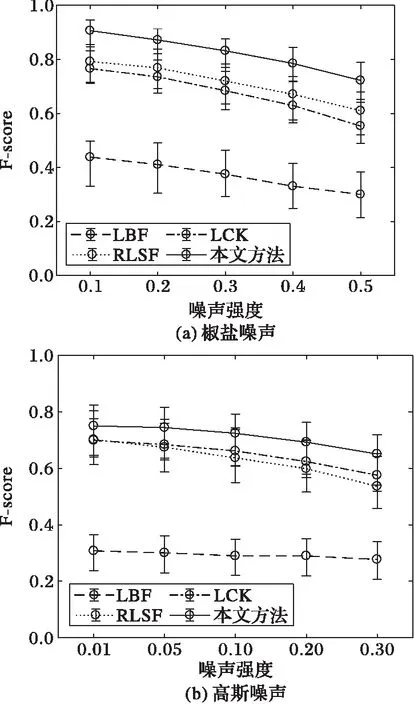
圖8 不同分割模型對不同強(qiáng)度噪聲圖像取得的F-score Fig. 8 F-score obtained by different models to natural noise images with different intensity

隨著椒鹽噪聲強(qiáng)度增加，LCK和RLSF所獲分值迅速下降，本文模型的分值下降較少。當(dāng)測試圖像被少量高斯噪聲污染時，本文模型與LCK和RLSF的分割精度接近。隨著高斯噪聲強(qiáng)度增加，3個模型的分值均呈現(xiàn)下降趨勢，但本文模型可以獲得比LCK和RLSF更高的分值，且分值差異隨著噪聲強(qiáng)度增加而變大。LBF模型對兩種噪聲的適應(yīng)性均不理想。

上述結(jié)果對比表明，本文模型在多種噪聲環(huán)境中均可以獲得優(yōu)于常見的噪聲魯棒模型的分割結(jié)果，且在椒鹽噪聲環(huán)境中表現(xiàn)出色。

4 結(jié)語

本文提出了一種基于局部灰度差異的分割模型。與LCK模型和RLSF模型相比，本文模型在多種噪聲環(huán)境下均具有較好的魯棒性，能保持良好的有效性和分割精度。LCK模型在強(qiáng)噪聲環(huán)境下拋棄了過多的圖像信息，RLSF模型僅考慮了像素點間的歐氏距離而沒有考慮高斯噪聲環(huán)境下圖像灰度值服從的分布規(guī)律。本文模型引入的噪聲點修復(fù)函數(shù)通過實時計算圖像局部灰度均值與鄰域內(nèi)每一像素點灰度值的差異，得出修正值，可以降低噪聲點對能量函數(shù)的影響，保證模型在強(qiáng)噪聲環(huán)境下仍可得到較為準(zhǔn)確的分割結(jié)果。最后，本文通過多組實驗分析并驗證了本文模型相對于其他模型在處理常見類型的噪聲圖像時的優(yōu)越性。

參考文獻(xiàn)(References)

[1] CHAPPELOW J. Snakes: active contour models[J]. International Journal of Computer Vision, 1988, 1(4): 321-331.

[2] PARAGIOS N, DERICHE R. Geodesic active regions and level set methods for supervised texture segmentation [J]. International Journal of Computer Vision, 2002, 46(3): 223-247.

[3] ZHU G, ZHANG S, ZENG Q, et al. Boundary-based image segmentation using binary level set method [J]. Optical Engineering, 2007, 46(5): 050501.

[4] XU N, AHUJA N, BANSAL R. Object segmentation using graph cuts based active contours [J]. Computer Vision and Image Understanding, 2007, 107(3): 210-224.

[5] CASELLES V, KIMMEL R, SAPIRO G. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1): 61-79.

[6] CHAN T F, VESE L A. Active contour without edges [J]. IEEE Transactions on Image Processing, 2001, 10(2):266-277.

[7] LI C, KAO C Y, GORE J C, et al. Implicit active contours driven by local binary fitting energy [C]// CVPR ’07: Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2009: 1-7.

[8] ZHANG K, SONG H, ZHANG L. Active contours driven by local image fitting energy [J]. Pattern Recognition, 2010, 43(4): 1199-1206.

[9] WANG L, MACIONE J, SUN Q, et al. Level set segmentation based on local Gaussian distribution fitting [C]// Proceedings of the 2009 Asian Conference on Computer Vision, LNCS 5994. Berlin: Springer, 2009: 293-302.

[10] WANG L F, YU Z, PAN C H. Medical image segmentation based on novel local order energy [C]// Proceedings of the 2010 Asian Conference on Computer Vision, LNCS 6493. Berlin: Springer, 2010: 148-159.

[11] JIANG X, WU X, XIONG Y, et al. Active contours driven by local and global intensity fitting energies based on local entropy [J]. Optik—International Journal for Light and Electron Optics, 2015, 126(24): 5672-5677.

[12] WANG L, PAN C. Robust level set image segmentation via a local correntropy-based K-means clustering [J]. Pattern Recognition, 2014, 47(5): 1917-1925.

[13] JIANG X L, WANG Q, HE B, et al. Robust level set image segmentation algorithm using local correntropy-based fuzzy c-means clustering with spatial constraints [J]. Neurocomputing, 2016, 207(C): 22-35.

[14] NIU S, CHEN Q, SISTERNES L D, et al. Robust noise region-based active contour model via local similarity factor for image segmentation [J]. Pattern Recognition, 2016, 61:104-119.

[15] LI C, XU C, GUI C, et al. Level set evolution without re-initialization: a new variational formulation [C]// CVPR 2005: Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2005,1: 430-436.

[16] LIE J, LYSAKER M, TAI X C. A binary level set model and some applications to Mumford-Shah image segmentation [J]. IEEE Transactions on Image Processing, 2006, 15(5):1171-1181.

[17] LANKTON S, TANNENBAUM A. Localizing region-based active contours[J]. IEEE Transactions on Image Processing, 2008, 17(11): 2029-2039.

[18] SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow [J]. Journal of Computational Physics, 1995, 114(1): 146-159.

[19] BATRA D, KOWDLE A, PARIKH D, et al. iCoseg: interactive cosegmentation by touch [DB/OL]. [2017- 05- 09]. http://chenlab.ece.cornell.edu/projects/touch-coseg/.

This work is partially supported by the National Natural Science Foundation of China (61402318).

LIGang, born in 1980, Ph. D. candidate, lecturer. His research interests include visual information processing.

LIHaifang, born in 1963, Ph. D., professor. Her research interests include computer vision, big data processing.

SHANGFangxin, born in 1990, M. S. candidate. His research interests include image processing.

GUOHao, born in 1981, Ph. D., associate professor. His research interests include intelligent information processing, artificial intelligence, brain informatics.