淮河梅山水庫流域洪水模擬不確定性分析

李彬權 梁忠民 楊曉甜 呂圣嵐 孫 浩 陳 騰

（河海大學水文水資源學院 南京 210098）

洪水預報是非工程防洪減災措施的重要組成內容，一直以來，洪水預報提供的都是一種確定性的定值預報，無法對調度方案及防洪決策的可能風險做出客觀評估。在淮河流域，隨著對洪水預報精準度、行蓄洪區調度決策和風險管理水平的要求越來越高，現有洪水預報的手段與方式難以適應新形勢下流域防洪減災和行蓄洪區調度管理的需要。水文預報不確定性分析可分為不確定性全要素耦合和預報總誤差分析兩類途徑，并形成概率預報基礎。在預報總誤差分析方面，美國貝葉斯概率預報系統BFS最具代表性。20世紀90年代，不確定性分析及概率預報概念引入國內，取得一批研究成果。

本文應用BFS中水文不確定性處理器HUP進行淮河典型流域洪水概率預報研究。通過亞高斯模型對三水源新安江模型的預報系列及實測洪水系列進行正態分位數轉化，再采用貝葉斯算法得到預報變量的后驗概率分布，實現洪水過程的概率預報。以淮河梅山水庫流域作為示例，提供了應用流程和分析結果。

1 HUP模型原理

在BFS將除具有隨機誤差以外的不確定性都歸結為水文不確定性。水文不確定性主要是由模型結構、降雨徑流計算、河道匯流和水位流量關系以及模型參數誤差等引起的。在BFS中，利用HUP模型進行水文不確定性的分析與處理。

HUP模型基本思想是概率分布的貝葉斯修正原則。待預報變量H的先驗分布需預報時事先給定，它可以根據先驗密度族｛g（·|h0）∶all h0｝來定量描述。假定河道水位（或流量）變化過程是一種馬爾可夫鏈結構，那么在觀測水位時刻 t0時給定條件 H0=h0，H 的密度函數為 g（·|h0）。

因此，水文不確定性可采用條件密度函數族｛f（·|h，y）∶all h，y｝的形式來描述，其中f（·|h，y）表示假定狀態向量為Y=y，預報變量的觀測值為H=h，且模型輸入W的預報結果是理想的（即不考慮降水輸入不確定性）條件下的模型輸出S的密度函數。對于給定的模型輸出S=s及狀態向量Y=y而言，目標函數f（s|·，y）可視為待預報變量H的似然函數。似然函數可以用來衡量系統不確定性的大小，進而反映模型預報能力的優劣。

上述g和f這兩個分布函數族可以將先驗分布的不確定性及水文不確定性傳遞至貝葉斯修正過程。給定任一預報變量h0和狀態向量y，根據全概率公式可以求得模型輸出S的期望密度函數：

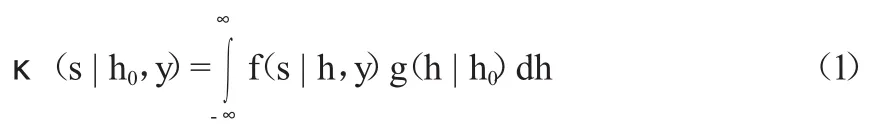
根據貝葉斯公式可以得到在給定模型輸出S=s的條件下預報變量H的后驗密度函數：

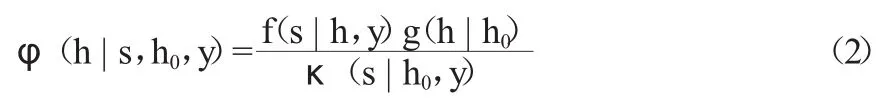
因此，預報變量H的水文不確定性可用后驗密度函數族｛φ（·|s，h0，y）∶all s，h0，y｝進行定量描述，其中處理時假定了降水輸入W沒有誤差，忽略其不確定性。

2 三水源新安江模型

新安江模型是河海大學趙人俊教授研制的國內第一個完成的流域水文模型。最初是根據霍爾頓的產流概念研制的二水源新安江模型，認為當包氣帶土壤含水量達到田間持水量后、穩定下滲量稱為地下徑流量，其余稱為地面徑流。20世紀80年代中期，借鑒山坡水文學的概念和國內外產匯流理論的研究成果，又提出了三水源新安江模型。三水源新安江模型蒸散發計算采用三層模型，產流計算采用蓄滿產流模型，用自由水蓄水庫結構將總徑流劃分為地表徑流、壤中流和地下徑流三種；流域匯流計算采用線性水庫，河道匯流采用馬斯京根分段連續演算或滯后演算法。為了考慮降水和流域下墊面分布不均勻的影響，新安江模型的結構設計為分散性的，分為蒸散發計算、產流計算、分水源計算和匯流計算四個層次結構。

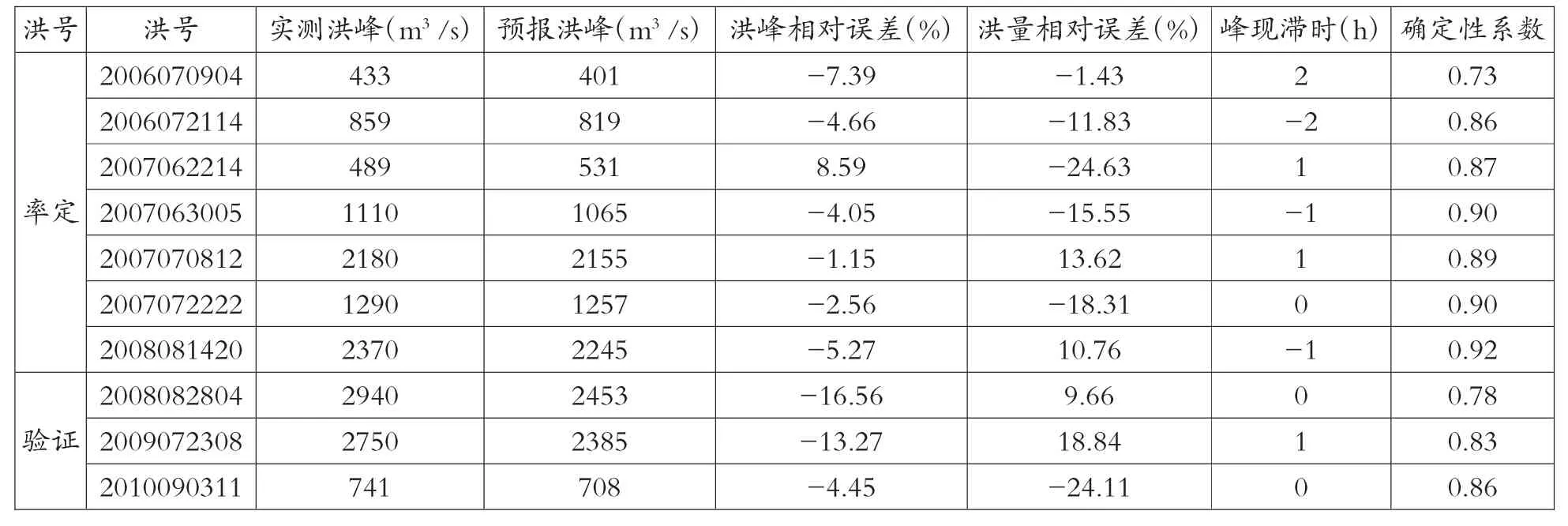
表1 梅山水庫流域次洪確定性預報結果及精度統計表

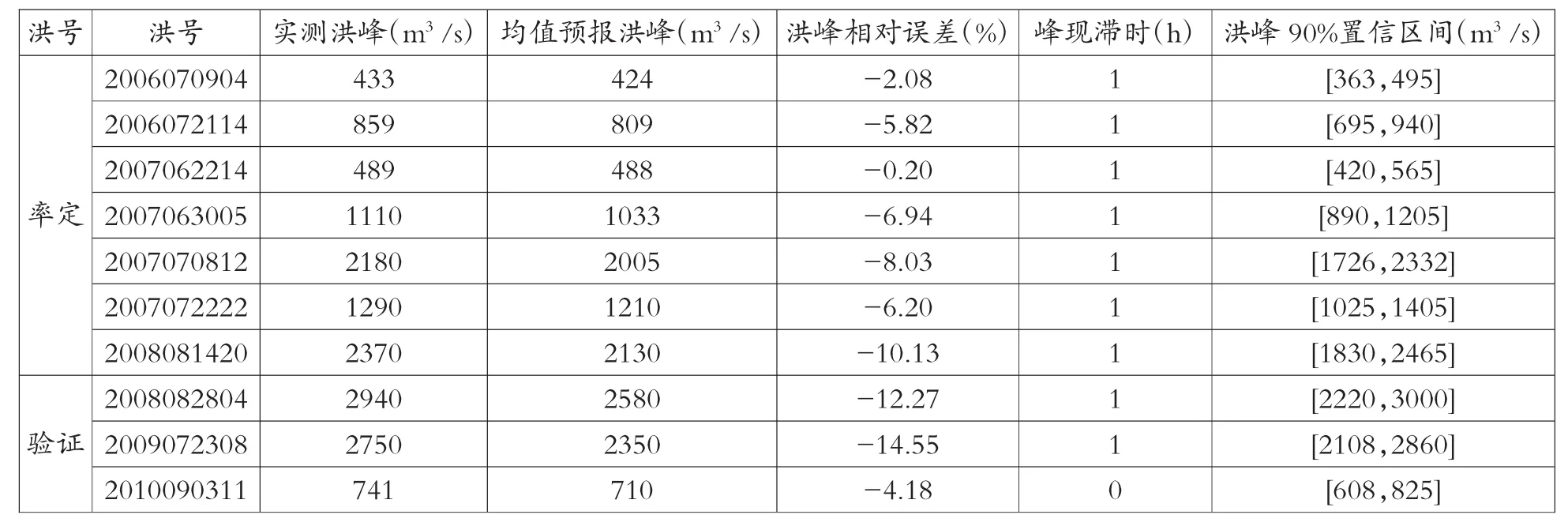
表2 梅山水庫流域次洪HUP模型概率預報的洪峰與實測值對比結果表

3 實例研究

3.1 研究流域概況

本文以淮河史灌河流域梅山水庫以上集水區域（即梅山水庫流域）作為應用驗證流域。流域面積為1970km2，地形主要以高山和丘陵為主，較為復雜，地勢呈南高北低趨勢，上游高山區坡度較陡，水流湍急，森林覆蓋率也高，而低山丘陵地帶的也有很好的植被覆蓋，壤中流和地下水十分豐富，流域產流方式為蓄滿產流。年平均徑流深738mm，多年平均降雨量為1400mm左右，雨量充沛，時空分布不均，雨量集中且多暴雨，往往形成暴漲暴落的洪水過程。

3.2 新安江模型率定與驗證

將梅山水庫流域劃分為9個子區間。其中，黃泥莊水文站所在集水區間可根據水系以及地形地貌條件將其劃分為3個子區間，七鄰水文站所在集水區間與湯匯水文站所在集水區間各為一個子區間，水庫庫區左岸的陸面同樣可根據水系及地形地貌條件劃分為兩個子區間，右岸可作為一個子區間，最后水庫庫區作為一個子區間。在每個子區間上進行新安江模型的產匯流計算，再通過河道匯流至流域出口。選用2006～2010年汛期7場次洪進行模型率定、3場次洪進行驗證，時間步長為1h，模型模擬的洪水確定性預報精度統計見表1。

由表1可知，率定和驗證次洪的確定性系數均在0.7以上，率定期和驗證期次洪模擬的平均確定性系數分別為0.87和0.82；從洪峰相對誤差來看，所有場次的洪峰相對誤差均在許可誤差20%以內，合格率達到100%；從洪量相對誤差來看，除兩場次洪的洪量相對誤差超過許可誤差的范圍，其他場次洪水的洪量相對誤差均滿足精度要求，合格率為80%；從峰現時間來看，所有場次洪水的誤差都在許可誤差（3h）以內。在新安江模型的確定性預報基礎上，可進行梅山水庫流域洪水概率預報模擬與分析。

3.3 HUP模型應用

根據HUP模型可以得到梅山水庫流域場次洪水每個時刻流量的后驗密度分布圖，進而分析得到洪水概率預報結果。表2中列出了各場洪水HUP預報結果的洪峰流量、峰現滯時及洪峰相對誤差。另外，根據HUP模型提供的實際流量的后驗密度函數，結合數理統計的原理，給定一個置信度可以計算預報流量的置信區間，表2中給出了各場洪水的HUP預報90%置信區間。結果分析表明，HUP的均值預報與實測序列擬合的較好，對次洪實測值與新安江模型預報值相差較大的洪水，由于HUP模型考慮了水文不確定性，其均值預報的洪峰誤差明顯地降低。

此外，各場洪水的大部分時段實測流量值處于概率預報結果的90%置信區間內，90%置信區間洪峰流量的上、下限在實測洪峰值的30%誤差范圍以內浮動，表明考慮水文不確定性對于洪水預報結果有顯著影響。同時對比發現，HUP預報不確定性隨著洪水量級的增大而增大。作為示例，圖1給出了第2008082804次洪水的HUP模型概率預報與新安江模型確定性預報的對比結果。

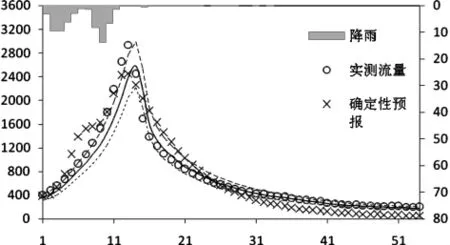
圖1 梅山水庫流域2008082804場次洪水確定性預報及概率預報過程線圖

4 小結

本文將三水源新安江模型應用于淮河史河流域的梅山水庫流域，通過具有代表性場次洪水資料的率定和驗證表明，新安江模型能夠在梅山水庫流域取得較好的模擬結果，滿足洪水精度要求，證明了新安江模型在研究流域的適用性。將水文不確定性分析模型HUP與新安江模型預報結果進行結合，分析處理了洪水預報過程中的水文不確定性，給出了均值預報結果和流量的置信區間，實現了洪水概率預報。基于HUP模型預報流量結果的置信區間信息，可以為防洪調度決策提供更為豐富的不確定性信息，使預報人員在決策中能夠定量的考慮水文不確定性，做出更為合理的決策■